7.2: Conservación de la Energía

Teorema de Poynting

Ampliamos la cantidad vectorial

\ begin {align}\ nabla\ cdot\ left (\ textbf {E}\ times\ textbf {H}\ right) & =\ textbf {H}\ cdot\ left (\ nabla\ times\ textbf {E}\ right) -\ textbf {E}\ cdot\ left (\ nabla\ times\ textbf {H}\ right)\ umber\\ & =-\ textbf {H}\ cdot\ frac {\ parcial\ textbf {B}} {\ parcial t} -\ textbf {E}\ cdot\ frac {\ parcial\ textbf {D}} {\ t parcial} -\ textbf {E}\ cdot\ textbf {J} _ {f}\ end {align}

donde cambiamos los términos de curl usando las leyes de Faraday y Ampere.

Para los medios homogéneos lineales, incluyendo el espacio libre, las leyes constitutivas son

\[ \textbf{D}=\varepsilon \textbf{E}, \quad \textbf{B}=\mu \textbf{H} \nonumber \]

para que (1) pueda ser reescrito como

\[ \nabla\cdot \left ( \textbf{E}\times \textbf{H} \right )+\frac{\partial }{\partial t}\left ( \frac{1}{2}\varepsilon \textbf{E}^{2}+\frac{1}{2}\mu \textbf{H}^{2} \right )=\textbf{E}\cdot \textbf{J}_{f} \nonumber \]

que se conoce como el teorema de Poynting. Integramos (3) sobre un volumen cerrado, utilizando el teorema de divergencia para convertir el primer término en una integral de superficie:

\[ \underbrace{\oint_{\textbf{S}}\left ( \textbf{E}\times \textbf{H} \right )\cdot \textbf{dS}}_{\int_{\textbf{V}}\nabla\cdot \left ( \textbf{E}\times \textbf{H} \right )\textbf{dV}}+\frac{d}{dt}\int_{\textbf{V}}\left (  \frac{1}{2}\varepsilon \textbf{E}^{2}+\frac{1}{2}\mu \textbf{H}^{2} \right )\textbf{dV}=-\int_{\textbf{V}}^{}\textbf{E}\cdot \textbf{J}_{f}\textbf{dV} \nonumber \]

Reconocemos que la derivada del tiempo en (4) opera sobre las densidades de energía eléctrica y magnética, lo que sugiere la interpretación de (4) como

\[ P_{out}+\frac{dW}{dt}=-P_{d} \nonumber \]

donde\(P_{out}\), es la potencia electromagnética total que fluye fuera del volumen con densidad

\[ S=\textbf{E}\times \textbf{H}\,\,\mathrm{watts/m^{2}[kg\cdot s^{-3}]} \nonumber \]

donde\(S\) se llama el vector Poynting,\(W\) es la energía electromagnética almacenada, y\(P_d\) es la potencia disipada o generada:

\[ P_{out} =\oint_{\textbf{S}}\left ( \textbf{E}\times \textbf{H} \right )\cdot \textbf{dS}=\oint_{\textbf{S}}S\cdot \textbf{dS} \\W=\int_{\textbf{V}}[\frac{1}{2}\varepsilon \textbf{E}^{2}+\frac{1}{2}\mu \textbf{H}^{2}]d\textbf{V}\\P_d=\oint_{\textbf{V}}\textbf{E}\cdot \textbf{J}_{f}d\textbf{V} \nonumber \]

Si\(\textbf{E}\) y\(\textbf{J}_{f}\) están en la misma dirección que en un conductor óhmico\(\left ( \textbf{E}\cdot \textbf{J}_{f}=\sigma E^{2} \right )\), entonces\(P_d\) es positivo, lo que representa la disipación de potencia ya que el lado derecho de (5) es negativo. Una fuente que suministra energía al volumen tiene\(\textbf{E}\) y\(\textbf{J}_{f}\) en direcciones opuestas por lo que\(P_d\) es negativa.

Un condensador con pérdida

El teorema de Poynting ofrece una explicación diferente y a algunos paradójica del flujo de potencia a los elementos del circuito. Considere el condensador cilíndrico con pérdida excitado por una fuente de voltaje variable en el tiempo en la Figura 7-1. La corriente terminal tiene contribuciones de corriente óhmica y de desplazamiento:

\[ i=\frac{\varepsilon A}{l}\frac{dv}{dt}+\frac{\sigma Av}{l}=C\frac{dv}{dt}+\frac{v}{R},\quad C=\frac{\varepsilon A}{l},\quad R=\frac{l}{\sigma A} \nonumber \]

Desde el punto de vista de la teoría de circuitos diríamos que la potencia fluye desde los cables terminales, siendo disipada en el

Figura 7-1 La potencia suministrada a un condensador cilíndrico con pérdidas\(vi\) se disipa parcialmente por la conducción óhmica y se almacena parcialmente en el campo eléctrico. También se puede pensar que este poder fluye radialmente desde los campos eléctricos y magnéticos circundantes a través del vector Poynting\(\textbf{S}=\textbf{E}\times \textbf{H}\).

resistencia y almacenada como energía eléctrica en el condensador:

\[ P=vi=\frac{v^{2}}{R}+\frac{d}{dt}(\frac{1}{2}Cv^{2}) \nonumber \]

Obtenemos los mismos resultados desde el punto de vista de un campo utilizando el teorema de Poynting. Descuidando las franjas, el campo eléctrico es simplemente

\[ E_z=v/l \nonumber \]

mientras que el campo magnético en la superficie exterior de la resistencia es generado por las corrientes de conducción y desplazamiento:

\[ \oint_{L}\textbf{H}\cdot \textbf{dl} = \int_{\textbf{S}}\left ( J_z +\varepsilon \frac{\partial E_z}{\partial t}\right )d\textbf{S}\Rightarrow H_{\phi }2\pi a=\frac{\sigma Av}{l}+\frac{\varepsilon}{l}A\frac{dv}{dt}=i \nonumber \]

donde reconocemos el lado derecho como la corriente del terminal en (8),

\[ H_{\phi }=i/\left ( 2\pi a \right ) \nonumber \]

El flujo de potencia a través de la superficie\( r = a\) que rodea la resistencia es entonces radialmente hacia adentro,

\[ \oint_{\textbf{S}}\left ( \textbf{E}\times \textbf{H} \right )\cdot \textbf{dS}= -\int_{\textbf{S}}\frac{v}{l}\frac{i}{2\pi a}a\,d\phi dz= -vi \nonumber \]

y es igual a la fórmula de potencia de circuito familiar. El signo menos surge porque el lado izquierdo de (13) es la salida de energía del volumen ya que el elemento de área de superficie\(\textbf{dS}\) apunta radialmente hacia afuera. Desde el punto de vista del campo, la energía fluye hacia el condensador con pérdidas desde los campos eléctricos y magnéticos fuera de la resistencia a través del vector Poynting. Si se piensa que la energía fluye a lo largo de los cables terminales o desde los campos circundantes es una cuestión de conveniencia ya que los resultados son idénticos. La presencia de los campos eléctrico y magnético se debe directamente a la tensión y la corriente. Es imposible tener los campos sin las variables de circuito relacionadas.

Energía en Circuitos Eléctricos

Vimos en (13) que el flujo de\(S\) entrar en la superficie que rodea a un elemento de circuito apenas es igual\(vi\). Podemos mostrar esto para la red general con\(N\) terminales en la Figura 7-2 usando las leyes de campo cuasi-estáticas que describen redes fuera de los elementos del circuito:

\ [\ nabla\ veces\ textbf {E} =0\ Rightarrow\ textbf {E} =-\ nabla V\\ nabla
\ veces\ textbf {H} =\ textbf {J} _f\ Rightarrow\ nabla\ nabla\ cdot\ textbf {J} _f=0\ nonumber\]

Luego podemos reescribir la potencia electromagnética en una superficie como

\[ \begin{align} P_{in} \nonumber & = -\oint_{\textbf{S}}\textbf{E}\times \textbf{H}\cdot \textbf{dS} \nonumber \\ &  = -\int_{\textbf{V}}\nabla\cdot \left ( \textbf{E}\times \textbf{H} \right )d\textbf{V} \nonumber \\ &  =  \int_{\textbf{V}}\nabla\cdot \left ( \nabla V\times \textbf{H} \right )d\textbf{V} \end{align} \nonumber \]

Figura 7-2 La alimentación del circuito en una red de\(N\) terminales\(\sum_{k=1}^{N} V_k I_k \) es igual al flujo de potencia electromagnética hacia la superficie que rodea la red,\(-\oint_{\textbf{S}}\textbf{E}\times \textbf{H}\cdot \textbf{dS}\).

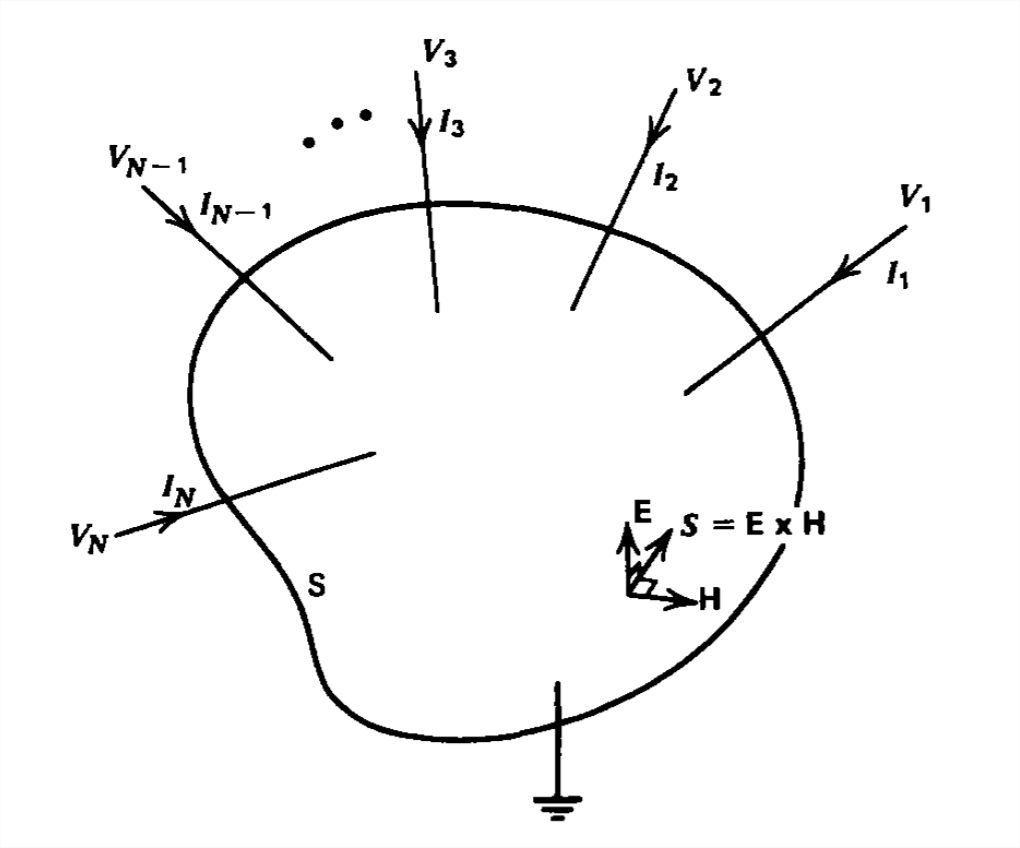
donde se introduce el signo menos porque queremos el poder y usamos el teorema de divergencia para convertir la integral de superficie en una integral de volumen. Ampliamos el término de divergencia como

\[ \begin{align} \nabla\cdot \left ( \nabla V\times \textbf{H} \right ) & =\textbf{H}\cdot \left (\overset{0}{\widehat{\nabla \times \nabla V}} \right )-\nabla V\cdot \left ( \nabla\times \textbf{H} \right ) \nonumber \\ &=-\textbf{J}_f\cdot \nabla V=-\nabla\cdot \left ( \textbf{J}_f V \right )\end{align} \nonumber \]

donde usamos (14).

Sustituyendo (16) en (15) rendimientos

\ [\ begin {align} P_ {in}\ nonumber & = -\ int_ {\ textbf {V}}\ nabla\ cdot\ left (\ textbf {J} _f V\ derecha) dV\ nonumber\\ &=\ oint_ {\ textbf {S}}\ textbf {J} _f V\ cdot\ textbf {dS}\ end {align}
\ nonumber\]

donde nuevamente usamos el teorema de la divergencia. En la superficie\(S\), el potencial solo es igual a los voltajes en cada cable terminal permitiendo\(V\) ser llevado fuera de la integral de la superficie:

\[ \begin{align} P_{in} \nonumber & = \sum_{k=1}^{N}-V_k\oint_{\textbf{S}}\textbf{J}_f\cdot \textbf{dS} \nonumber \\ &= \sum_{k=1}^{N} V_k I_k \end{align} \nonumber \]

donde reconocemos que la integral de superficie restante es solo la negativa (recuerda\(\textbf{dS}\) los puntos hacia afuera) de cada corriente terminal que fluye hacia el volumen. Esta fórmula se suele dar como postulado junto con las leyes de Kirchoff en la mayoría de los cursos de teoría de circuitos. Su corrección se deriva de las leyes de campo cuasi-estáticas que no son más que una aproximación a fenómenos más generales que seguimos explorando.

El teorema de Poynting Complejo

Para muchas situaciones los campos eléctricos y magnéticos varían sinusoidalmente con el tiempo:

\[ \textbf{E}\left ( \textbf{r},t \right )=\textbf{Re}\left [ \mathbf{\hat{E}}\left ( \textbf{r} \right )e^{j\omega t} \right ]\\ \textbf{H}\left ( \textbf{r},t \right )=\textbf{Re}\left [ \mathbf{\hat{H}}\left ( \textbf{r} \right )e^{j\omega t} \right ] \nonumber \]

donde se usa el caret para indicar una amplitud compleja que puede variar con la posición\(\textbf{r}\). La densidad de potencia instantánea se obtiene tomando el producto cruzado de\(\textbf{E}\) y\(\textbf{H}\). Sin embargo, a menudo es útil calcular la densidad de potencia promedio en el tiempo\(< \textbf{S} >\), donde podemos evitar las largas manipulaciones algebraicas y trigonométricas en la expansión de las partes reales en (19).

Se obtiene una regla simple para el promedio de tiempo de los productos al darse cuenta de que la parte real de un número complejo es igual a la mitad de la suma del número complejo y su conjugado (denotado por un asterisco superíndice). La densidad de potencia es entonces

\[ \begin{align}\textbf{S}\left ( \textbf{r}, t \right )& =\textbf{E}\left ( \textbf{r}, t \right )\times \textbf{H}\left ( \textbf{r}, t \right ) \nonumber \\ &=\frac{1}{4}\left [ \mathbf{\hat{E}}\left ( \textbf{r} \right )e^{j\omega t}+ \mathbf{\hat{E}}^{*}\left ( \textbf{r} \right )e^{-j\omega t}\right ]\times \left [ \mathbf{\hat{H}}\left ( \textbf{r} \right )e^{j\omega t}+ \mathbf{\hat{H}}^{*}\left ( \textbf{r} \right )e^{-j\omega t}\right ]\nonumber \\ &=\frac{1}{4}\left [ \mathbf{\hat{E}}\left ( \textbf{r} \right )\times  \mathbf{\hat{H}}\left ( \textbf{r} \right )e^{2j\omega t}+ \mathbf{\hat{E}}^{*}\left ( \textbf{r} \right ) \times \mathbf{\hat{H}}\left ( \textbf{r} \right )+  \mathbf{\hat{E}}\left ( \textbf{r} \right ) \times \mathbf{\hat{H}}^{*}\left ( \textbf{r} \right ) +\mathbf{\hat{E}}^{*}\left ( \textbf{r} \right ) \times \mathbf{\hat{H}}^{*}\left ( \textbf{r} \right )e^{-2j\omega t}\right ] \end{align} \nonumber \]

El promedio de tiempo de (20) es entonces

\[ \begin{align}< \textbf{S} > & =\frac{1}{4}\left [\mathbf{\hat{E}}^{*}\left ( \textbf{r} \right ) \times \mathbf{\hat{H}}\left ( \textbf{r} \right ) +\mathbf{\hat{E}}\left ( \textbf{r} \right ) \times \mathbf{\hat{H}}^{*}\left ( \textbf{r} \right )\right ] \nonumber \\ & = \frac{1}{2}\textbf{Re}\left [ \mathbf{\hat{E}}\left ( \textbf{r} \right ) \times \mathbf{\hat{H}}^{*}\left ( \textbf{r} \right ) \right ] \nonumber \\ & = \frac{1}{2}\textbf{Re}\left [ \mathbf{\hat{E}}^{*}\left ( \textbf{r} \right ) \times \mathbf{\hat{H}}\left ( \textbf{r} \right ) \right ]\end{align} \nonumber \]

como los términos exponenciales complejos\(e^{\pm 2j\omega t}\) promedian a cero durante un periodo\(T = 2\pi /\omega\) y nuevamente nos dimos cuenta de que el primer término entre corchetes en el lado derecho de (21) era la suma de una función compleja y su conjugado.

Motivados por (21) definimos el vector Poynting complejo como

\[ \mathbf{\hat{S}}=\frac{1}{2}\mathbf{\hat{E}}\left ( \textbf{r} \right ) \times \mathbf{\hat{H}}^{*}\left ( \textbf{r} \right ) \nonumber \]

cuya parte real es solo la densidad de potencia promedio en el tiempo.

Ahora podemos derivar una forma compleja del teorema de Poynting reescribiendo las ecuaciones de Maxwell para variaciones de tiempo sinusoidales como

\ [\ begin {align}
\ nabla\ times\ mathbf {\ hat {E}}\ left (\ textbf {r}\ right) &=-j\ omega\ mu\ mathbf {\ hat {H}}\ left (\ textbf {r}\ right)\ nonumber\\ nabla
\ times\ mathbf {\ hat {H}}\ left (\ tbf textbf {r}\ derecha) & =\ mathbf {\ hat {J}} _ {f}\ izquierda (\ textbf {r}\ derecha) +j\ omega\ varepsilon\ mathbf {\ hat {E}}\ left (\ textbf {r}\ derecha)\ nonumber\
\ nabla\ times\ mathbf {\ hat {E}}\ left (\ textbf {r}\ right) &=\ hat {\ rho} _ {f}\ left (\ textbf {r}\ right)/\ varepsilon\ nonumber\\
\ nabla\ veces\ mathbf {\ hat {B}}\ izquierda (\ textbf {r}\ derecha) &=0\ end {align}\ nonumber\]

y ampliar el producto

\[ \begin{align} \nabla\times \mathbf{\hat{S}} &=\nabla\cdot \left [  \frac{1}{2}\mathbf{\hat{E}}\left ( \textbf{r} \right ) \times \mathbf{\hat{H}}^{*}\left ( \textbf{r} \right )\right ]  \nonumber \\ &=\frac{1}{2}\left [ \mathbf{\hat{H}}^{*}\left ( \textbf{r} \right )\cdot \nabla\times \mathbf{\hat{E}}\left ( \textbf{r} \right ) - \mathbf{\hat{E}}\left ( \textbf{r} \right )\cdot \nabla\times \mathbf{\hat{H}}^{*}\left ( \textbf{r} \right )\right ] \nonumber \\ &=\frac{1}{2}\left [ -j\omega \mu \left | \mathbf{\hat{H}}\left ( \textbf{r} \right ) \right |^{2} +j\omega \varepsilon \left | \mathbf{\hat{E}}\left ( \textbf{r} \right ) \right |^{2}-\frac{1}{2}\mathbf{\hat{E}}\left ( \textbf{r} \right )\cdot \mathbf{\hat{J}}_{f}^{*}\left ( \textbf{r} \right )\right ] \end{align} \nonumber \]

que se puede reescribir como

\[\nabla\times \mathbf{\hat{S}} +2j\omega \left [ < \omega _{m}> -< \omega_{e} >  \right ]=-\hat{P}_{d} \nonumber \]

donde

\ [\ begin {align}
<\ omega _ {m} > &=\ frac {1} {4}\ mu\ left |\ mathbf {\ hat {H}}\ left (\ textbf {r}\ right)\ right |^ {2}\ nonumber\\
<\ omega_ {e} > &=\ frac {1} {4}\ varepsilon\ left |\ mathbf {\ hat {E}\ left (\ tbf {r}\ derecha)\ derecha |^ {2}\ nonumber\
\ sombrero {P} _ _ {d} & =\ frac {1} {2}\ mathbf {\ hat {E}}\ izquierda (\ textbf {r}\ derecha)\ cdot\ mathbf {\ hat {J}} _ {f} ^ {*}\ izquierda (\ textbf {r}\ derecha)\ end {align}\ nonumber\]

Observamos que\(< \omega _{m}\) y\(< \omega_{e} >\) son las densidades de energía magnética y eléctrica promedio en el tiempo y que el teorema complejo de Poynting depende de su diferencia más que de su suma.