7.3: Ondas Electromagnéticas Transversales

Ondas Planas

Tratemos de encontrar soluciones a las ecuaciones de Maxwell que sólo dependen de la\(z\) coordenada y el tiempo en medios lineales con permitividad\(\varepsilon\) y permeabilidad\(\mu\). En regiones donde no hay fuentes para que\(\rho _{f}=0\),\(\textbf{J}_{f}=0\), las ecuaciones de Maxwell luego se reduzcan a

\[-\frac{\partial E_{y}}{\partial z}\textbf{i}_{x}+\frac{\partial E_{x}}{\partial z}\textbf{i}_{y}=-\mu \frac{\partial \textbf{H}}{\partial t} \nonumber \]

\[ -\frac{\partial H_{y}}{\partial z}\textbf{i}_{x}+\frac{\partial H_{x}}{\partial z}\textbf{i}_{y}=\varepsilon  \frac{\partial \textbf{E}}{\partial t} \nonumber \]

\[ \varepsilon \frac{\partial E_{z}}{\partial z}=0 \nonumber \]

\[\mu \frac{\partial H_{z}}{\partial z}=0 \nonumber \]

Estas relaciones nos dicen que en el mejor de los casos\(E_{z}\), y\(H_{z}\), son constantes en el tiempo y en el espacio. Debido a que están desacopladas, a falta de fuentes las tomamos como cero. Al separar los componentes del vector en (1) y (2) vemos que\(E_{x}\) se acopla a\(H_{y}\), y\(E_{y}\), se acopla a\(H_{x}\):

\[ \frac{\partial E_{x}}{\partial z}=-\mu \frac{\partial H_{y}}{\partial t}, \quad \frac{\partial E_{y}}{\partial z}=\mu\frac{\partial H_{x}}{\partial t}\\ \frac{\partial H_{y}}{\partial z}=-\varepsilon \frac{\partial E_{x}}{\partial t}, \quad \frac{\partial H_{x}}{\partial z}=\varepsilon \frac{\partial E_{y}}{\partial t}  \nonumber \]

formando dos conjuntos de ecuaciones independientes. Cada solución tiene campos eléctricos y magnéticos perpendiculares. El flujo de potencia\(\textbf{S}=\textbf{E}\times \textbf{H}\) para cada solución se\(z\) dirige también siendo perpendicular a\(\textbf{E}\) y\(\textbf{H}\). Dado que los campos y el flujo de potencia son mutuamente perpendiculares, tales soluciones se denominan ondas electromagnéticas transversales (TEM). Son ondas porque si tomamos\(\partial/\partial z\) de las ecuaciones superiores y\(\partial/\partial t\) de las ecuaciones inferiores y resolvemos para los campos eléctricos, obtenemos ecuaciones de onda unidimensionales:

\[ \frac{\partial^2 E_{x}}{\partial z^2}=\frac{1}{c^{2}}\frac{\partial^2 E_{x}}{\partial t^2},\quad \frac{\partial^2 E_{y}}{\partial z^2}=\frac{1}{c^{2}}\frac{\partial^2 E_{y}}{\partial t^2} \nonumber \]

donde\(c\) esta la velocidad de la ola,

\[ c=\frac{1}{\sqrt{\varepsilon \mu }}=\frac{1}{\sqrt{\varepsilon _{0}\mu _{0}}\sqrt{\varepsilon _{r}\mu _{r}}}\approx \frac{3\times 10^{8}}{\sqrt{\varepsilon _{r}\mu _{r}}}\,\mathrm{m/sec} \nonumber \]

En el espacio libre, donde\(\varepsilon _{r}=1\) y\(\mu _{r}=1\), esta cantidad equivale a la velocidad de la luz en vacío lo que demostró que la luz es una onda electromagnética transversal. Si tomamos\(\partial/\partial t\) de manera similar las ecuaciones superior e\(\partial/\partial z\) inferior en (5), obtenemos ecuaciones de onda en los campos magnéticos:

\[ \frac{\partial^2 H_{y}}{\partial z^2}=\frac{1}{c^{2}}\frac{\partial^2 H_{y}}{\partial t^2},\quad \frac{\partial^2 H_{x}}{\partial z^2}=\frac{1}{c^{2}}\frac{\partial^2 H_{x}}{\partial t^2} \nonumber \]

La Ecuación de Onda

a) Soluciones

Estas ecuaciones surgen en muchos sistemas físicos, por lo que sus soluciones son bien conocidas. Trabajando con las ecuaciones\(\) E y\(\) H, las soluciones son

\ [E_ {x}\ izquierda (z, t\ derecha) =E_ {+}\ izquierda (t-z/c\ derecha) +E_ {-}\ izquierda (t+z/c\ derecha)\
H_ {y}\ izquierda (z, t\ derecha) =H_ {+}\ izquierda (t-z/c\ derecha) +H_ {-}\ izquierda (t+z/c\ derecha)\ nonumber\]

donde las funciones\(E_{+}\),,\(E_{-}\)\(H_{+}\), y\(H_{-}\) dependen de las condiciones iniciales en el tiempo y las condiciones de límite en el espacio. Estas soluciones se pueden verificar fácilmente definiendo los argumentos\(\alpha\) y\(\beta \) con sus derivadas parciales resultantes como

\[ \alpha = t-\frac{z}{c}\Rightarrow \frac{\partial \alpha }{\partial t}=1,\quad \frac{\partial \alpha }{\partial z}=-\frac{1}{c}\\\beta =t+\frac{z}{c}\Rightarrow \frac{\partial \beta }{\partial t} =1,\quad \frac{\partial \beta }{\partial z}=\frac{1}{c} \nonumber \]

y darse cuenta de que las primeras derivadas parciales de\(E_{x}\left ( z,t \right )\) son

\ [\ begin {align}\ frac {\ parcial E_ {x}} {\ parcial t} & =\ frac {\ mathrm {d} E_ {+}} {\ mathrm {d}\ alpha}\ frac {\ parcial\ alfa} {\ parcial t} +\ frac {\ mathrm {d} E_ {-}} {\ mathrm {d}\ beta} frac {\ parcial\ beta} {\ t parcial}\ nonumber\\ & =\ frac {\ mathrm {d} E_ {+}} {\ mathrm {d}\ alpha} +\ frac {\ mathrm {d} E_ {-}} {\ mathrm {d} \ beta}\ nonumber\
\ frac {\ parcial E_ {x}} {\ z parcial} & =\ frac {\ mathrm {d} E_ {+}} {\ mathrm {d}\ alpha}\ frac {\ parcial\ alpha} {\ parcial\ alpha} {\ parcial z} +\ frac {\ mathrm {d} E_ {-}} {\ mathrm {d} beta\}\ frac {\ parcial\ beta} {\ z parcial}\ nonumber\\ & =\ frac {1} {c}\ izquierda (-\ frac {\ mathrm {d} E_ {+}} {\ mathrm {d}\ alpha } +\ frac {\ mathrm {d} E_ {-}} {\ mathrm {d}\ beta}\ derecha)\ end {align}\ nonumber\]

Los segundos derivados son entonces

\ [\ begin {align}\ frac {\ parcial^2 E_ {x}} {\ parcial t^2} & =\ frac {\ mathrm {d} ^2 E_ {+}} {\ mathrm {d}\ alpha ^2}\ frac {\ parcial\ alfa} {\ t parcial} +\ frac {\ mathrm {d} ^2 E_ {-} {\ mathrm {d}\ beta^2}\ frac {\ parcial\ beta} {\ parcial t}\ nonumber\\ & =\ frac {\ mathrm {d} ^2 E_ {+}} {\ mathrm {d}\ alpha^2} +\ frac {\ mathrm {d} ^2 E_ {-}} {\ mathrm {d}\ beta^2}\ nonumber\
\ frac {\ parcial^2 E_ {x}} {\ parcial z^2} & =\ frac {1} {c}\ izquierda (-\ frac {\ mathrm {d} ^2 E_ {+}} {\ mathrm {d}\ alpha^2}\ frac ac {\ parcial\ alfa} {\ z parcial} +\ frac {\ mathrm {d} ^2 E_ {-}} {\ mathrm {d}\ beta^2}\ frac {\ parcial\ beta} {\ z parcial}\ derecha)\ nonumber\\ & = \ frac {1} {c^2}\ left (-\ frac {\ mathrm {d} ^2 E_ {+}} {\ mathrm {d}\ alpha^2} +\ frac {\ mathrm {d} ^2 E_ {-}} {\ mathrm {d}\ beta^2}\ derecha) =\ frac {1} {c^2}\ frac {1} {c^2}\ frac ac {\ parcial^2 E_ {x}} {\ parcial t^2}\ end {align}\ nonumber\]

que satisface la ecuación de onda de (6). Operaciones similares aplican para\(H_{y}\),\(E_{y}\), y\(H_{x}\).

En (9), el par\(H_{+}\) y así\(E_{+}\) como el par\(H_{-}\) y no\(E_{-}\) son independientes, como puede verse sustituyendo las soluciones de (9) de nuevo en (5) y usando (11):

\[ \frac{\partial E_{x}}{\partial z}= -\mu \frac{\partial H_{y}}{\partial t}\Rightarrow \frac{1}{c}\left ( -\frac{\mathrm{d} E_{+}}{\mathrm{d} \alpha }+\frac{\mathrm{d} E_{-}}{\mathrm{d} \beta } \right )=-\mu \left ( \frac{\mathrm{d} H_{+}}{\mathrm{d} \alpha }+\frac{\mathrm{d} H_{-}}{\mathrm{d} \beta } \right ) \nonumber \]

Las funciones de\(\alpha\) y\(\beta\) deben ser por separado iguales,

\[ \frac{\mathrm{d} }{\mathrm{d} \alpha }\left ( E_{+}-\mu cH_{+} \right )=0, \quad \frac{\mathrm{d} }{\mathrm{d} \beta }\left ( E_{-}+\mu c H_{-} \right )=0 \nonumber \]

lo que requiere que

\[ E_{+}=\mu c H_{+}=\sqrt{\frac{\mu }{\varepsilon }H_{+}},\quad E_{-}=-\mu cH_{-}=-\sqrt{\frac{\mu }{\varepsilon }H_{-}} \nonumber \]

donde usamos (7). Ya que\(\sqrt{\mu /\varepsilon }\) tiene unidades de Ohmios, esta cantidad se conoce como la impedancia de onda\(\eta \),

\[ \eta =\sqrt{\frac{\mu }{\varepsilon }}\approx 120\pi \sqrt{\frac{\mu _{r}}{\varepsilon _{r}}} \nonumber \]

y tiene valor\(120\pi \approx 377\) ohm en espacio libre\(\left ( \mu _{r}=1,\varepsilon _{r}=1 \right )\).

La densidad de flujo de potencia en las ondas TEM es

\[\begin{align} \textbf{S} =\textbf{E}\times \textbf{H} & =\left [ E_{+}\left ( t-z/c \right )+E_{-}\left ( t+z/c \right ) \right ]\textbf{i}_{x}\times \left [ H_{+}\left ( t-z/c \right )+H_{-}\left ( t+z/c \right ) \right ]\textbf{i}_{y} \nonumber \\ & =\left ( E_{+}H_{+}+E_{-}H_{-}+E_{-}H_{+}+E_{+}H_{-} \right )\textbf{i}_{z} \end{align} \nonumber \]

Usando (15) y (16) este resultado puede escribirse como

\[ S_{z}=\frac{1}{\eta }\left ( E_{+}^{2}-E_{-}^{2} \right ) \nonumber \]

donde los dos últimos términos cruzados en (17) cancelan debido al signo menos relativo\(E_{-}\) a\(H_{-}\) en (15). Para las ondas TEM, la densidad de flujo de potencia total se debe a la diferencia en las densidades de potencia entre los cuadrados de las ondas\(z\) dirigidas positivamente y las\(z\) dirigidas negativamente.

b) Inmuebles

Las soluciones de (9) son la propagación de ondas a velocidad\(c\). Para ver esto, examinemos\(E_{+}\left ( t-z/c \right )\) y consideremos el caso donde at\(z = 0\),\(E_{+}(t)\) es el pulso de escalera que se muestra en la Figura 7-3a. En la Figura 7-3b sustituimos el argumento\(t\) por\(t-z/c\). Siempre y cuando la función\(E_{+}\) esté trazada versus su argumento, no importa cuál sea su argumento, la trama permanece sin cambios. Sin embargo, en la Figura 7-3c\(E_{+}\left ( t-z/c \right )\) se grafica la función versus\(t\) dando como resultado que el pulso se traduzca en el tiempo en una cantidad\(z/c\). Para ayudar a trazar esta función traducida, utilizamos la siguiente lógica:

1. El pulso salta a amplitud\(E_{0}\) cuando el argumento es cero. Cuando el argumento es\(t -z/c\), esto ocurre para\(t = z/c\).
2. El pulso salta a amplitud\(2E_{0}\) cuando el argumento es\(T\). Cuando el argumento es\(t -z/c\), esto ocurre para\(t= T +z/c\).
3. El pulso vuelve a cero cuando el argumento es\(2T\). Para el argumento\(t -z/c\), tenemos\(t =2 T+z/c\).

La figura 7-3 (a)\(E_{+}(t)\) at\(z =0\) es un pulso de escalera. (b)\(E_{+}\left ( \phi  \right )\) siempre tiene la misma forma que (a) cuando se traza versus\(\phi\), no importa lo que\(\phi\) sea. Aquí\(\phi =t -z/c\). (c) Cuando se grafica versus\(t\), el pulso se traduce en tiempo donde\(z\) debe ser positivo para mantenerse\(t\) positivo. d) Cuando se traza versus\(z\), se traduce e invierte. El pulso se propaga a velocidad\(c\) en la\(z\) dirección positiva.

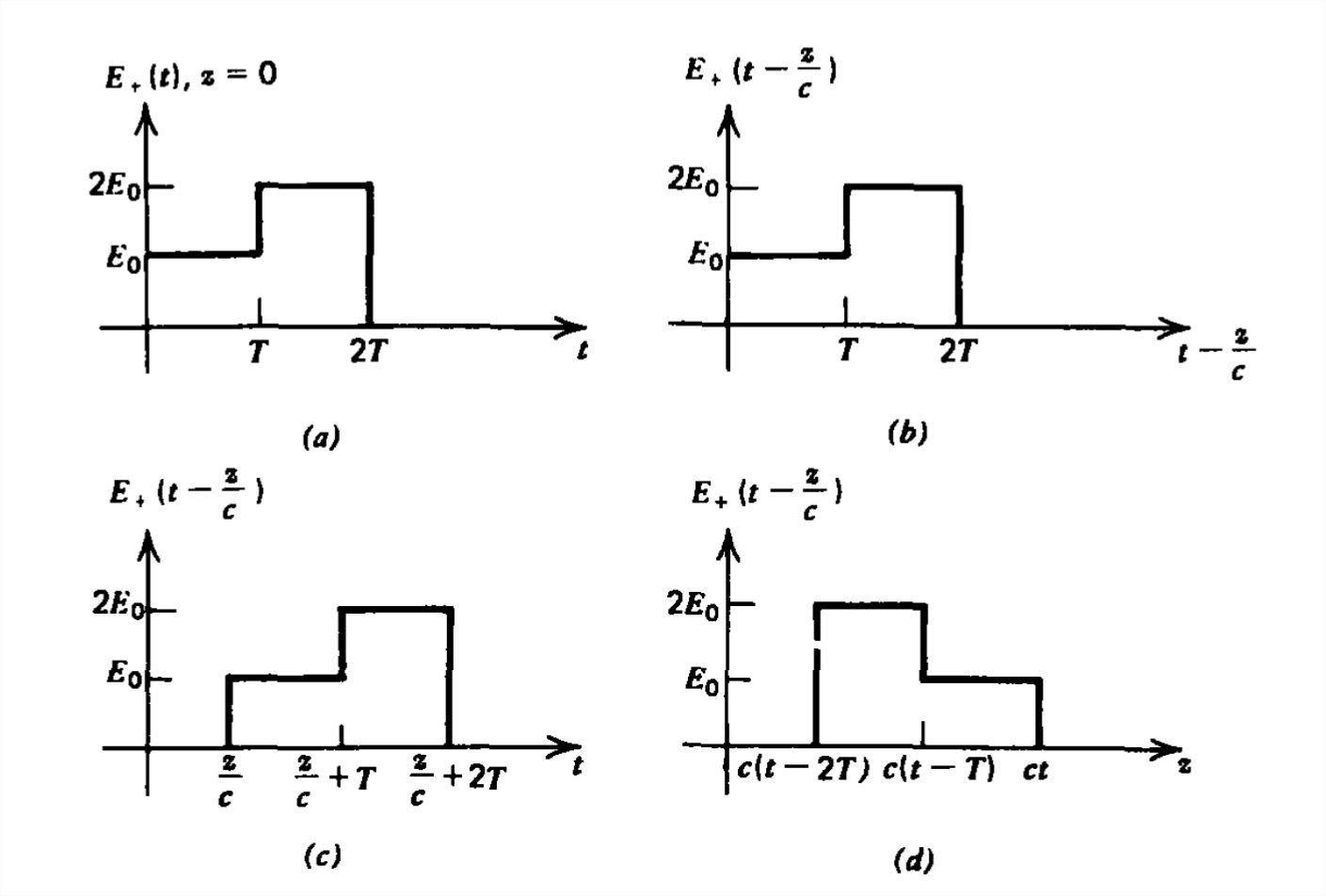
Tenga en cuenta que sólo\(z\) puede ser positivo ya que la causalidad impone la condición de que el tiempo sólo puede estar aumentando. La respuesta en cualquier posición positiva\(z\) a un pulso inicial\(E_{+}\) impuesto en\(z = 0\) tiene la misma forma en el tiempo pero ocurre en un momento\(z/c\) posterior. El pulso recorre la distancia\(z\) a la velocidad\(c\). Es por ello que a la función\(E_{+}(t -z/c)\) se le llama onda positiva que viaja.

En la Figura 7-3d trazamos la misma función versus\(z\). Su apariencia se invierte ya que esa parte del pulso generado primero (paso de amplitud\(E_{0}\)) alcanzará cualquier posición positiva\(z\) primero. El segundo paso de amplitud no\(2E_{0}\) ha viajado tan lejos desde que se generó un tiempo\(T\) después. Para ayudar en el trazado, utilizamos el mismo criterio en el argumento que se usa en la trama versus tiempo, solo que resolvemos para\(z\). La regla importante que utilizamos es que mientras el argumento de una función permanezca constante, el valor de la función no cambia, sin importar cómo cambien los términos individuales en el argumento.

Por lo tanto, siempre y cuando

\[ t -z/c= \mathrm{const} \nonumber \]

\(E_{+}(t -z/c)\)no ha cambiado. A medida que aumenta el tiempo, también debe\(z\) satisfacer (19) a la tasa

\[ t-\frac{z}{c}=\mathrm{const}\Rightarrow \frac{\mathrm{d} z}{\mathrm{d} t}=-c \nonumber \]

para mantener la\(E_{+}\), función constante.

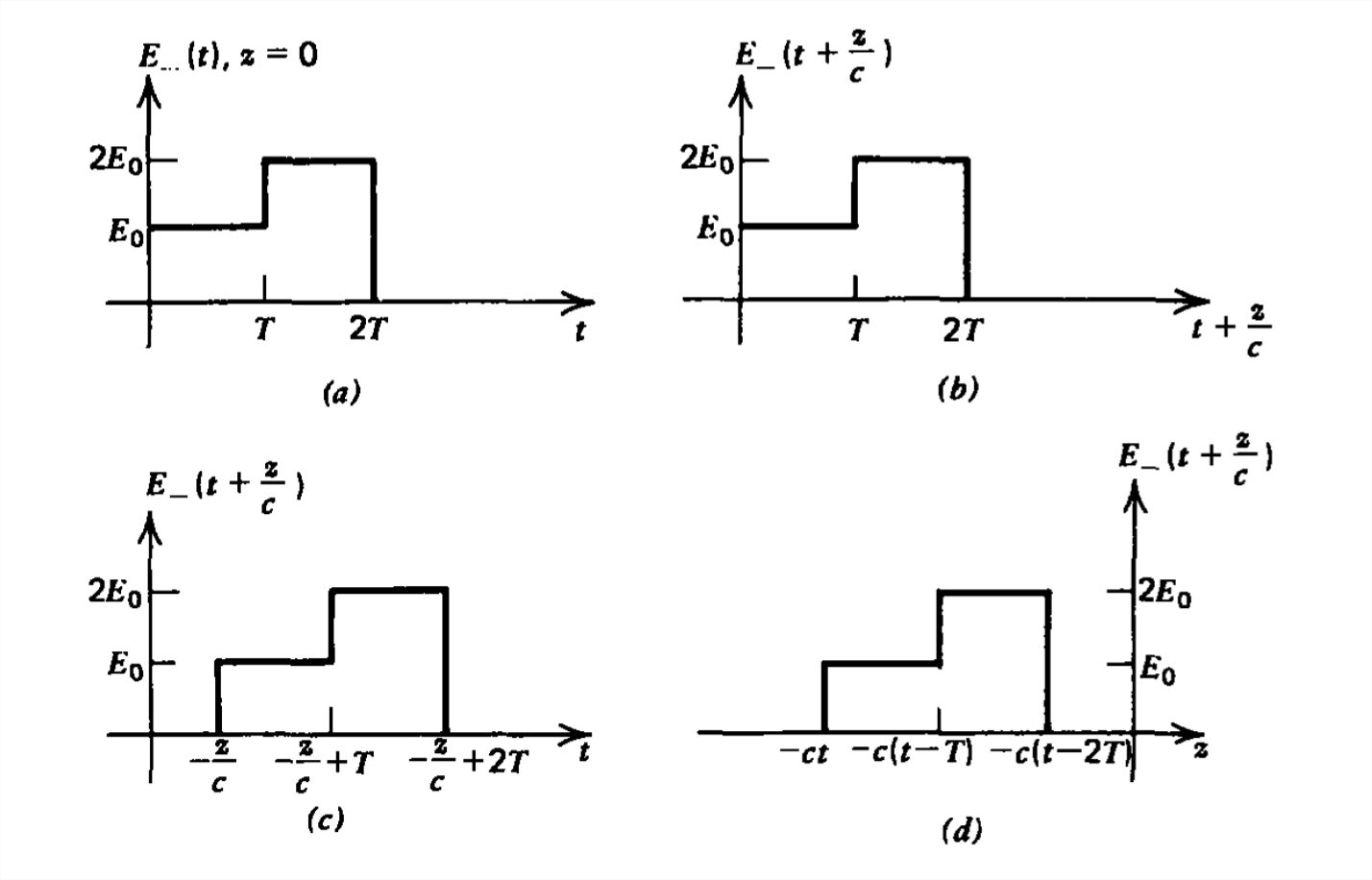
Por razones similares\(E_{+}(t +z/c)\) representa una onda viajera a la velocidad\(c\) en la\(z\) dirección negativa ya que un observador debe moverse para mantener el argumento\(t +z/c\) constante a velocidad:

\[ t+\frac{z}{c}=\mathrm{const}\Rightarrow \frac{\mathrm{d} z}{\mathrm{d} t}=c \nonumber \]

como se demostró para el mismo pulso de escalera en la Figura 7-4. Obsérvese en la Figura 7-4d que el pulso no se invierte cuando se grafica versus\(z\) como lo fue para la onda que viaja positivamente, porque esa parte del pulso generado primero (paso de amplitud\(E_{0}\)) alcanza la distancia máxima pero en la\(z\) dirección negativa. Estas diferencias entre las olas que viajan positiva y negativamente se deben funcionalmente a la diferencia de signos en los argumentos\((t -z/c)\) y\((t +z/c)\).

Fuentes de Ondas Planas

Estas soluciones se denominan ondas planas porque en cualquier\(z\) plano constante los campos son constantes y no varían con las\(y\) coordenadas\(x\) y.

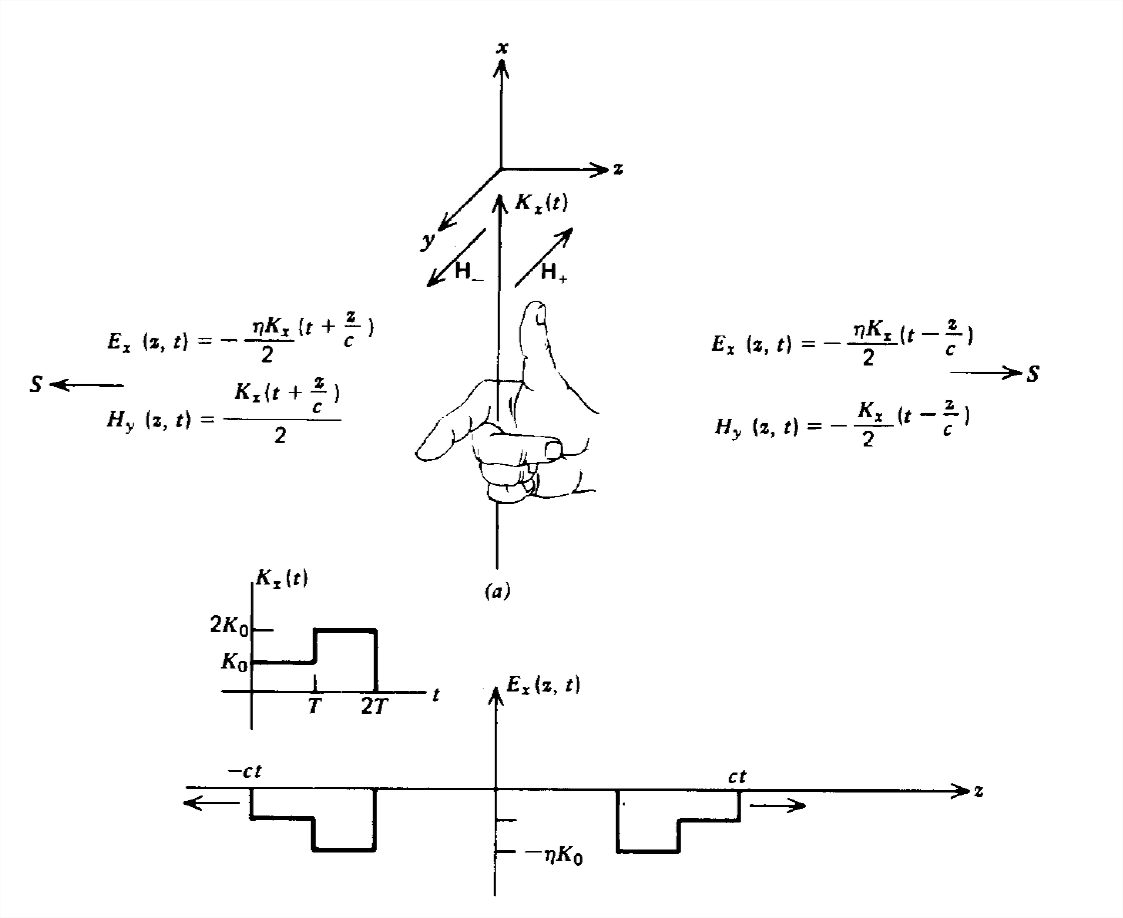
La fuente idealizada de una onda plana es una hoja de corriente variable en el tiempo de extensión infinita que tomamos para ser\(x\) dirigida,

La figura 7-4 (a)\(E_{-}\left ( t \right )\) at\(z =0\) es un pulso de escalera. (b)\(E_{-}\left ( \phi \right )\) siempre tiene la misma forma de (a) cuando se traza versus\(\phi\). Aquí\(\phi=t+z/c\). (c) Cuando se grafica versus\(t\), el pulso se traduce en tiempo donde\(z\) debe ser negativo para mantenerse\(t\) positivo. d) Cuando se traza versus\(z\), se traduce pero no se invierte.

como se muestra en la Figura 7-5. A partir de la condición límite sobre la discontinuidad de tangencial\(\textbf{H}\), encontramos que la hoja de corriente\(x\) -dirigida da lugar a un campo magnético\(y\) -dirigido:

\[ H_{y}\left ( z=0_{+} \right )-H_{y}\left ( z=0_{-} \right )=-K_{x}\left ( t \right ) \nonumber \]

En general, una hoja de corriente uniforme da lugar a un campo magnético perpendicular a la dirección del flujo de corriente pero en el plano de la lámina. Por lo tanto, para generar un campo magnético\(x\)\(y\) dirigido, se requiere una corriente superficial dirigida.

Como no hay otras fuentes, las olas deben alejarse de la lámina para que las soluciones en cada lado de la lámina sean de la forma

\ [H_ {y}\ left (z, t\ right) =\ left\ {\ begin {matrix}
H_ {+}\ left (t-z/c\ right)\\
H_ {-}\ left (t+z/c\ right)
\ end {matrix}\ right. \ quad E_ {x}\ izquierda (z, t\ derecha) =\ izquierda\ {\ comenzar {matriz}
\ eta H_ {+}\ izquierda (t-z/c\ derecha),\ quad z>0\\
-\ eta H_ {-}\ izquierda (t+z/c\ derecha),\ quad z<0
\ end {matriz}\ derecha. \ nonumber\]

Porque\(z >0\), las ondas se propagan sólo en la\(z\) dirección positiva. A falta de otras fuentes o límites, no puede haber olas que viajen negativamente en esta región. De manera similar para\ z <0 (\), solo tenemos ondas que se propagan en la\(-z\) dirección. Además de la condición límite de (22), el componente tangencial de\(\textbf{E}\) debe ser continuo a través de la lámina en\( z =0\)

\ [\ izquierda. \ begin {matrix} H_ {+}\ izquierda (t\ derecha) -H_ {-}\ izquierda (t\ derecha) =-K_ {x}\ izquierda (t\ derecha)
\\ eta\ izquierda [H_ {+}\ izquierda (t\ derecha) +H_ {-}\ izquierda (t\ derecha)\ derecha] =0
\ end {matriz}\ derecha\ derecha\ derecha H_ {+}\ izquierda (t\ derecha) =-H_ {-}\ izquierda (t\ derecha) =\ frac {-K_ {x}\ izquierda (t\ derecha)} {2}\ nonumber\]

Figura 7-5 (a) Una onda plana polarizada linealmente es generada por una hoja de corriente infinita. El campo eléctrico se encuentra en la dirección opuesta a la corriente a cada lado de la lámina. El campo magnético es perpendicular a la corriente pero en el plano de la hoja actual y en direcciones opuestas como lo da la regla de la derecha a cada lado de la hoja. El flujo de potencia\(\textbf{S}\) es así perpendicular a la corriente y a la hoja. b) Las soluciones de campo para\(t >2 T\) si la fuente de corriente es un pulso escalonado en el tiempo.

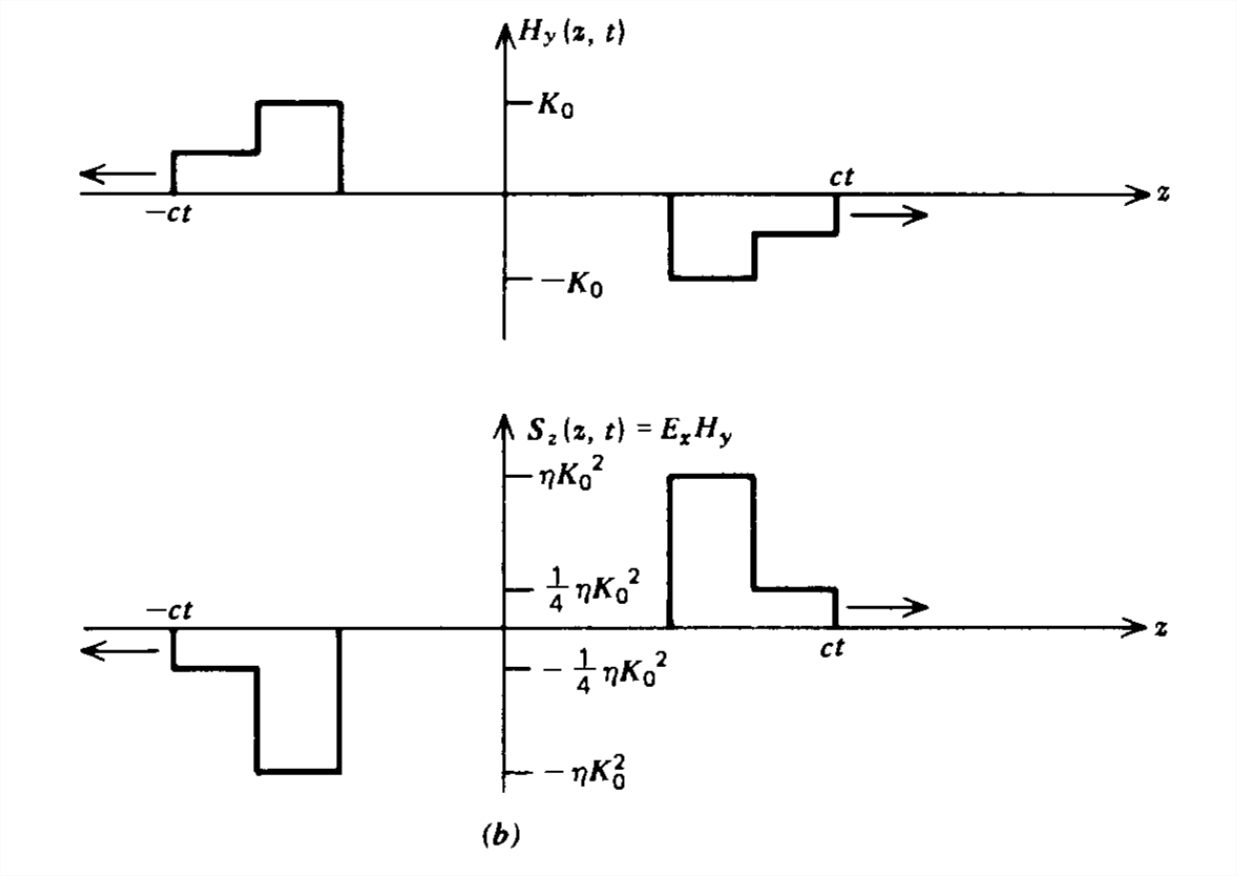
para que los campos eléctricos y magnéticos tengan la misma forma que la corriente. Debido a que la forma de tiempo y espacio de los campos permanece sin cambios a medida que las ondas se propagan, se dice que los medios dieléctricos lineales no son dispersivos.

Obsérvese que el campo eléctrico en\(z =0\) está en la dirección opuesta a la corriente, por lo que la potencia por unidad de área entregada por la hoja de corriente,

\[ -\textbf{E}\left ( z=0,t \right )\cdot \textbf{K}_{x}\left ( t \right )=\frac{\eta K_{x}^{2}\left ( t \right )}{2} \nonumber \]

es igualmente arrastrado por el vector Poynting en cada lado de la hoja:

\ [\ textbf {S}\ izquierda (z=0\ derecha) =\ textbf {E}\ veces\ textbf {H} =\ izquierda\ {\ comenzar {matriz}
\ frac {\ eta K_ {x} ^ {2}\ izquierda (t\ derecha)} {4}\ textbf {i} _ {x}, quad\ z> 0\
\\ frac -\ eta K_ {x} ^ {2}\ izquierda (t\ derecha)} {4},\ quad z<0
\ end {matriz}\ derecha. \ nonumber\]

Una breve introducción a la teoría de la relatividad

Las ecuaciones de Maxwell muestran que las ondas electromagnéticas se propagan a la velocidad\(c_{0}=1/\sqrt{\varepsilon_{0}\mu _{0}}\) en vacío. Nuestra intuición natural nos diría que si nos movíamos a una velocidad\(v\) mediríamos una velocidad de ola de\(c_{0}-v\) cuando nos movemos en la misma dirección que la ola, y una velocidad\(c_{0}+v\) cuando nos movemos en sentido contrario. Sin embargo, nuestra intuición estaría equivocada, porque en ninguna parte del espacio libre, aparecen las ecuaciones de Maxwell sin fuente la velocidad del observador. Las ecuaciones de Maxwell predicen que la velocidad de las ondas electromagnéticas es co para todos los observadores sin importar su velocidad relativa. Esta suposición es un postulado fundamental de la teoría de la relatividad y ha sido verificada por todos los experimentos. El experimento más notable fue realizado por A. A. Michelson y E. W. Morley a finales del siglo XIX, donde demostraron que la velocidad de la luz reflejada entre los espejos es la misma ya sea que se propague en dirección paralela o perpendicular a la velocidad de la tierra. Este postulado requirió una revisión de las nociones habituales de tiempo y distancia.

Si la hoja de corriente superficial de la Sección 7-3-3 se enciende primero en\(t = 0\), la posición del frente de onda a cada lado de la hoja en un momento\(t\) posterior obedece a la igualdad

\[ z^{2}-c_{0}^{2}t^{2}=0 \nonumber \]

De manera similar, un observador en un sistema de coordenadas que se mueve a velocidad constante\(u\textbf{i}_{z}\), que se alinea con la hoja actual en\(t=0\) encuentra la posición del frente de onda para obedecer la igualdad

\[ z'^{2}-c_{0}^{2}t'^{2}=0 \nonumber \]

Los dos sistemas de coordenadas deben estar relacionados por una transformación lineal de la forma

\[ z'=a_{1}z+a_{2}t,\quad t'=b_{1}z+b_{2}t \nonumber \]

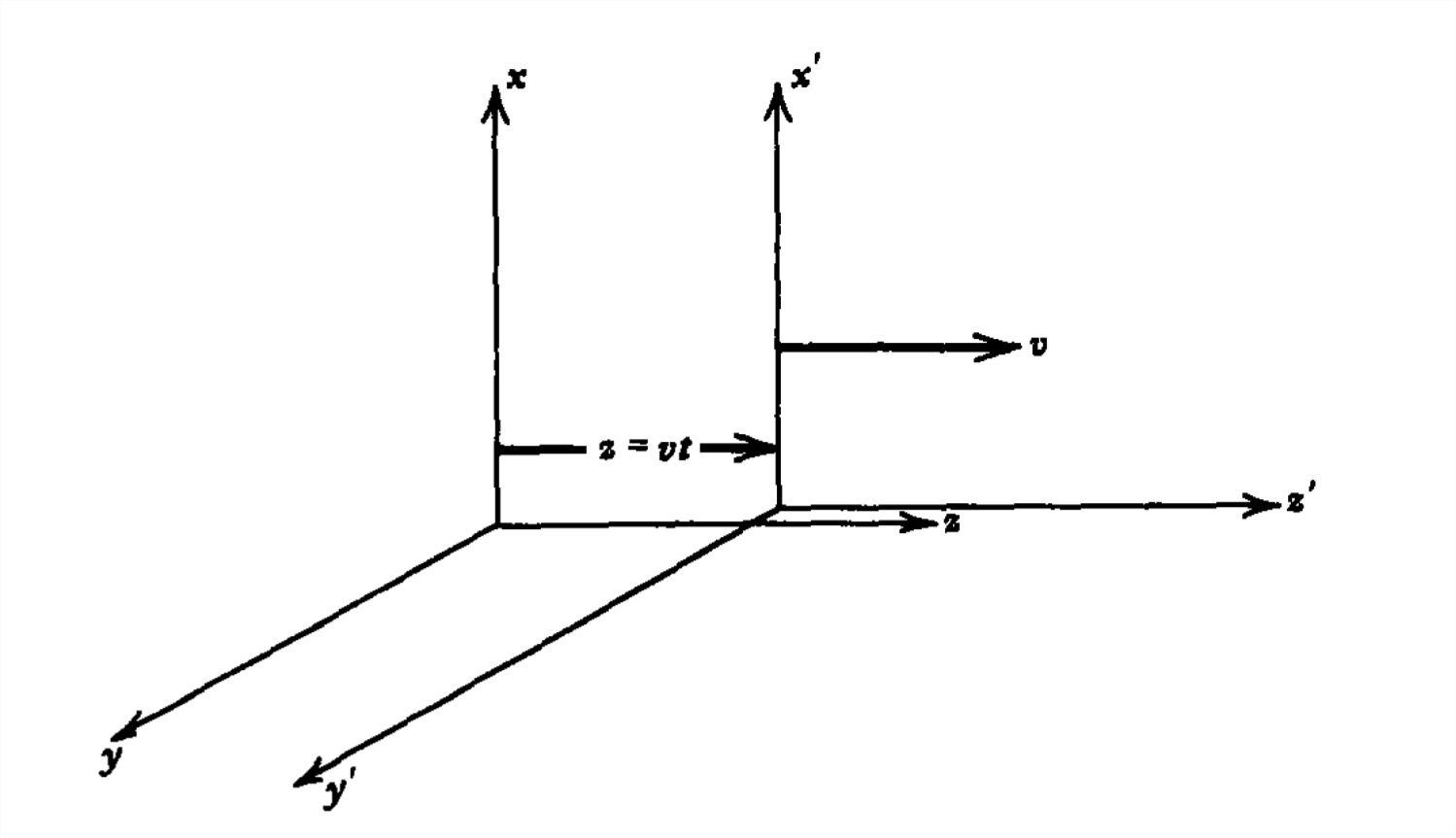
La posición del origen del bastidor móvil\((z'=0)\) medida en el bastidor estacionario es\(z = vt\), como se muestra en la Figura 7-6, de manera que\(a_{1}\) y\(a_{2}\) se relacionan como

\[ 0=a_{1}vt+a_{2}t\Rightarrow a_{1}v+a_{2}=0 \nonumber \]

También podemos equiparar las dos igualdades de (27) y (28),

\[ z^{2}-c_{0}^{2}t^{2}=z'^{2}-c_{0}^{2}t'^{2}=\left ( a_{1}z+a_{2}t \right )^{2}-c_{0}^{2}\left ( b_{1}z+b_{2}t \right ) \nonumber \]

para que la combinación de términos rinda

\[ z^{2}\left ( 1-a_{1}^{2}+c_{0}^{2}b_{1}^{2} \right )-c_{0}^{2}t^{2}\left ( 1+\frac{a_{2}^{2}}{c_{0}^{2}}-b_{2}^{2} \right )-2\left ( a_{1}a_{2}-c_{0}^{2}b_{1}b_{2} \right )zt=0 \nonumber \]

Ya que (32) debe ser cierto para todos\(z\) y\(t\), cada uno de los coeficientes debe ser cero, lo que con (30) da soluciones

\ [a_ {1} =\ frac {1} {\ sqrt {1-\ izquierda (v/c_ {0}\ derecha) ^ {2}}},\ quad b_ {1} =\ frac {-v/c_ {0} ^ {2}} {\ sqrt {1-\ izquierda (v/c_ {0}\ derecha) ^ {2}}\\
a_ 2} =\ frac {-v} {\ sqrt {1-\ izquierda (v/c_ {0}\ derecha) ^ {2}},\ quad b_ {2} =\ frac {1} {\ sqrt {1-\ izquierda (v/c_ {0}\ derecha) ^ {2}}}\ nonumber\]

Figura 7-6 El sistema de coordenadas cebado se mueve a velocidad constante\(v\textbf{i}_{z}\), con respecto a un sistema de coordenadas estacionario. La velocidad espacial libre de una onda electromagnética es\(c_0\) medida por observadores en cualquiera de los sistemas de coordenadas sin importar la velocidad\(v\).

Las transformaciones de (29) son entonces

\[ z'=\frac{z-vt}{\sqrt{1-\left ( v/c_{0} \right )^{2}}},\quad t'=\frac{t-vz/c_{0}^{2}}{\sqrt{1-\left ( v/c_{0} \right )^{2}}} \nonumber \]

y son conocidas como las transformaciones de Lorentz. Las longitudes y los intervalos de tiempo medidos son diferentes para los observadores que se mueven a diferentes velocidades. Si la velocidad\(v\) es mucho menor que la velocidad de la luz, (34) se reduce a las transformaciones galileanas,

\[ \lim_{v/c\ll 1}z'\approx z-vt,\quad t'\approx t \nonumber \]

que describen nuestras experiencias habituales a velocidades no relativistas. Las coordenadas perpendiculares al movimiento no se ven afectadas por la velocidad relativa entre los fotogramas de referencia

\[ x'=x,\quad y'=y \nonumber \]

El desarrollo continuo de la teoría de la relatividad está más allá del alcance de este texto y merece un curso en sí mismo. Aplicando la transformación de Lorentz a la ley de Newton y a las ecuaciones de Maxwell arroja nuevos resultados que a primera aparición parecen contrarios a nuestras experiencias porque vivimos en un mundo donde la mayoría de las velocidades materiales son mucho menores que\(c_0\). Sin embargo, los experimentos continuos en escalas de tiempo y espacio tan dispares como entre la física atómica y la astronomía verifican las predicciones de la teoría de la relatividad, en parte engendradas por las ecuaciones de Maxwell.