7.5: Incidencia Normal en un Conductor Perfecto

Una onda plana uniforme con campo eléctrico\(x\) dirigido es normalmente incidente sobre un plano perfectamente conductor en\(z =0\), como se muestra en la Figura 7-13. La presencia del límite da lugar a una onda reflejada que se propaga en la\(-z\) dirección. No hay campos dentro del conductor perfecto. Los campos de incidentes conocidos que viajan en la\(+z\) dirección pueden escribirse como

\ [\ textbf {E} _ _ {i}\ izquierda (z, t\ derecha) =\ textrm {Re}\ izquierda (\ hat {E} _ _ {i} e^ {j\ izquierda (\ omega t-kz\ derecha)}\ textbf {i} _ {x}\ derecha)
\\ textbf {H} _ {i}\ izquierda (z, t\ derecha) =\ textrm {Re}\ izquierda (\ frac {\ sombrero {E} _ {i}} {\ eta_ {0}} e^ {j\ izquierda (\ omega t-kz\ derecha)}\ textbf {i} _ {y}\ derecha)\ nonumber\]

mientras que los campos reflejados que se propagan en la\(-z\) dirección son similares

\ [\ textbf {E} _ {r}\ izquierda (z, t\ derecha) =\ textrm {Re}\ izquierda (\ hat {E} _ {r} e^ {j\ izquierda (\ omega t+kz\ derecha)}\ textbf {i} _ {x}\ derecha)\
\ textbf {H} _ {r}\ izquierda (z, t\ derecha) =\ textrm {Re}\ izquierda (\ frac {-\ hat {E} _ {r}} {\ eta_ {0}} e^ {j\ izquierda (\ omega t+kz\ derecha)}\ textbf {i} _ {y}\ derecha)\ nonumber\]

donde en el espacio libre sin pérdidas

\[ \eta_{0}=\sqrt{\mu _{0}/\varepsilon _{0}},\quad k=\omega \sqrt{\varepsilon _{0}\mu _{0}} \nonumber \]

Observe la diferencia de signo menos en los factores de fase exponenciales espaciales de (1) y (2) a medida que las olas viajan en direcciones opuestas. La amplitud de los campos magnéticos incidentes y reflejados viene dada por la relación entre la amplitud del campo eléctrico y la impedancia de onda, como se deriva en la Ec. (15) de la Sección 7-3-2. El signo negativo frente al campo magnético reflejado para la onda en la\(-z\) dirección surge porque el flujo de potencia\(\textbf{S}_{r}=\textbf{E}_{r}\times \textbf{H}_{r} \) en la onda reflejada también debe estar en la\(-z\) dirección.

Figura 7-13 Una onda plana uniforme que normalmente incide sobre un conductor perfecto tiene un campo eléctrico cero en la superficie conductora, requiriendo así una onda reflejada. La fuente de esta onda reflejada es la corriente superficial en\(z=0\), que es igual al campo magnético allí. Los campos eléctricos y magnéticos totales están\(90^{\circ }\) desfasados en el tiempo y el espacio.

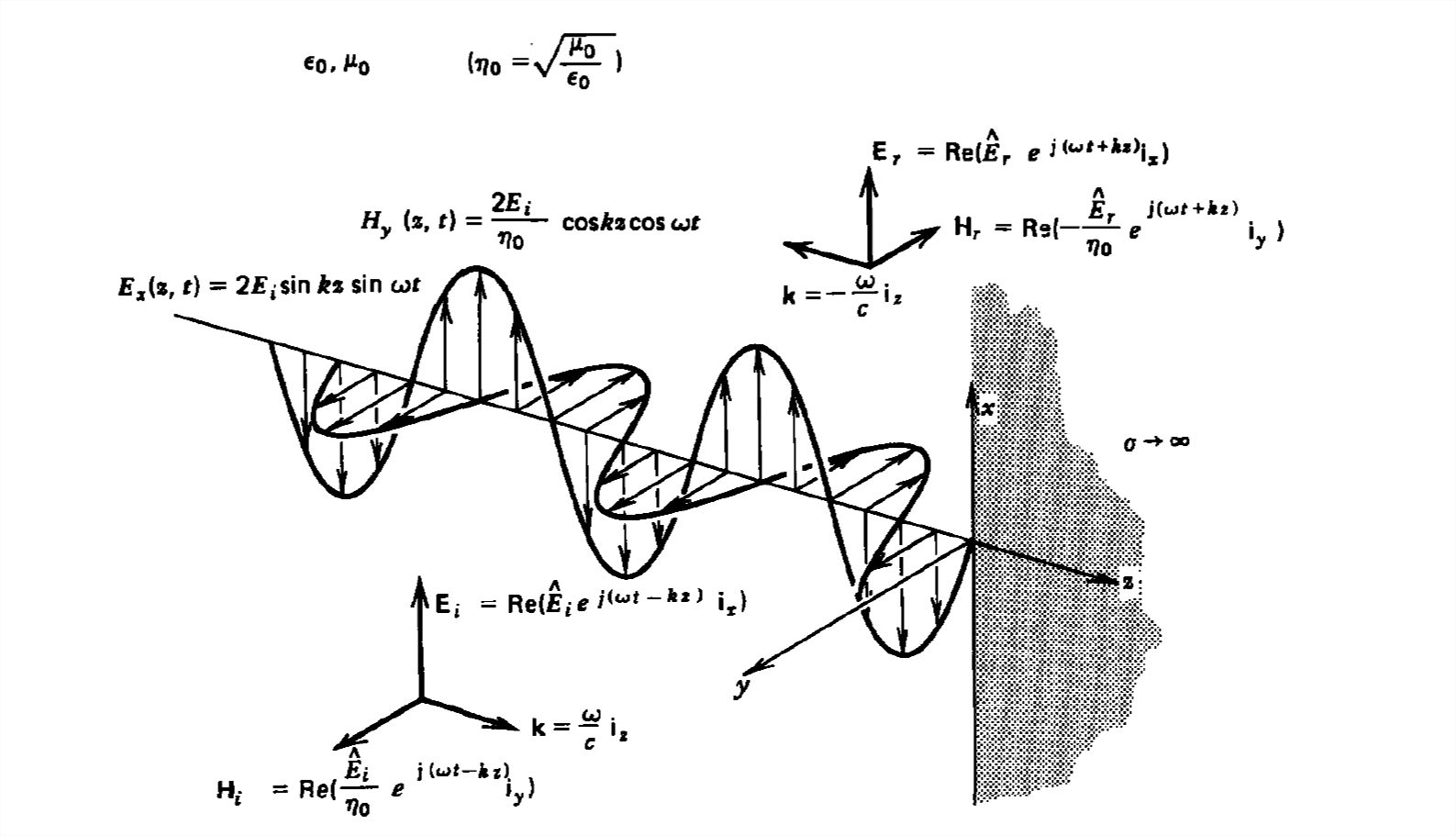
Los campos eléctricos y magnéticos totales son solo la suma de los campos incidentes y reflejados. El único parámetro desconocido se\(E_{r}\) puede evaluar a partir de la condición de límite en\(z =0\) donde el componente tangencial de\(\textbf{E}\) debe ser continuo y, por lo tanto, cero a lo largo del conductor perfecto:

\[ \hat{E}_{i}+\hat{E}_{r}=0\Rightarrow \hat{E}_{r}=-\hat{E}_{i} \nonumber \]

Los campos totales son entonces la suma del incidente y campos reflejados

\ [\ begin {align}
\ textbf {E} _ {x}\ izquierda (z, t\ derecha) & =\ textbf {E} _ {i}\ izquierda (z, t\ derecha) +\ textbf {E} _ {r}\ izquierda (z, t\ derecha)\ nonumber\\ & =\ textrm {Re}\ izquierda [\ hat {E} {i}\ izquierda (e^ {-jkz} -e^ {+jkz}\ derecha) e^ {j\ omega t}\ derecha]\ nonumber\\ &
=2E_ {i}\ sin kz\ sin\ omega t\ nonumber\\\ textbf {H} _ {y}\ izquierda (z, t\ derecha) & =\ textbf {H} _ {i}\ izquierda (z, t\ derecha) +\ textbf {H} _ {r}\ izquierda (z, t\ derecha)\ nonumber\\ &=\ textrm {Re}\ izquierda (\ frac {\ hat E {} _ {i}} {\ eta _ {0}}\ izquierda (e^ {-jkz} +e^ {+jkz}\ derecha) e^ {j\ omega t}\ derecha)\ nonumber\\ &=\ frac {2E_ {i}} {\ eta _ {0}}\ cos kz\ cos\ cos\ omega t
\ end {align}\ nonumber\]

donde llevamos\(\hat{E}_{i}=E_{i}\) para ser reales. Los campos eléctrico y magnético están\(90^{\circ }\) desfasados entre sí tanto en el tiempo como en el espacio. Observamos que las dos soluciones de ondas viajeras opuestas se combinaron para una solución de onda estacionaria. La solución total no se propaga sino que es una solución sinusoidal permanente en el espacio cuya amplitud varía sinusoidalmente en el tiempo.

Una corriente superficial fluye en el conductor perfecto\(z =0\) debido a la discontinuidad en componente tangencial de\(\textbf{H}\),

\[ K_{x}=H_{y}\left ( z=0 \right )=\frac{2E_{i}}{\eta_{0}}\cos \omega t \nonumber \]

dando lugar a una fuerza por unidad de área sobre el conductor,

\[\textbf{F}=\frac{1}{2}\textbf{K}\times \mu _{0}\textbf{H}=\frac{1}{2}\mu _{0}H_{y}^{2}\left ( z=0 \right )\textbf{i}_{z}=2\varepsilon _{0}E_{i}^{2}\cos ^{2}\omega t\textbf{i}_{z} \nonumber \]

conocida como la presión de radiación. El factor de\(\frac{1}{2}\) surge en (7) porque la fuerza sobre una corriente superficial es proporcional al valor promedio del campo magnético en cada lado de la interfaz, siendo aquí cero para\(z = 0_+\).