7.10: Aplicaciones a la Óptica

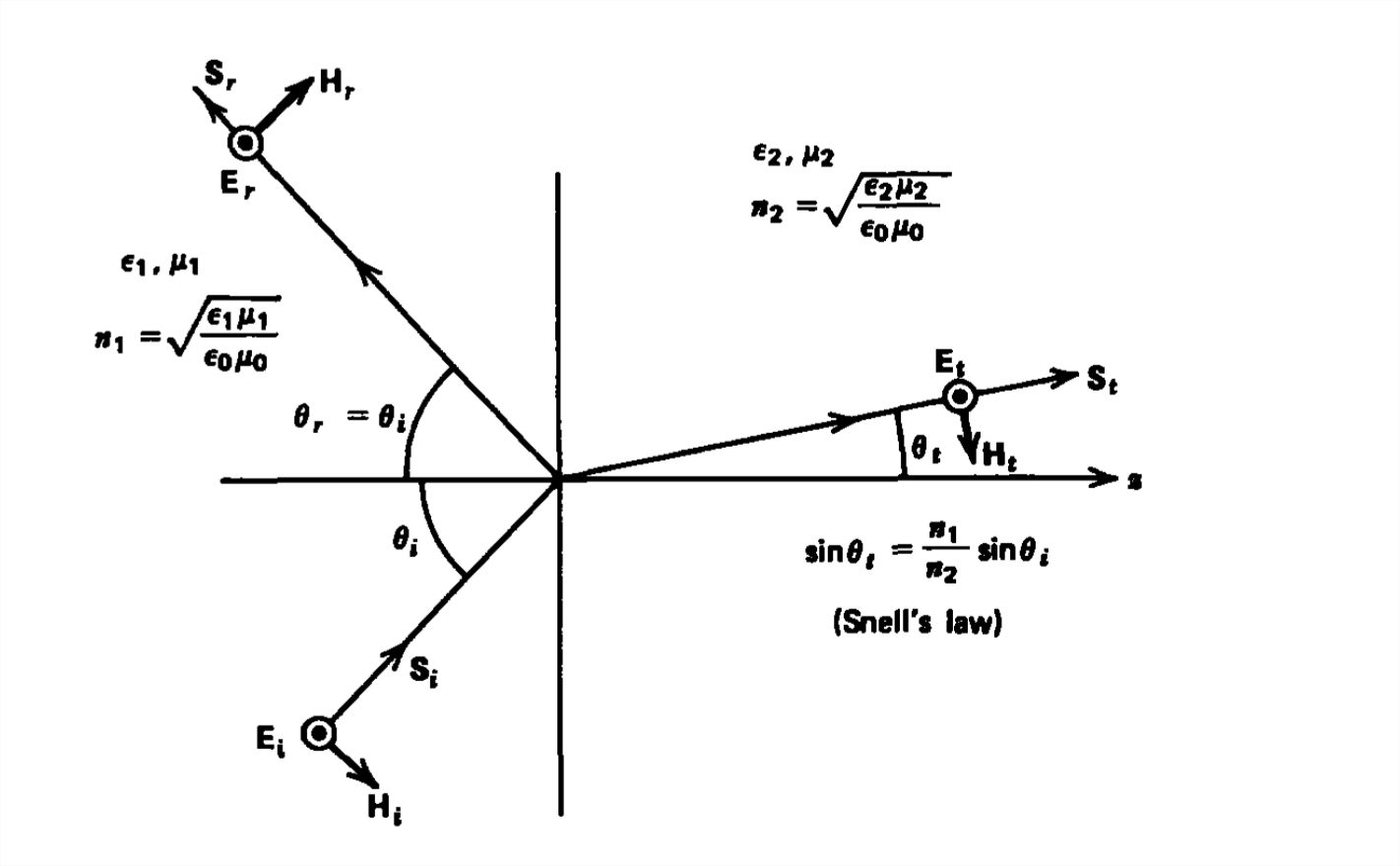
La reflexión y refracción de las ondas electromagnéticas que inciden oblicuamente sobre la interfaz entre medios lineales disímiles sin pérdida se rigen por las dos reglas ilustradas en la Figura 7-19:

1. El ángulo de incidencia es igual al ángulo de reflexión.
2. Las ondas que inciden desde una media de alta velocidad de la luz (bajo índice de refracción) a una de baja velocidad (alto índice de refracción) se doblan hacia la normal. Si la onda es incidente desde un medio de baja velocidad (índice alto) a alta velocidad (índice bajo), la luz se dobla alejándose de la normal. El incidente y los ángulos refractados están relacionados por la ley de Snell.

Figura 7-19 Un resumen de los fenómenos de reflexión y refracción a través de la interfaz que separa dos medios lineales. Cuando\(\theta _{i}=\theta _{B}\) (ángulo de Brewster), no hay rayo reflejado. Cuando\(\theta _{i}>\theta _{c}\) (ángulo crítico), los campos transmitidos decaen con\(z\).

La mayoría de los materiales ópticos, como el vidrio, tienen una permeabilidad del espacio libre\(\mu _{0}\). Por lo tanto, el ángulo de no reflexión de Brewster solo existe si el\(\textbf{H}\) campo es paralelo al límite.

En el ángulo crítico, que solo puede existir si la luz viaja de un material de alto índice de refracción (baja velocidad de la luz) a uno de bajo índice (alta velocidad de la luz), existe un campo transmitido que decae con la distancia como una onda plana no uniforme. Sin embargo, no existe una potencia promedio en el tiempo transportada por esta onda evanescente de manera que se refleja toda la potencia promedio en el tiempo. En esta sección se describen brevemente diversas aplicaciones de estos ángulos especiales y las reglas que rigen la reflexión y la refracción.

Reflejos de un espejo

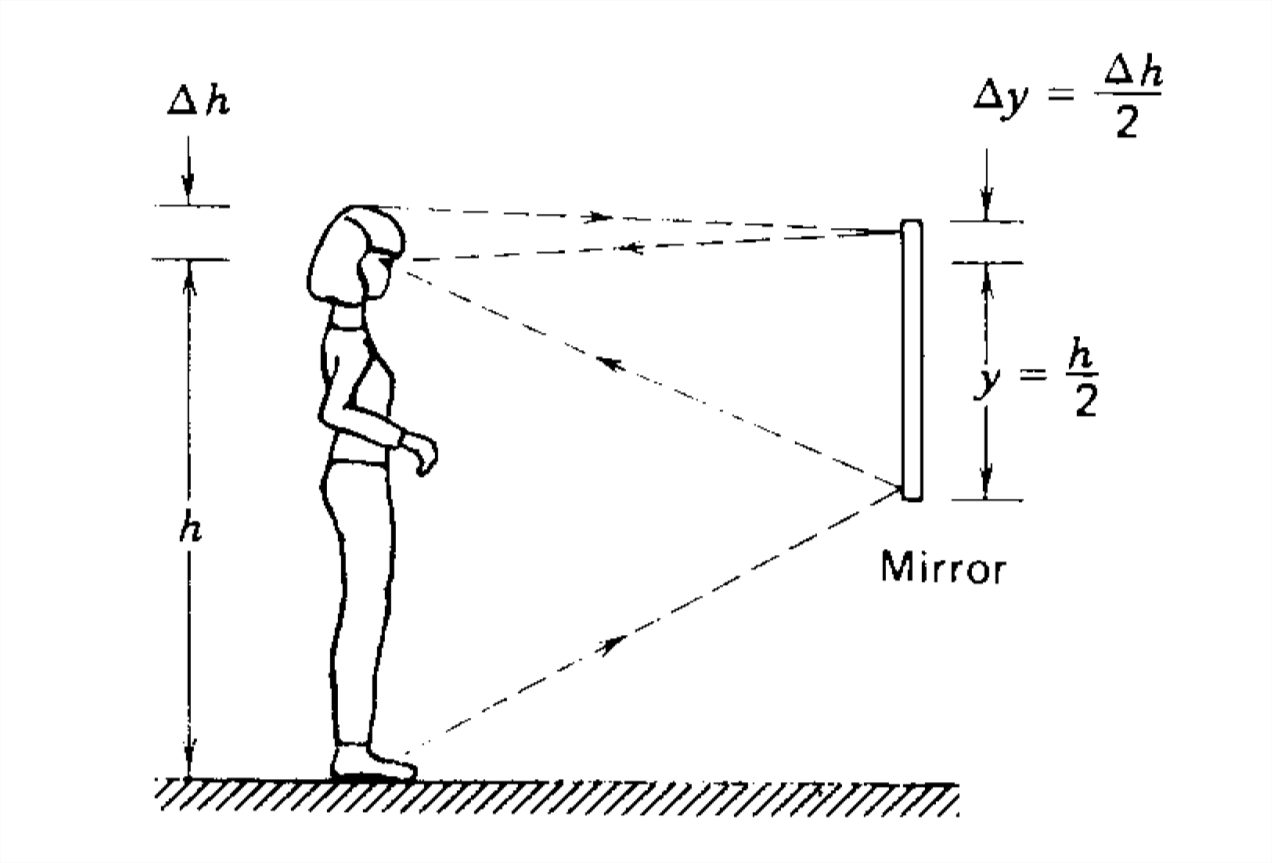
Una persona tiene sus ojos a la altura\(h\) por encima de sus pies y una altura\(\Delta h\) por debajo de la parte superior de su cabeza, como en la Figura 7-20. Un espejo en frente se extiende una distancia\(\Delta y\) por encima de los ojos y una distancia\(y\) por debajo. ¿Qué tan grande debe\(y\) y\(\Delta y\) ser para que la persona vea toda su imagen? La luz reflejada de la persona al espejo debe reflejarse nuevamente en los ojos de la persona. Dado que el ángulo de incidencia es igual al ángulo de reflexión, la Figura 7-20 muestra que\(\Delta y=\Delta h/2\) y\(y =h/2\).

Desplazamiento lateral de un rayo de luz

Un rayo de luz incide desde el espacio libre sobre un medio transparente con índice de refracción\(n\) en ángulo\(\theta _{i}\), como se muestra en la Figura 7-21. El ángulo de la luz transmitida viene dado por la ley de Snell:

\[ \sin \theta _{t}=\left ( 1/n \right )\sin \theta _{i} \nonumber \]

Figura 7-20 Debido a que el ángulo de incidencia es igual al ángulo de reflexión, una persona puede ver toda su imagen si el espejo se extiende la mitad de la distancia de extensión por encima y por debajo de los ojos.

Figura 7-21 Un rayo de luz incidente sobre una placa de vidrio sale de la placa hacia el medio original paralelo a su trayectoria original pero desplazado lateralmente.

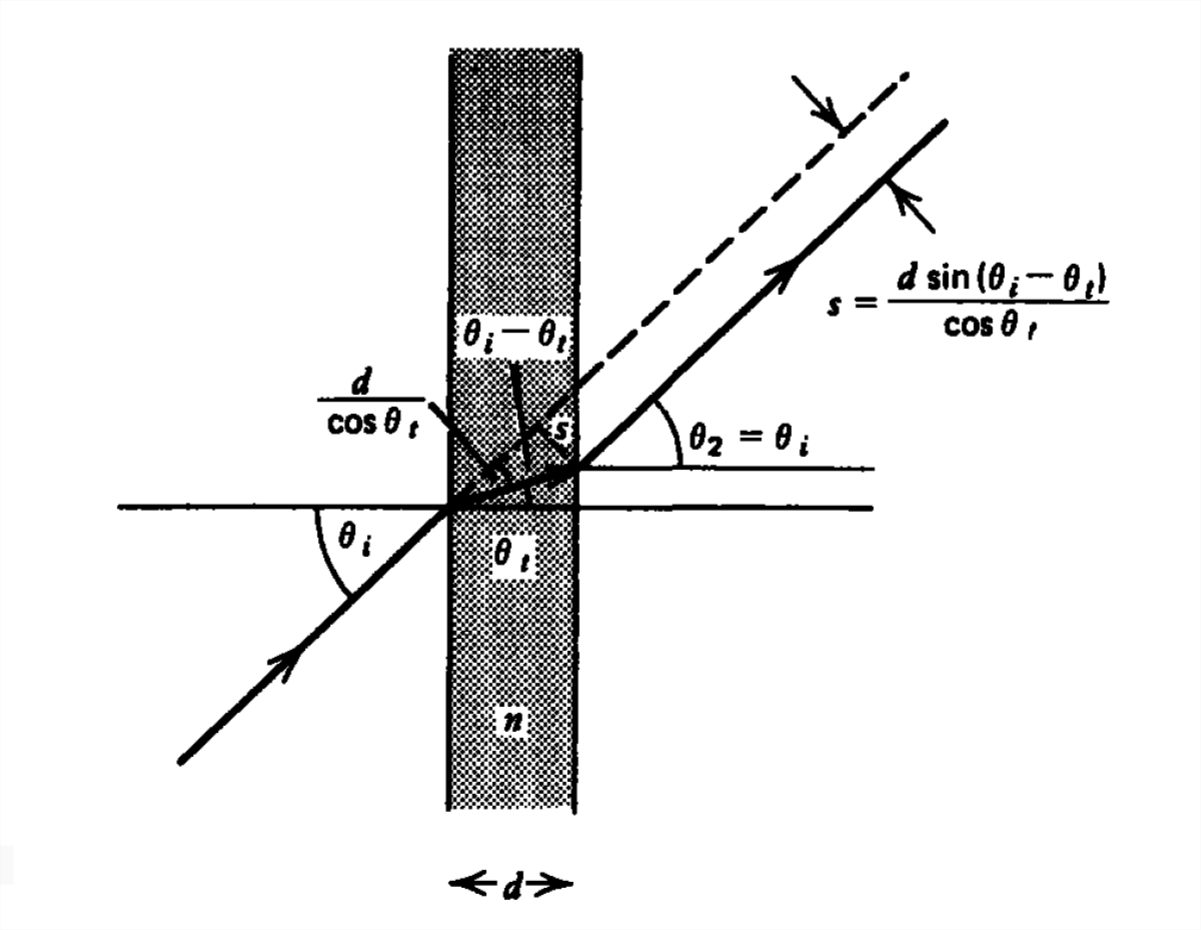
Cuando esta luz incide en la segunda interfaz, el ángulo\(\theta _{t}\) es ahora el ángulo incidente para que el ángulo\(\theta _{2}\) transmitido vuelva a ser dado por la ley de Snell:

\[ \sin \theta _{2}=n\sin \theta _{t}=\sin \theta _{i} \nonumber \]

para que la luz salga en el ángulo de incidencia original\(\theta _{i}\). Sin embargo, ahora se desplaza por la cantidad:

\[ s=\frac{d\sin \left ( \theta _{i}-\theta _{t} \right )}{\cos \theta _{t}} \nonumber \]

Si la placa es de vidrio con índice de refracción\(n = 1.5\) y espesor\(d = 1 \textrm{mm}\) con ángulo incidente\( \theta _{i}=30^{\circ }\), el ángulo\( \theta _{t}\) en el vidrio es

\[  \sin \theta _{t}=0.33\Rightarrow \theta _{t}=19.5^{\circ } \nonumber \]

para que el desplazamiento lateral sea\(s = 0.19 \textrm{mm}\).

Polirización por reflexión

La luz no polarizada incide sobre la pieza de vidrio en la Sección 7-10-2 con índice de refracción\(n = 1.5\). La luz no polarizada tiene ambas\(\textbf{E}\) y\(\textbf{H}\) paralela a la interfaz. Suponemos que la permeabilidad del vidrio es igual a la del espacio libre y que la luz incide en el ángulo de Brewster\(\theta _{B}\) para la luz polarizada con\(\textbf{H}\) paralelo a la interfaz. Los ángulos incidentes y transmitidos son entonces

\ [\ tan\ theta _ {B} =\ sqrt {\ varepsilon/\ varepsilon _ {0}} =n\ Rightarrow\ theta _ {B} =56.3^ {\ circ}\
\\ tan\ theta _ {t} =\ sqrt {\ varepsilon _ {0}/\ varepsilon} =1/n Fila derecha\ theta _ {t} =33.7^ {\ circ}\ nonumber\]

El ángulo de Brewster también se llama ángulo de polarización porque se puede utilizar para separar las dos polarizaciones ortogonales. La polarización, cuyo\(\textbf{H}\) campo es paralelo a la interfaz, se transmite completamente en la primera interfaz sin reflexión. La otra polarización con campo eléctrico paralelo a la interfaz se transmite y refleja parcialmente. En la segunda interfaz (espacio libre de vidrio), la luz incide en ángulo\(\theta _{t}\). De (5) vemos que este ángulo es el ángulo de Brewster con\(\textbf{H}\) paralelo a la interfaz para la luz incidente desde el lado del vidrio hacia la interfaz de espacio libre de vidrio. Por otra parte, el paralelo H a la polarización de la interfaz se transmite por completo mientras que el\(\textbf{E}\) paralelo a la polarización de la interfaz se refleja parcialmente y se transmite parcialmente. Así, la onda reflejada está totalmente polarizada con un campo eléctrico paralelo a la interfaz. Las ondas transmitidas, aunque compuestas por ambas polarizaciones, tienen la mayor amplitud con\(\textbf{H}\)

Figura 7-22 La luz no polarizada incidente sobre el vidrio con\(\mu = \mu _{0}\) puede ser polarizada por reflexión si es incidente en el ángulo de Brewster para la polarización con\(\textbf{H}\) paralelo a la interfaz. La luz transmitida se polariza más con\(\textbf{H}\) paralelo a la interfaz al agregar más placas de vidrio paralelas.

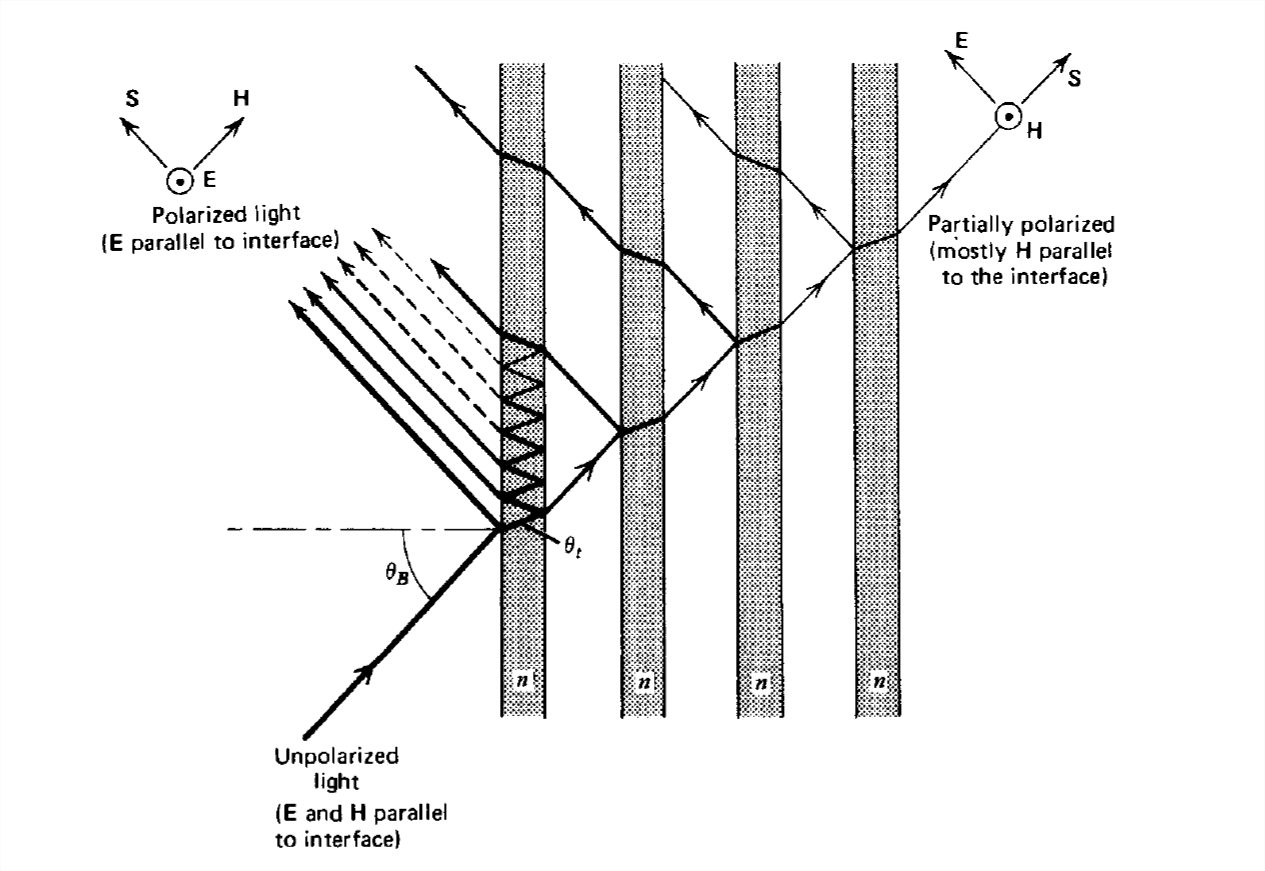
paralelo a la interfaz porque se transmitió completamente sin reflexión en ambas interfaces.

Al pasar la luz transmitida a través de otra pieza paralela de vidrio, la polarización con campo eléctrico paralelo a la interfaz disminuye aún más debido a que se refleja parcialmente, mientras que la otra polarización se transmite completamente. Con más elementos de vidrio, como en la Figura 7-22, la luz transmitida puede hacerse esencialmente polarizada completamente con\(\textbf{H}\) campo paralelo a la interfaz.

Propagación de Luz en Agua

a) Fuente sumergida

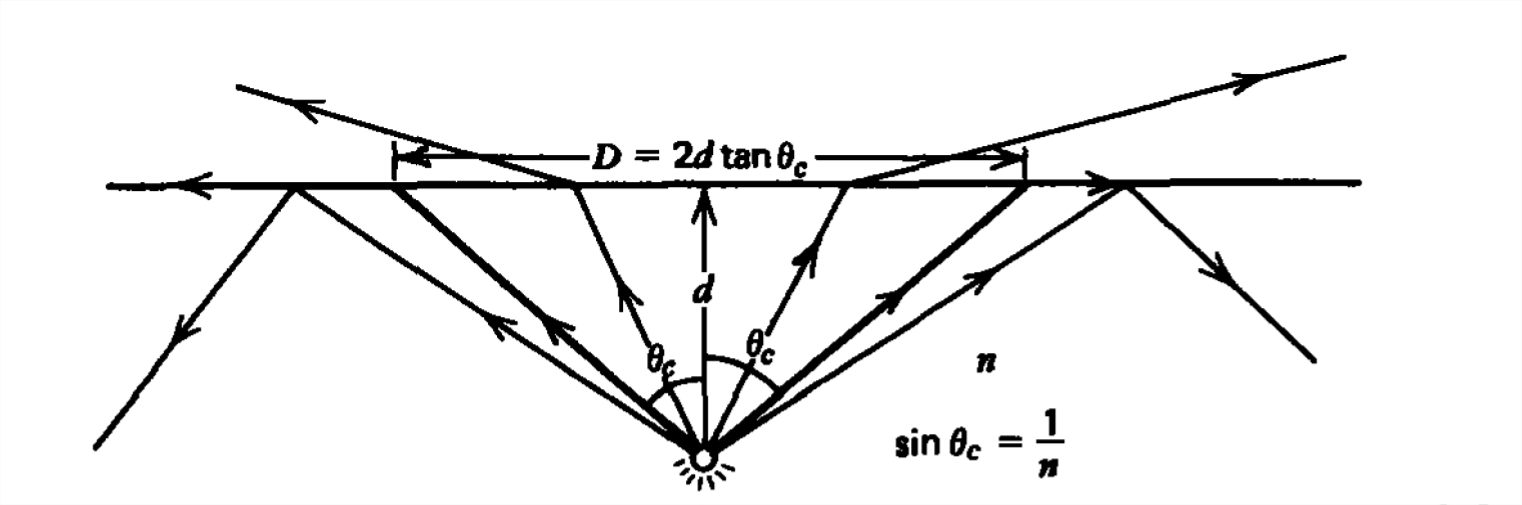
Una fuente de luz es una distancia d por debajo de la superficie del agua con índice de refracción\(n = 1.33\), como en la Figura 7-23. Los rayos emanan de la fuente como un cono. Esos rayos en un ángulo desde la normal mayor que el ángulo crítico,

\[ \sin \theta _{c}=1/n\Rightarrow \theta _{c}=48.8^{\circ } \nonumber \]

no se transmiten al aire sino que se someten a una reflexión interna total. Un círculo de luz con diámetro

\[ D=2d\tan \theta _{c}\approx 2.28d \nonumber \]

luego se forma en la superficie del agua debido a la luz que sale.

b) Peces debajo de un bote

Un pez nada debajo de una embarcación circular de diámetro\(D\), como en la Figura 7-24. Al intentar ver a los peces desde el aire de arriba, el rayo de luz incidente se inclina hacia la normal. La región debajo de la embarcación que vemos desde arriba está delimitada por los rayos de luz al pastoreo incidencia a la superficie\(\left ( \theta _{i}=\pi /2 \right )\) apenas entrando al agua\((n = 1.33)\) a los lados de la embarcación. El ángulo transmitido de estos rayos de luz se da de la ley de Snell como

\[ \sin \theta _{t}=\frac{\sin \theta _{i}}{n}=\frac{1}{n}\Rightarrow \theta _{t}=48.8^{\circ } \nonumber \]

Figura 7-23 Los rayos de luz que emanan de una fuente dentro de un medio de alto índice de refracción se reflejan totalmente internamente desde la superficie para ángulos mayores que el ángulo crítico. Se transmiten ángulos de incidencia menores.

Figura 7-24 Un pez no se puede ver desde arriba si nada por debajo de una embarcación circular dentro del cono delimitado por rayos de luz en incidencia de pastoreo entrando al agua al costado de la embarcación.

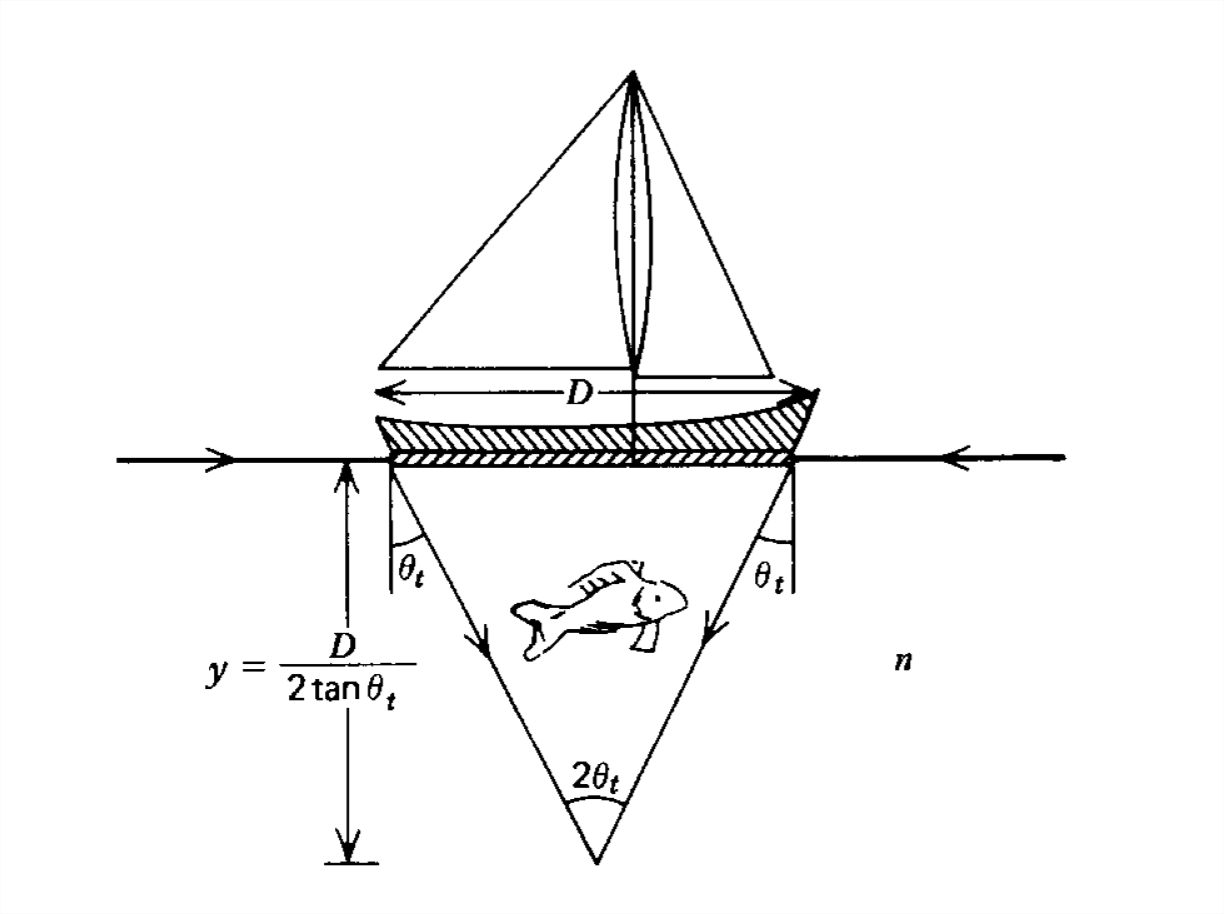
Estos rayos de todos los lados de la embarcación se cruzan en el punto a una distancia\(y\) por debajo de la embarcación, donde

\[ \tan \theta _{t}=\frac{D}{2y} \Rightarrow y=\frac{D}{2\tan \theta_{t}}\approx 0.44D \nonumber \]

Si el pez nada dentro del cono, con vértice en el punto\(y\) debajo del bote, no se puede ver desde arriba.

Prismas totalmente reflectantes

El triángulo rectángulo isóceles de vidrio en la Figura 7-25 tiene un índice de refracción de\(n = 1.5\) tal manera que el ángulo crítico para total

Figura 7-25 Un prisma totalmente reflectante. El índice de refracción\(n\) debe superar\(\sqrt{2}\) para que la luz incidente sobre la hipotenusa\(45^{\circ }\) supere el ángulo crítico.

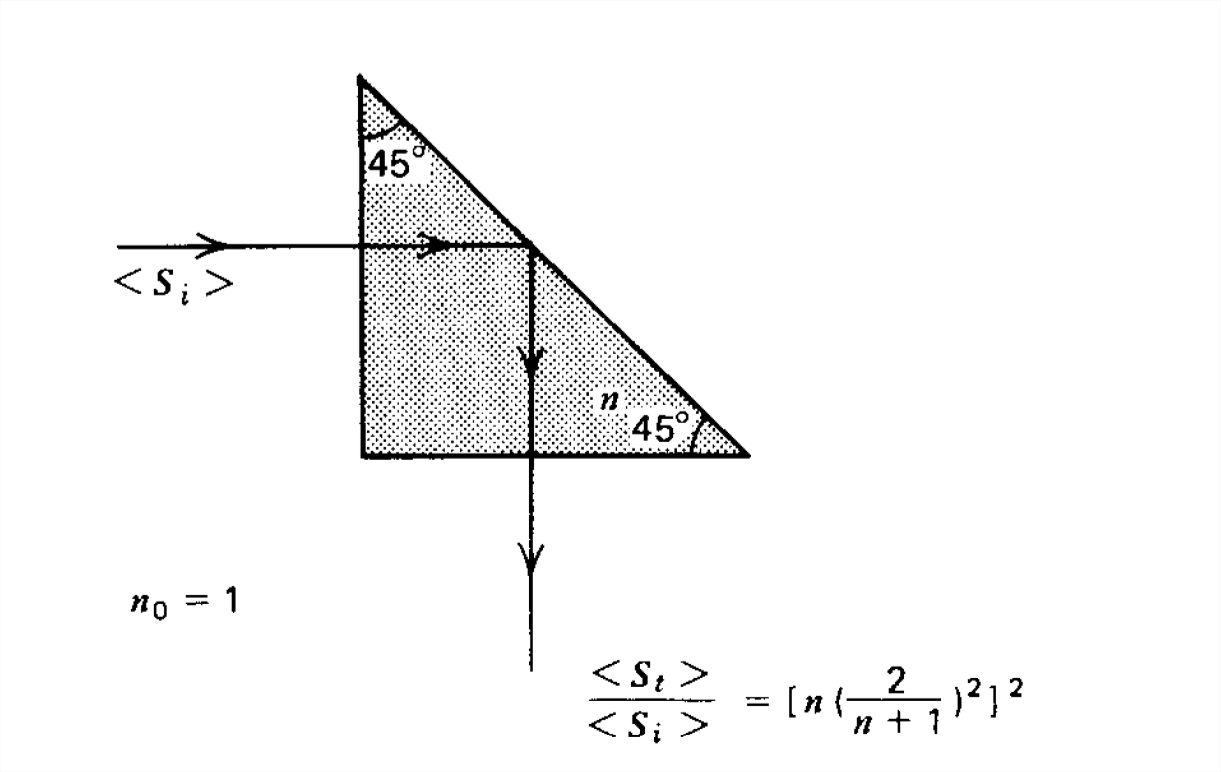
la reflexión interna es

\[ \sin \theta _{c}=\frac{1}{n}=\frac{1}{1.5}\Rightarrow \theta _{c}=41.8^{\circ } \nonumber \]

La luz es normalmente incidente sobre la cara vertical del prisma. El coeficiente de transmisión se da entonces en la Sección 7-6-1 como

\[ T_1=\frac{\hat{E}_{t}}{\hat{E}_{i}}=\frac{2\eta }{\eta +\eta _{0}}=\frac{2/n}{1+1/n}=\frac{2}{n+1}=0.8  \nonumber \]

donde porque la permeabilidad del prisma es igual a la del espacio libre\(n=\sqrt{\varepsilon /\varepsilon _{0}}\) mientras\(\eta /\eta _{0}=\sqrt{\varepsilon _{0} /\varepsilon}=1/n\). La luz transmitida es entonces incidente sobre la hipotenusa del prisma en un ángulo de\(45^{\circ }\), que excede el ángulo crítico para que no se transmita energía y la luz se refleje totalmente siendo girada en ángulo recto. La luz es entonces normalmente incidente sobre la cara horizontal con coeficiente de transmisión:

\[ T_2=\frac{\hat{E}_{2}}{0.8\hat{E}_{i}}=\frac{2\eta _{0} }{\eta +\eta _{0}}=\frac{2}{1/n+1}=\frac{2n}{n+1}=1.2  \nonumber \]

La amplitud del campo eléctrico resultante es entonces

\[ \hat{E}_{2}=T_{1}T_{2}\hat{E}_{i}=0.96\hat{E}_{i} \nonumber \]

La relación de densidad de potencia transmitida a incidente es

\[ \frac{<S>}{<S_{i}>}=\frac{\frac{1}{2}\left | \hat{E}_{2} \right |^{2}/\eta _{0}}{\frac{1}{2}\left | \hat{E}_{i} \right |^{2}/\eta _{0}}=\frac{\left | \hat{E}_{2} \right |^{2}}{\left | \hat{E}_{i} \right |^{2}}=\left ( \frac{24}{25} \right )^{2}\approx 0.92 \nonumber \]

Esta relación se puede aumentar a la unidad aplicando un recubrimiento dieléctrico de un cuarto de longitud de onda de espesor con índice de refracción\(n_{coating}=\sqrt{n}\), como se desarrolló en el Ejemplo 7-1. Esto no suele hacerse porque la relación en (14) ya es grande sin el gasto de un recubrimiento.

Fibra Óptica

(a) Tubo recto de luz

Las fibras largas hin de material transparente pueden guiar la luz a lo largo de una trayectoria recta si la luz dentro de la tubería incide sobre la pared en un ángulo mayor que el ángulo crítico\(\left ( \sin \theta _{c} \right )=1/n\):

\[\sin \theta _{2}=\cos \theta _{t}\geq \sin \theta _{c} \nonumber \]

Los rayos de luz son entonces totalmente reflejados internamente siendo confinados a la tubería hasta que salen, como en la Figura 7-26. El

Figura 7-26 El índice de refracción de una tubería de luz recta debe ser mayor que\(\sqrt{2}\) para las reflexiones internas totales de la luz incidente en cualquier ángulo.

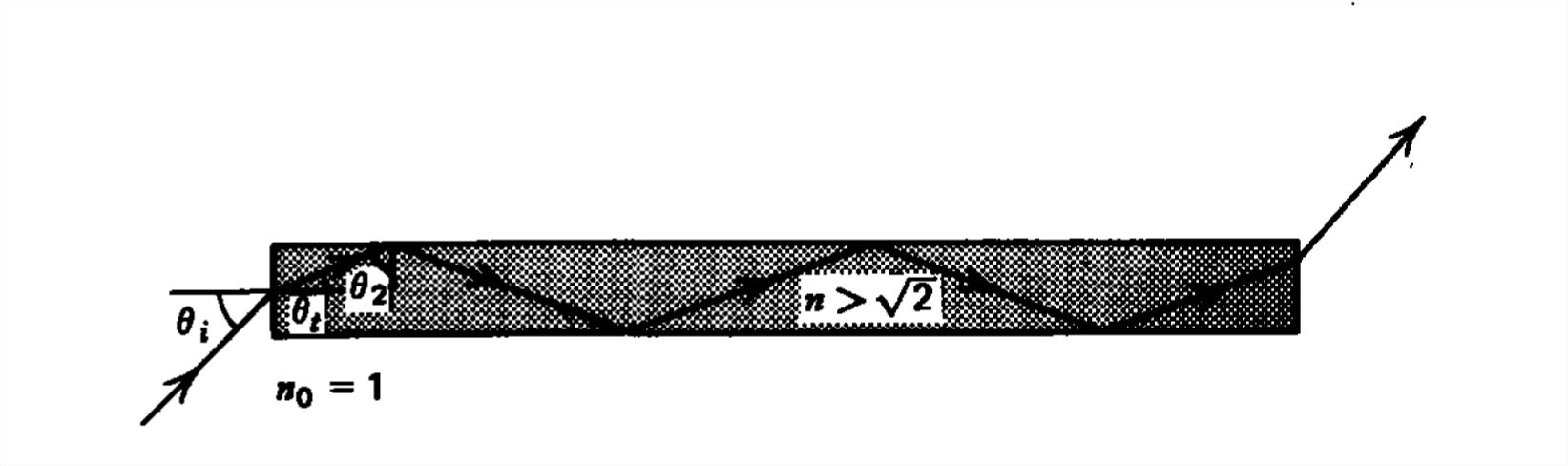
ángulo incidente está relacionado con el ángulo transmitido de la ley de Snell,

\[ \sin \theta _{t}=\left ( 1/n \right )\sin \theta _{i} \nonumber \]

de manera que (15) se convierte

\[ \cos\theta _{t}=\sqrt{1-\sin^{2} \theta _{t}}=\sqrt{1-\left ( 1/n^{2} \right )\sin^{2} \theta _{i}}\geq 1/n \nonumber \]

que cuando se resuelve para\(n\) rendimientos

\[ n^{2}\geq 1+\sin^{2} \theta _{i} \nonumber \]

Si se cumple esta condición por incidencia de pastoreo\(\left ( \theta _{i}=\pi /2 \right )\), toda la luz incidente pasará por la tubería, lo que requiere que

\[ n^{2}\geq 2\Rightarrow n\geq \sqrt{2} \nonumber \]

La mayoría de los tipos de vidrio tienen\(n\approx 1.5\) por lo que esta condición se cumple fácilmente.

(b) Fibras Dobladas

La luz también puede guiarse a lo largo de un camino tortuoso si la fibra está doblada, como en la tubería semicircular que se muestra en la Figura 7-27. El ángulo mínimo con la normal radial para la luz incidente mostrada es en el punto\(A\). Este ángulo en términos del radio de la curva y el ancho de la tubería de luz debe exceder el ángulo crítico

\[ \sin \theta _{A}=\frac{R}{R+d}\geq \sin \theta _{c} \nonumber \]

Figura 7-27 La luz puede guiarse a lo largo de una fibra doblada circularmente si\(R/d> 1/\left ( n-1 \right )\) como entonces siempre hay reflexión interna total cada vez que la luz incide en las paredes.

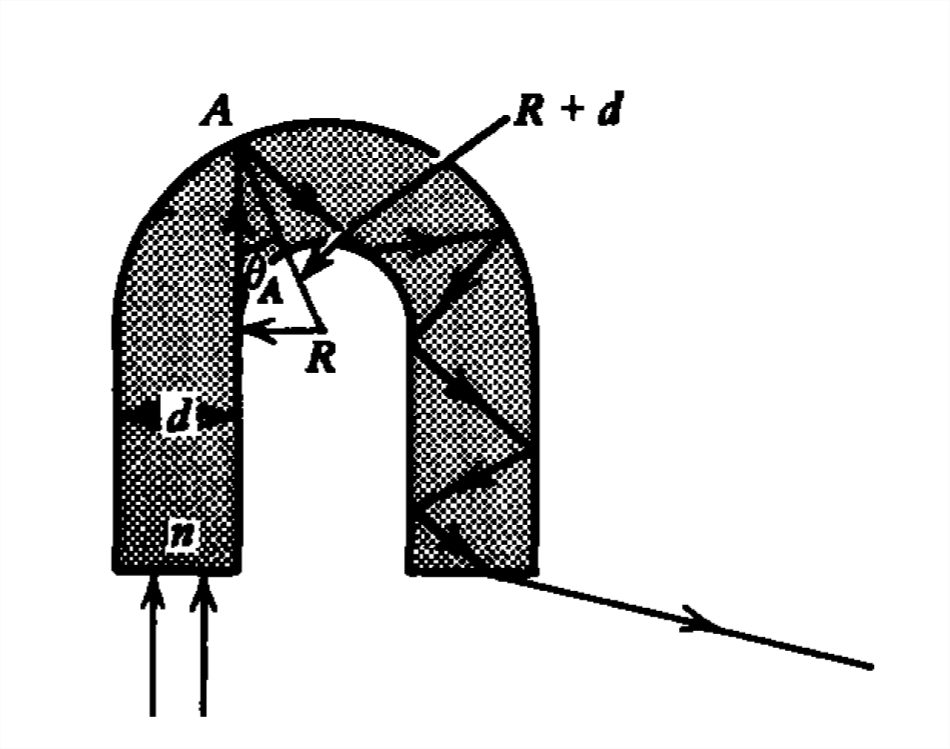
para que

\[ \frac{R/d}{R/d+1}\geq \frac{1}{n} \nonumber \]

que cuando se resuelve para\(R/d\) requiere

\[\frac{R}{d}\geq \frac{1}{n-1} \nonumber \]