8.3: Variaciones de tiempo sinusoidales

Soluciones a las Ecuaciones de Línea de Transmisión

A menudo, las líneas de transmisión son excitadas por fuentes que varían sinusoidalmente de modo que el voltaje y la corriente de la línea también varían sinusoidalmente con el tiempo:

\ [v\ izquierda (z, t\ derecha) =\ textrm {Re}\ izquierda [\ hat {v}\ izquierda (z\ derecha) e^ {j\ omega t}\ derecha]\
i\ izquierda (z, t\ derecha) =\ textrm {Re}\ izquierda [\ hat {i}\ izquierda (z\ derecha) e^ {j\ omega t}\ derecha]\ umber\]

Entonces como encontramos para las ondas TEM en la Sección 7-4, el voltaje y la corriente se encuentran a partir de las soluciones de ecuación de onda de la Sección 8-1-5 como combinaciones lineales de funciones exponenciales con argumentos\(t-z/c\) y\(t+z/c\):

\ [v\ izquierda (z, t\ derecha) =\ textrm {Re}\ izquierda [\ hat {\ textrm {V}} _ {+} e^ {j\ omega\ izquierda (t-z/c\ derecha)} +\ hat {\ textrm {V}} _ {-} e^ {j\ omega\ izquierda (t+z/c\ derecha)}\ derecha]\
i\ izquierda (z, t\ derecha) =Y_ {0}\ textrm {Re}\ izquierda [\ sombrero {\ textrm {V}} _ {+} e^ {j\ omega\ izquierda (t-z/c\ derecha)} -\ sombrero {\ textrm {V}} _ {-} e^ {j\ omega\ izquierda (t+z/c\ derecha)}\ derecha]\ nonumber\]

Ahora las amplitudes fásticas\(\hat{\textrm{V}}_{+}\) y\(\hat{\textrm{V}}_{-}\) son números complejos y no dependen de\(z\) ni\(t\).

Al factorizar la dependencia sinusoidal del tiempo en (2), las dependencias espaciales de la tensión y la corriente son

\ [\ hat {v}\ izquierda (z\ derecha) =\ hat {\ textrm {V}} _ {+} e^ {-jkz} +\ hat {\ textrm {V}} _ {-} e^ {+jkz}\
\ hat {i}\ left (z\ right) =Y_ {0}\ left (\ hat {\ textrm {V} _ {+} e^ {-jkz} -\ sombrero {\ textrm {V}} _ {-} e^ {+jkz}\ derecha)\ nonumber\]

donde el número de onda se define de nuevo como

\[ k=\omega /c \nonumber \]

Terminaciones sin pérdidas

(a) Línea cortocircuitada

La línea de transmisión mostrada en la Figura 8-15a es excitada por una fuente de voltaje sinusoidal al\(z = -l\) imponer la condición límite

\ [\ begin {align} v\ left (z=-l, t\ right) &=V_ {0}\ cos\ omega t\ nonumber\\ &
=\ textrm {Re}\ izquierda (V_ {0} e^ {j\ omega t}\ derecha)\ Rightarrow\ hat {v}\ left (z=-l\ right) =V_ {0} =\ hat {\ textrm {V}} _ {+} e^ {jkl} +\ hat {\ textrm {V}} _ {-} e^ {-jkl}\ end {align}\ nonumber\]

Tenga en cuenta que para usar (3) debemos escribir todas las sinusoides en notación compleja. Entonces como todas las variaciones de tiempo son de la forma\(e^{j\omega t}\), podemos suprimir escribirla cada vez y trabajar únicamente con las variaciones espaciales de (3).

Debido a que la línea de transmisión está cortocircuitada, tenemos la condición de límite adicional

\[ v\left ( z=0,t \right )=0\Rightarrow \hat{v}\left ( z=0 \right )=0=\hat{\textrm{V}}_{+}+\hat{\textrm{V}}_{-} \nonumber \]

que al resolverse simultáneamente con (5) rinde

\[ \hat{\textrm{V}}_{+}=-\hat{\textrm{V}}_{-}=\frac{V_{0}}{2j\sin kl} \nonumber \]

Las dependencias espaciales del voltaje y la corriente son entonces

\ [\ hat {v}\ izquierda (z\ derecha) =\ frac {V_ {0}\ izquierda (e^ {-jkz} -e^ {jkz}\ derecha)} {2j\ sin kl} =-\ frac {V_ {0}\ sin kz} {\ sin kl}\
\ sombrero {i}\ izquierda (z\ derecha) =\ frac {V_ {0} Y_ {0}\ izquierda (e^ {-jkz} +e^ {+jkz}\ derecha)} {2j\ sin kl} =-j\ frac {V_ {0} Y_ {0}\ cos kz} {\ sin kl}\ nonumber\]

El voltaje instantáneo y la corriente como funciones del espacio y el tiempo son entonces

\ [v\ izquierda (z, t\ derecha) =\ textrm {Re}\ izquierda [\ hat {v}\ izquierda (z\ derecha) e^ {j\ omega t}\ derecha] =-V_ {0}\ frac {\ sin kz} {\ sin kl}\ cos\ omega t\
i\ izquierda (z, t\ derecha) =\ textrm {Re}\ izquierda [\ hat {i}\ izquierda (z\ derecha) e^ {j\ omega t}\ derecha] =\ frac {V_ {0} Y_ {0}\ cos kz\ sin\ omega z} {\ sin kl}\ nonumber\]

Figura 8-15 Las distribuciones de voltaje y corriente en una (a) línea de transmisión cortocircuitada y (b) de circuito abierto excitada por fuentes de voltaje sinusoidales en\(z = -l\) Si las líneas son mucho más cortas que una longitud de onda, actúan como elementos de circuito reactivo. (c) A medida que se eleva la frecuencia, la impedancia reflejada en función de\(\) z puede parecer capacitiva o inductiva haciendo la transición a través de circuitos abiertos o cortocircuitos.

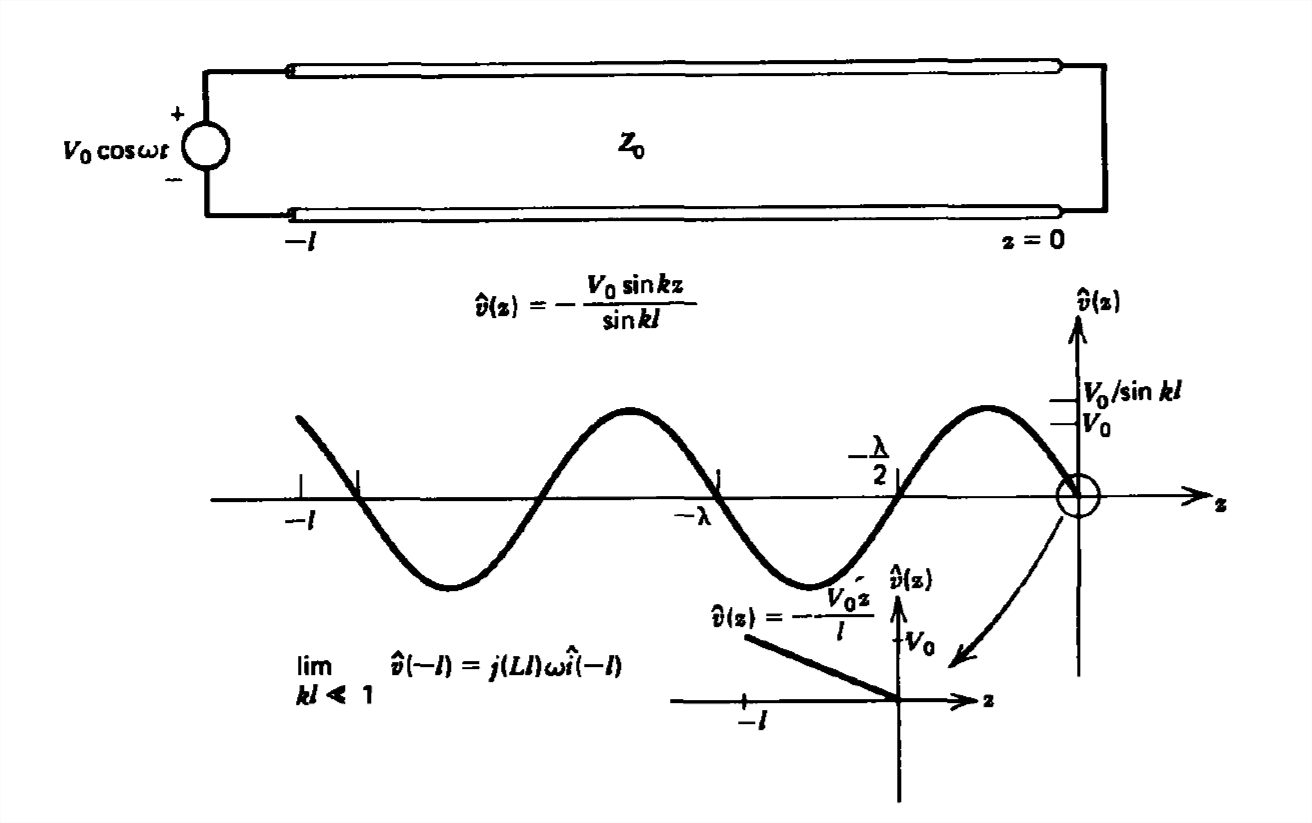
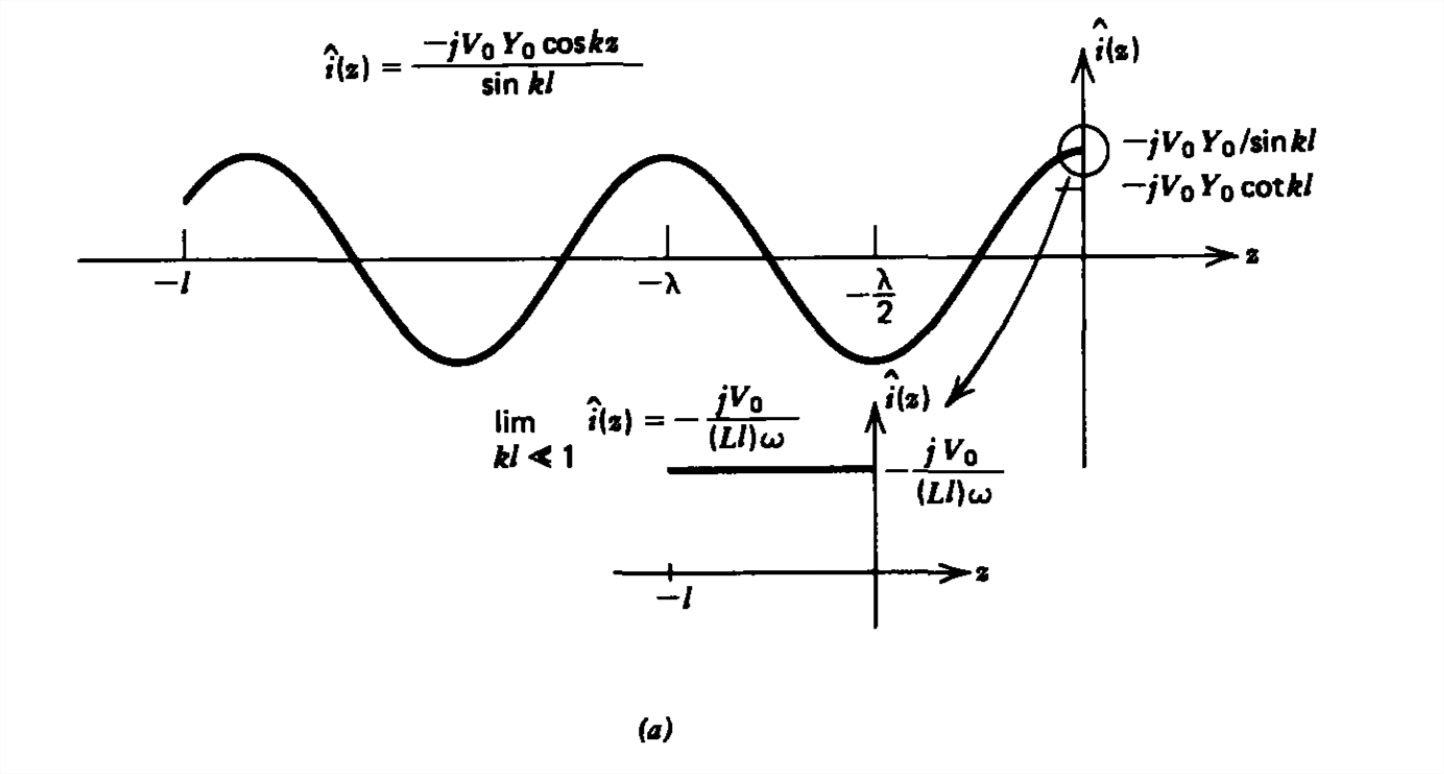
Las distribuciones espaciales de voltaje y corriente en función de\(z\) en un instante de tiempo específico se trazan en la Figura 8-15a y se ven\(90^{\circ }\) desfasadas entre sí en el espacio con sus distribuciones periódicas con longitud de onda\(\lambda \) dada por

\[ \lambda =\frac{2\pi }{k}=\frac{2\pi c}{\omega } \nonumber \]

La impedancia compleja en cualquier posición\(z\) se define como

\[ Z\left ( z \right )=\frac{\hat{v}\left ( z\right )}{\hat{i}\left ( z\right )} \nonumber \]

que para este caso especial de una línea cortocircuitada se encuentra de (8) como

\[ Z\left ( z \right )=-jZ_{0}\tan kz \nonumber \]

En particular, at\(z= -l\), la línea de transmisión aparece al generador como una impedancia de valor

\[ Z\left ( z=-l \right )=jZ_{0}\tan kz \nonumber \]

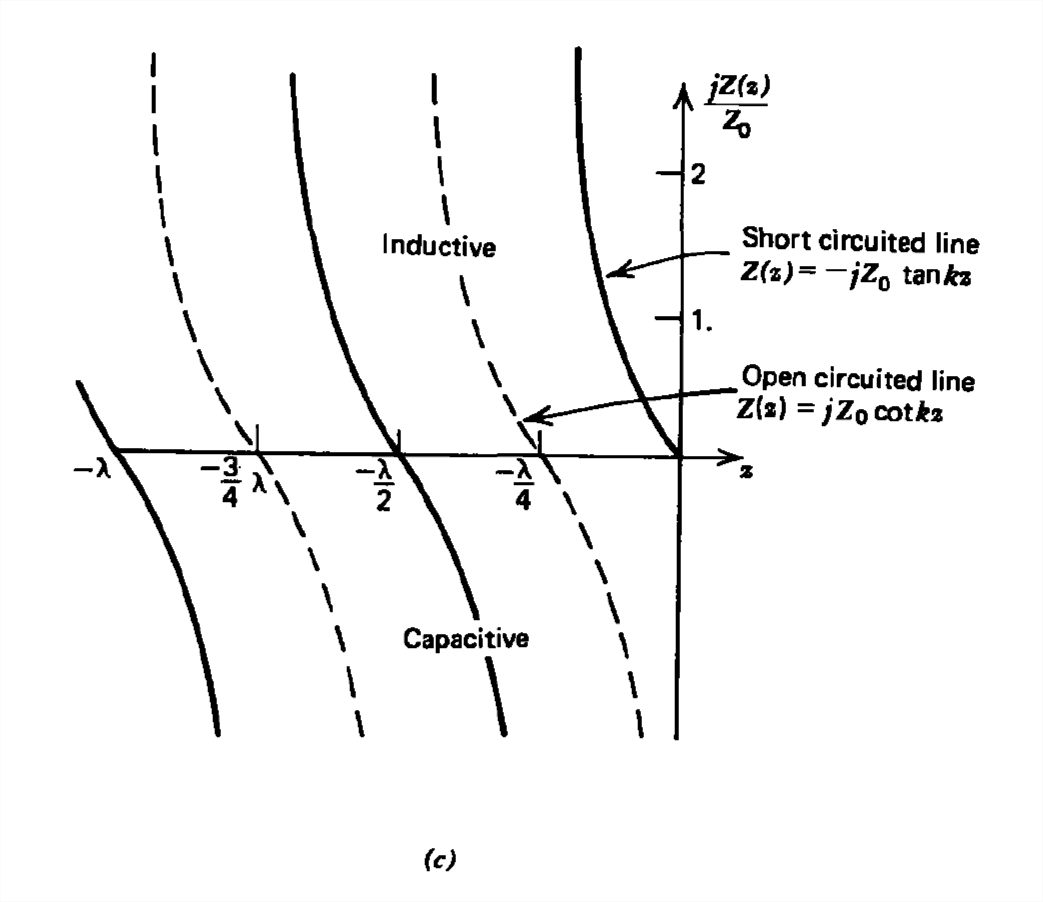
A partir de las líneas continuas de la Figura 8-15c vemos que existen diversos regímenes de interés:

1. Cuando la línea es un múltiplo entero de una longitud de onda media larga de modo que\(kl=n\pi ,\,n=1,2,3,...\), la impedancia a\(z= -l\) es cero y la línea de transmisión parece un cortocircuito.
2. Cuando la línea es un múltiplo entero impar de un cuarto de longitud de onda de modo que\(kl=\left ( 2n-1 \right )\pi/2 ,\,n=1,2,...\), la impedancia a\(z = -l\) es infinita y la línea de transmisión parece un circuito abierto.
3. Entre los límites de cortocircuito y circuito abierto\(\left ( n-1 \right )\pi < kl< \left ( 2n-1 \right )\pi/2,\,n=1,2,3,...\),\(Z\left ( z=-l \right )\) tiene una reactancia positiva y por lo tanto parece un inductor.
4. Entre los límites de circuito abierto y cortocircuito\(\left ( n-\frac{1}{2} \right )\pi < kl< n\pi/2,\,n=1,2,...\),\(Z\left ( z=-l \right )\) tiene una reactancia negativa árida por lo que parece un condensador.

Así, la línea de transmisión cortocircuitada adquiere todos los valores reactivos, tanto positivos (inductivos) como negativos (capacitivos), incluyendo abiertos y cortocircuitos en función de\(kl\) Así, si se cambia la longitud de la línea\(l\) o la frecuencia, la impedancia de la línea de transmisión es cambiado.

Examinando (8) también notamos que si\(\sin kl=0,\,\left ( kl=n\pi ,\,n=1,2,... \right )\), el voltaje y la corriente se vuelven infinitos (en la práctica el voltaje y la corriente se vuelven grandes limitados solo por pérdidas). Bajo estas condiciones, se dice que el sistema es resonante con las frecuencias resonantes dadas por

\[ \omega _{n}=n\pi c/l,\quad n=1,2,3,... \nonumber \]

Cualquier fuente de voltaje aplicada a estas frecuencias dará como resultado tensiones y corrientes muy grandes en la línea.

(b) Línea de Circuito Abierto

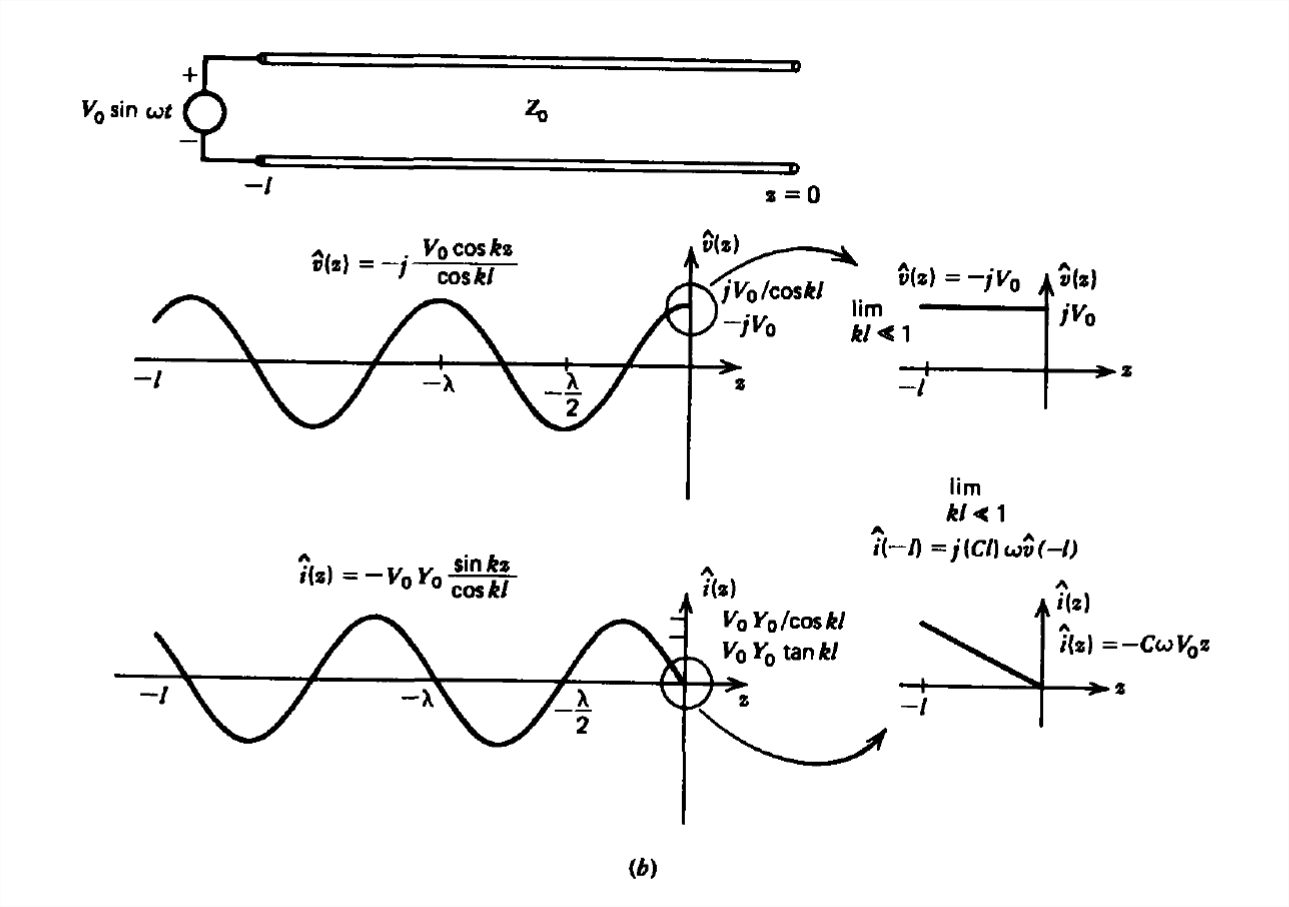
Si el cortocircuito es reemplazado por un circuito abierto, como en la Figura 8-15b, y por variedad cambiamos la fuente\(z = -l\) a\(V_{0}\sin \omega t\) las condiciones de límite son

\ [i\ izquierda (z=0, t\ derecha) =0\\
v\ izquierda (z=-l, t\ derecha) =V_ {0}\ sin\ omega t=\ textrm {Re}\ izquierda (-jV_ {0} e^ {j\ omega t}\ derecha)\ nonumber\]

Usando (3) las amplitudes complejas obedecen las relaciones

\ [\ hat {i}\ izquierda (z=0\ derecha) =0=Y_ {0}\ izquierda (\ textrm {V} _ {+} -\ textrm {V} _ _ {-}\ derecha)\
\ sombrero {v}\ izquierda (z=-l\ derecha) =-Jv_ {0} =\ textrm {V} _ _ {+} e^ {j^ kl} +\ textrm {V} _ _ {-} e^ {-jkl}\ nonumber\]

que cuenta con soluciones

\[ \hat{\textrm{V}}_{+}=\hat{\textrm{V}}_{-}=\frac{-jV_{0}}{2\cos kl} \nonumber \]

Las dependencias espaciales del voltaje y la corriente son entonces

\ [\ hat {v}\ izquierda (z\ derecha) =\ frac {-jv_ {0}} {2\ cos kl}\ izquierda (e^ {-jkz} +e^ {jkz}\ derecha) =\ frac {-jv_ {0}} {\ cos kl}\ cos kz\
\ sombrero {\ imath}\ izquierda (\ z derecha) =\ frac {-jV_ {0} Y_ {0}} {2\ cos kl}\ izquierda (e^ {-jkz} -e^ {+jkz}\ derecha) =-\ frac {V_ {0} Y_ {0}} {\ cos kl}\ sin kz\ nonumber\]

con soluciones instantáneas en función del espacio y el tiempo:

\ [v\ izquierda (z, t\ derecha) =\ textrm {Re}\ izquierda [\ hat {v}\ izquierda (z\ derecha) e^ {j\ omega t}\ derecha] =\ frac {V_ {0}\ cos kz} {\ cos kl}\ sin\ omega t\
i\ izquierda (z, t\ derecha) =\ textrm {Re}\ izquierda [\ sombrero {\ imath}\ izquierda (z\ derecha) e^ {j\ omega t}\ derecha] =-\ frac {V_ {0} Y_ {0}} {\ cos kl}\ sin kz\ cos\ omega t\ nonumber\]

La impedancia a\(z = -l\) es

\[ Z\left ( z=-l \right )=\frac{\hat{v}\left ( -l \right )}{\hat{\imath }\left ( -l \right )}=-jZ_{0}\cot kl \nonumber \]

Nuevamente la impedancia es puramente reactiva, como lo muestran las líneas discontinuas en la Figura 8-15c, alternando signos cada cuarto de longitud de onda para que la carga de circuito abierto mire a la fuente de voltaje como inductor, condensador, cortocircuito o circuito abierto dependiendo de la frecuencia y longitud de la línea.

La resonancia ocurrirá si

\[ \cos kl=0 \nonumber \]

o

\[ kl=\left ( 2n-1 \right )\pi /2,\quad n=1,2,3,... \nonumber \]

de modo que las frecuencias resonantes son

\[ \omega _{n}=\frac{\left ( 2n-1 \right )\pi c}{2l} \nonumber \]

Elementos de circuito reactivo como aproximaciones a líneas de transmisión cortas

Reexaminemos los resultados obtenidos para líneas cortas y de circuito abierto en el límite cuando\(l\) es mucho más corta que la longitud de onda\(\lambda \) para que en este límite de longitud de onda larga las funciones trigonométricas espaciales puedan aproximarse como

\ [\ lim_ {kl\ ll 1}\ izquierda\ {\ comenzar {matriz}
\ sin kz\ approx kz\
\ cos kz\ aprox 1
\ final {matriz}\ derecha. \ nonumber\]

Usando estas aproximaciones, el voltaje, la corriente y la impedancia para la línea cortocircuitada excitada por una fuente de voltaje se\(V_{0}\cos \omega t\) pueden obtener de (9) y (13) como

\ begin {align}\ lim_ {kl\ ll 1}\ left\ {\ begin {array} {lr}
v\ left (z, t\ right) =\ frac {V_ {0} z} {l}\ cos\ omega t,\ quad v\ izquierda (-l, t\ derecha) =V_ {0}\ cos\ omega t &\\
i\ izquierda (z, t\ derecha) =\ frac {V_ {0} Y_ {0}} {kl}\ sin\ omega t,\ quad i\ izquierda (-l, t\ derecha) =\ frac {V_ {0}\ sin\ omega t} {\ izquierda (Ll \ derecha)\ omega} &\\
Z\ izquierda (-l\ derecha) =jz_ {0} kl=j\ frac {\ omega Z_ {0} l} {c} =j\ omega\ izquierda (Ll\ derecha) &
\ end {array}\ derecha. \ end {align}

Vemos que la línea de transmisión cortocircuitada actúa como inductor de valor\(\left ( Ll \right )\) (recuerda que\(L\) es la inductancia por unidad de longitud), donde utilizamos las relaciones

\[ Z_{0}=\frac{1}{Y_{0}}=\sqrt{\frac{L}{C}},\quad c=\frac{1}{\sqrt{LC}} \nonumber \]

Tenga en cuenta que en\( z=-l\),

\[ v\left ( -l,t \right )=\left ( Ll \right )\frac{di\left ( -l,t \right )}{dt} \nonumber \]

De igual manera para la línea de circuito abierto obtenemos:

\ begin {align}\ lim_ {kl\ ll 1}\ izquierda\ {
\ begin {array} {lr}
v\ izquierda (z, t\ derecha) =V_ {0}\ sin\ omega t&\\
i\ izquierda (z, t\ derecha) =-V_ {0} Y_ {0} kz\ cos\ omega t&\\
Z\ izquierda (-l\ derecha) =\ frac {-jz_ {0}} {kl} =\ frac {-j} {\ izquierda (Cl\ derecha)\ omega} &
\ end {array}\ derecho. \ quad i\ izquierda (-l, t\ derecha) =\ izquierda (Cl\ derecha)\ omega V_ {0}\ cos\ omega t
\ end {align}

Para la línea de transmisión de circuito abierto, el voltaje y la corriente del terminal están simplemente relacionados como para un condensador,

\[ i\left ( -l,t \right )=\left ( Cl \right )\frac{dv\left ( -l,t \right )}{dt} \nonumber \]

con capacitancia dada por\(\left ( Cl \right )\).

En general, si la frecuencia de excitación es lo suficientemente baja como para que la longitud de una línea de transmisión sea mucho más corta que la longitud de onda, las aproximaciones del circuito de inductancia y capacitancia son apropiadas. No obstante, hay que recordar que si las frecuencias de interés son tan altas que la longitud de un elemento de circuito es comparable a la longitud de onda, ya no actúa como ese elemento. De hecho, como se encuentra en la Sección 8-3-2, un condensador puede incluso parecer un inductor, un cortocircuito o un circuito abierto a una frecuencia suficientemente alta mientras que viceversa un inductor también puede parecer capacitivo, un cortocircuito o un circuito abierto.

En general, si la terminación no es ni un cortocircuito ni un circuito abierto, la distribución de voltaje y corriente se involucra más para calcular y es objeto de la Sección 8-4.

Efectos de las pérdidas de línea

(a) Enfoque de Circuito Distribuido

Si las paredes dieléctricas y de la línea de transmisión tienen pérdidas óhmicas, las ondas de voltaje y corriente decaen a medida que se propagan. Debido a que las ecuaciones gobernantes de la Sección 8-1-3 son lineales con coeficientes constantes, en el estado estacionario sinusoidal asumimos soluciones de la forma

\ [v\ izquierda (z, t\ derecha) =\ textrm {Re}\ izquierda (\ hat {V} e^ {j\ izquierda (\ omega t-kz\ derecha)}\ derecha)\
i\ izquierda (z, t\ derecha) =\ textrm {Re}\ izquierda (\ hat {I} e^ {j\ izquierda (\ omega t-kz\ derecha)}\ derecha)\ umber\]

donde ahora\(\omega \) y no\(k\) se relacionan simplemente como la relación no dispersiva en (4). Más bien sustituimos (30) en la Ec. (28) en la Sección 8-1-3:

\ [\ frac {\ parcial i} {\ z parcial} =-C\ frac {\ v parcial} {\ t parcial} -Gv\ Rightarrow -jk\ hat {I} =-\ izquierda (Cj\ omega +G\ derecha)\ hat {V}\
\ frac {\ parcial v} {\ parcial z} =-L\ frac {\ parcial i} {\ t parcial} -IR\ Rightarrow -jk\ hat {V} =-\ izquierda (Lj\ omega +R\ derecha)\ sombrero {I}\ nonumber\]

lo que requiere que

\[ \frac{\hat{V}}{\hat{I}}=\frac{jk}{\left ( Cj\omega +G \right )}=\frac{Lj\omega +R}{jk} \nonumber \]

Resolvemos (32) de manera autoconsistente para\(k\) como

\[ k^{2}=-\left ( Lj\omega +R \right )\left ( Cj\omega +G \right )=LC\omega ^{2}-j\omega \left ( RC+LG \right )-RG \nonumber \]

El número de onda es así complejo para que encontremos las partes reales e imaginarias de (33) como

\ begin {align} k=k_ {r} +jk_ {i}\ fila derecha k_ {r} ^ {2} -k_ {i} ^ {2} &=LC\ omega ^ {2} -RG\ nonumber\\
2k_ {r} k_ {i} &=-\ omega\ izquierda (RC+LG\ derecha)\ end {align}

En el límite de baja pérdida donde\(\omega RC\ll 1\) y\(\omega LG\ll 1\), la desintegración espacial de\(k_i\) es pequeña en comparación con el número de onda de propagación\(k_r\). En este límite tenemos la siguiente solución aproximada:

\ begin {align}
\ lim_ {\ omega RC\ ll 1\\ omega LG\ ll 1}\ izquierda\ {\ begin {array}
k_ {r}\ approx\ pm\ omega\ sqrt {LC}\ pm\ omega /c &\\
k_ {i} =-\ frac {\ omega\ izquierda (RC+LG\ derecha)} {2k_ {r}} & aprox\ mp\ frac {1} {2}\ izquierda [R\ sqrt {\ frac {C} {L}} +G\ sqrt {\ frac {L} {C}}\ derecha]\\
&\ approx\ mp\ frac {1} {2}\ izquierda (RY_ {0} +GZ_ {0}\ derecha)
\ end {array}\ right. \ end {align}

Utilizamos el signo superior para las ondas que se propagan en la\(+z\) dirección y el signo inferior para las olas que viajan en la\(-z\) dirección.

b) Líneas sin distorsión

Usando el valor\(k\) de (33),

\[ k=\pm \left [ -\left ( Lj\omega +R \right )\left ( Cj\omega +G \right ) \right ]^{2} \nonumber \]

in (32) nos da la impedancia de onda dependiente de la frecuencia para las ondas que viajan en la\(\pm z\) dirección como

\[ \frac{\hat{V}}{\hat{I}}=\pm \left ( \frac{Lj\omega +R }{Cj\omega +G} \right )^{1/2}=\pm \sqrt{\frac{L}{C}}\left ( \frac{j\omega +R/L}{j\omega +G/C} \right )^{1/2} \nonumber \]

Si los parámetros de línea se ajustan de manera que

\[ \frac{R}{L}=\frac{G}{C} \nonumber \]

la impedancia en (37) se vuelve independiente de la frecuencia e igual a la impedancia de línea sin pérdidas. Bajo las condiciones de (38) el número de onda complejo se reduce a

\[ k_{r}=\pm \omega \sqrt{LC},\quad k_{i}=\mp \sqrt{RG} \nonumber \]

Aunque las ondas están atenuadas, todas las frecuencias se propagan a la misma velocidad de fase y grupo que para una línea sin pérdidas

\ [v_ {p} =\ frac {\ omega} {k_ {r}} =\ pm\ frac {1} {\ sqrt {LC}}\\
v_ {g} =\ frac {d\ omega} {dk_ {r}} =\ pm\ frac {1} {\ sqrt {LC}}\ nonumber\]

Dado que todos los componentes de Fourier de una excitación de pulso viajarán a la misma velocidad, la forma del pulso permanece sin cambios a medida que se propaga por la línea. Tales líneas se llaman sin distorsión.

c) Enfoque de campos

Si\(R = 0\), podemos encontrar directamente las soluciones de onda TEM utilizando las mismas soluciones que se encuentran para las ondas planas en la Sección 7-4-3. Allí encontramos que un dieléctrico con permitividad\(\varepsilon\) y pequeña conductividad óhmica\(\sigma \) tiene un número de onda complejo:

\[ \lim_{\sigma /\omega \varepsilon \ll 1}k\approx \left ( \frac{\omega }{c}-\frac{j\sigma \eta }{2} \right ) \nonumber \]

Equiparar (41) a (35) con lo\(R =0\) requiere\(GZ_{0}=\sigma \eta \).

El componente tangencial de\(\textbf{H}\) las paredes de la línea de transmisión perfectamente conductora es discontinuo por una corriente superficial. Sin embargo, si la pared tiene una conductividad óhmica grande pero no infinita\(\sigma _{w}\), los campos penetran con una distancia característica igual a la profundidad de la piel\(\delta =\sqrt{2/\omega \mu \sigma _{w}}\). La corriente\(z\) dirigida resultante da lugar a un campo eléctrico\(z\) -dirigido para que las ondas ya no sean puramente TEM.

Debido a que asumimos que esta pérdida es pequeña, podemos usar un método de perturbación aproximada para encontrar la tasa de desintegración espacial de los campos. Suponemos que los campos entre electrodos planos paralelos son esencialmente los mismos que cuando el sistema no tiene pérdidas excepto que ahora se atenúa exponencialmente como\(e^{-\alpha z}\), donde\(\alpha =-k_{i}\):

\ [\ begin {align} E_ {x}\ izquierda (z, t\ derecha) &=\ textrm {Re}\ izquierda [\ hat {E} e^ {j\ izquierda (\ omega t-k_ {r} z\ derecha)} e^ {-\ alpha z}\ derecha]\ nonumber\\
H_ {y}\ izquierda (z, t\ derecha) &=\ textrer m {Re}\ izquierda [\ frac {\ hat {E}} {\ eta} e^ {j\ izquierda (\ omega t-k_ {r} z\ derecha)} e^ {-\ alpha z}\ derecha],\ quad k_r=\ frac {\ omega } {c}\ end {align}\ nonumber\]

De la parte real del teorema complejo de Poynting derivado en la Sección 7-2-4, relacionamos la divergencia de la densidad de potencia electromagnética promedio en el tiempo con la potencia disipada promedio en el tiempo:

\[ \nabla \cdot <\textbf{S}>=-<P_{d}> \nonumber \]

Utilizando el teorema de divergencia integramos (43) sobre un volumen de espesor\(\Delta z\) que abarca todo el ancho y grosor de la línea, como se muestra en la Figura 8-16:

\ [\ begin {align}\ int_ {\ textrm {V}}\ nabla\ cdotd <\ textbf {S} >\ textrm {V} &=\ oint_ {\ textrm {\ textrm {S}} <\ textbf {S} >\ cdot\ textbf {dS}\ nonumber
\\ &=\ int_ {z+\ Delta z d\ <S_ {z}\ left (z+\ Delta z\ right) > textrm {S}\ noner\\ &\
quad\ int_ {z d\ textrm <S_ {z}\ left (z\ right) > {S} =- \ int_ {\ textrm {V}} <P_d>d\ textrm {V}\ final {alinear}\ nonumber\]

El poder\(<P_d>\) se disipa en el dieléctrico y en las paredes. Definición de la potencia electromagnética total como

\[ <P(z)>=\int_{z}<S_{z}\left ( z\right )>d\textrm{S} \nonumber \]

Figura 8-16 Una línea de transmisión con paredes con pérdida y dieléctrico da como resultado ondas que decaen a medida que se propagan. La tasa\(\alpha \) de desintegración espacial de los campos es aproximadamente proporcional a la relación entre la potencia disipada promedio en el tiempo por unidad de longitud\(<P_{dL}>\) y el flujo\(<P>\) de potencia electromagnética promedio en el tiempo total en la línea.

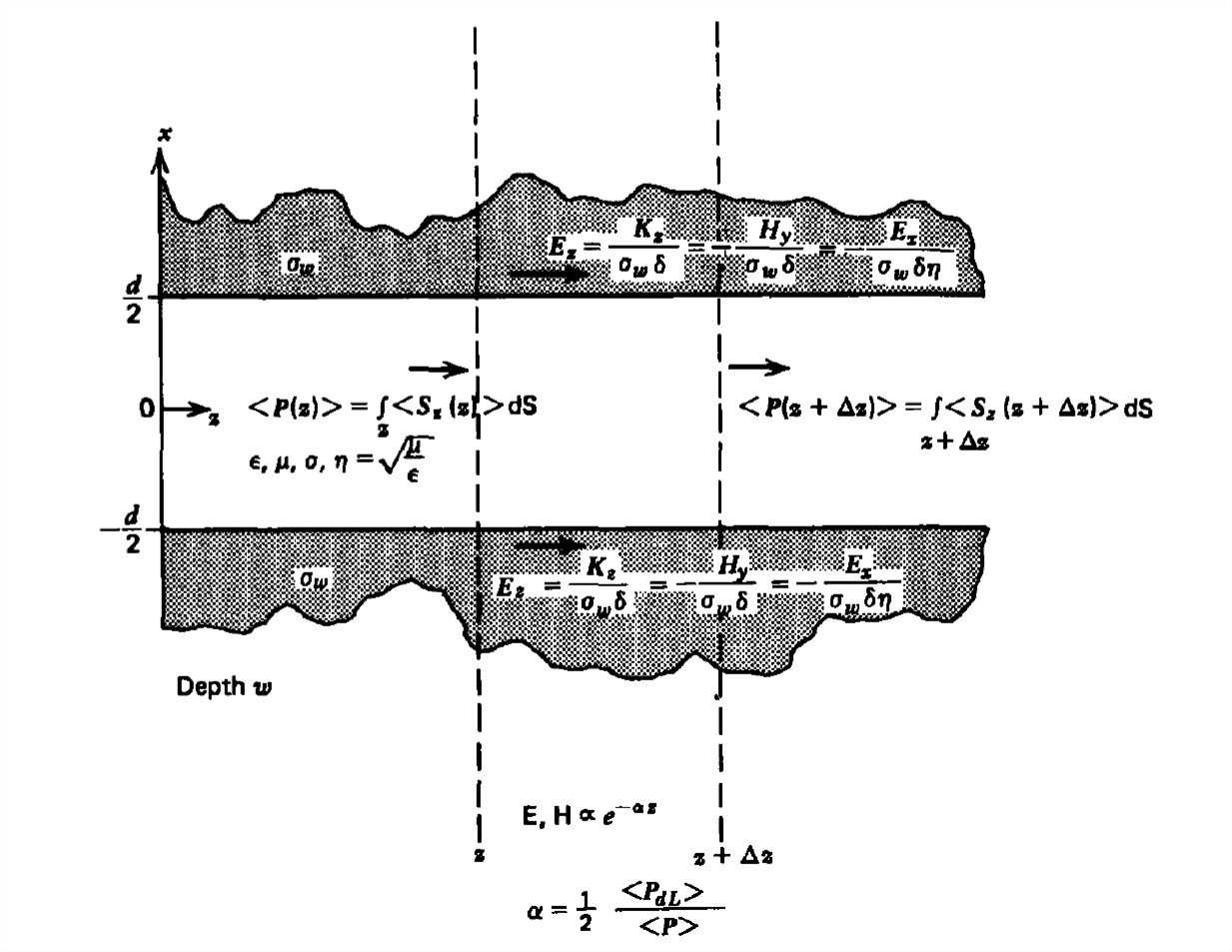
(44) se puede reescribir como

\[  <P(z+\Delta z)>- <P(z)>=-\int<P_{(d)}>dx\,dy\,dz \nonumber \]

Dividiendo por\(dz = \Delta z\), tenemos en el límite infinitesimal

\ [\ begin {align}\ lim_ {\ Delta z\ rightarrow 0}\ frac - <P (z+\ Delta z) > }<P (z) > {\ Delta z} &=\ frac {d }<P (z) > {dz} =-\ int_ {\ textrm {S} dx\ <P_ {d} >, dy\ nonumber\\ &=-\
end<P_ {dL} > {align}\ nonumber\]

donde\(<P_{dL}>\) se disipa la potencia por unidad de longitud. Dado que los campos varían como\(e^{-\alpha z}\), el flujo de potencia que es proporcional al cuadrado de los campos debe variar de\(e^{-2\alpha z}\) manera que

\[ \frac{d<P>}{dz}=-2\alpha <P>=-<P_{dL}> \nonumber \]

que cuando se resuelve para la tasa de desintegración espacial es proporcional a la relación entre la potencia disipada por unidad de longitud y la potencia electromagnética total que fluye por la línea de transmisión:

\[ \alpha =\frac{1}{2}\frac{<P_{dL}>}{<P>} \nonumber \]

Para nuestra línea de transmisión con pérdidas, la potencia se disipa tanto en las paredes como en el dieléctrico. Afortunadamente, no es necesario resolver el complicado problema de campo dentro de las paredes porque ya conocemos aproximadamente el campo magnético en las paredes de (42). Dado que la corriente de pared se limita efectivamente a la profundidad de la piel\(\delta \), el área de sección transversal a través de la cual fluye la corriente es esencialmente\(w\delta \) para que podamos definir la conductividad superficial como\(\sigma_{w}\delta \), donde el campo eléctrico en la pared está relacionado con la corriente superficial sin pérdidas como

\[ \textbf{K}_{w}=\sigma _{w}\delta \textbf{E}_{w} \nonumber \]

La corriente superficial en la pared se encuentra aproximadamente a partir del campo magnético en (42) como

\[ K_{z}=-H_{y}=-E_{x}/\eta  \nonumber \]

La potencia promedio en el tiempo disipada en la pared es entonces

\[ <P_{dL}>_{\textrm{wall}}=\frac{w}{2}\textrm{Re}\left ( \textbf{E}_{w}\cdot \textbf{K}_{w}^{\ast } \right )=\frac{1}{2}\frac{\left | \textbf{K}_{w} \right |^{2}w}{\sigma _{w}\delta }=\frac{1}{2}\frac{\left | \hat{E} \right |^{2}w}{\sigma _{w}\delta \eta ^{2}} \nonumber \]

La potencia disipada promedio en el tiempo total en las paredes y el dieléctrico por unidad de longitud para un sistema de línea de transmisión de profundidad\(w\) y espaciado de placas\(d\) es entonces

\ [\ begin {align &=2_ <P_ {dL} > {<P_ {dL} >\ textrm {wall}} +\ frac {1} {2}\ sigma\ izquierda |\ hat {E}\ derecha |^ {2} wd\ nonumber\\ & =\
frac {1} {2}\ izquierda |\ hat {E}\ derecha |^ {2} w\ izquierda (\ frac {2} {eta\ ^ {2}\ sigma _ {w}\ delta} +\ sigma d\ derecha)\ end {align}\ nonumber\]

donde multiplicamos (52) por dos debido a las pérdidas en ambos electrodos. La potencia electromagnética promedio en el tiempo es

\[ <P>=\frac{1}{2}\frac{\left | \hat{E} \right |^{2}}{\eta }wd \nonumber \]

para que la tasa de desintegración espacial se encuentre de (49) como

\[ \alpha =-k_{i}=\frac{1}{2}\left ( \frac{2}{\eta ^{2}\sigma _{w}\delta }+\sigma d \right )\frac{\eta }{d}=\frac{1}{2}\left ( \sigma \eta +\frac{2}{\eta \sigma _{w}\delta d}\right ) \nonumber \]

Comparando (55) con (35) vemos que

\ [GZ_ {0} =\ sigma\ eta,\ quad RY_ {0} =\ frac {2} {\ eta\ sigma _ {w}\ delta d}\
\ fila derecha Z_ {0} =\ frac {1} {Y_ {0}} =\ frac {d} {w}\ eta,\ quad G=\ frac {\ sigma w} {d},\ quad R=\ frac {2} {\ sigma _ {w} w\ delta}\ nonumber\]