8.5: Afinación de Stub
- Page ID
- 86908
En la práctica, la mayoría de las fuentes están conectadas a una línea de transmisión a través de una resistencia en serie coincidente con la línea Esto elimina las reflexiones transitorias cuando la excitación está encendida o apagada. Para maximizar el flujo de potencia a una carga, también es necesario que la impedancia de carga reflejada de nuevo a la fuente sea igual a la impedancia de la fuente y por lo tanto igual a la impedancia característica de la línea,\(Z_{0}\). Esta coincidencia de la carga con la línea para una terminación arbitraria solo se puede realizar agregando elementos adicionales a lo largo de la línea.
Por lo general, estos elementos son líneas de transmisión cortocircuitadas, llamadas stubs, cuyas longitudes pueden ser variadas. La reactancia del trozo se puede cambiar en el rango de\(-j\infty \) a\(j\infty\) simplemente variando su longitud, como se encuentra en la Sección 8-3-2, para la línea cortocircuitada. Debido a que los talones suelen estar conectados en paralelo a una línea de transmisión, es más conveniente trabajar con admisiones en lugar de impedancias ya que las admisiones en paralelo simplemente agregan.
Uso de la Gráfica Smith para Cálculos de Admisiones
Afortunadamente, el gráfico Smith también se puede usar directamente para cálculos de admisión donde la admisión normalizada se define como
\[ Y_{n}\left ( z \right )=\frac{Y\left ( z \right )}{Y_{0}}=\frac{1}{Z_{n}\left ( z \right )} \nonumber \]
Si\(Y_{nL}\) se conoce la admitancia de carga normalizada, los cálculos de impedancia directos primero requieren el cálculo
\[ Z_{nL}=1/Y_{nL} \nonumber \]
para que pudiéramos entrar en la tabla de Smith en\(Z_{nL}\). Después giramos por el ángulo requerido correspondiente\(2kz\) y leemos el nuevo\(Z_{n}\left ( z \right )\). Luego nuevamente calculamos su recíproco para encontrar
\[ Y_{n}\left ( z \right )=1/Z_{n}\left ( z \right ) \nonumber \]
Las dos operaciones de tomar lo recíproco son tediosas. Podemos usar el propio gráfico Smith para invertir la impedancia utilizando el hecho de que la impedancia normalizada se invierte por una\(\lambda /4\) sección de línea, de modo que una rotación de\(\Gamma \left ( z \right )\) por\(180^{\circ }\) cambia una impedancia normalizada en su recíproco. De ahí que si se da la admisión, ingresamos al gráfico de Smith con un valor dado de admitancia normalizada\(Y_{n}\) y rotamos por\(180^{\circ }\) para encontrar\(Z_{n}\). Luego giramos por el número apropiado de longitudes de onda para encontrar\(Z_{n}\left ( z \right )\). Por último, volvemos a rotar\(180^{\circ }\) para encontrar\(Y_{n}\left ( z \right )=1/Z_{n}\left ( z \right )\). De hecho, hemos girado el coeficiente de reflexión por un ángulo de\(2\pi +2kz\). La rotación por\(2\pi\) en el gráfico de Smith, sin embargo, nos lleva de vuelta a donde empezamos, de manera que solo la\(2kz\) rotación es significativa. Siempre y cuando hagamos un número par de\(\pi\) rotaciones ingresando al gráfico de Smith con una admisión y saliendo nuevamente con una admisión, podemos usar el gráfico de Smith con admisiones normalizadas exactamente como si fueran impedancias normalizadas.
La impedancia de carga en una\(50\)\(\textrm{Ohm}\) línea es
\[ Z_{L}=50\left ( 1+j \right ) \nonumber \]
¿Cuál es la admisión de la carga?
SOLUCIÓN
Por cómputo directo tenemos
\[ Y_{L}=\frac{1}{Z_{L}}=\frac{1}{50\left ( 1+j \right )}=\frac{\left ( 1-j \right )}{100}\nonumber \]
Para utilizar la gráfica Smith encontramos la impedancia normalizada\(A\) en la Figura 8-23:
\[ Z_{nL}=1+j \nonumber \]
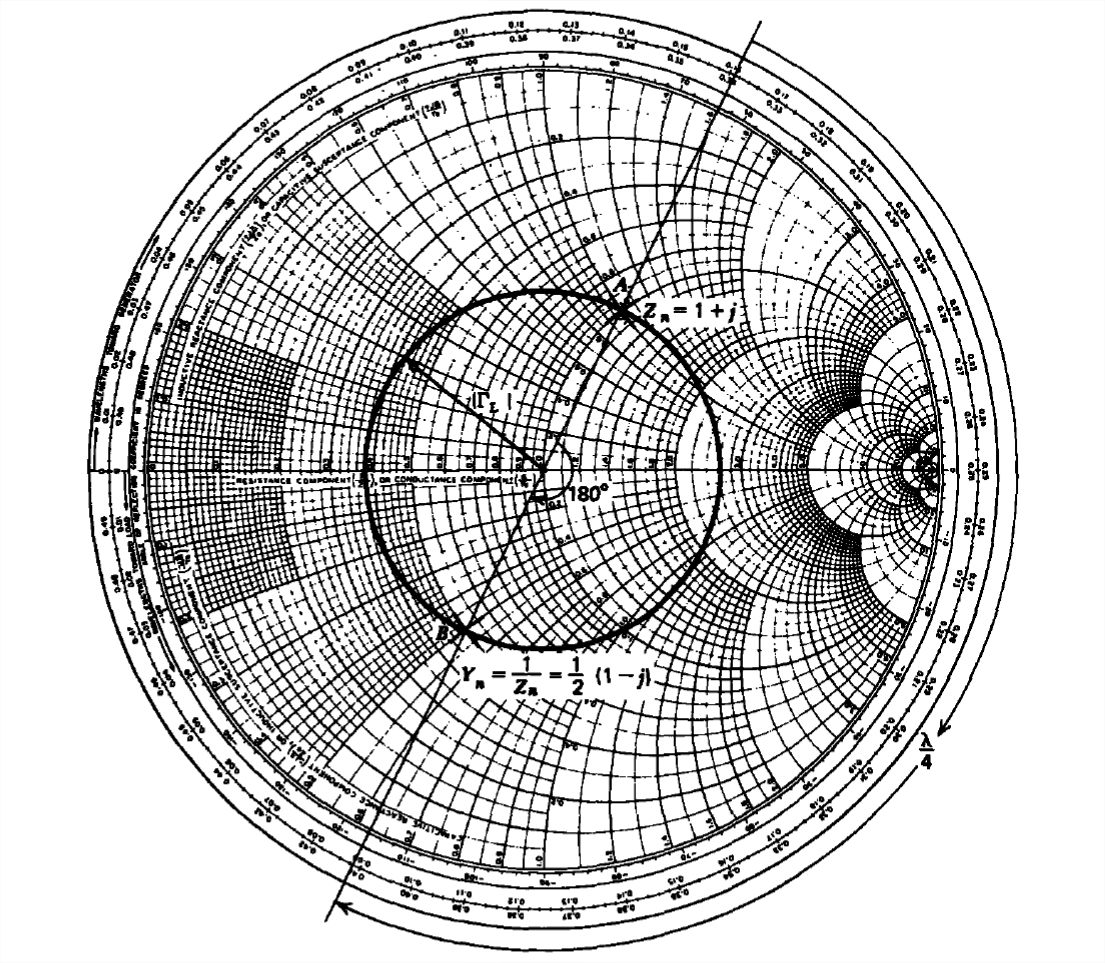
La admitancia normalizada que es el recíproco de la impedancia normalizada se encuentra ubicando la impedancia a una\(\lambda /4\) distancia del extremo de carga en\(B\):
\[ Y_{nL}=0.5\left ( 1-j \right )\Rightarrow Y_{L}=Y_{n}Y_{0}=\left ( 1-j \right )/100 \nonumber \]
Tenga en cuenta que el punto\(B\) está justo\(180^{\circ }\) lejos de\(A\) en el\(\left | \Gamma _{L} \right |\) círculo constante. Para cargas más complicadas el gráfico Smith es una manera conveniente de encontrar el recíproco de un número complejo.
Coincidencia de un solo trozo
Una terminación del valor\(Z_{L}=50\left ( 1+j \right )\) en una\(50\) línea de\(\textrm{Ohm}\) transmisión debe ser emparejada por medio de un trozo cortocircuitado a una distancia L de la carga, como se muestra en la Figura 8-24a. Necesitamos encontrar la longitud de la línea\(l_{1}\) y la longitud del trozo de\(l_{2}\) tal manera que la impedancia en la unión se corresponda con la línea\(\left ( Z_{in}=50\,\textrm{Ohm} \right )\). Entonces sabemos que todos los puntos posteriores a la izquierda de la unión tienen la misma impedancia de\(50\,\textrm{Ohms}\).
Debido a la conexión paralela, es más sencillo utilizar el gráfico Smith como transformación de admisión. La admitancia de carga normalizada se puede calcular usando el gráfico Smith rotando\(180^{\circ }\) desde la impedancia de carga normalizada a\(A\), como se muestra en la Figura 8-23 y Ejemplo 8-3,
\[ Z_{nL}=1+j \nonumber \]
para rendir
\[ Y_{nL}=0.5\left ( 1-j \right ) \nonumber \]
en el punto\(B\).
Ahora sabemos por la Sección 8-3-2 que el trozo cortocircuitado sólo puede agregar un componente imaginario a la admisión. Ya que queremos que la admisión total normalizada sea la unidad a la izquierda del talón en la Figura 8-24
\[ Y_{in}=Y_{1}+Y_{2}=1 \nonumber \]
cuando\(Y_{nL}\) se refleja de nuevo a\(Y_{1}\) ser debe terminar en el círculo cuya parte real es\(1\) (como solo\(Y_{2}\) puede ser imaginario), lo que ocurre ya sea en\(C\) o atrás\(l_{1}\) al\(A\) permitir estar\(0.25\lambda \) en\(A\) o\(\left (0.25 +0.177 \right )\lambda =0.427\lambda \) en\(C\) (o estos más cualquier múltiplo entero de\(\lambda /2\)). Entonces\(Y_{1}\) es cualquiera de los siguientes dos valores conjugados:
\ [Y_ {1} =\ izquierda\ {\ comenzar {matriz}
1+j,\ quad l_ {1} =0.25\ lambda\,\ izquierda (A\ derecha)\\
1-j,\ quad l_ {1} =0.427\ lambda\,\ izquierda (C\ derecha)
\ end {matriz}\ derecha. \ nonumber\]
\(Y_{in}\)Para que sea unidad debemos escoger\(Y_{2}\) tener una parte imaginaria para simplemente cancelar la parte imaginaria de\(Y_{1}\):
\ [Y_ {2} =\ izquierda\ {\ comenzar {matriz}
-j,\ quad l_ {1} =0.25\ lambda\
+j,\ quad l_ {1} =0.427\ lambda
\ end {matriz}\ derecha. \ nonumber\]
lo que significa, ya que el extremo cortocircuitado tiene una admitancia infinita en\(D\) que el stub debe ser de longitud tal como para rotar la admitancia a los puntos\(E\) o\(F\) requerir una longitud stub\(l_{2}\) de\(\left ( \lambda /8 \right )\left ( E \right )\) o\(\left ( 3\lambda /8 \right )\left ( F \right )\) (o estos valores más cualquier múltiplo entero de\(\lambda /2\)). Así, las soluciones se pueden resumir como
\[ l_{1}=0.25\lambda +n\lambda /2,\quad l_{2}=\lambda /8+m\lambda /2 \nonumber \]
o
\[ l_{1}=0.427\lambda +n\lambda /2,\quad l_{2}=3\lambda /8+m\lambda /2 \nonumber \]
donde\(n\) y\(m\) son cualquier número entero no negativo (incluyendo cero).
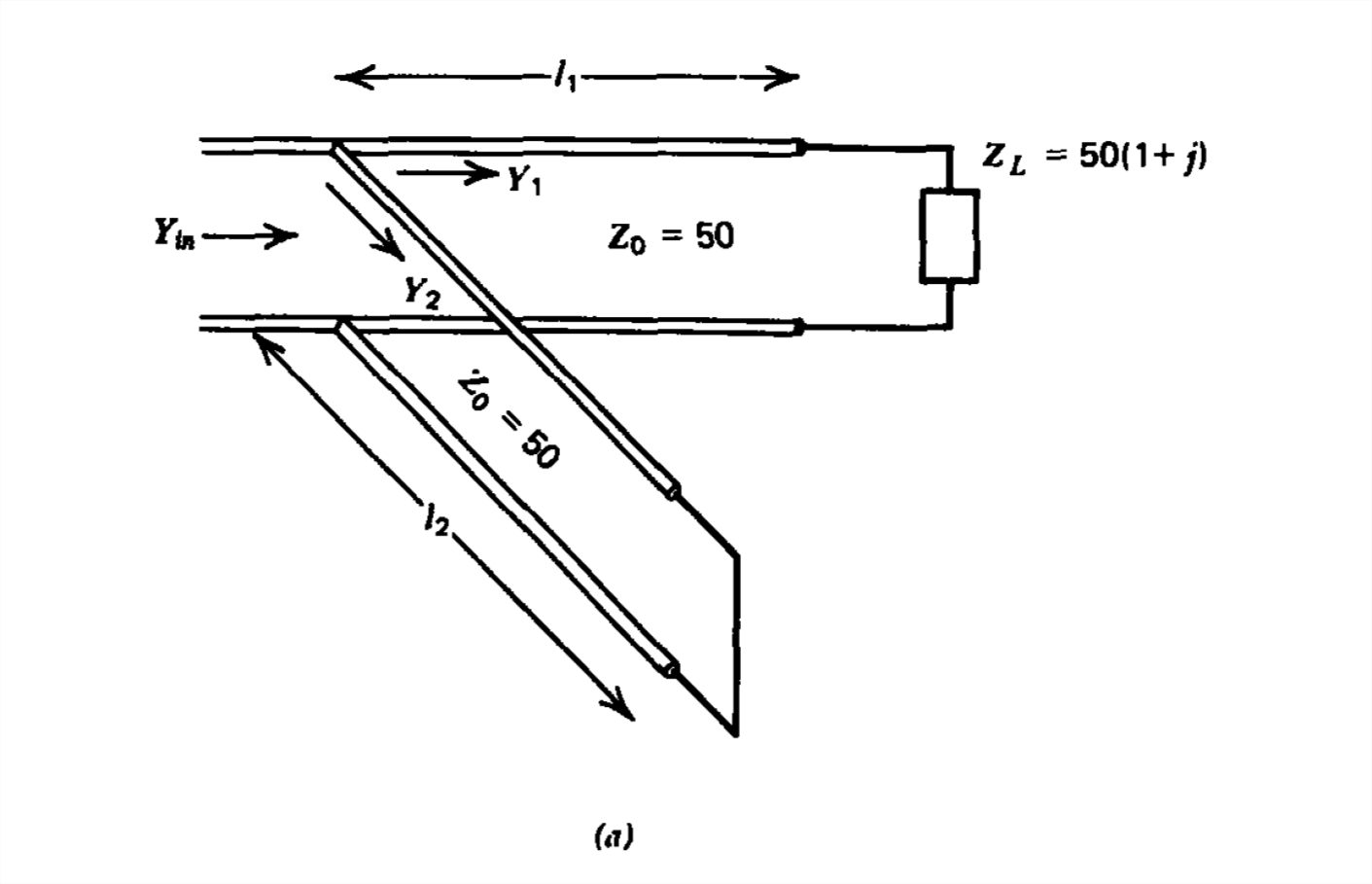
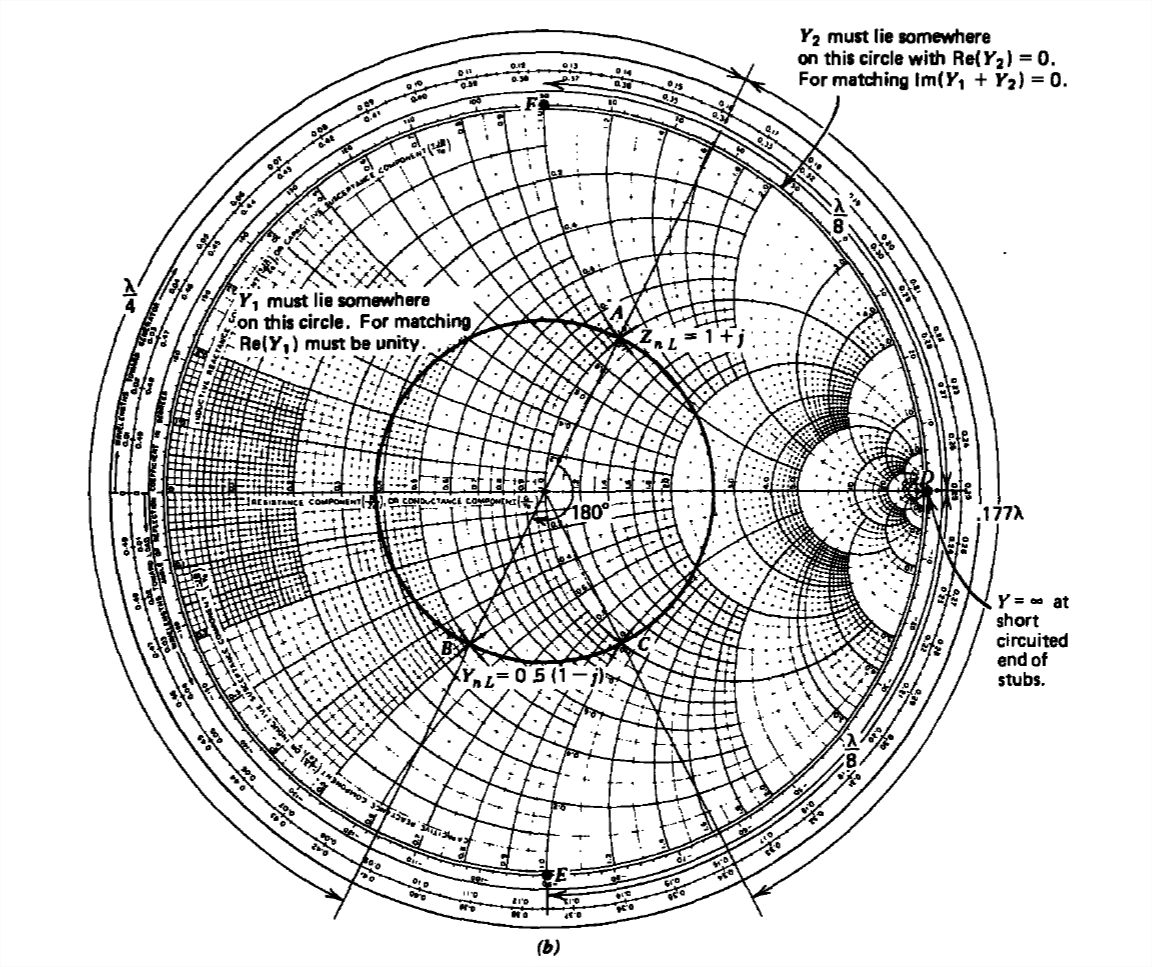
Figura 8-24 (a) Un sintonizador de un solo trozo que consiste en una línea cortocircuitada de longitud variable\(l_{2}\) puede hacer coincidir cualquier carga con la línea colocando el trozo a la distancia apropiada\(l_{1}\), de la carga. b) Construcción de gráficos Smith. (c) Patrón de onda estacionaria de voltaje.
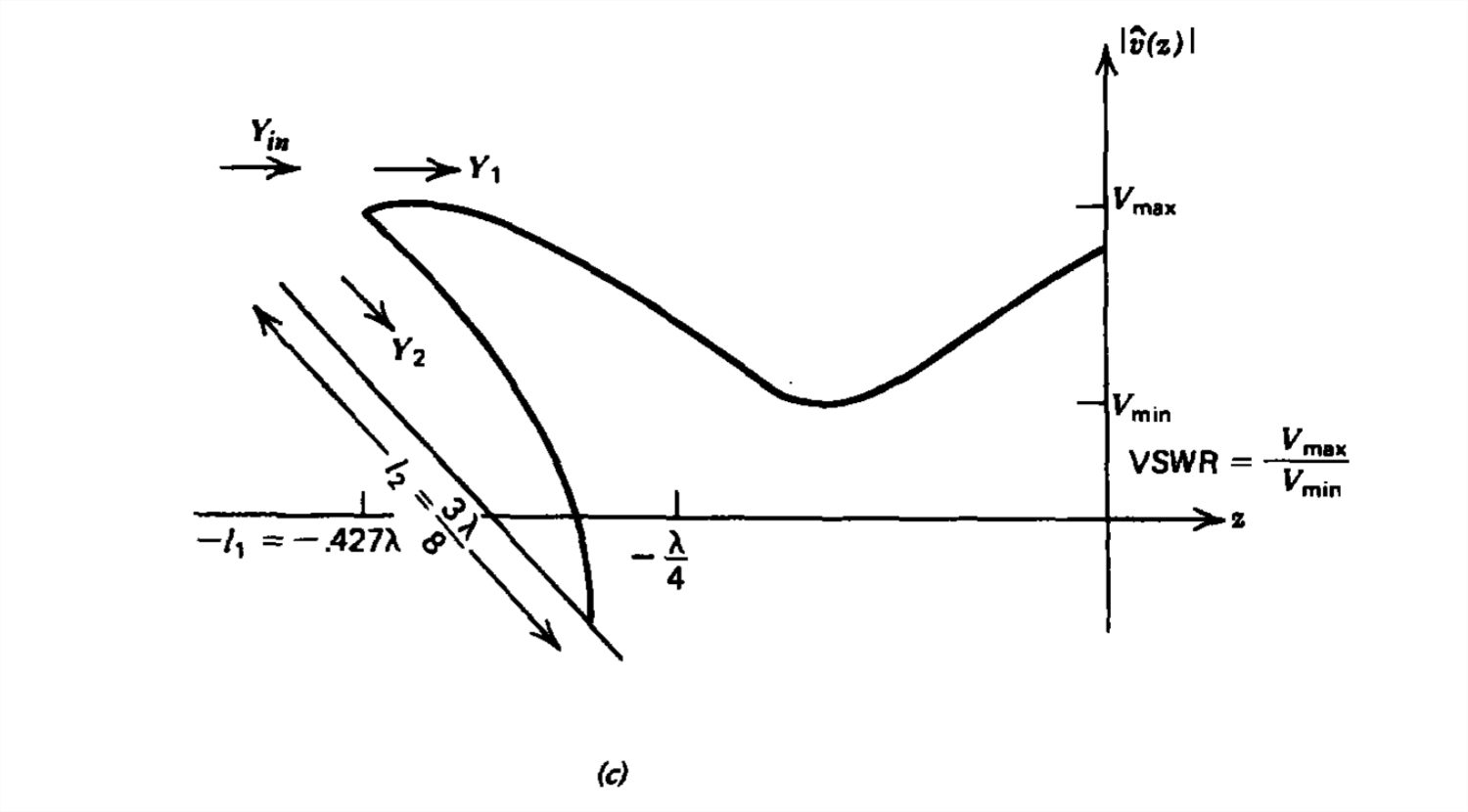
Cuando la carga es igualada por el trozo a la línea, la\(\textrm{VSWR}\) a la izquierda del trozo es la unidad, mientras que a la derecha del trozo sobre la longitud\( l_{1}\) el coeficiente de reflexión es
\[ \Gamma _{L}=\frac{Z_{nL}-1}{Z_{nL}+1}=\frac{j}{2+j} \nonumber \]
que tiene magnitud
\[ \left |\Gamma _{L} \right |=1/\sqrt{5}\approx 0.447 \nonumber \]
para que la relación de onda estacionaria de voltaje sea
\[ \textrm{VSWR}=\frac{1+\left |\Gamma _{L} \right |}{1-\left |\Gamma _{L} \right |}\approx 2.62 \nonumber \]
La desventaja de la afinación de un solo trozo es que no es fácil variar la longitud\( l_{1}\). Generalmente, los nuevos elementos solo se pueden conectar en los extremos de la línea y no entre ellos.
Coincidencia de Doble Stub
Esta dificultad de no tener una línea de longitud variable se puede superar mediante el uso de dos talones cortocircuitos separados de longitud fija, como se muestra en la Figura 8-25a. Esta longitud fija suele ser\(\frac{3}{8}\lambda \). Se hace una coincidencia ajustando la longitud de los talones\( l_{1}\) y
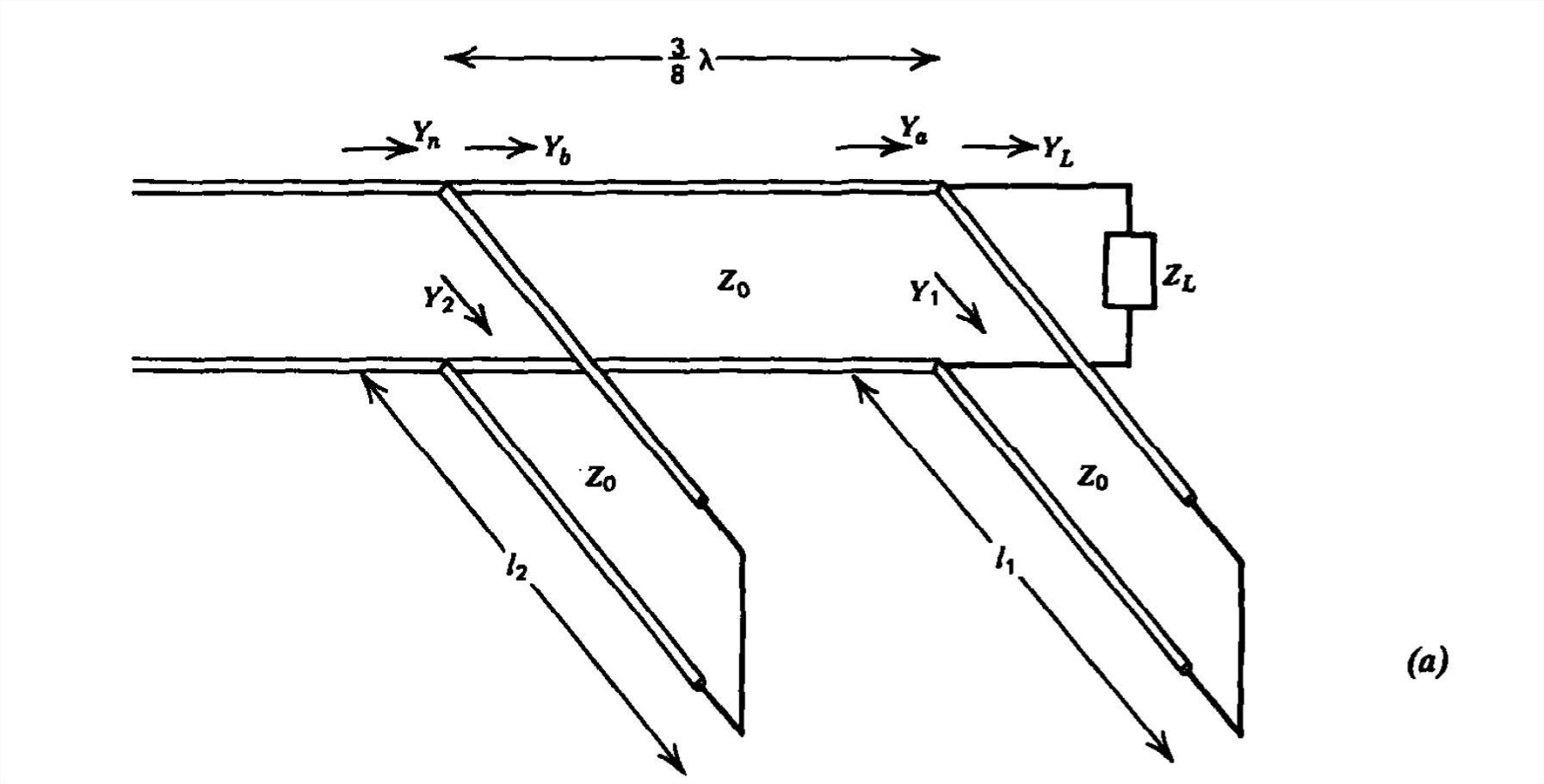
\\( l_{2}\). Un problema con el afinador de doble tetón es que no todas las cargas se pueden igualar para un espaciado de stub dado.
Las admisiones normalizadas en cada cruce se relacionan como
\ [Y_ {a} =Y_ {1} +Y_ {L}\\
Y_ {n} =Y_ {2} +Y_ {b}\ nonumber\]
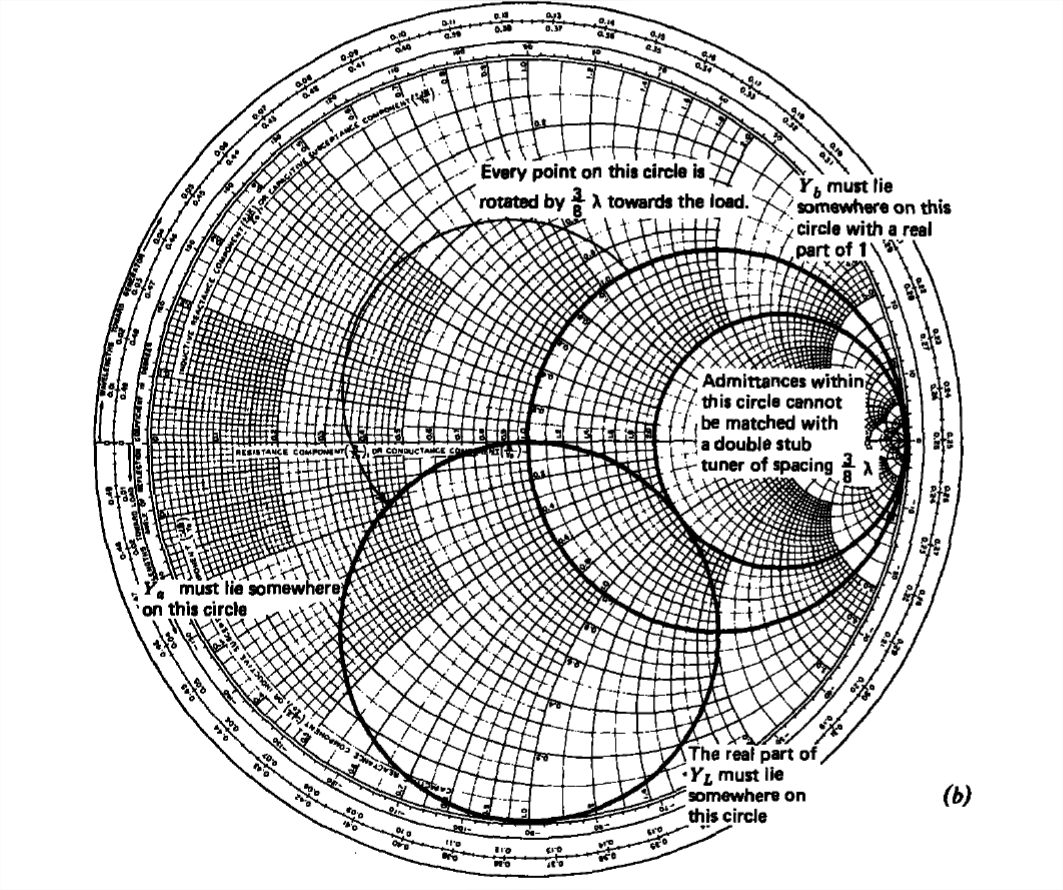
donde\(Y_{1}\) y\(Y_{2}\) son las admisiones puramente reactivas de los talones reflejadas de nuevo a las uniones mientras que\(Y_{b}\) es la admision de\(Y_{a}\) reflejada de vuelta hacia la carga por\(\frac{3}{8}\lambda \). Para un partido requerimos que\(Y_{n}\) sea unidad. Dado que\(Y_{2}\) es puramente imaginario, la parte real de\(Y_{b}\) debe estar en el círculo con una parte real de unidad. Entonces\(Y_{a}\) debe estar en algún lugar de este círculo cuando cada punto del círculo se refleja de nuevo por\(\frac{3}{8}\lambda \). Esto genera otro círculo que está de\(\frac{3}{2}\pi \) vuelta en sentido contrario a las agujas del reloj a medida que nos movemos hacia la carga, como se ilustra en la Figura 8-25b. Para encontrar las condiciones para un partido, trabajamos de izquierda a derecha hacia la carga usando el siguiente razonamiento:
- Dado que\(Y_{2}\) es puramente imaginario, la parte real de\(Y_{b}\) debe estar en el círculo con una parte real de unidad, como en la Figura 8-25b.
- Cada punto posible en\(Y_{b}\) debe reflejarse hacia la carga por\(\frac{3}{8}\lambda \) para encontrar el locus de posible coincidencia para\(Y_{a}\). Esto genera otro círculo que está de\(\frac{3}{2}\pi \) vuelta en sentido contrario a las agujas del reloj a medida que avanzamos hacia la carga, como en la Figura 8-25b.
Nuevamente dado que\(Y_{1}\) es puramente imaginario, la parte real de también\(Y_{a}\) debe ser igual a la parte real de la admisión de carga. Esto arroja dos posibles soluciones si la admisión de carga está fuera del círculo prohibido encerrando todas las admisiones de carga con una parte real mayor que\(2\). Solo las cargas con admitancias normalizadas cuya parte real es menor que\(2\) pueden ser igualadas por el afinador de doble trozo de\(\frac{3}{8}\lambda \) espaciado. Por supuesto, si una carga está dentro del círculo prohibido, puede ser igualada por un afinador de doble talón si el espaciado de los trozos es diferente a\(\frac{3}{8}\lambda \).
La impedancia de carga\(Z_{L}=50\left ( 1+j \right )\) en una\(50\)\(\textrm{Ohm}\) línea debe ser igualada por un sintonizador de\(\frac{3}{8}\lambda \) espaciado de doble tetón. ¿Qué longitudes de talón\( l_{1}\) y\( l_{2}\) son necesarias?
SOLUCIÓN
La impedancia de carga normalizada\(Z_{nL}=1+j\) corresponde a una admitancia de carga normalizada:
\(Y_{nL}=0.5\left ( 1-j \right )\)
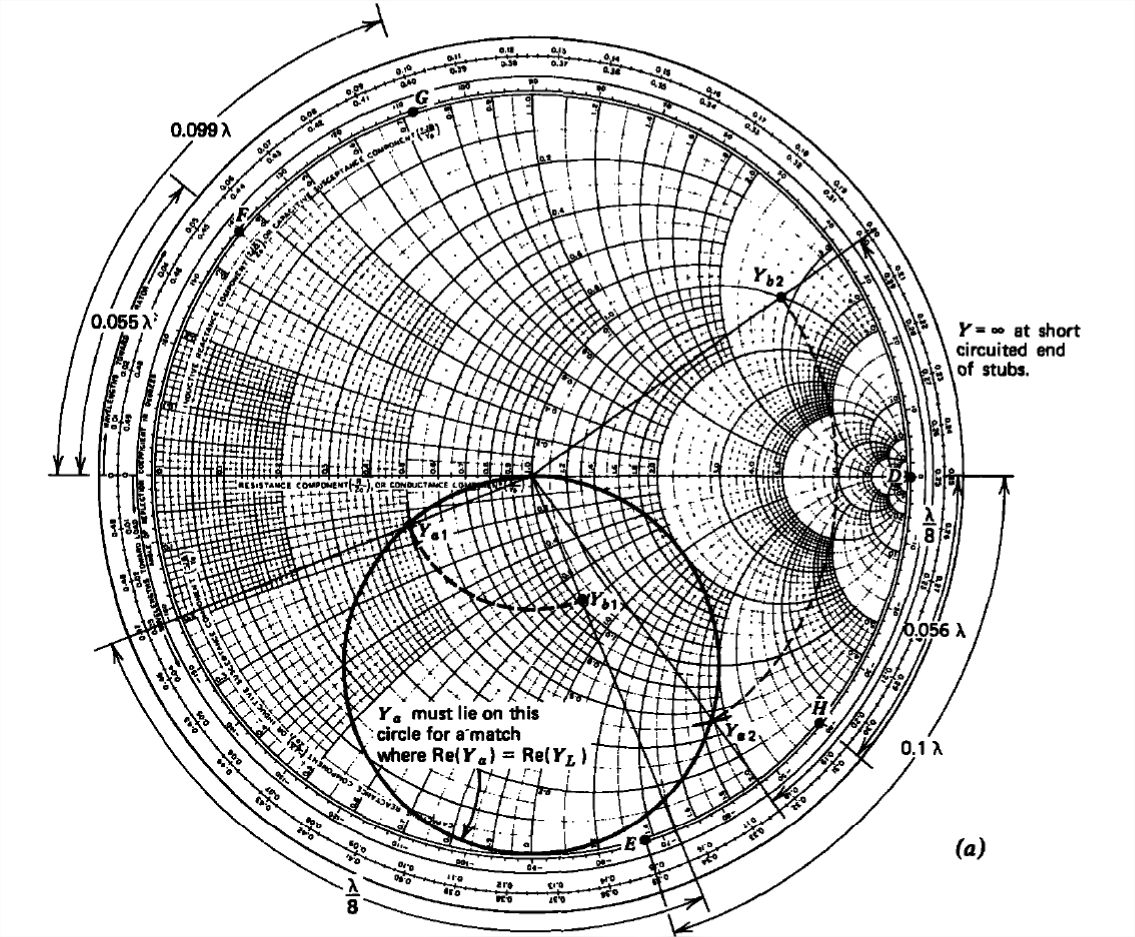
Luego las dos soluciones para se\(Y_{a}\) encuentran en la intersección del círculo que se muestra en la Figura 8-26a con el\(r = 0.5 \, \textrm{circle}\):
\ (Y_ {a1} =0.5-0.14j\\
Y_ {a2} =0.5-1.85j\)
Luego encontramos\(Y_{1}\) resolviendo para la parte imaginaria de la ecuación superior en (13):
\ (Y_ {1} =j\ textrm {Im}\ izquierda (Y_ {a} -Y_ {L}\ derecha) =\ izquierda\ {\ comenzar {matriz}
0.36j\ Rightarrow l_ {1} =0.305\ lambda\,\ izquierda (F\ derecha)\\
-1.35j\ Rightarrow l_ {1} =0.1\ lambda\,\ izquierda (E\ derecha)
\ end {matriz}\ derecha.\)
Al girar las\(Y_{a}\) soluciones de\(\frac{3}{8}\lambda \) nuevo al generador (en\(270^{\circ }\) sentido horario, lo que equivale a\(90^{\circ }\) antihorario), su intersección con el\(r = 1\) círculo da las soluciones para\(Y_{b}\) como
\ (Y_ {b1} =1.0-0.72j\\
Y_ {b2} =1.0+2.7j\)
Esto requiere\(Y_{2}\) ser
\ (Y_ {2} =-j\ textrm {Im}\ izquierda (Y_ {b}\ derecha) =\ izquierda\ {\ comenzar {matriz}
0.72j\ Rightarrow l_ {2} =0.349\ lambda\,\ izquierda (G\ derecha)\
-2.7j\ Rightarrow l_ {2} =0.056\ lambda\,\ izquierda (H\ derecha)
\ final {matriz}\ derecha.\)
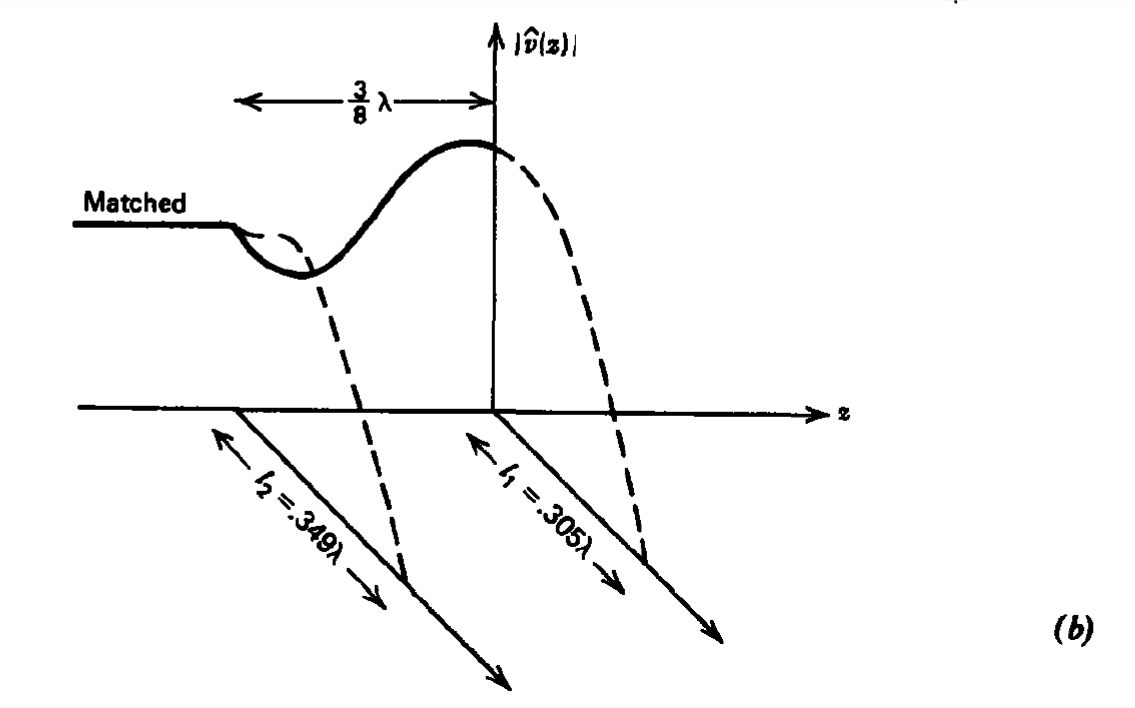
El patrón de onda estacionaria de voltaje a lo largo de la línea y los stubs se muestra en la Figura 8.26b. Observe la continuidad del voltaje en las uniones. Las longitudes reales del stub pueden ser las enumeradas más cualquier múltiplo entero de\(\lambda /2\).


