8.8: Problemas
- Page ID
- 86937
Sección 8-1
Encuentre la inductancia y capacitancia por unidad de longitud y la impedancia característica para el cable sobre el plano y la línea de dos hilos que se muestran en la Figura 8-3. (Pista: Ver Sección 2-6-4c.)
La inductancia y capacitancia por unidad de longitud en una línea de transmisión sin pérdidas es una función débil de\(z\) ya que la distancia entre electrodos cambia lentamente con\(z\).
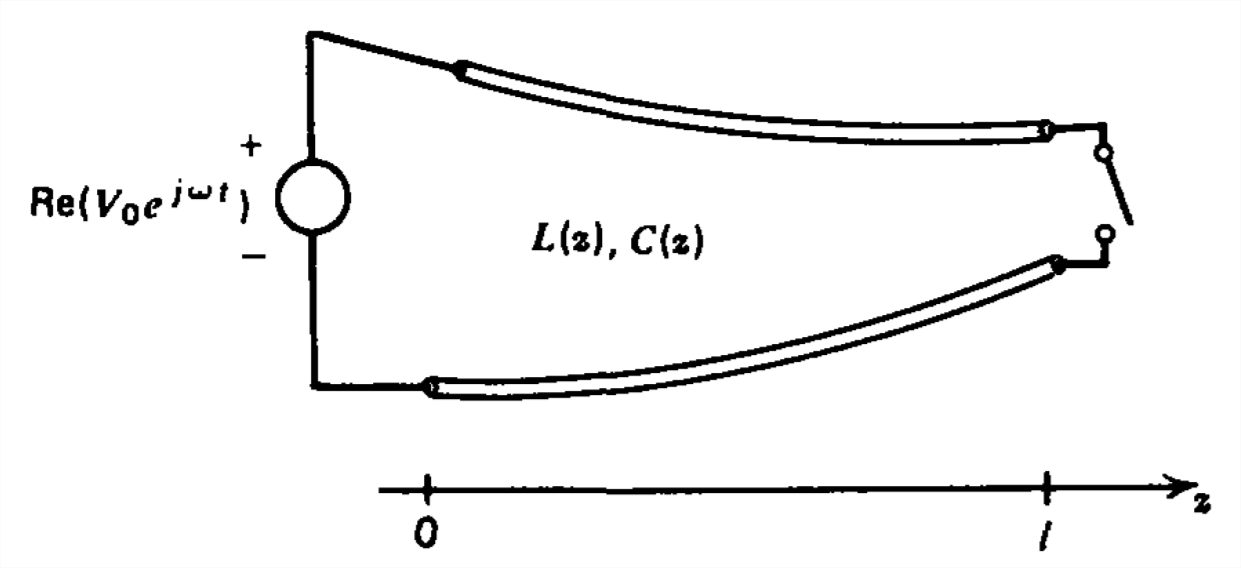
(a) Para este caso escribir las ecuaciones de la línea de transmisión como ecuaciones simples en voltaje y corriente.
b) Considerar una línea exponencial, donde
\(L\left ( z \right )=L_{0}e^{\alpha z},\quad C\left ( z \right )=C_{0}e^{-\alpha z}\)
Si el voltaje y la corriente varían sinusoidalmente con el tiempo como
\(v\left ( z,t \right )=\textrm{Re}\left [ \hat{v}\left ( z \right )e^{j\omega t} \right ],\quad i\left ( z,t \right )=\textrm{Re}\left [ \hat{\pmb{\imath}}\left ( z \right )e^{j\omega t} \right ]\)
encontrar la forma general de solución para las distribuciones espaciales de\(\hat{v}\left ( z \right )\) y\(\hat{\pmb{\imath}}\left ( z \right )\).
(c) La línea de transmisión es excitada por una fuente de voltaje\(V_{0}\cos \omega t\) en\(z=0\). ¿Cuáles son las distribuciones de voltaje y corriente si la línea está en cortocircuito o en circuito abierto\(z=l\)?
d) ¿Para qué rango de frecuencia las ondas se decaen estrictamente con la distancia? ¿Cuál es la frecuencia de corte para la propagación de ondas?
e) ¿Cuáles son las frecuencias resonantes de la línea cortocircuitada?
(f) Qué condición determina las frecuencias resonantes de la línea de circuito abierto.
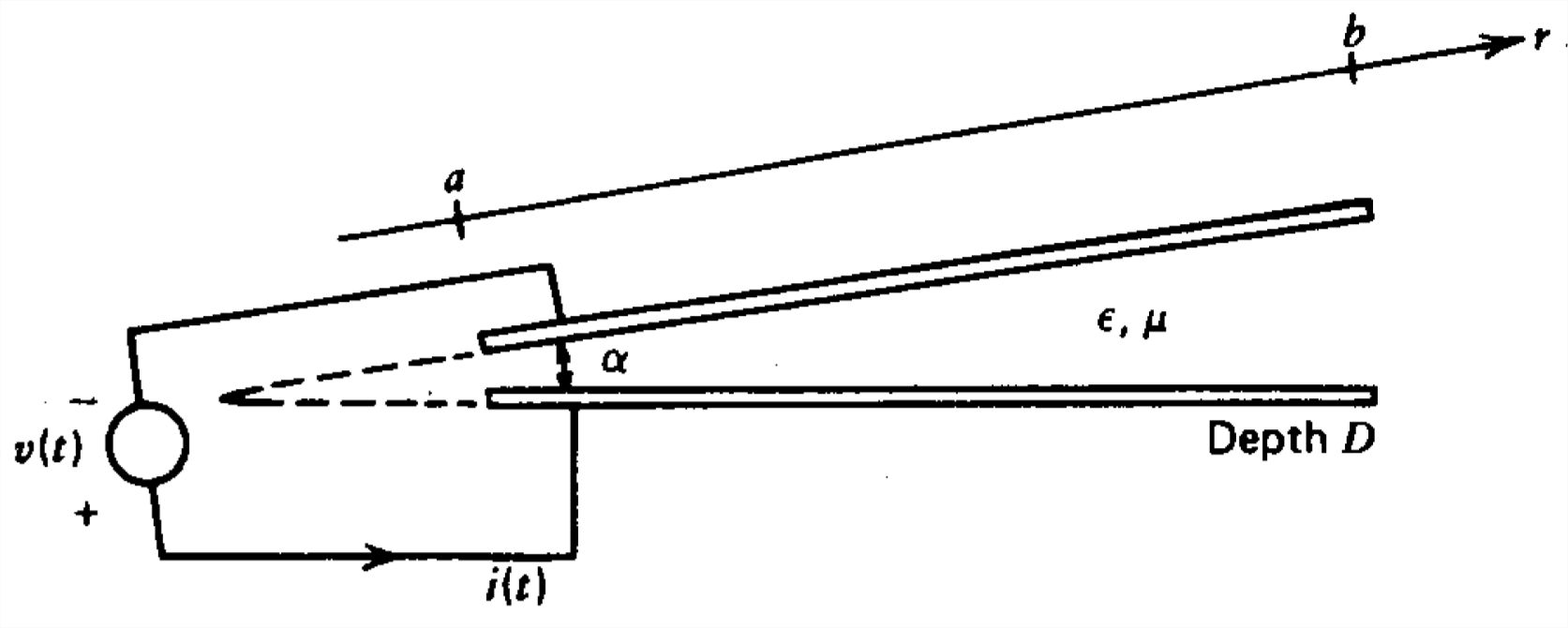
Dos conductores de longitud\(l\) que se extienden sobre la distancia radial\(a\leq \textrm{r}\leq b\) están\(\alpha \) separados por un ángulo constante.
a) ¿Cuáles son los campos eléctricos y magnéticos en términos de voltaje y corriente?
(b) Encontrar la inductancia y capacitancia por unidad de longitud. ¿Cuál es la impedancia característica?
Una línea de transmisión de placa paralela se llena con un plasma conductor con ley constitutiva
\(\frac{\partial \textbf{J}}{\partial t}=\omega_{p}^{2}\varepsilon \textbf{E}\)
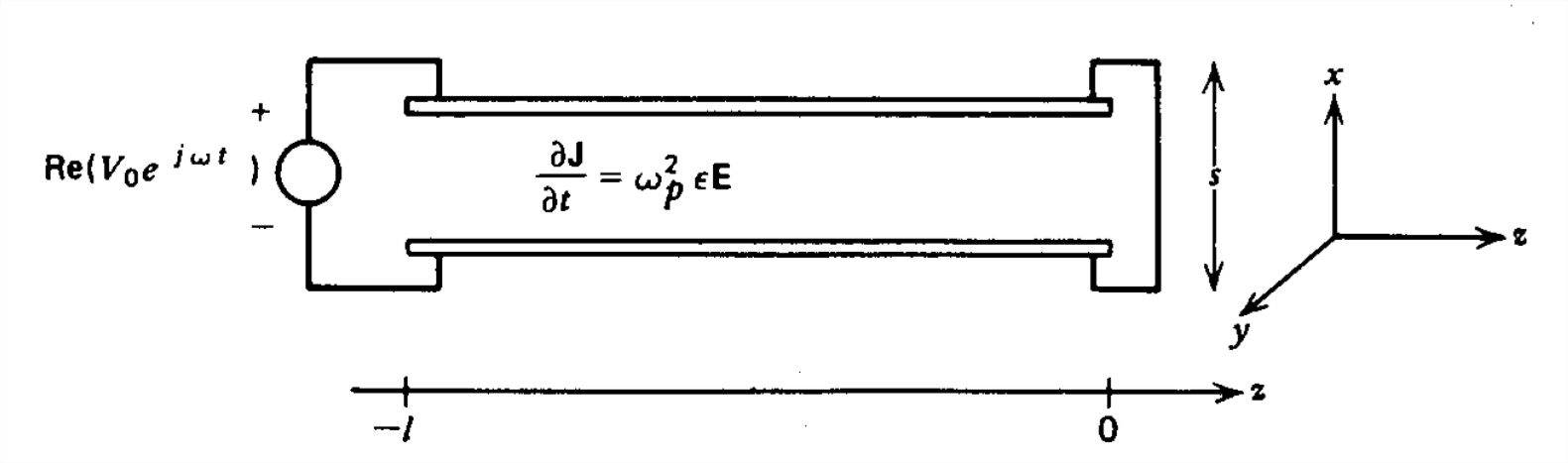
a) ¿Cómo se relacionan los campos eléctrico y magnético?
b) ¿Cuáles son las ecuaciones de la línea de transmisión para el voltaje y la corriente?
c) Para las señales sinusoidales de la forma\(e^{j\left ( \omega t-kz \right )}\), ¿cómo están\(\omega\) y\(k\) relacionadas? ¿Sobre qué rango de frecuencia tenemos propagación o decaimiento?
(d) La línea de transmisión está cortocircuitada\(z = 0\) y excitada por una fuente de voltaje\(V_{0}\cos \omega t\) en\(z=-l\). ¿Cuáles son las distribuciones de voltaje y corriente?
e) ¿Cuáles son las frecuencias resonantes del sistema?
Un tipo inusual de sistema distribuido está formado por condensadores en serie e inductores de derivación.
a) ¿Cuáles son las ecuaciones diferenciales parciales gobernantes que relacionan la tensión y la corriente?
b) ¿Cuál es la relación de dispersión entre\(\omega \) y\(k\) para señales de la forma\(e^{j\left ( \omega t-kz \right )}\)?
c) ¿Cuáles son las velocidades de grupo y fase de las olas? ¿Por qué tales sistemas se llaman “onda hacia atrás”?
(d)\(V_{0}\cos \omega t\) Se aplica un voltaje\(z=-l\) con el\(z= 0\) extremo cortocircuitado. ¿Cuáles son las distribuciones de voltaje y corriente a lo largo de la línea?
e) ¿Cuáles son las frecuencias resonantes del sistema?
Sección 8-2
Una línea de transmisión infinitamente larga se excita en su centro por un voltaje\(V_{0}\) escalonado encendido en\(t=0\). La línea está inicialmente en reposo.
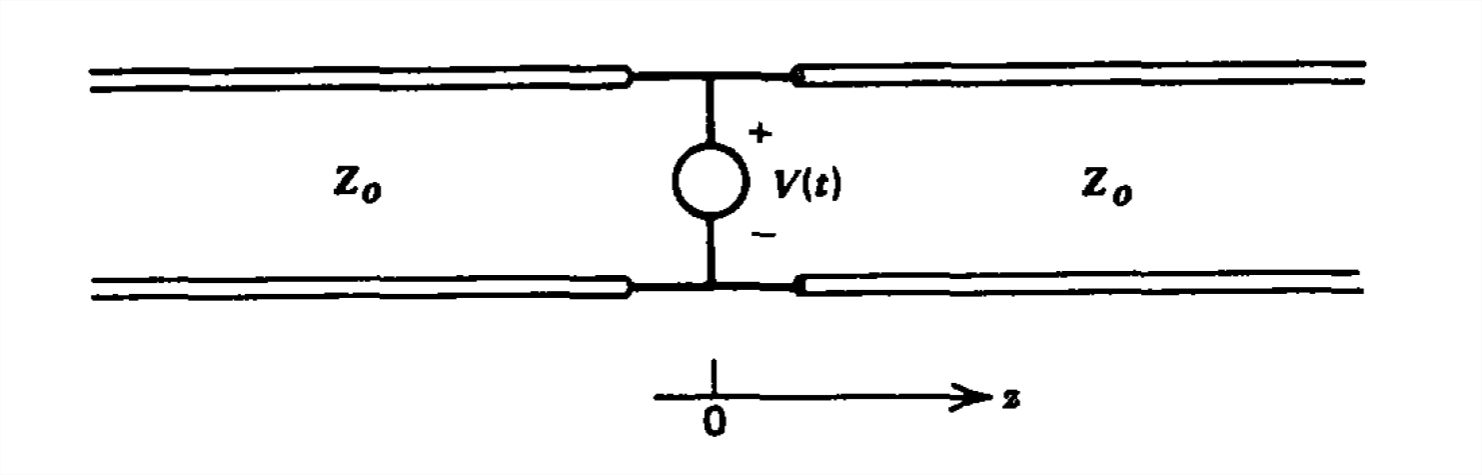
(a) Trazar las distribuciones de voltaje y corriente en el momento\(T\).
(b) En este momento\(T\) el voltaje se establece en cero. Trazar el voltaje y la corriente en todas partes a la vez\(2T\).
Una línea de transmisión de longitud\(l\) excitada por una fuente de voltaje escalonado tiene sus extremos conectados entre sí. Trazar el voltaje y la corriente en\(z=l/4\),\(l/2\) y\(3l/4\) en función del tiempo.
El estado estacionario de CC se alcanza para una línea de transmisión cargada\(z=l\) con una resistencia\(R_L\) y excitada\(z=0\) por un voltaje de CC\(V_{0}\) aplicado a través de una resistencia de fuente\(R_s\). La fuente de voltaje se establece repentinamente en cero en\(t=0\).
(a) ¿Cuál es el voltaje inicial y la corriente a lo largo de la línea?
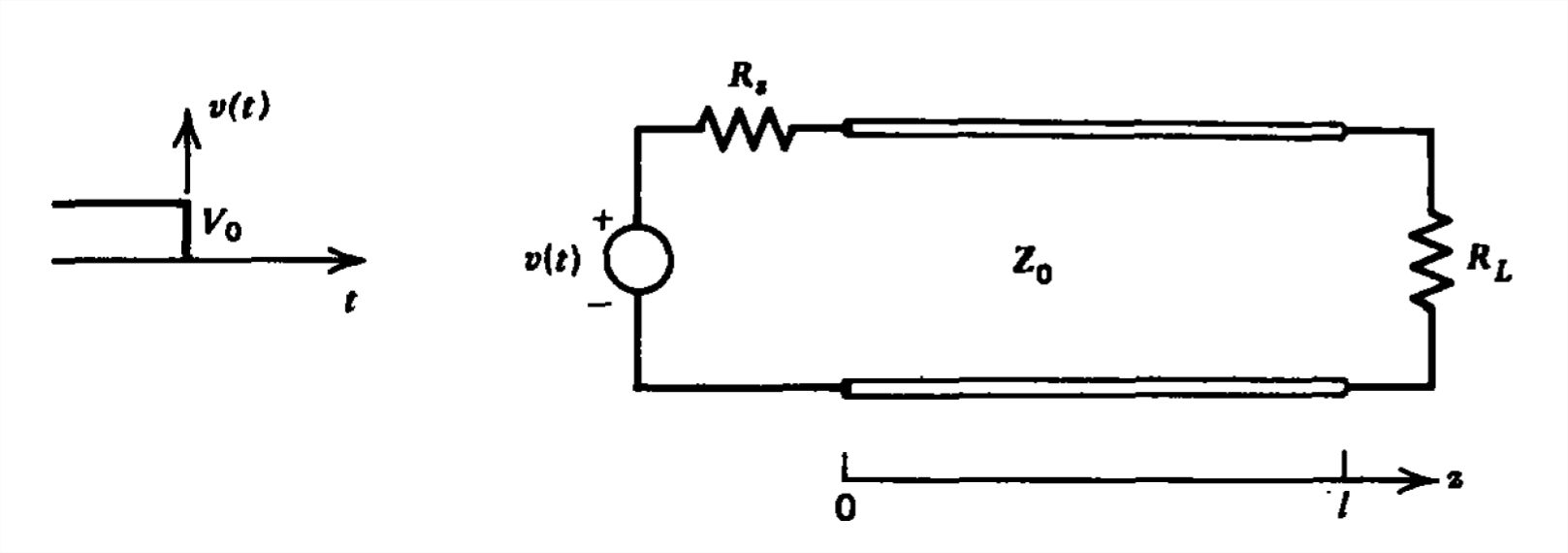
(b) Encontrar el voltaje al\(z=l\) final en función del tiempo. (Pista: Usa ecuaciones de diferencia.)
Una fuente de corriente escalonada encendida en\(t = 0\) se conecta al\(z=0\) final de una línea de transmisión en paralelo con una resistencia de fuente\(R_s\). Una resistencia de carga\(R_L\) está conectada en\(z=l\).
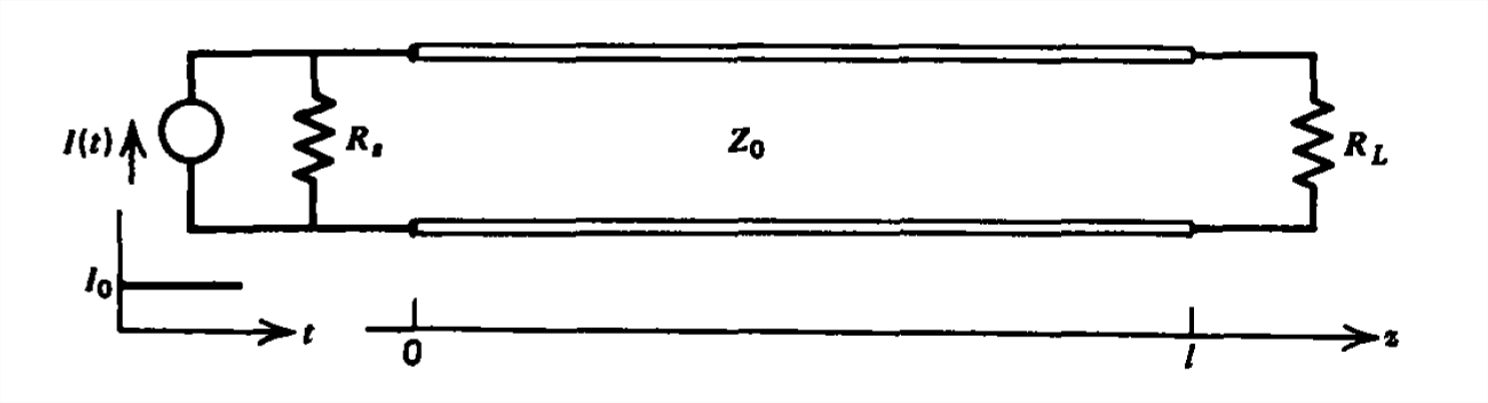
(a) ¿Cuál es el voltaje y la corriente de carga en función del tiempo? (Pista: Utilice una red equivalente a Thevenin en\(z =0\) con los resultados de la Sección 8-2-3.)
(b) Con\(R_s=\infty \) parcela versus tiempo el voltaje de carga cuando\(R_L=\infty \) y la corriente de carga cuando\(R_L=0\).
(c) Si\(R_s=\infty \) y\(R_L=\infty \), resolver para el voltaje de carga en el límite cuasiestático asumiendo que la línea de transmisión es un condensador. Comparar con (b).
d) Si\(R_s\) es finito pero\(R_L=0\), ¿cuál es la dependencia temporal de la corriente de carga?
e) Repetir (d) en el límite cuasiestático donde la línea de transmisión se comporta como inductor. ¿Cuándo son los resultados de (d) y (e) aproximadamente iguales?
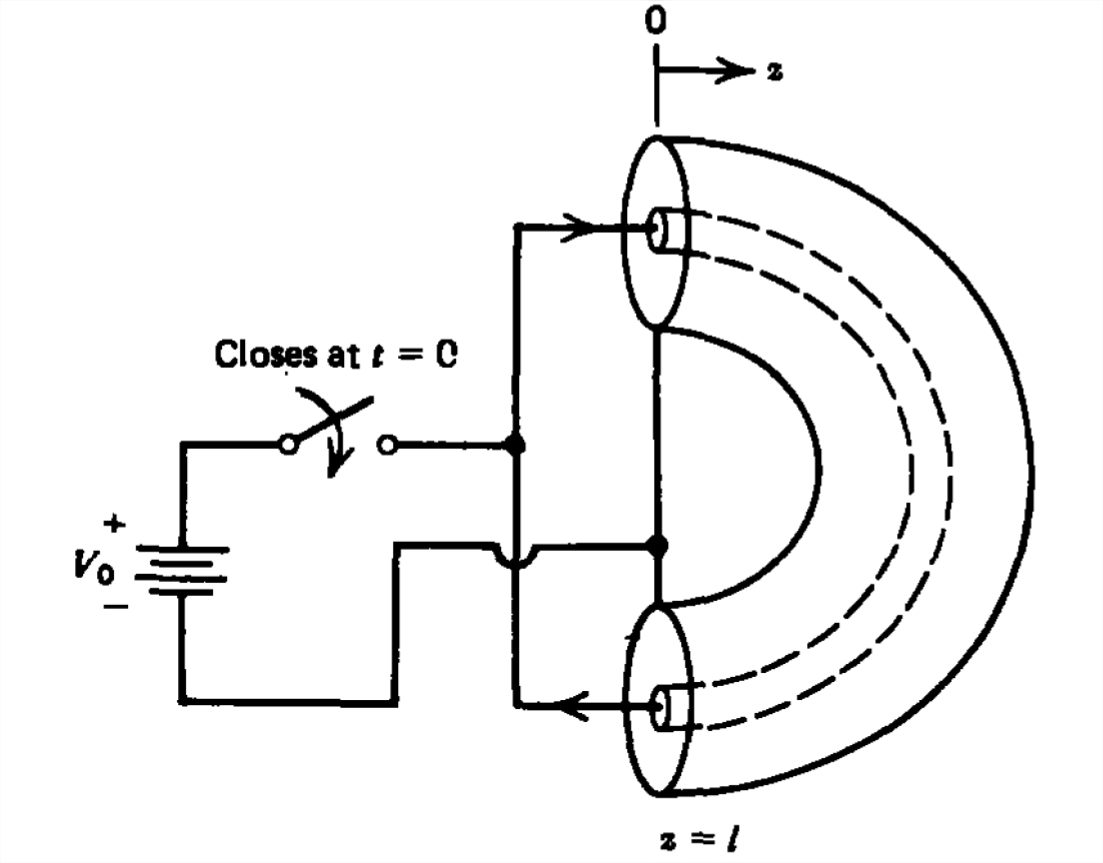
Los sistemas de línea de transmisión conmutada con un voltaje de CC inicial se pueden utilizar para generar pulsos de alto voltaje de corta duración. La línea que se muestra se carga hasta un voltaje de CC\(V_{0}\) cuando en\(t =0\) el interruptor de carga está cerrado y el interruptor de fuente está abierto.
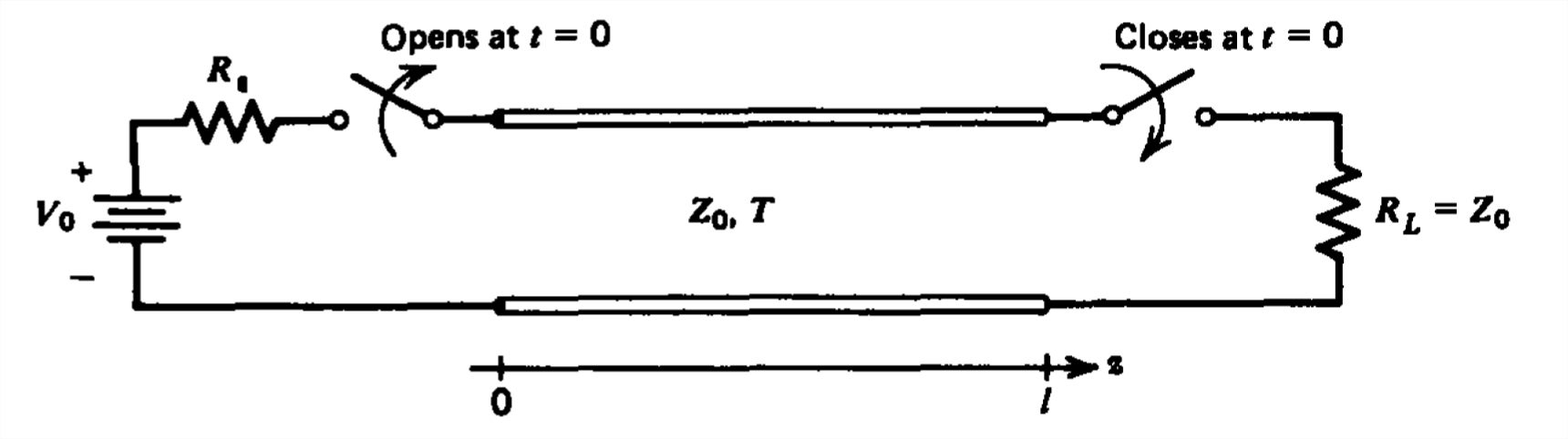
(a) ¿Cuál es el voltaje y la corriente de línea inicial? ¿Qué son\(V_{+}\) y\(V_{-}\)?
(b) Esbozar la dependencia del tiempo de la tensión de carga.
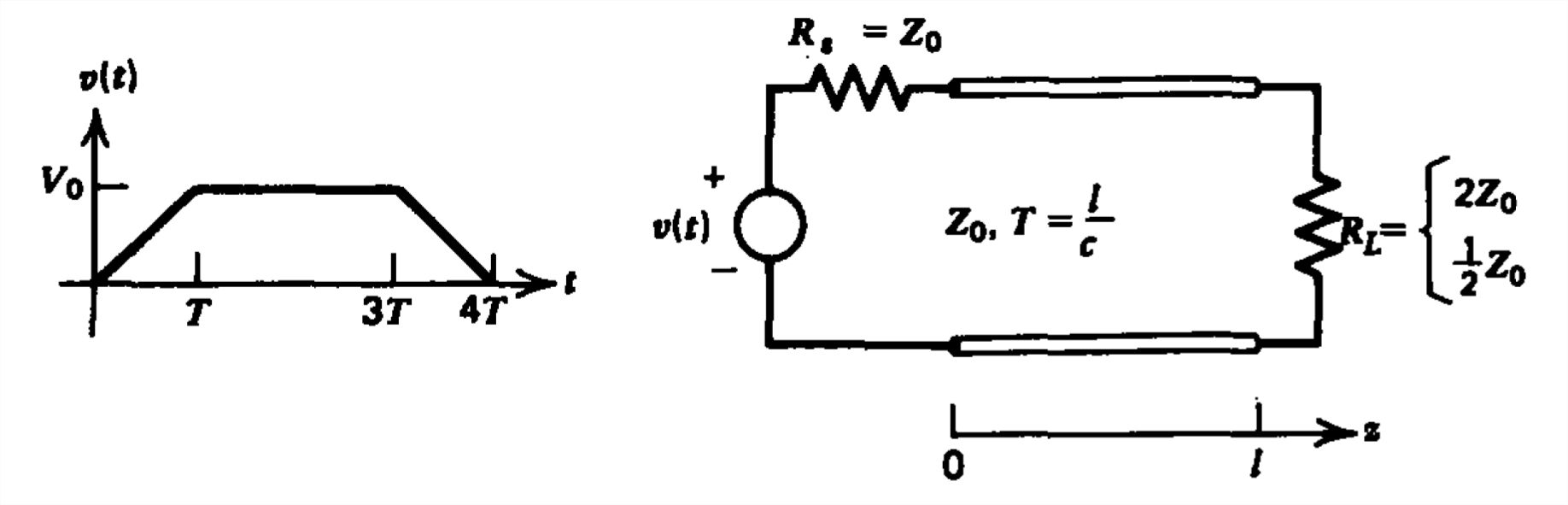
Para la excitación de voltaje trapezoidal mostrada, grafica versus tiempo las formas de onda actuales en\(z =0\) y\(z=l\) para\(R_{L}=2Z_{0}\) y\(R_{L}=\frac{1}{2}Z_{0}\).
Se aplica un voltaje de paso a una línea de transmisión cargada con\(R_{L}=2Z_{0}\) una resistencia de fuente coincidente.
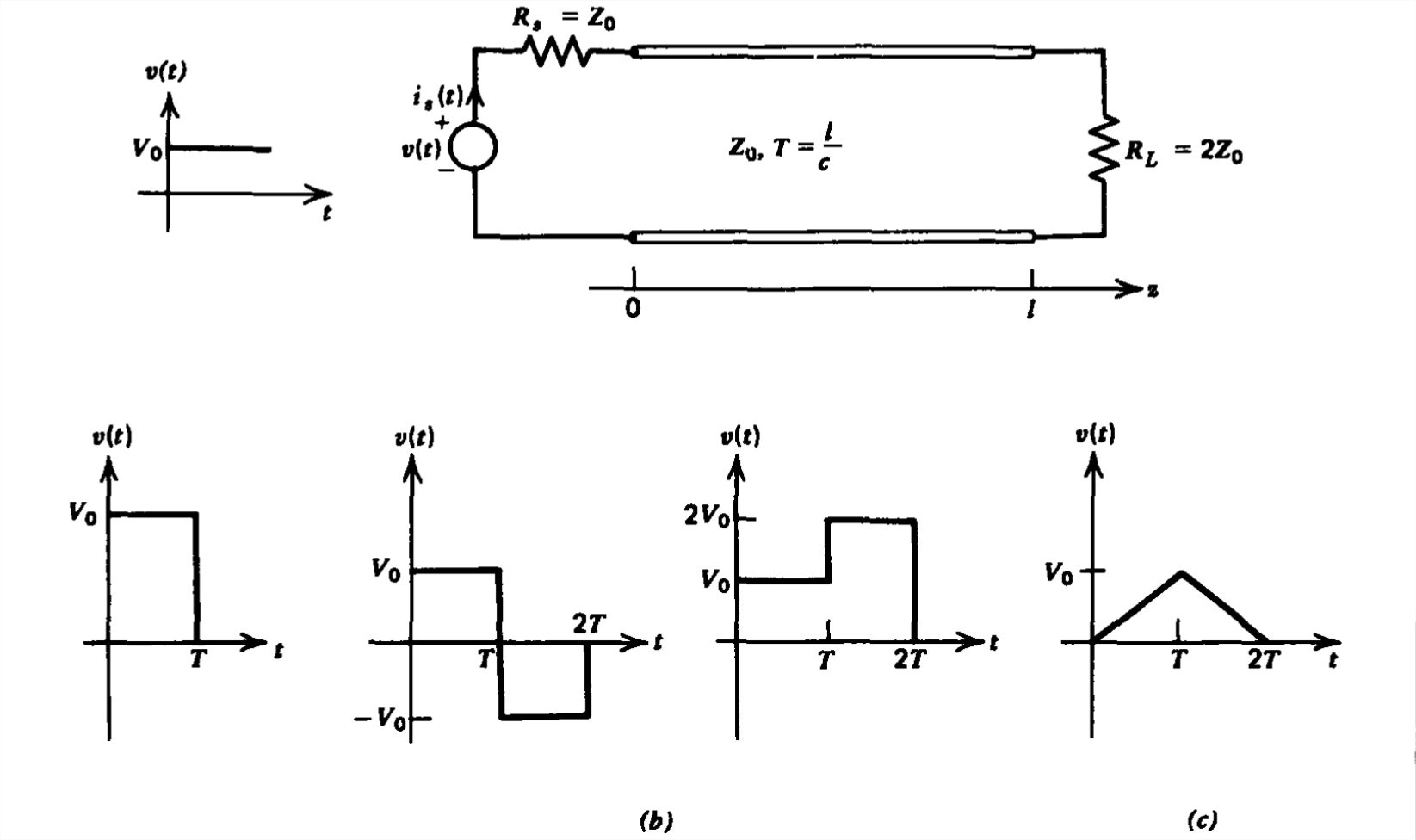
(a) Esbozar la corriente de origen\(i_{s}\left ( t \right )\).
(b) Utilizando superposición de voltajes de paso retardados, se encuentra la dependencia del tiempo\(i_{s}\left ( t \right )\) para los diversos voltajes de pulso mostrados.
(c) Al integrar la solución apropiada de (b), encontrar\(i_{s}\left ( t \right )\) si el voltaje aplicado es la onda triangular mostrada.
Se ha aplicado un voltaje de CC durante mucho tiempo al circuito de línea de transmisión que se muestra con interruptores\(S_{1}\) y se\(S_{2}\) abre cuando está en\(t=0\):
(a)\(S_{2}\) se cierra repentinamente con\(S_{1}\) mantenido abierto;
b)\(S_{1}\) se cierra súbitamente con\(S_{2}\) mantenido abierto;
c) Ambos\(S_{1}\) y\(S_{2}\) están cerrados.
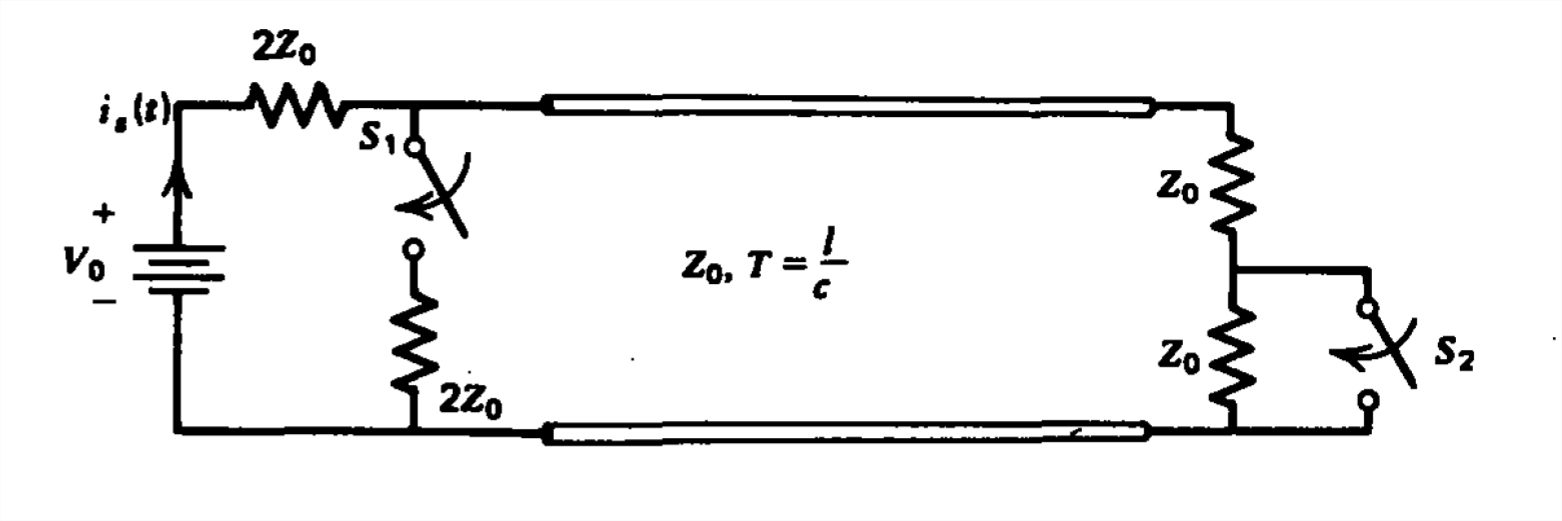
Para cada uno de estos casos se traza la corriente de origen\(i_{s}\left ( t \right )\) versus el tiempo.
Para cada uno de los circuitos de línea de transmisión mostrados, el interruptor se abre\(t=0\) después de que se haya aplicado el voltaje de CC durante mucho tiempo.
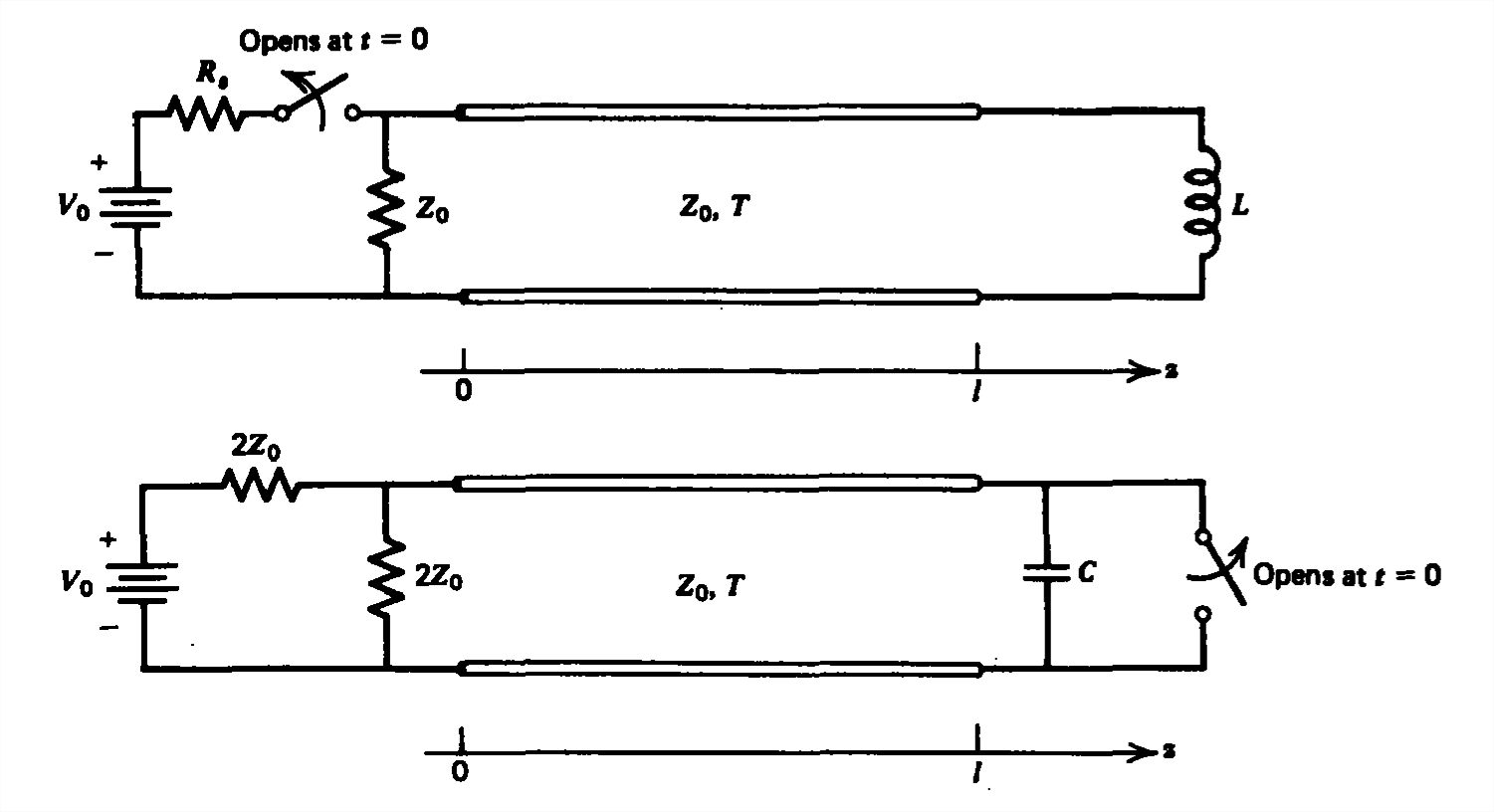
(a) ¿Cuáles son los voltajes y corrientes de la línea de transmisión justo antes de que se abran los interruptores? ¿Qué son\(V_{+}\) y\(V_{-}\) en\(t=0\)?
(b) Trazar el voltaje y la corriente en función del tiempo en
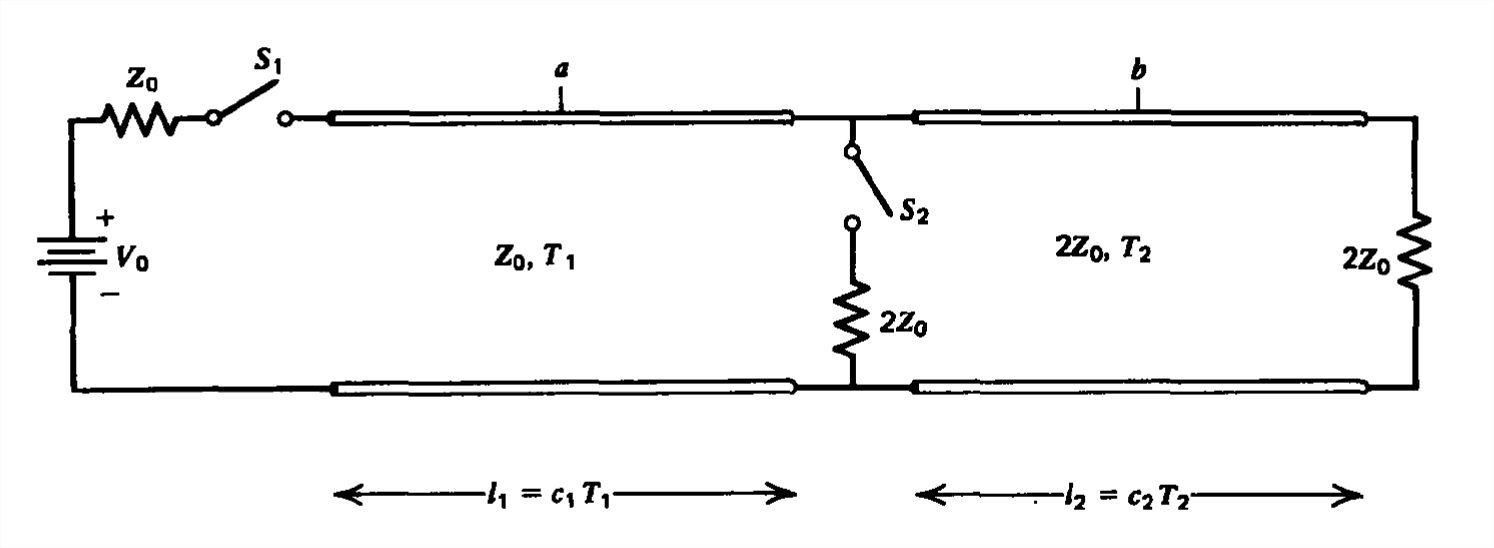
Una línea de transmisión está conectada a otra línea de transmisión con el doble de impedancia característica.
(a) Con el interruptor\(S_{2}\) abierto, el interruptor\(S_{1}\) se cierra repentinamente en\(t=0\). Trazar el voltaje y la corriente en función del tiempo a mitad de camino hacia abajo de cada línea en puntos\(a\) y\(b\).
b) Repetir (a) si\(S_{2}\) está cerrado.
Sección 8-3
Una línea de transmisión es excitada por una fuente de voltaje\(V_{0}\cos \omega t\) en\(z=-l\). La línea de transmisión se carga con una carga puramente reactiva con impedancia\(jX\) en\(z =0\).
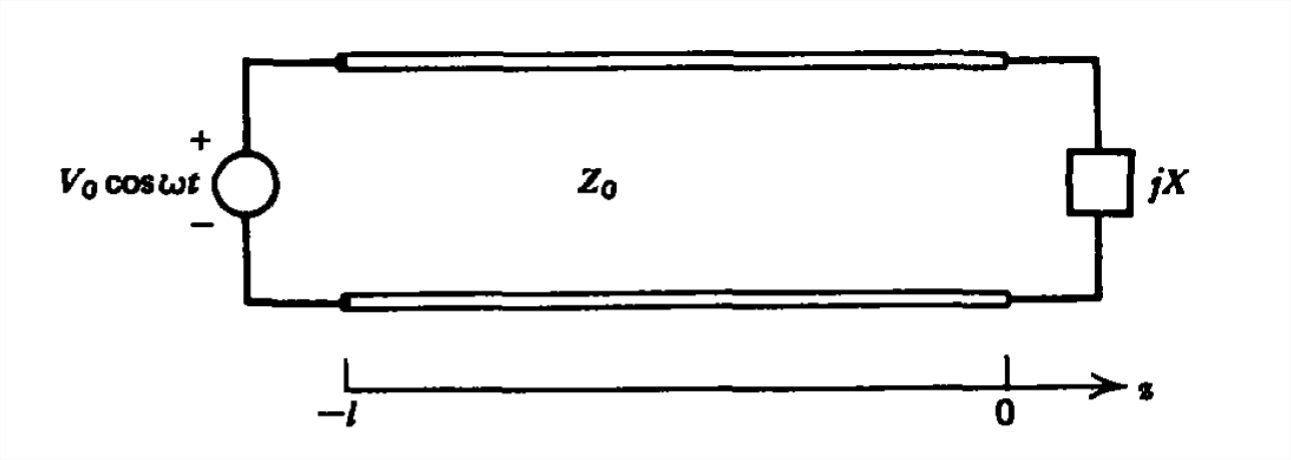
(a) Encuentre la distribución de voltaje y corriente a lo largo de la línea.
(b) Encontrar una expresión para las frecuencias resonantes del sistema si la carga es capacitiva o inductiva. ¿Cuál es la solución si\(\left | X \right |=Z_{0}\)?
(c) Repita (a) y (b) si la línea de transmisión es excitada por una fuente de corriente\(I_{0}\cos \omega t\) en\(z=-l\).
(a) Encontrar la resistencia y conductancia por unidad de longitudes para un cable coaxial cuyo dieléctrico tiene una conductividad óhmica pequeña\(\sigma \) y las paredes tienen una conductividad grande\(\sigma _{w}\), (Pista: La profundidad de la piel\(\delta \) es mucho menor que los radios o el grosor de cualquiera de los conductores.)
b) ¿Cuál es la tasa de decaimiento de los campos por las pérdidas?
(c) Si el dieléctrico no tiene pérdidas\(\left ( \sigma =0 \right )\) con un valor fijo del radio exterior\(b\), ¿qué valor del radio interior\(a\) minimizará la tasa de decaimiento? (Pista:\(1+1/3.6\approx \textrm{ln}\,3.6\).)
Una línea de transmisión de longitud\(l\) es cargada por una resistencia\(R_{L}\).
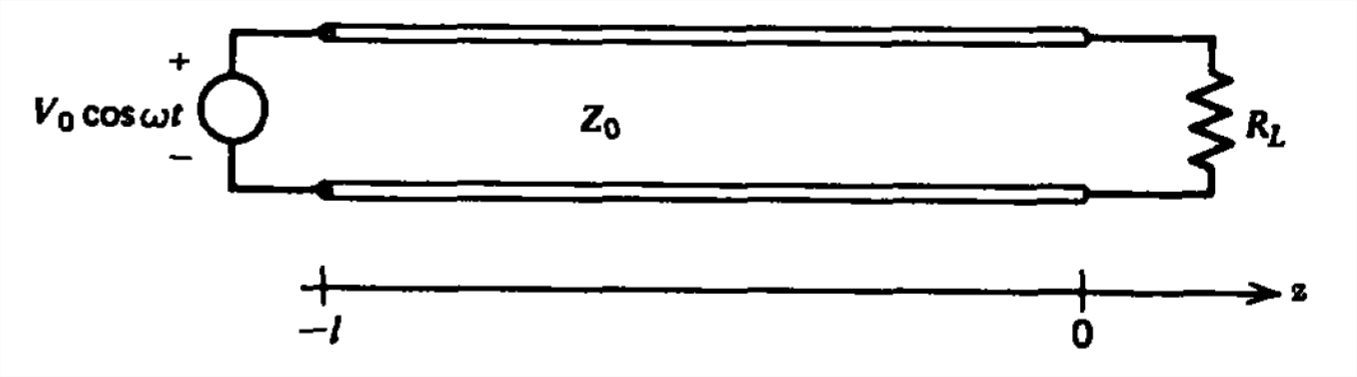
(a) Encuentre las distribuciones de voltaje y corriente a lo largo de la línea.
b) Reducir las soluciones de (a) cuando la línea es mucho más corta que una longitud de onda.
(c) Encontrar los circuitos equivalentes aproximados en el límite de longitud de onda larga\(\left ( kl\ll 1 \right )\) cuando\(R_{L}\) es muy pequeño\(\left ( R_{L}\ll Z_{0} \right )\) y cuando es muy grande\(\left ( R_{L}\gg Z_{0} \right )\).
Sección 8-4
Para la línea de transmisión que se muestra:
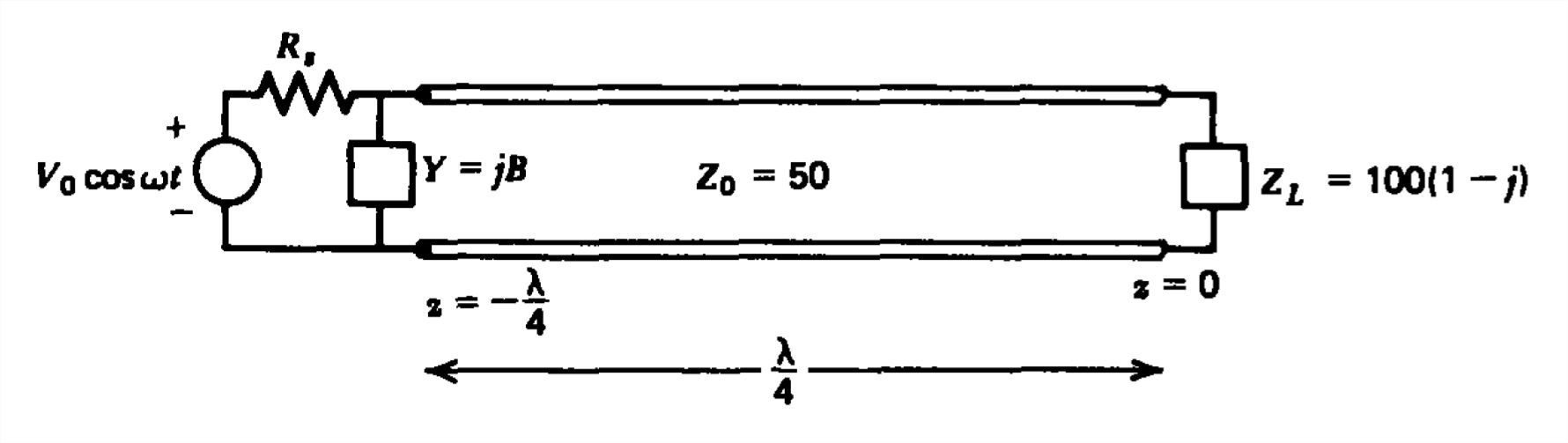
(a) Encontrar los valores de admitancia reactiva agrupada\(Y=jB\) y resistencia de fuente distinta de cero\(R_{s}\) que maximice la potencia entregada por la fuente. (Pista: No utilice el gráfico Smith.)
b) ¿Cuál es la potencia promedio de tiempo disipada en la carga?
(a) Encuentre la potencia promedio de tiempo entregada por la fuente para el sistema de línea de transmisión que se muestra cuando el interruptor está abierto o cerrado. (Pista: No utilice el gráfico Smith.)
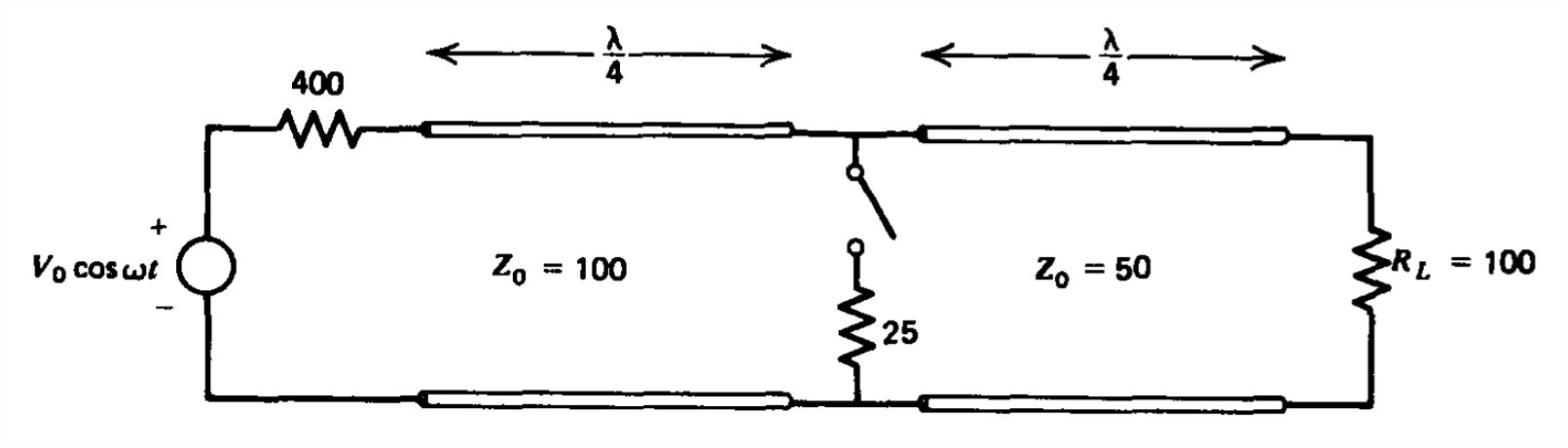
(b) Para cada posición del interruptor, ¿cuál es la potencia promedio de tiempo disipada en la resistencia de carga\(R_{L}\)?
(c) Para cada posición de interruptor ¿cuál es el\(\textrm{VSWR}\) en cada línea?
(a) Usando el gráfico Smith, encuentre la corriente de origen entregada (magnitud y fase) para el sistema de línea de transmisión que se muestra\(l=\lambda /8\), para\(\lambda /4\),\(3\lambda /8\), y\(\lambda /2\).
b) Para cada valor de\(l\), ¿cuáles son las potencias promedio en el tiempo entregadas por la fuente y disipadas en la impedancia de carga\(Z_{L}\)?
c) ¿Cuál es el\(\textrm{VSWR}\)?
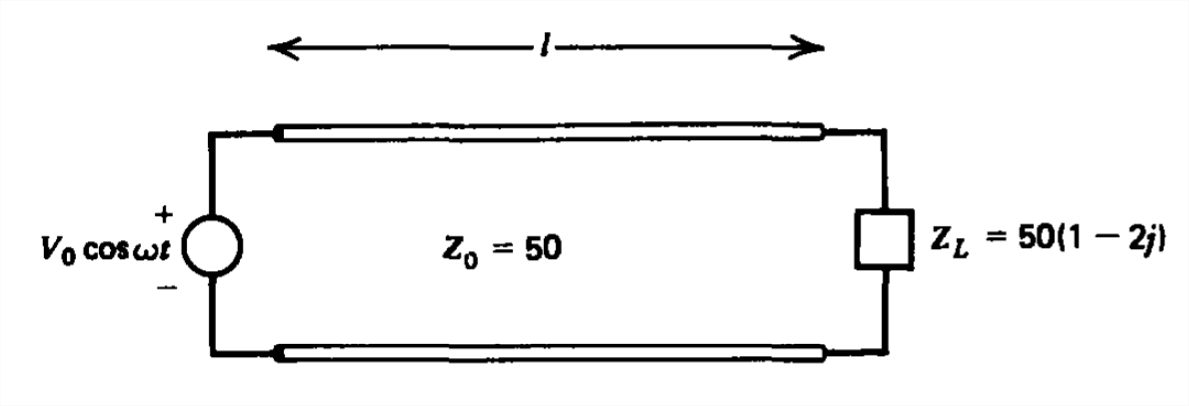
(a) Sin usar la gráfica Smith, encuentre las distribuciones de voltaje y corriente para el sistema de línea de transmisión que se muestra.
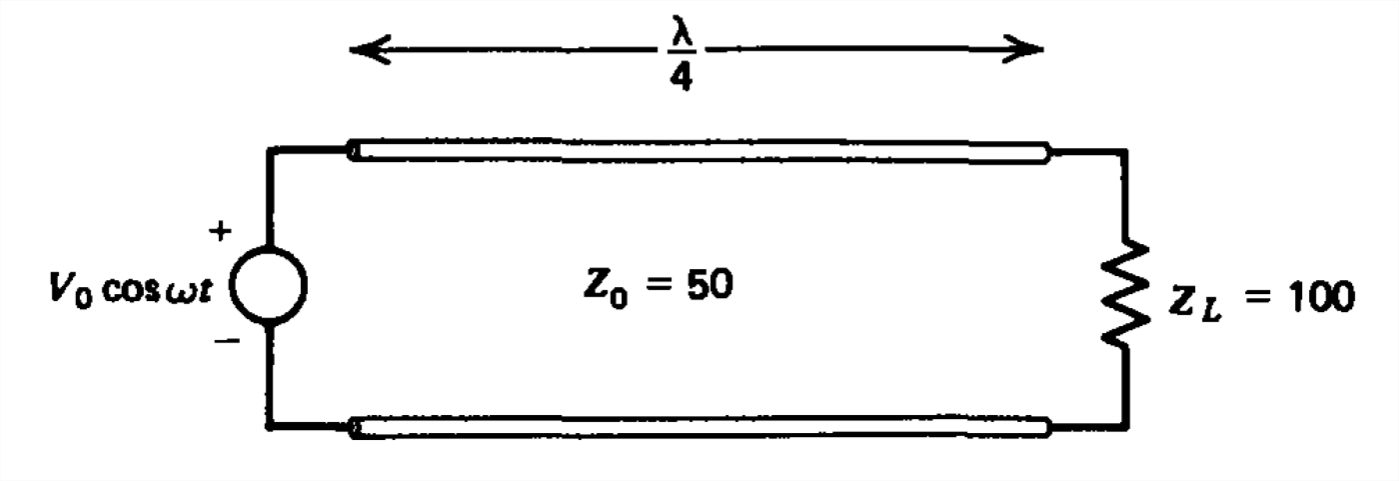
b) ¿Cuál es el\(\textrm{VSWR}\)?
c) ¿En qué posiciones los voltajes son máximos o mínimos? ¿Cuál es la magnitud del voltaje en estas posiciones?
El\(\textrm{VSWR}\) en una línea\(100 \textrm{Ohm}\) de transmisión es\(3\). La distancia entre mínimos de voltaje sucesivos es\(50\,\textrm{cm}\) mientras que la distancia desde la carga hasta los primeros mínimos es\(20\,\textrm{cm}\). ¿Cuáles son el coeficiente de reflexión y la impedancia de carga?
Sección 8-5
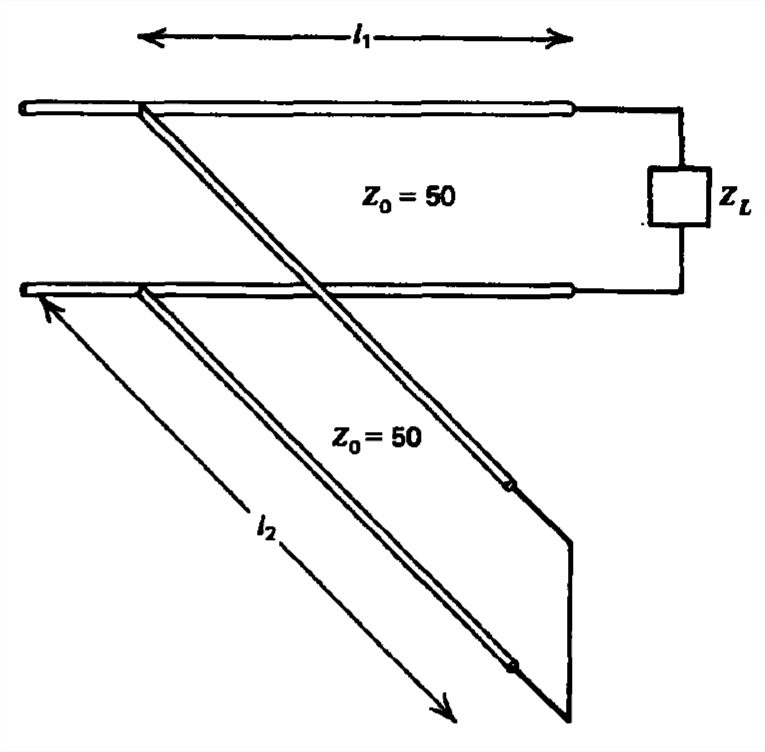
Para cada una de las siguientes impedancias de carga en el sistema de línea de transmisión de sintonización de un solo trozo que se muestra, encuentre todos los valores de la longitud de la línea\(l_1\) y la longitud del trozo\(l_2\) necesarios para hacer coincidir la carga con la línea.
a\(Z_L=100\left ( 1-j \right )\)) c\(Z_L=25\left ( 2-j \right )\)
b\(Z_L=50\left ( 1+2j \right )\)) d\(Z_L=25\left ( 1+2j \right )\)
Para cada una de las siguientes impedancias de carga en el sistema de línea de transmisión de sintonización de doble talón que se muestra, encuentre longitudes de muñón\(l_1\) y\(l_2\) haga coincidir la carga con la línea.
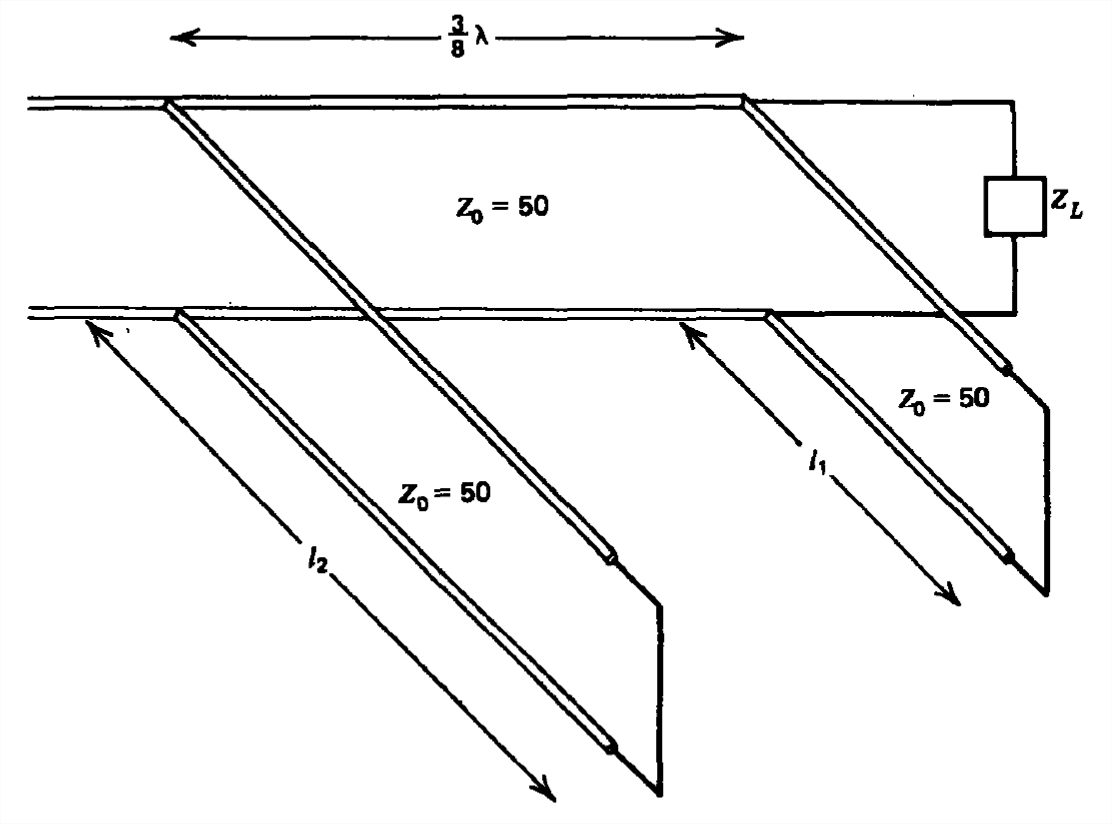
a\(Z_L=100\left ( 1-j \right )\)) c\(Z_L=25\left ( 2-j \right )\)
b\(Z_L=50\left ( 1+2j \right )\)) d\(Z_L=25\left ( 1+2j \right )\)
(a) Sin usar el gráfico Smith, encuentre la impedancia de entrada\(Z_{in}\) en\(z=-l=-\lambda /4\) para cada una de las cargas mostradas.
b) ¿Cuál es la corriente de entrada\(i\left ( z=-l,t \right )\) para cada una de las cargas?
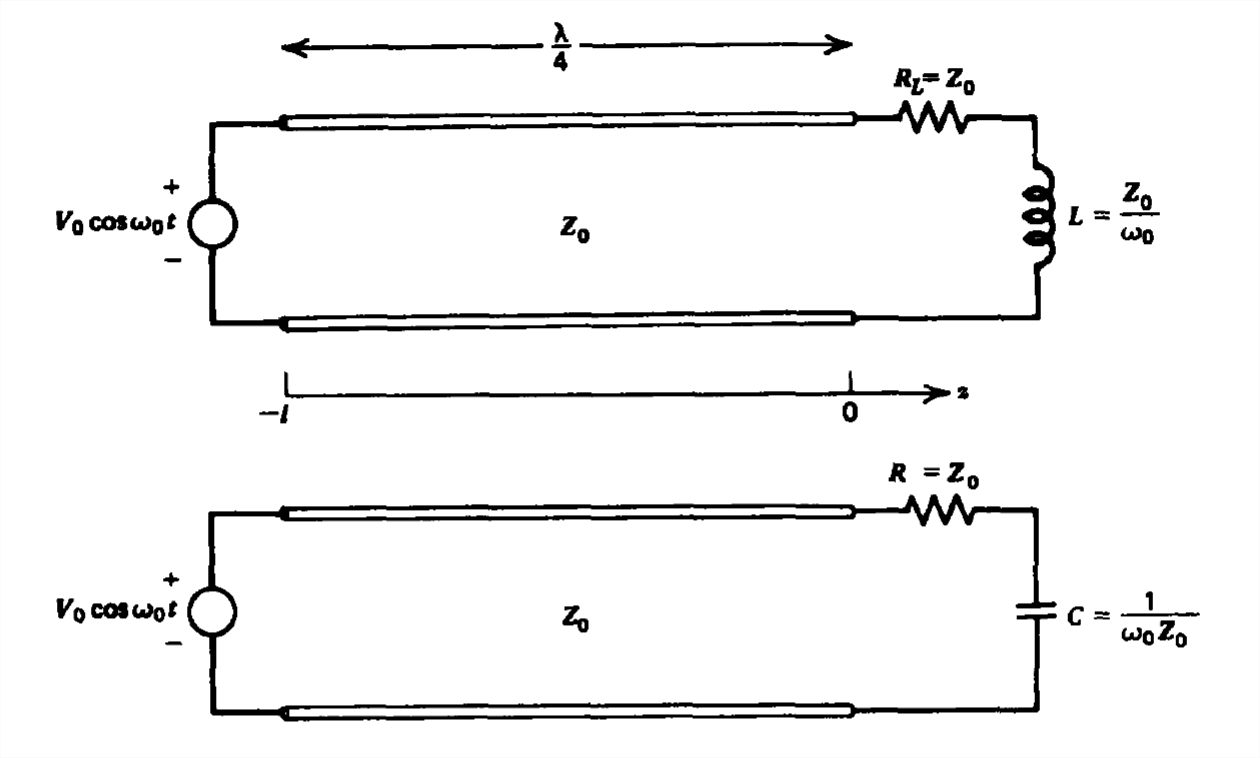
c) La frecuencia de la fuente se duplica a\(2\omega _{0}\). La longitud de la línea\(l\) y las cargas\(L\) y\(C\) permanecen sin cambios. Repita (a) y (b).
d) La frecuencia de la fuente se reduce a la mitad a\(\frac{1}{2}\omega _{0}\). Repita (a) y (b).
Sección 8-6
Una guía de onda rectangular metálica se llena con un plasma con ley constitutiva
\(\frac{\partial \textbf{J}_{f}}{\partial \textbf{t}}=\omega _{p}^{2}\varepsilon \textbf{E}\)
a) Encontrar las\(\textrm{TM}\) soluciones\(\textrm{TE}\) y que satisfagan las condiciones de contorno.
b) ¿Cuál es el número de onda a\(k_z\) lo largo del eje? ¿Cuál es la frecuencia de corte?
c) ¿Cuáles son las velocidades de fase y de grupo de las olas?
(d) ¿Cuál es la potencia electromagnética total que fluye por la guía de ondas para cada uno de los modos?
e) Si las paredes tienen una conductividad grande pero finita, ¿cuál es la tasa de desintegración espacial para\(\textrm{TE}_{10}\) propagar las ondas?
(a) Encontrar la potencia disipada en las paredes de una guía de ondas con conductividad grande pero finita\(\sigma _{w}\) para los\(\textrm{TM}_{mn}\) modos (Pista: Usar ecuación (25).)
b) ¿Cuál es la tasa de desintegración espacial para la propagación de ondas?
(a) Encontrar las ecuaciones de las líneas de campo eléctrico y magnético en el\(xy\) plano para los\(\textrm{TM}\) modos\(\textrm{TE}\) y.
(b) Encuentre las líneas de campo actuales de superficie en cada una de las superficies de guía de ondas para los\(\textrm{TM}_{mn}\) modos. Pista:
\(\int \tan xdx=-\ln \cos x\)
\(\int \cot xdx=\ln \sin x\)
c) Para todos los modos verificar la relación de conservación de carga en la\(x = 0\) superficie:
\(\nabla _{\sum }\cdot \textbf{K}+\frac{\partial \sigma _{f}}{\partial t}=0\)
(a) Encuentre las primeras diez frecuencias de corte más bajas si está\(a=b=1\,\textrm{cm}\) en una guía de ondas de espacio libre.
(b) ¿Cuáles son las dimensiones necesarias para que una guía de ondas cuadrada de espacio libre tenga una frecuencia de corte más baja de\(10^{10}\)\(10^{8}\),\(10^{6}\),,\(10^{4}\), o\(10^{2}\)?
Una guía de ondas rectangular de altura\(b\) y anchura\(a\) es cortocircuitada por planos perfectamente conductores en\(z=0\) y\(z=l\).
a) Encontrar la forma general de los campos\(\textrm{TM}\) eléctricos\(\textrm{TE}\) y magnéticos. (Pista: Recuerde considerar las olas viajar ing en las\(\pm z\) direcciones.)
(b) ¿Cuáles son las frecuencias naturales de este resonador?
(c) Si las paredes tienen una conductividad grande,\(\sigma _{w}\) encuentre la potencia promedio de tiempo total\(<P_d>\) disipada en el\(\textrm{TE}_{101}\) modo.
d) ¿Cuál es la energía electromagnética promedio en el tiempo total\(<W>\) almacenada en el resonador?
(e) Encontrar el\(\mathcal{Q}\) del resonador, definido como
\(\mathcal{Q}=\frac{\omega _0<W>}{<P_{d}>}\)
donde\(\omega _0\) está la frecuencia resonante.
Sección 8.7
(a) Encontrar la frecuencia crítica donde la tasa de decaimiento espacial\(\alpha \) es cero para todos los modos dieléctricos considerados.
(b) Encontrar valores aproximados de\(\alpha \),\(k_{x}\), y\(k_{z}\) para un dieléctrico muy delgado, donde\(k_{x}d\ll 1\).
(c) Para cada una de las soluciones encontrar la potencia promedio en el tiempo por unidad de longitud en cada región.
(d) Si el dieléctrico tiene una conductividad óhmica pequeña\(\sigma \), cuál es la tasa aproximada de atenuación de los campos.
Una guía de ondas dieléctrica de espesor\(d\) se coloca sobre un conductor perfecto.
(a) ¿Qué modos pueden propagarse a lo largo del dieléctrico?
b) Para cada uno de estos modos, ¿cuáles son las corrientes superficiales y las cargas del conductor?
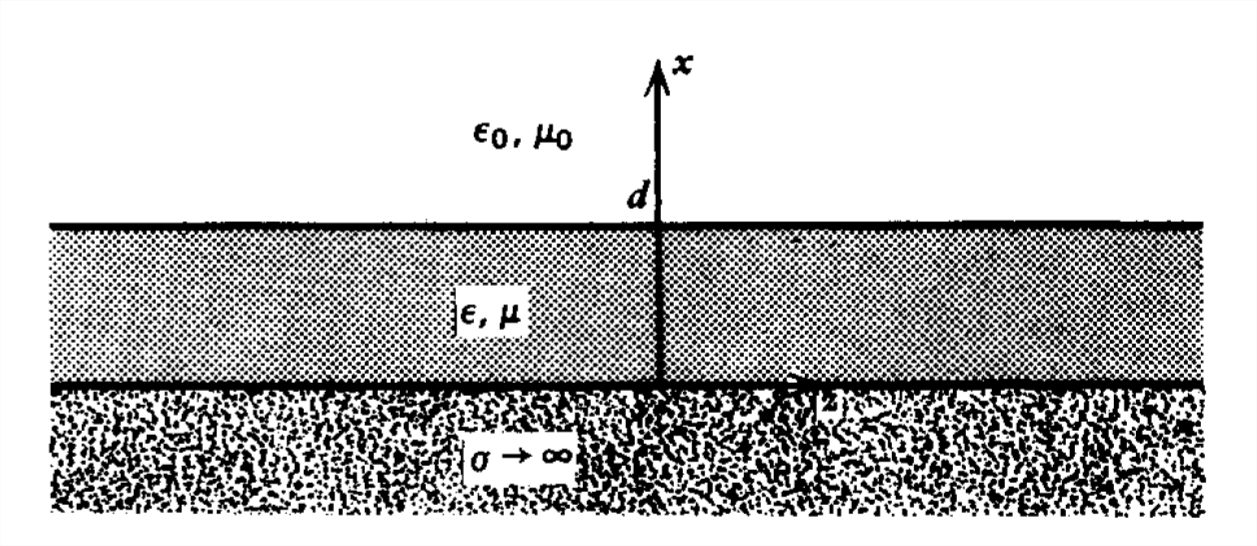
c) Verificar la relación de conservación de carga:
\(\nabla _{\sum }\cdot \textbf{K}+\frac{\partial \sigma _{f}}{\partial t}=0\)
(d) Si el conductor tiene una conductividad óhmica grande pero no infinita\(\sigma _{w}\), ¿cuál es la potencia aproximada por unidad de área disipada?
e) ¿Cuál es la tasa aproximada de atenuación de los campos?


