9.2: Radiación del dipolo puntual

El dipolo eléctrico

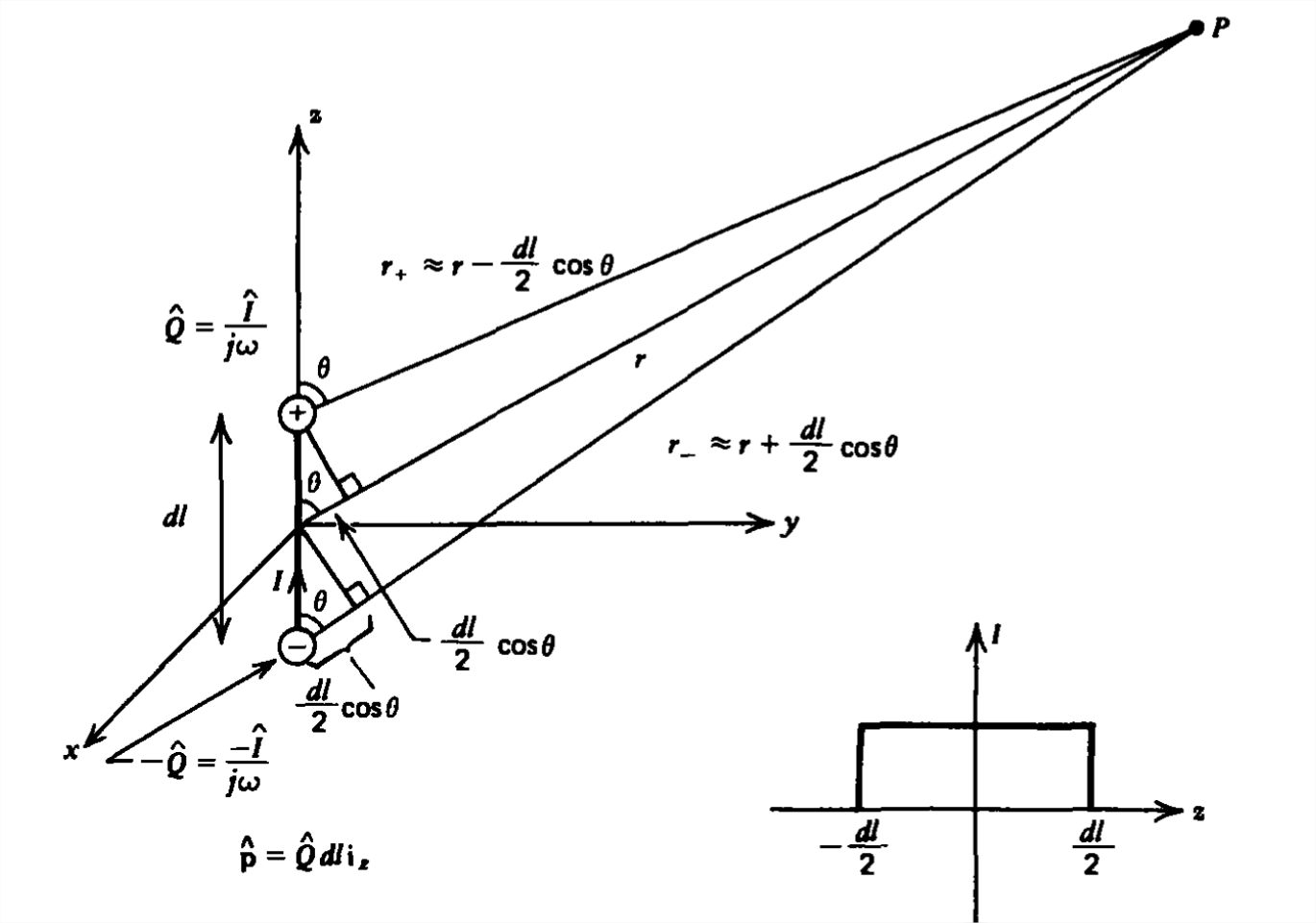
El bloque de construcción más simple para una antena transmisora es el de una corriente uniforme que fluye a lo largo de un conductor de longitud incremental\(\) dl como se muestra en la Figura 9-1. Suponemos que esta corriente varía sinusoidalmente con el tiempo como

\[  i\left ( t \right )=\textrm{Re}\left ( \hat{I}e^{j\omega t} \right ) \nonumber \]

Debido a que la corriente es discontinua en los extremos, la carga debe depositarse ahí siendo de signo opuesto en cada extremo\(\left [ q\left ( t \right )=\textrm{Re}\left ( \hat{\mathcal{Q}}e^{j\omega t} \right ) \right ]\):

\[ i\left ( t \right )=\pm \frac{dq}{dt}\Rightarrow \hat{I}=\pm j\omega \hat{\mathcal{Q}},\quad z=\pm \frac{dl}{2} \nonumber \]

Esto forma un dipolo eléctrico con el momento

\[ \textbf{p}=q\,dl\,\textbf{i}_{z} \nonumber \]

Si podemos encontrar los potenciales y campos a partir de este sencillo elemento, la solución para cualquier distribución de corriente se encuentra fácilmente por superposición.

Figura 9-1 Una antena dipolo puntual está compuesta por un cable portador de corriente distribuido uniformemente muy corto. Debido a que la corriente es discontinua en los extremos, ahí se acumulan cargas de igual magnitud pero polaridad opuesta formando un dipolo eléctrico.

Por simetría, el potencial vectorial no puede depender del ángulo\(\phi \),

\[ A_{z}=\textbf{Re}\left [ \hat{A}_{z}\left ( r,\theta  \right )e^{j\omega t} \right ] \nonumber \]

y debe estar en la misma dirección que la actual:

\[ A_{z}\left ( r,t \right )=\textrm{Re}\left [ \int_{-dl/2}^{+dl/2}\frac{\mu \hat{I}e^{j\left [ \omega \left ( t-r_{\mathcal{Q}P}/c \right ) \right ]}}{4\pi r_{\mathcal{Q}P}} dz \right ] \nonumber \]

Debido a que el dipolo es de longitud infinitesimal, la distancia desde el dipolo a cualquier punto de campo es solo la distancia radial esférica\(r\) y es constante para todos los puntos del cable corto. Entonces la integral en (5) se reduce a una multiplicación pura para producir

\[ \hat{A}_{z}=\frac{\mu \hat{I}dl}{4\pi r}e^{-jkr},\quad A_{z}\left ( r,t \right )=\textrm{Re}\left [ \hat{A}_{z}\left ( r \right )e^{j\omega t} \right ] \nonumber \]

donde nuevamente introducimos el número de onda\(k=\omega /c\) y descuidamos escribir la dependencia sinusoidal del tiempo presente en todas las cantidades de campo y fuente. Los componentes esféricos de\(\hat{A}_{z}\), son\(\left ( \textbf{i}_{z}= \textbf{i}_{r}\cos \theta -\textbf{i}_{\theta }\sin \theta  \right )\):

\[ \hat{A}_{r}=\hat{A}_{z}\cos \theta ,\quad \hat{A}_{\theta}=-\hat{A}_{z}\sin\theta ,\quad  \hat{A}_{\phi }=0 \nonumber \]

Una vez que se conoce el potencial del vector, los campos eléctrico y magnético se encuentran más fácilmente en

\ [\ hat {\ textbf {H}} =\ frac {1} {\ mu}\ nabla\ veces\ hat {\ textbf {A}},\ quad\ textbf {H}\ izquierda (r, t\ derecha) =\ textrm {Re}\ izquierda [\ hat {\ textbf {H}}\ izquierda (r,\ theta\ derecha) e^ {j\ omega t}\ derecha]\
\ sombrero {\ textbf {E}} =\ frac {1} {j\ omega\ varepsilon}\ nabla\ veces\ sombrero {\ textbf {H}},\ quad\ textbf {E}\ izquierda (r, t\ derecha) =\ textrm {Re}\ izquierda [\ hat {\ textbf {E}}\ izquierda (r,\ theta\ derecha) e^ {j\ omega t}\ derecha]\ nonumber\]

Antes de encontrar estos campos, examinemos un enfoque alternativo.

Derivación alternativa usando el potencial escalar

Fue más fácil encontrar el potencial vectorial para el dipolo eléctrico puntual debido a que la integración en (5) se redujo a una simple multiplicación. El potencial escalar se debe únicamente a las cargas puntuales opuestas en cada extremo del dipolo,

\[ \hat{V}=\frac{\mathcal{Q}}{4\pi \varepsilon }\left ( \frac{e^{-jkr_{+}}}{r_{+}}-\frac{e^{-jkr_{-}}}{r_{-}} \right ) \nonumber \]

donde\(r_{+}\) y\(r_{-}\) son las distancias desde las respectivas cargas dipolares a cualquier punto de campo, como se muestra en la Figura 9-1. Así como encontramos para el dipolo eléctrico cuasiestático en la Sección 3-1-1, no podemos dejar\(r_{+}\) e\(r_{-}\) igualar\(r\) como resultaría un potencial cero. Como mostramos en la Sección 3-1-1, se debe hacer una corrección de primer orden, donde

\ [r_ {+}\ aprox r-\ frac {dl} {2}\ cos\ theta\\
r_ {-}\ aprox r+\ frac {dl} {2}\ cos\ theta\ nonumber\]

de manera que (9) se convierte

\[ \hat{V}\approx \frac{\mathcal{Q}}{4\pi \varepsilon r}e^{-jkr}\left ( \frac{e^{jk\left ( dl/2 \right )\cos \theta }}{\left ( 1-\frac{dl}{2r}\cos \theta  \right )}-\frac{e^{-jk\left ( dl/2 \right )\cos \theta }}{\left ( 1+\frac{dl}{2r}\cos \theta  \right )} \right ) \nonumber \]

Debido a que\(dl\) se supone que la longitud del dipolo es mucho menor que la distancia de campo\(r\) y la longitud de onda, los factores de fase en los exponenciales son pequeños por lo que ellos y la\(1/r\) dependencia en los denominadores pueden expandirse en una serie Taylor de primer orden para dar como resultado:

\ begin {align}\ lim_ {k\, dl\ ll 1\\ dl/r\ ll 1}\ hat {V} &\ approx\ frac {\ mathcal {Q}} {4\ pi\ varepsilon r} e^ {-jkr}\ izquierda [\ izquierda (1+j\ frac {k\, dl} {2}\ cos\ theta\ derecha)\ izquierda (1+\ frac {dl} {2r}\ cos\ theta\ derecha) -\ izquierda (1-jk\ frac {dl} {2}\ cos\ theta\ derecha)\ izquierda (1-\ frac {dl} {2r}\ cos\ theta\ derecha)\ derecha]\ nonumber \\
&=\ frac {\ mathcal {Q} dl} {4\ pi\ varepsilon r^ {2}} e^ {-jkr}\ cos\ theta\ izquierda (1+jkr\ derecha)\ end {align}

Cuando la frecuencia se vuelve muy baja de manera que el número de onda también se vuelve pequeño, (12) se reduce al potencial dipolo eléctrico cuasiestático que se encuentra en la Sección 3-1-1 con momento dipolo\(\hat{p}=\hat{\mathcal{Q}}dl\). Sin embargo, vemos que los términos de corrección de radiación en (12) dominan a frecuencias más altas (grandes\(k\)) lejos del dipolo de\(\left (kr\gg 1  \right )\) manera que el potencial solo muere como\(1/r\) en lugar de lo cuasi-estático\(1/r^{2}\). Usando las relaciones\(\hat{\mathcal{Q}}=\hat{I}/j\omega \) y\(c=1/\sqrt{\varepsilon \mu }\), (12) podría haberse obtenido inmediatamente de (6) y (7) con la condición de calibre Lorentz de la Ec. (13) en la Sección 9-1-1:

\ [\ begin {align}\ hat {V} =\ frac {-c^ {2}} {j\ omega}\ nabla\ cdot\ hat {A} &=\ frac {-c^ {2}} {j\ omega}\ izquierda (\ frac {1} {r^ {2}}\ frac {\ parcial} {\ r parcial}\ izquierda (r^ {2}\ sombrero {A} _ {r}\ derecha) +\ frac {1} {r\ sin\ theta}\ frac {\ parcial} {\ parcial\ theta}\ izquierda (\ sombrero {A} _ {\ theta}\ sin\ theta\ derecha)\ derecha)\ nonumber\\
&=\ frac {\ mu\ hat {I} dlc^ {2}} {4\ pi j\ omega}\ frac {\ left (1+jkr\ derecha)} {r^ {2}} e^ {-jkr}\ cos\ theta\ nonumber\\
&=\ frac {\ hat {\ mathcal {Q}} dl} {4\ pi\ varepsilsilsilon en r^ {2}}\ izquierda (1+jkr\ derecha) e^ {-jkr}\ cos\ theta\ end {align}\ nonumber\]

Los campos eléctricos y magnéticos

Usando (6), los campos se encuentran directamente de (8) como

\ begin {align}\ hat {\ textbf {H}} &=\ frac {1} {\ mu}\ times\ hat {\ textbf {A}}\ nonumber\\
&=\ textbf {i} _ {\ phi}\ frac {1} {\ mu r}\ left (\ frac {\ partial} {\ partial} {\ partial}\ left (r\ hat {A} _ {\ theta}\ derecha) -\ frac {\ parcial\ hat {A} _ {r}} {\ parcial\ theta}\ derecha)\ nonumber\\
&=-\ textbf {i} _ _ {\ phi}\ frac {\ hat {I} dl} {4\ pi} k^ {2}\ sin\ theta\ izquierda (\ frac {1} {jkr} +\ frac {1} {\ izquierda (jkr\ derecha) ^ {2}}\ derecha) e^ {-jkr}\ end {align}

\ begin {align}\ hat {\ textbf {E}} &=\ frac {1} {j\ omega\ varepsilon}\ nabla\ veces\ sombrero {\ textbf {H}}\ nonumber\\
&=\ frac {1} {j\ omega\ varepsilon}\ left (\ frac {1} {r\ sin\ theta}\ frac {\ parcial} {\ parcial\ theta}\ izquierda (\ hat {H} _ {\ phi}\ sin\ theta\ derecha)\ textbf {i} _ _ {r} -\ frac {1} {r}\ frac {\ parcial} {\ parcial r}\ izquierda (r\ hat {H} _ {\ phi}\ derecha)\ textbf {i} _ {\ theta}\ derecha)\ nonumber\\
&=-\ frac {\ hat {I} dlk^ {2}} {4\ pi}\ sqrt {\ frac {\ mu} {\ varepsilon}}\ izquierda\ {\ tbf {i} _ {r}\ izquierda [2\ cos\ theta\ izquierda (\ frac {1} {\ izquierda (jkr\ derecha) ^ {2}} +\ frac {1} {\ izquierda (jkr\ derecha) ^ {3}}\ derecha)\ derecha] +\ textbf {i} _ {\ theta}\ izquierda [\ sin\ theta\ izquierda (\ frac {1} {jkr} +\ frac {1} {\ izquierda (jkr\ derecha) ^ {2}} +\ frac {1} {\ izquierda (jkr\ derecha) ^ {3}}\ derecha)\ derecha]\ derecha\} e^ {-jkr} fin {alinear}

Tenga en cuenta que incluso esta simple fuente genera un campo electromagnético bastante complicado. El campo magnético en (14) apunta puramente en la\(\phi \) dirección esperada por la regla de la derecha para una corriente\(z\) -dirigida. El término que varía como\(1/r^{2}\) se llama el campo de inducción o campo cercano para él predomina a distancias cercanas al dipolo y existe incluso a frecuencia cero. Al nuevo término, que varía como\(1/r\), se le llama campo de radiación ya que domina a distancias alejadas del dipolo y se demostrará que es responsable del flujo de potencia promedio en el tiempo que se aleja de la fuente. El término de campo cercano no contribuye al flujo de potencia sino que se debe a la energía almacenada en el campo magnético y por lo tanto resulta en potencia reactiva.

Los\(1/r^{3}\) términos en (15) son solo los términos del campo dipolo eléctrico presentes incluso a frecuencia cero y por lo tanto a menudo se les llama la solución electrostática. Predominan a distancias cercanas al dipolo y así son los campos cercanos. El campo eléctrico también tiene un campo intermedio que varía como\(1/r^{2}\), pero más importante es el término de campo de radiación en el componente io, que varía como\(1/r\). A grandes distancias domina\(\left ( kr\gg 1 \right )\) este término.

En el límite de campo lejano\(\left ( kr\gg 1 \right )\), los campos eléctrico y magnético están relacionados entre sí de la misma manera que para las ondas planas:

\[ \lim_{kr\gg 1}\hat{E}_{\theta }=\sqrt{\frac{\mu }{\varepsilon }}\hat{H}_{\phi }=\frac{\hat{E}_{0}}{jkr}\sin \theta e^{-jkr},\quad \hat{E}_{0}=-\frac{\hat{I}dlk^{2}}{4\pi }\sqrt{\frac{\mu }{\varepsilon }} \nonumber \]

Los campos eléctrico y magnético son perpendiculares y su relación es igual a la impedancia de onda\(\eta =\sqrt{\mu /\varepsilon }\). Esto es porque en el límite de campo lejano los frentes de onda esféricos se aproximan a un plano.

Líneas de Campo Eléctrico

Fuera del dipolo la densidad de carga volumétrica es cero, lo que nos permite definir un potencial de vector eléctrico\(\textbf{C}\):

\[ \nabla \cdot \textbf{E}=0\Rightarrow \textbf{E}=\nabla\times \textbf{C} \nonumber \]

Debido a que el campo eléctrico en (15) solo tiene\(r\) y\(\theta \) componentes, solo\(\textbf{C}\) debe tener un\(\phi \) componente,\(C_{\phi }\left ( r,\theta  \right )\):

\[ \textbf{E}=\nabla \times \textbf{C}=\frac{1}{r\sin \theta }\frac{\partial }{\partial \theta }\left ( \sin \theta C_{\phi } \right )\textbf{i}_{r}-\frac{1}{r}\frac{\partial }{\partial r}\left ( rC_{\phi } \right )\textbf{i}_{\theta } \nonumber \]

Seguimos el mismo procedimiento desarrollado en la Sección 4-4-3b, donde las líneas de campo eléctrico son dadas por

\[ \frac{dr}{rd\theta }=\frac{E_{r}}{E_{\theta }}=-\frac{\frac{\partial }{\partial \theta }\left ( \sin \theta C_{\phi } \right )}{\sin \theta \frac{\partial }{\partial r}\left ( rC_{\phi } \right )} \nonumber \]

que puede ser reescrito como un diferencial exacto,

\[ \frac{\partial }{\partial r}\left ( r\sin \theta C_{\phi } \right )dr+\frac{\partial }{\partial \theta }\left ( r\sin \theta C_{\phi } \right )d\theta =0\Rightarrow d\left ( r\sin \theta C_{\phi } \right )=0 \nonumber \]

de manera que las líneas de campo son solo líneas de función de flujo constante\(r\sin \theta C_{\phi }\). \(C_{\phi }\)se encuentra equiparando cada componente de vector en (18) con la solución en (15):

\ [\ begin {align}\ frac {1} {r\ sin\ theta}\ frac {\ parcial} {\ parcial\ theta}\ izquierda (\ sin\ theta\ hat {C_ {\ phi}}\ derecha) & =\ hat {E} _ _ {r} =-\ frac {\ hat {I} dlk^ {2}} {4\ pi}\ sqrt\ frac {\ mu} {\ varepsilon}}\ izquierda [2\ cos\ theta\ izquierda (\ frac {1} {\ izquierda (jkr\ derecha) ^ {2}} +\ frac {1} {\ izquierda (jkr\ derecha) ^ {3}}\ derecha)\ derecha ] e^ {-jkr} -\ frac {1} {r}\ frac {\ parcial} {\ parcial} {\ r parcial}\ izquierda (r\ hat {C_ {\ phi}}\ derecha)\ nonumber\\
&=\ hat {E} _ {\ theta} =-\ frac {\ hat {I} dlk^ {2}} {4\ pi}\ sqrt {frac {\ mu} {\ varepsilon}}\ izquierda [\ sin\ theta\ izquierda (\ frac {1} {\ izquierda (jkr\ derecha)} +\ frac {1} {\ izquierda (jkr\ derecha) ^ {2}} +\ frac {1} {\ izquierda (jkr\ izquierda (jkr\ derecha) derecha) ^ {3}}\ derecha)\ derecha] e^ {-jkr}\ end {align}\ nonumber\]

que se integra a

\[  \hat{C_{\phi }}=\frac{\hat{I}dl}{4\pi }\sqrt{\frac{\mu }{\varepsilon }}\frac{\sin \theta }{r}\left ( 1-\frac{j}{\left ( kr \right )} \right )e^{-jkr} \nonumber \]

Entonces asumiendo que\(\hat{I}\) es real, el valor instantáneo de\(C_{\phi }\) es

\ [\ begin {align} C_ {\ phi} &=\ textrm {Re}\ izquierda (\ hat {C} _ {\ phi} e^ {j\ omega t}\ derecha)\ nonumber\\
&=\ frac {\ hat {I} dl} {4\ pi}\ sqrt {\ frac {\ mu} {\ varepsilon}}\ frac {\ frac\ sin\ theta} {r}\ izquierda (\ cos\ izquierda (\ omega t-kr\ derecha) +\ frac {\ sin\ izquierda (\ omega t-kr\ derecha)} {kr}\ derecha)\ end {align}\ nonumber\]

de manera que, omitiendo el factor de amplitud constante en (23), las líneas de campo son

\[ rC_{\phi }\sin \theta =\textrm{const}\Rightarrow \sin ^{2}\theta \left ( \cos \left ( \omega t-kr \right )+\frac{\sin \left ( \omega t-kr \right )}{kr} \right )=\textrm{const} \nonumber \]

Figura 9-2 Las líneas de campo eléctrico para un dipolo eléctrico puntual en\(\omega t=0\) y\(\omega t=\pi /2\).

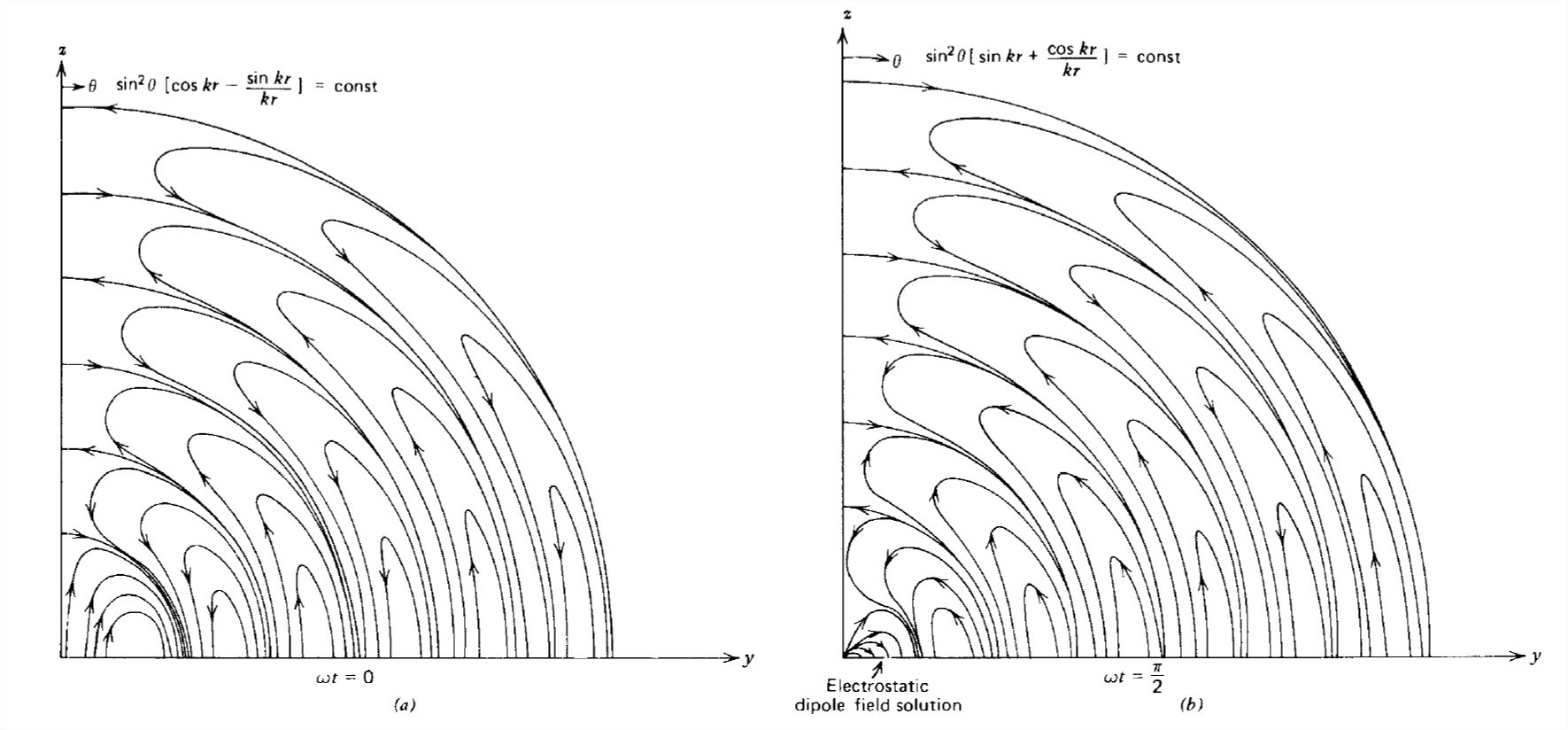
Estas líneas de campo se trazan en la Figura 9-2 a dos valores de tiempo. Podemos verificar nuestro resultado con las líneas de campo estático para un dipolo dadas en la Sección 3-1-1. Recordando que\(k=\omega /c\), a bajas frecuencias,

\ [\ lim_ {\ omega\ fila derecha 0}\ izquierda\ {\ begin {array} {lr}
\ displaystyle\ cos\ izquierda (\ omega t-kr\ derecha)\ approx 1\\
\ displaystyle\ frac {\ sin\ izquierda (\ omega t-kr\ derecha)} {kr}\ approx\ frac {\ izquierda (t-r/c\ derecha)} {r/c}\ approx\ frac {t} {r/c} -1
\ end {array}\ right. \ nonumber\]

de manera que, en el límite de baja frecuencia en un tiempo fijo, (24) se aproxima al resultado de la Ec. (6) de la Sección 3-1-1:

\[ \lim_{\omega \rightarrow 0}\sin ^{2}\theta \left ( \frac{ct}{r} \right )=\textrm{const} \nonumber \]

Obsérvese que las líneas de campo cercanas al dipolo son las de un campo de dipolo estático, como se dibuja en la Figura 3-2. En el límite de campo lejano

\[ \lim_{kr \gg  1}\sin ^{2}\theta \cos \left ( \omega t-kr \right )=\textrm{const} \nonumber \]

las líneas de campo se repiten con punto\(\lambda =2\pi /k\).

Resistencia a la Radiación

Usando los campos eléctricos y magnéticos de la Sección 9-2-3, la densidad de potencia promedio en el tiempo es

\ [\ begin {align &= <\ textbf {S} >\ frac {1} {2}\ textrm {Re}\ izquierda (\ hat {\ textbf {E}}\ veces\ hat {\ textbf {E}} ^ {\ ast}\ derecha)\ nonumber\\ & =
\ textrm {Re}\ izquierda\ {\ frac {\ izquierda |\ sombrero {I} dl derecha |^ {2}\ eta k^ {4}} {2\ izquierda (4\ pi\ derecha) ^ {2}}\ izquierda [-\ textbf {i} _ {\ theta}\ sin 2\ theta\ izquierda (-\ frac {1} {\ izquierda (jkr\ derecha) ^ {3}} +\ frac {1} {\ izquierda (jkr\ derecha) ^ {5}}\ derecha)\ derecha] +\ textbf {i} _ {r}\ sin ^ {2}\ theta\ izquierda (-\ frac {1} {\ izquierda (jkr\ derecha) ^ {2}} +\ frac {1} {izquierda\ (jkr\ derecha) ^ {5}}\ derecha)\ derecha\}\ nonumber\\ &
=\ frac {1} {2}\ izquierda |\ hat {I} dl\ derecha |^ {2}\ izquierda (\ frac {k} {4\ pi}\ derecha) ^ { 2}\ frac {\ eta} {r^ {2}}\ sin^ {2}\ theta\ textbf {i} _ {r}\ nonumber\\ &
=\ frac {1} {2}\ frac {\ izquierda |\ sombrero {E} _ {0}\ derecha |^ {2}} {\ eta}\ frac {\ sin ^ {2}\ theta} {\ izquierda (kr\ derecha) ^ {2}}\ textbf {i} _ {r}\ end {align}\ nonumber\]

donde\(\hat{E}_{0}\) se define en (16).

Solo los campos lejanos contribuyeron al flujo de potencia promedio en el tiempo. Los campos cercanos e intermedios aportaron solo términos imaginarios en (28) que representan la potencia reactiva.

La densidad de potencia varía con el ángulo\(\theta \), siendo cero a lo largo del eje del dipolo eléctrico\(\left ( \theta =0,\pi  \right )\) y máxima en ángulo recto con él\(\left ( \theta =\pi /2 \right )\), ilustrada por el patrón de potencia de radiación en la Fig. 9-3. La fuerza de la densidad de potencia es proporcional a la longitud del vector desde el origen hasta el

Figura 9-3 La intensidad del campo eléctrico y la densidad de potencia debida a un dipolo puntual\(z\) dirigido en función del ángulo\(\theta \) es proporcional a la longitud del vector desde el origen hasta el patrón de radiación.

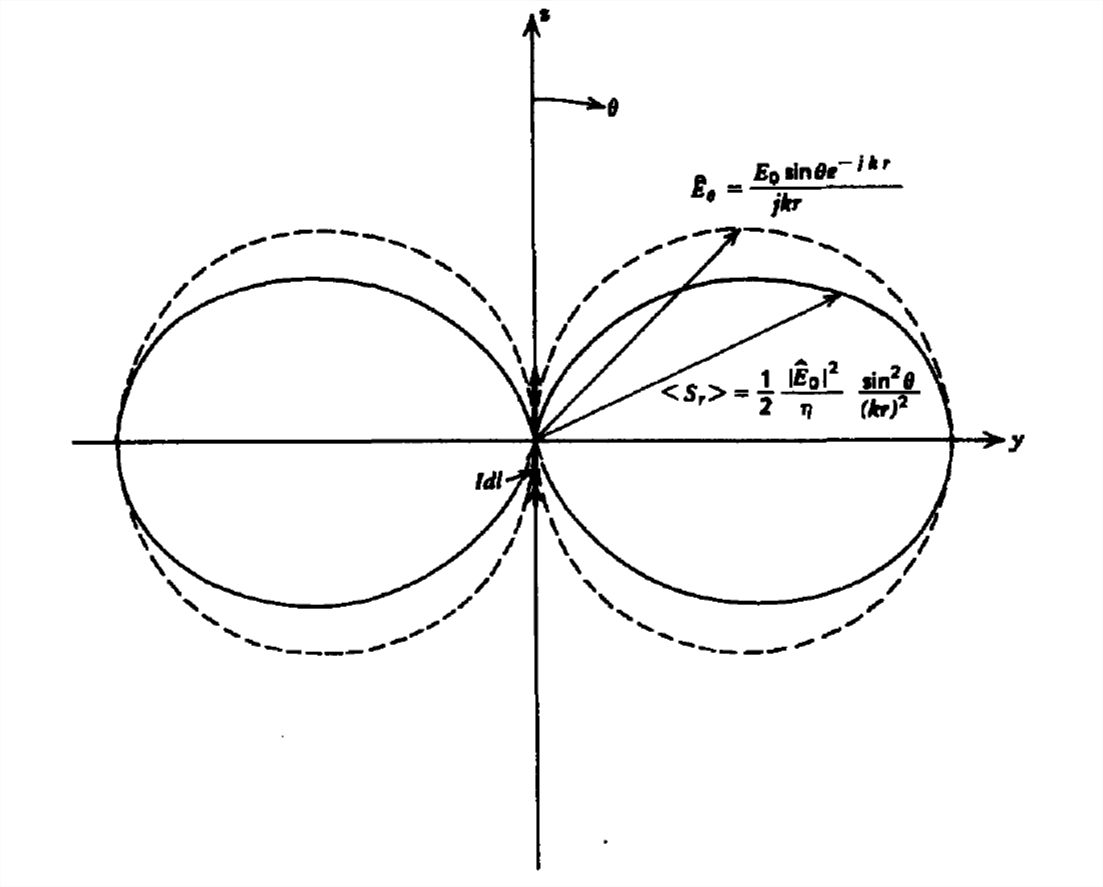
patrón de radiación. Estas propiedades direccionales son útiles en la dirección del haz, donde se pueden controlar las direcciones de la fila de potencia.

La potencia promedio en el tiempo total irradiada por el dipolo eléctrico se encuentra integrando el vector Poynting sobre una superficie esférica en cualquier radio\(r\):

\[ \begin{align} <P>&=\int_{\theta =0}^{\pi }\int_{\phi =0}^{2\pi }<S_{r}>r^{2}\sin \theta d\theta d\phi \nonumber \\ & =\frac{1}{2}\left | \hat{I}dl \right |^{2}\left ( \frac{k}{4\pi } \right )^{2}\eta 2\pi \int_{\theta =0}^{\pi }\sin ^{3}\theta d\theta \nonumber \\ & =\frac{\left | \hat{I}dl \right |^{2}}{16\pi }\eta k^{2}\left [ -\frac{1}{3}\cos \theta \left ( \sin ^{2}\theta +2 \right ) \right ]\bigg|_{0}^{\pi }\nonumber \\ & =\frac{\left | \hat{I}dl \right |^{2}}{12\pi }\eta k^{2} \end{align} \nonumber \]

En lo que respecta al dipolo, esta potencia radiada se pierde de la misma manera que si se disipara en una resistencia\(R\),

\[ <P>=\frac{1}{2}\left | \hat{I} \right |^{2}R \nonumber \]

donde esta resistencia equivalente se llama resistencia a la radiación:

\[ R=\frac{\eta }{6\pi }\left ( k\,dl \right )^{2}=\frac{2\pi \eta }{3}\left ( \frac{dl}{\lambda } \right )^{2},\quad k=\frac{2\pi }{\lambda } \nonumber \]

En el espacio libre\(\eta _{0}=\sqrt{\mu _{0}/\varepsilon _{0}}\approx 120\pi \), la resistencia a la radiación es

\[ R_{0}=80\pi^{2}\left ( \frac{dl}{\lambda} \right )^{2}\quad \left ( \textrm{free space} \right ) \nonumber \]

Estos resultados sólo son ciertos para dipolos puntuales, donde\(dl\) es mucho menor que una longitud de onda\(\left ( dl/\lambda \ll 1 \right )\). Esto verifica la validez de la aproximación cuasiestática para geometrías mucho más pequeñas que una longitud de onda radiada, ya que la potencia radiada es entonces insignificante.

Si la corriente en un dipolo no es constante sino que varía con\(z\) la longitud, el único término con el que varía\(z\) para el potencial vectorial en (5) es\(\hat{I}\left ( z \right )\):

\[ \hat{A}_{z}\left ( r \right )=\textrm{Re}\left [ \int_{-dl/2}^{+dl/2}\frac{\mu \hat{I}\left ( z \right )e^{-jkr_{\mathcal{Q}P}}}{4\pi r_{\mathcal{Q}P}}dz \right ]\approx \textrm{Re}\left [ \frac{\mu e^{-jkr_{\mathcal{Q}P}}}{4\pi r_{\mathcal{Q}P}}\int_{-dl/2}^{+dl/2}\hat{I}\left ( z \right )dz \right ]  \nonumber \]

donde, debido a que el dipolo es de longitud infinitesimal, la distancia\(r_{\mathcal{Q}P}\) desde cualquier punto del dipolo a cualquier punto de campo lejos del dipolo es esencialmente\(r\), independiente de\(z\). Entonces, todos los resultados adicionales para los campos eléctrico y magnético son los mismos que en la Sección 9-2-3 si reemplazamos la longitud real del dipolo\(dl\) por su longitud efectiva,

\[ dl_{\textrm{eff}}=\frac{1}{\hat{I}_{0}}\int_{-dl/2}^{+dl/2}\hat{I}\left ( z \right )dz \nonumber \]

donde\(\hat{I}_{0}\) está la corriente terminal que alimenta el centro del dipolo.

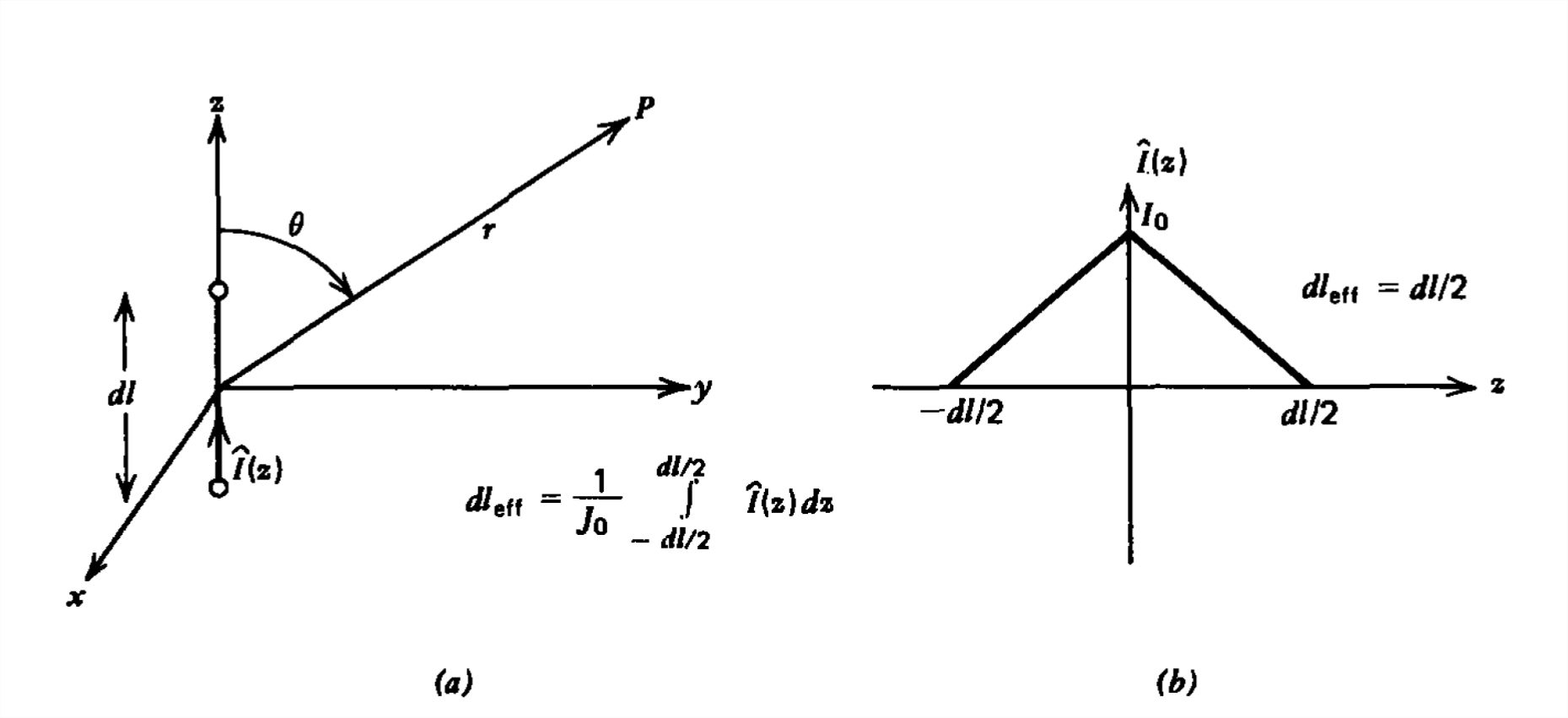
Generalmente la corriente es cero en los extremos de circuito abierto, como para la distribución lineal mostrada en la Figura 9-4,

\ [\ hat {I}\ left (z\ right) =\ left\ {\ begin {array} {ll}
\ displaystyle I_ {0}\ left (1-2z/dl\ right),\ quad 0\ leq z\ leq dl/2\
\ displaystyle I_ {0}\ left (1-2z/dl\ right),\ quad -dl/2\ leq z\ leq 0
\ end {array}\ derecho. \ nonumber\]

para que la longitud efectiva sea la mitad de la longitud real:

\[ dl_{\textrm{eff}}=\frac{1}{I_{0}}\int_{-dl/2}^{+dl/2}\hat{I}\left ( z \right )dz=\frac{dl}{2} \nonumber \]

Figura 9-4 (a) Si un dipolo eléctrico puntual tiene una distribución de corriente no uniforme, las soluciones son de la misma forma si reemplazamos la longitud real del dipolo\(dl\) por una longitud efectiva\(dl_{\textrm{eff}}\). b) Para una distribución triangular de corriente, la longitud efectiva es la mitad de la longitud verdadera.

Debido a que los campos se reducen a la mitad, la resistencia a la radiación se reduce en:

\[ R=\frac{2\pi \eta }{3}\left ( \frac{dl_{\textrm{eff}}}{\lambda } \right )^{2}=20\pi ^{2}\sqrt{\frac{\mu _{r}}{\varepsilon _{r}}}\left ( \frac{dl}{\lambda } \right )^{2} \nonumber \]

En el espacio libre la permeabilidad relativa\(\mu _{r}\) y la permitividad relativa\(\varepsilon _{r}\) son unidad.

Tenga en cuenta también que con una distribución de corriente espacialmente dependiente, se encuentra una distribución de carga de línea en toda la longitud del dipolo y no solo en los extremos:

\[ \hat{\lambda }=-\frac{1}{j\omega }\frac{d\hat{I}}{dz} \nonumber \]

Para la distribución lineal de corriente descrita por (35), vemos que:

\ [\ hat {\ lambda} =\ pm\ frac {2I_ {0}} {j\ omega dl}\ izquierda\ {\ comenzar {matriz}
0\ leq z\ leq dl/2\\
-dl/2\ leq z\ leq 0
\ end {matriz}\ derecha. \ nonumber\]

Rayleigh Scattering (¿o por qué el cielo es azul?)

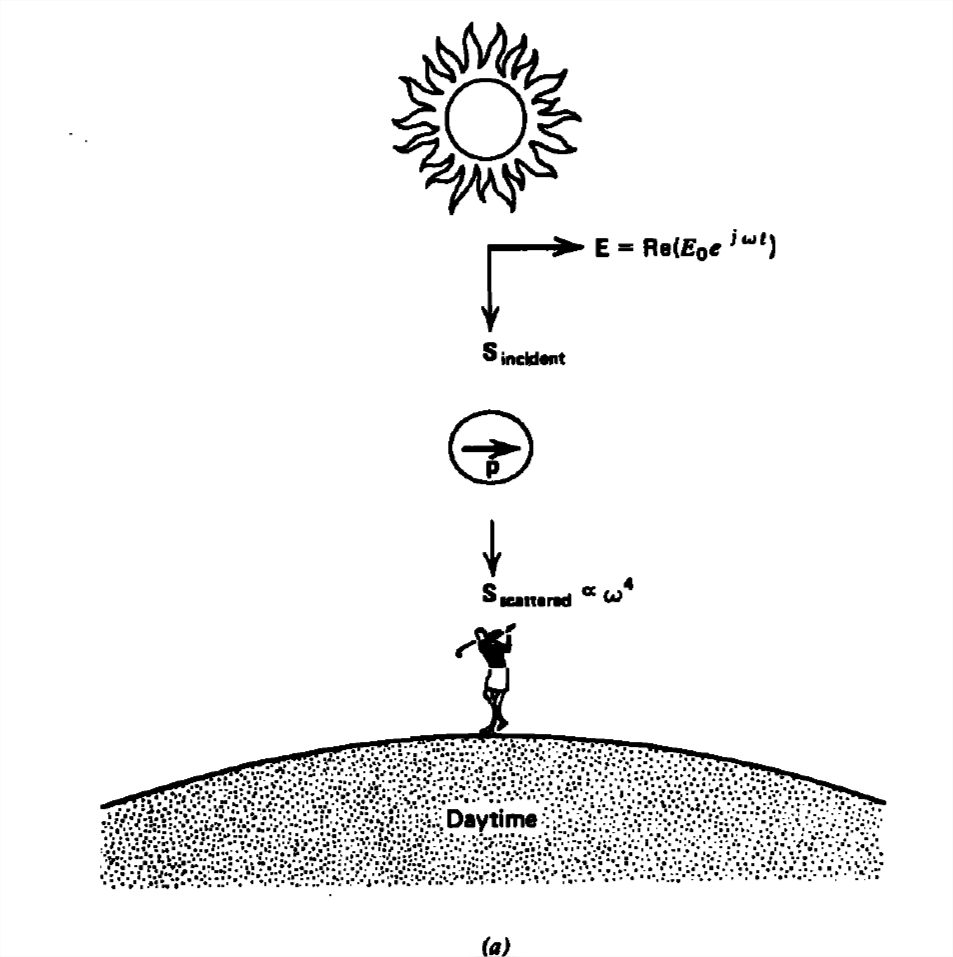
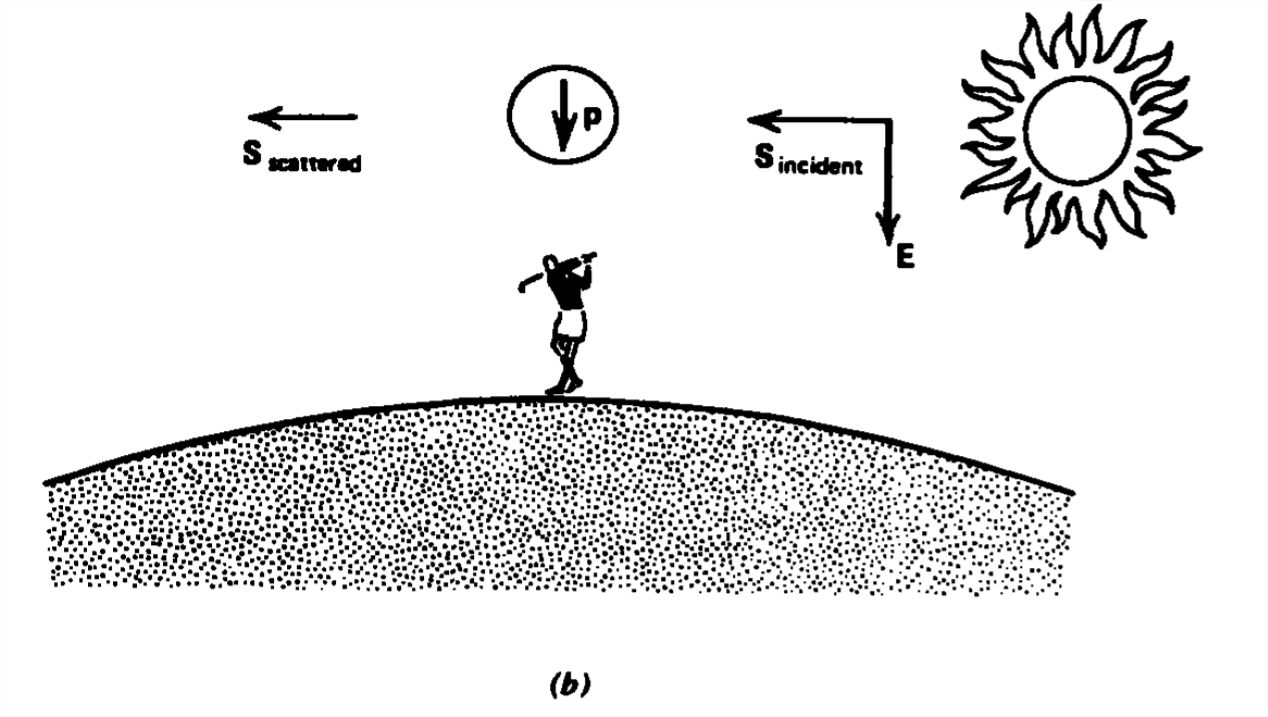
Si un campo\(\textrm{Re}\left [ E_{0}e^{j\omega t} \textbf{i}_{x}\right ]\) eléctrico de onda plana incide sobre un átomo que es mucho más pequeño que la longitud de onda, el momento dipolar inducido también contribuye al campo resultante, como se ilustra en la Figura 9-5. El poder disperso es perpendicular al momento dipolar inducido. Utilizando el modelo de dipolo desarrollado en la Sección 3-1-4, donde una nube de electrones esféricos negativos de radio\(R_{0}\) con carga total\(-\mathcal{Q}\) rodea a un

Figura 9-5 Un campo eléctrico incidente polariza dipolos que luego vuelven a irradiar su energía principalmente perpendicular al campo eléctrico polarizador. La potencia dispersa promedio en el tiempo aumenta con la cuarta potencia de frecuencia, por lo que las longitudes de onda más cortas de la luz se dispersan más que las longitudes de onda más largas. (a) Durante el día un observador de la Tierra ve más luz azul dispersada por lo que el cielo se ve azul (longitudes de onda cortas). (b) Cerca del atardecer la luz que llega al observador carece de azul por lo que el cielo aparece rojizo (longitud de onda larga).

núcleo de punto positivo, la ley de Newton para la nube cargada con masa\(m\) es:

\[ \frac{d^{2}x}{dt^{2}}+\omega _{0}^{2}x=\textrm{Re}\left ( \frac{\mathcal{Q}E_{0}}{m}e^{j\omega t} \right ),\quad \omega _{0}^{2}=\frac{\mathcal{Q}^{2}}{4\pi \varepsilon mR_{0}^{3}} \nonumber \]

El momento dipolo resultante es entonces

\[  \hat{p}=\mathcal{Q}\hat{x}=\frac{\mathcal{Q}^{2}E_{0}/m}{\omega_{0}^{2}-\omega^{2}} \nonumber \]

donde descuidamos los efectos de amortiguación. Este dipolo luego se vuelve a irradiar con soluciones dadas en las Secciones 9-2-1-9-2-5 utilizando el momento dipolar de (41)\(\left ( \hat{I}dl\rightarrow j\omega\hat{p} \right )\). La potencia promedio en el tiempo total irradiada se encuentra a partir de (29) como

\[ <P>=\frac{\omega ^{4}\left | \hat{p} \right |^{2}\eta }{12\pi c^{2}}=\frac{\omega ^{4}\eta \left ( \mathcal{Q}^{2}E_{0}/m\right )^{2}}{12\pi c^{2}\left ( \omega _{0}^{2}-\omega ^{2} \right )^{2}} \nonumber \]

Para calcular aproximadamente\(\omega _{0}\), utilizamos el radio aproximado del electrón que se encuentra en la Sección 3-8-2 equiparando la energía almacenada en la fórmula relativista de Einstein que relaciona la masa con la energía:

\[ mc^{2}=\frac{3Q^{2}}{20\pi \varepsilon R_{0}}\Rightarrow R_{0}=\frac{3Q^{2}}{20\pi \varepsilon mc^{2}}\approx 1.69\times 10^{-15}m  \nonumber \]

Luego de (40)

\[ \omega _{0}=\frac{\sqrt{5/3}20\pi \varepsilon mc^{2}}{3\mathcal{Q}^{2}}\approx 2.3\times 10^{23}\,\textrm{radian/sec} \nonumber \]

es mucho mayor que las frecuencias de luz de\(\left ( \omega \approx 10^{15} \right )\) manera que (42) se vuelve aproximadamente

\[ \lim_{\omega _{0}\gg \omega }<P>\approx \frac{\eta }{12\pi }\left ( \frac{\mathcal{Q}^{2}E_{0}\omega ^{2}}{mc\omega _{0}^{2}} \right )^{2} \nonumber \]

Este resultado fue derivado originalmente por Rayleigh para explicar el azulado del cielo. Dado que la potencia dispersa es proporcional a\(\omega ^{4}\), domina la luz de longitud de onda más corta. Sin embargo, cerca del atardecer la luz se dispersa paralela a la tierra más que hacia ella. La luz azul recibida por un observador en la tierra disminuye de manera que las longitudes de onda más largas dominan y el cielo aparece rojizo.

Radiación de un dipolo magnético puntual

Un bucle cerrado de corriente sinusoidalmente variable de tamaño muy pequeño que fluye en el\(z = 0\) plano también genera ondas radiantes. Debido a que el bucle está cerrado, la corriente no tiene divergencia por lo que no hay carga y el potencial escalar es cero. La amplitud del fasor potencial del vector es entonces

\[ \hat{\textbf{A}}\left ( r \right )=\int \frac{\mu \hat{\textbf{I}}e^{-jkr_{\mathcal{Q}P}}}{4\pi r_{\mathcal{Q}P}}dl \nonumber \]

Asumimos que el dipolo es mucho más pequeño que una longitud de onda\(k\left ( r_{\mathcal{Q}P}-r\right )\ll 1\), de modo que el factor exponencial en (46) puede linealizarse para

\[ \lim_{k\left ( r_{\mathcal{Q}P}-r \right )\ll 1}e^{-jkr_{\mathcal{Q}P}}=e^{-jkr}e^{-jk\left ( r_{\mathcal{Q}P}-r \right )}\approx e^{-jkr}\left [ 1-jk\left ( r_{\mathcal{Q}P}-r \right ) \right ] \nonumber \]

Entonces (46) reduce a

\[ \begin{align} \hat{\textbf{A}}\left ( r \right )&=\int \frac{\mu \hat{\textbf{I}}}{4\pi }e^{-jkr}\left ( \frac{1+jkr}{r_{\mathcal{Q}P}} -jk\right )dl\nonumber \\ & =e^{-jkr}\int \frac{\mu \hat{\textbf{I}}}{4\pi }\left ( \frac{1+jkr}{r_{\mathcal{Q}P}} -jk\right )dl\nonumber \\ &=\frac{\mu}{4\pi }e^{-jkr}\left ( \left ( 1+jkr \right )\int \frac{\hat{\textbf{I}}dl}{r_{\mathcal{Q}P}}-jk\int \hat{\textbf{I}}dl \right ) \end{align} \nonumber \]

donde todos los términos de los que dependen\(r\) pueden tomarse fuera de las integrales porque\(r\) es independiente de\(dl\). La segunda integral es cero porque la corriente vectorial tiene magnitud constante y fluye en un bucle cerrado de manera que su dirección promedio integrada sobre el bucle es cero. Esto se ve más fácilmente con un bucle rectangular donde lados opuestos del bucle aportan igual magnitud pero signos opuestos a la integral, que así suma a cero. Si el bucle es circular con radio\(a\),

\[ \hat{\textbf{I}}dl=\hat{I}\textbf{i}_{\phi }ad\phi \Rightarrow \int_{0}^{2\pi }\textbf{i}_{\phi }d\phi =\int_{0}^{2\pi }\left ( -\sin \phi \textbf{i}_{x}+\cos \phi \textbf{i}_{y} \right )d\phi =0 \nonumber \]

la integral vuelve a ser cero ya que el valor promedio del vector unitario\(\textbf{i}_{\phi }\) alrededor del bucle es cero.

La integral restante es la misma que para los cuasi-estáticos salvo que se multiplica por el factor\(\left ( 1+jkr \right )e^{-jkr}\). Usando los resultados de la Sección 5-5-1, el potencial vectorial cuasiestático también se multiplica por esta cantidad:

\[ \hat{\textbf{A}}=\frac{\mu \hat{m}}{4\pi r^{2}}\sin \theta \left ( 1+jkr \right )e^{-jkr}\textbf{i}_{\phi },\quad \hat{m}=\hat{I}dS \nonumber \]

Los campos eléctricos y magnéticos son entonces

\ [\ hat {\ textbf {H}} =\ frac {1} {\ mu}\ nabla\ veces\ hat {\ textbf {A}} =-\ frac {\ hat {m}} {4\ pi} jk^ {3} e^ {-jkr}\ left\ {\ textbf {i} _ {r}\ left [2\ cos\ theta\ izquierda (\ frac {1} {\ izquierda (jkr\ derecha) ^ {2}} +\ frac {1} {\ izquierda (jkr\ derecha) ^ {3}}\ derecha)\ derecha] +\ textbf {i} _ {\ theta}\ izquierda [\ sin\ theta\ izquierda (\ frac {1} {jkr} +\ frac {1} { izquierda (jkr\ derecha) ^ {2}} +\ frac {1} {\ izquierda (jkr\ derecha) ^ {3}}\ derecha)\ derecha]\ derecha\}\
\ sombrero {\ textbf {E}} =\ frac {1} {j\ omega\ varepsilon}\ nabla\ veces\ sombrero {\ textbf {H}} =\ frac {\ hat {m} jk^ {3}} {4\ pi}\ eta e^ {-jkr}\ sin\ theta\ izquierda (\ frac {1} {jkr} +\ frac {1} {\ izquierda (jkr\ derecha) ^ {2}}\ derecha)\ textbf {i} _ _ {\ phi}\ nonumber\]

Las soluciones de campo dipolo magnético son las duales a las del dipolo eléctrico donde los campos eléctrico y magnético invierten papeles si reemplazamos el momento dipolo eléctrico por el momento dipolo magnético:

\[ \frac{\textbf{p}}{\varepsilon }=\frac{q\textbf{dl}}{\varepsilon }=\frac{\textbf{I}dl}{j\omega \varepsilon }\rightarrow \textbf{m} \nonumber \]