9.3: Matrices de dipolos puntuales

La densidad de potencia para un dipolo eléctrico puntual varía con la distribución angular amplia\(\sin ^{2}\theta \). A menudo se desea que el patrón de potencia sea altamente directivo con ciertos ángulos que lleven la mayor parte de la potencia con una densidad de potencia insignificante en otros ángulos. También es necesario que las direcciones para el flujo de potencia máximo sean controlables sin movimiento mecánico de la antena. Estos requisitos pueden cumplirse mediante el uso de más dipolos en una matriz periódica.

Una simple matriz de dos elementos

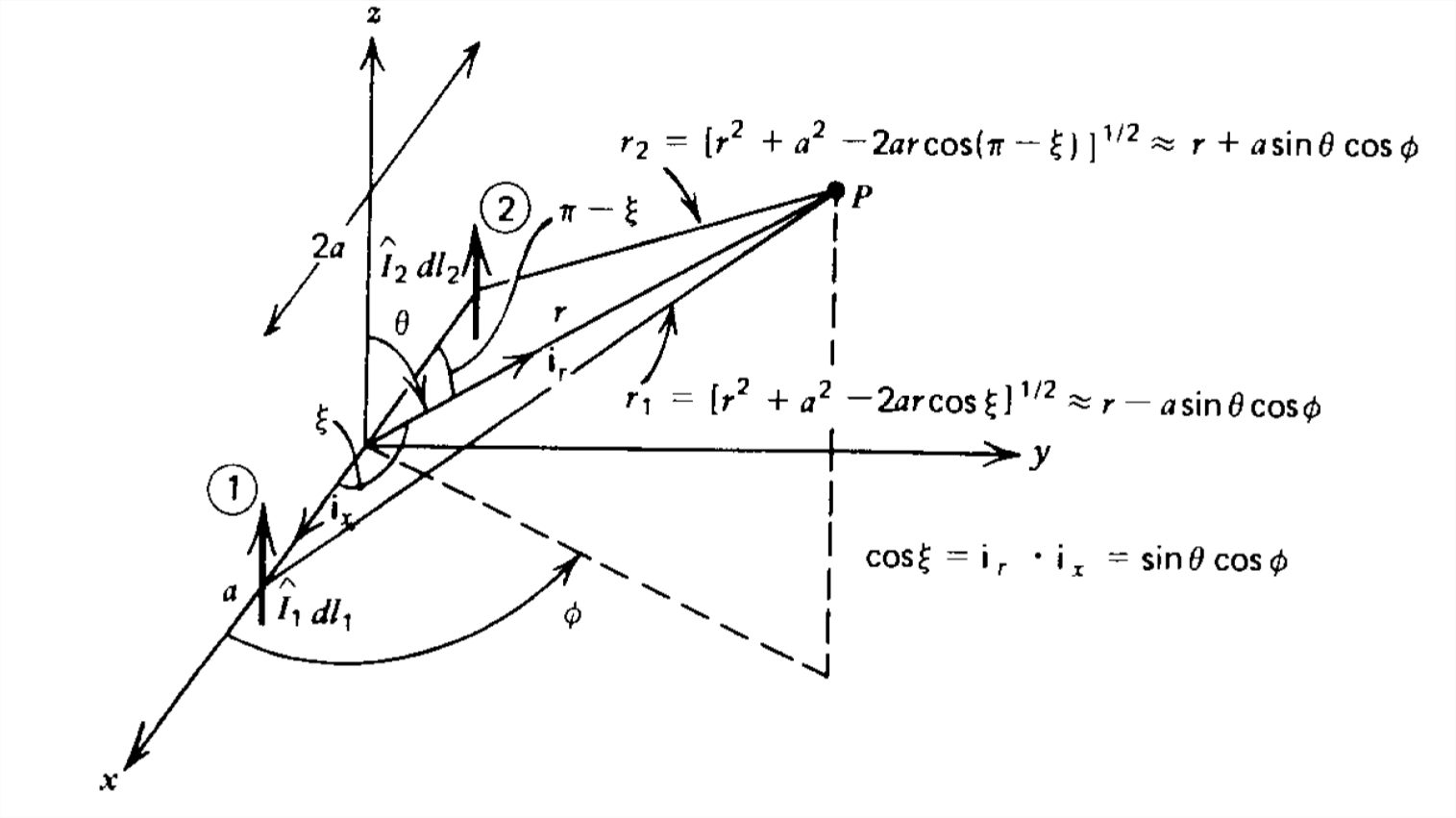
Para ilustrar los principios básicos de las matrices de antenas, consideramos la matriz de dipolos eléctricos de dos elementos que se muestra en la Figura 9-6. Suponemos que cada elemento lleva corrientes uniformes\(\hat{I}_{1}\) y\(\hat{I}_{2}\) y tiene longitudes\(dl_{1}\) y\(dl_{2}\), respectivamente. Los elementos están a una distancia de\(2a\) distancia. Los campos en cualquier punto\(P\) vienen dados por la superposición de campos debido a cada dipolo solo. Ya que solo nos interesa el patrón de radiación de campo lejano donde\(\theta _{1}\approx \theta _{2}\approx \theta \), utilizamos las soluciones de la Ec. (16) en la Sección 9-2-3 para escribir:

\[\hat{E}_{\theta }=\eta \hat{H}_{\phi }=\frac{\hat{E}_{1}\sin \theta e^{-jkr_{1}}}{jkr_{1}}+\frac{\hat{E}_{2}\sin \theta e^{-jkr_{2}}}{jkr_{2}} \nonumber \]

donde

\(\hat{E}_{1}=-\frac{\hat{I}_{1}dl_{1}k^{2}}{4\pi }\eta ,\quad \hat{E}_{2}=-\frac{\hat{I}_{2}dl_{2}k^{2}\eta }{4\pi }\)

Figura 9-6 El campo en cualquier punto\(P\) debido a dipolos de dos puntos es solo la suma de los campos debido a cada dipolo solo tomando en cuenta la diferencia en distancias a cada dipolo.

Recuerden, podemos superponer los campos pero no podemos superponer los flujos de poder.

De la Ley de Cosinos las distancias\(r_{1}\), y\(r_{2}\) se relacionan como

\ [\ begin {align} r_ {2} &=\ izquierda [r^ {2} +a^ {2} -2ar\ cos\ izquierda (\ pi -\ xi\ derecha)\ derecha] ^ {1/2} =\ izquierda [r^ {2} +a^ {2} +2ar\ cos\ xi\ derecha] ^ {1/2}\ nonumber\\
r_ {1} &= izquierda\ [r^ {2} +a^ {2} -2ar\ cos\ xi\ derecha] ^ {1/2}\ end {align}\ nonumber\]

donde\(\xi\) es el ángulo entre el vector radial unitario\(\textbf{i}_{r}\) y el\(x\) eje:

\( \cos \xi =\textbf{i}_{r}\cdot \textbf{i}_{x}=\sin \theta \cos \phi \)

Dado que estamos interesados en el patrón de campo lejano, linealizamos (2) a

\ [\ lim_ {r\ gg a}\ izquierda\ {\ comenzar {matriz}
\ displaystyle r_ {2}\ aprox r\ izquierda [1+\ frac {1} {2}\ izquierda (\ frac {a^ {2}} {r^ {2}} +\ frac {2a} {r}\ sin\ theta\ cos\ phi\ derecha]\ aprox r+a\ sin\ theta\ cos\ phi\\
\ displaystyle r_ {1}\ aprox r\ izquierda [1+\ frac {1} {2}\ izquierda (\ frac {a^ {2}} {r^ {2}} -\ frac {2a} {r}\ sin\ theta\ cos\ phi\ derecha)\ derecha]\ approx r-a\ sin\ theta\ cos\ phi
\ fin {matriz}\ derecha. \ nonumber\]

En este límite de campo lejano, los términos de corrección tienen poco efecto en los denominadores de (1) pero pueden tener un efecto significativo en los factores de fase exponenciales si\(a\) es comparable a una longitud de onda para que\(ka\) sea cercana o mayor que la unidad. En este espíritu incluimos los términos de corrección de primer orden de (3) en los factores de fase de (1), pero no en ningún otro lugar, de manera que (1) se reescribe como

\ [\ begin {align}\ hat {E} _ {\ theta} &=\ eta\ hat {H} _ {\ phi}\ nonumber\\ &
=\ underset {\ textrm {elemento facotr}} {\ underbrackets {\ frac {jk\ eta} {4\ pi r}\ sin\ theta e^ {-jkr}}\ underset {\ textrm {factor de matriz}} {\ underbrackets {\ left (\ hat {I} _ {1} dl_ {1} e^ {jka\ sin\ theta\ cos\ phi} +\ hat {I} _ {2} dl_ {2} e^ {-jka\ sin \ theta\ cos\ phi}\ derecha)}}\ end {align}\ nonumber\]

El primer factor se llama factor elemento porque es el campo de radiación por unidad de elemento de corriente\(\left ( \hat{I}dl \right )\) debido a un solo dipolo en el origen. El segundo factor se llama factor array porque solo depende de la geometría y excitaciones (magnitud y fase) de cada elemento dipolo de la matriz.

Para examinar (4) con mayor detalle, asumimos que los dos dipolos son idénticos en longitud y que las corrientes tienen la misma magnitud pero pueden diferir en fase\(\mathcal{X}\):

\ [dl_ {1} =dl_ {2}\ equiv dl\
\ hat {I} _ {1} =\ hat {I},\ quad\ hat {I} _ {2} =\ hat {I} e^ {j\ mathcal {X}}\ Rightarrow\ hat {E} _ _ {1} =\ hat {E} _ {0},\ quad\ hat {E} _ {2} =\ sombrero {E} _ {0} e^ {j\ mathcal {X}}\ nonumber\]

para que (4) pueda escribirse como

\[ \hat{E}_{\theta }=\eta \hat{H}_{\phi }=\frac{2\hat{E}_{0}}{jkr}e^{-jkr}\sin \theta e^{j\mathcal{X}/2}\cos \left ( ka\sin \theta \cos \phi -\frac{\mathcal{X}}{2} \right ) \nonumber \]

Ahora los campos lejanos también dependen de\(\phi \). En particular, enfocamos la atención en el\(\theta =\pi /2\) plano. Luego el flujo de energía,

\[ \lim_{\theta =\pi /2}<S_{r}>=\frac{1}{2\eta }\left | \hat{E}_{\theta} \right |^{2}=\frac{2\left | \hat{E}_{0} \right |^{2}}{\eta \left ( kr \right )^{2}}\cos ^{2}\left ( ka\cos \phi -\frac{\mathcal{X}}{2} \right ) \nonumber \]

depende en gran medida del espaciado dipolar\(2a\) y de la diferencia de fase de corriente\(\mathcal{X}\).

(a) Matriz Broadside

Consideremos el caso donde las corrientes están en fase\(\left ( \mathcal{X}=0 \right )\) pero el espaciamiento dipolar es de media longitud de onda\(\left ( 2a=\lambda /2 \right )\). Entonces, como lo ilustra el patrón de radiación en la Figura 9-7a, las intensidades de campo se cancelan a lo largo del\(x\) eje mientras se suman a lo largo del\(y\) eje. Esto se debe a que a lo largo del\(y\) eje\(r_{1}=r_{2}\), por lo que los campos debidos a cada dipolo se suman, mientras que a lo largo del\(x\) eje las distancias difieren en media longitud de onda para que los campos dipolares cancelen. Dondequiera que la fase del factor de matriz\(\left ( ka\cos \phi -\mathcal{X}/2 \right )\) sea un múltiplo entero de\(\pi \), la densidad de potencia es máxima, mientras que donde sea un múltiplo entero impar de\(\pi /2\), la densidad de potencia es cero. Debido a que este patrón de radiación es máximo en la dirección perpendicular a la matriz, se llama patrón de lado ancho.

Figura 9-7 El patrón de radiación de potencia debido a los dipolos de dos puntos depende fuertemente del espaciamiento de dipolos y de las fases de corriente. Con un espaciado dipolar de media longitud de onda\(\left ( 2a=\lambda /2 \right )\), el patrón de radiación se dibuja para varios valores de diferencia de fase actual en el\(\theta =\pi /2\) plano. La matriz de lado ancho en (a) con las corrientes en fase\(\left ( \mathcal{X}=0 \right )\) tiene el lóbulo de potencia en la dirección perpendicular a la matriz, mientras que la matriz de fin de disparo en (e) tiene corrientes fuera de fase\(\left ( \mathcal{X}= \pi \right )\) con el lóbulo de potencia en la dirección a lo largo de la matriz.

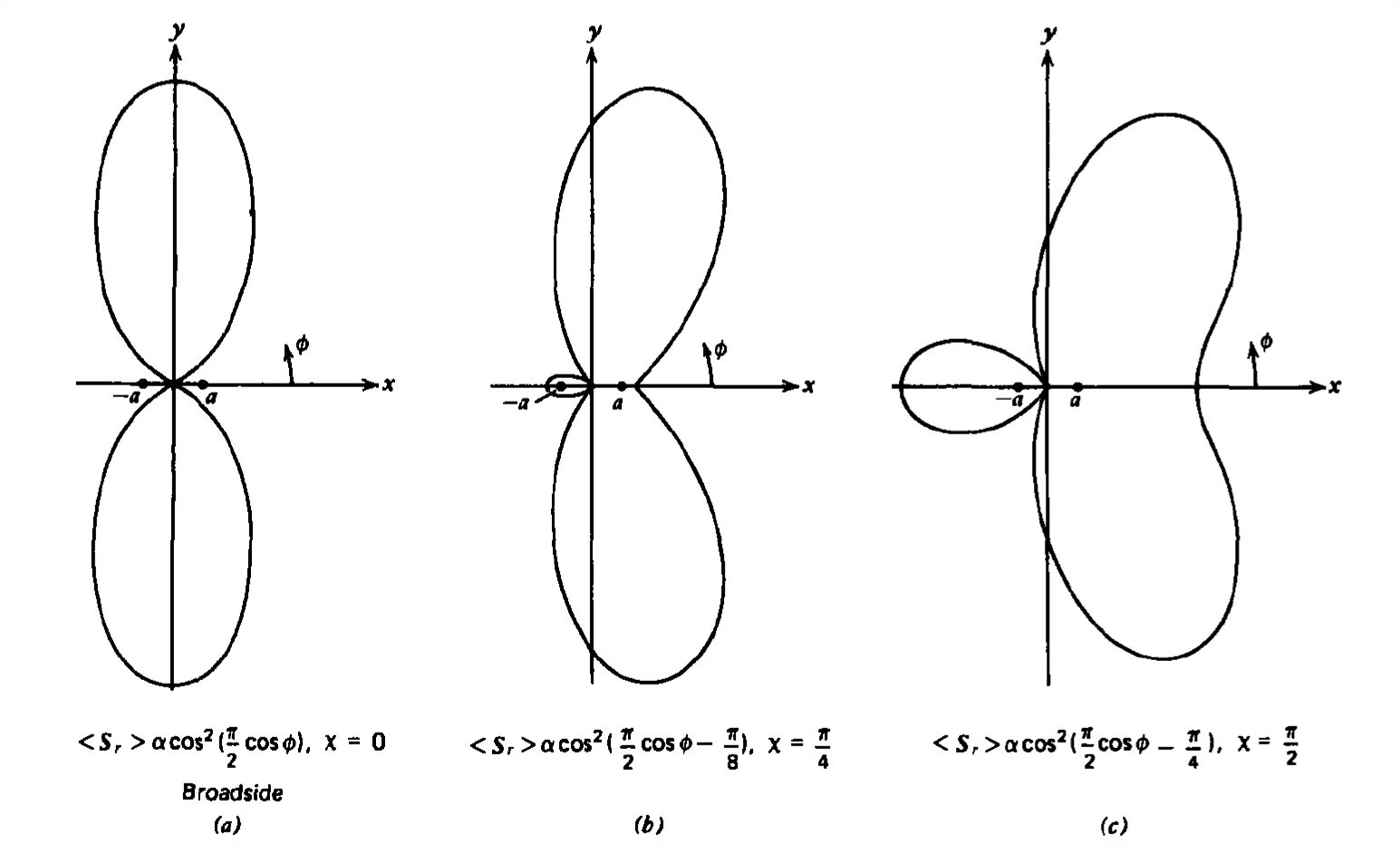
b) Matriz de fuego final

Sin embargo, si para el mismo espaciado de media longitud de onda las corrientes están desfasadas\(\left ( \mathcal{X}= \pi \right )\), los campos se suman a lo largo del\(x\) eje pero cancelan a lo largo del\(y\) eje. Aquí, aunque las longitudes de trayectoria a lo largo del\(y\) eje son las mismas para cada dipolo, debido a que las corrientes están desfasadas los campos cancelan. A lo largo del\(x\) eje la\(\pi\) fase extra debido a la diferencia de trayectoria de media longitud de onda simplemente se cancela por la diferencia de fase actual de\(\pi\) modo que los campos debidos a cada dipolo se suman. El patrón de radiación se llama fin de fuego porque la potencia es máxima en la dirección a lo largo de la matriz, como se muestra en la Figura 9-7e.

c) Fase corriente arbitraria

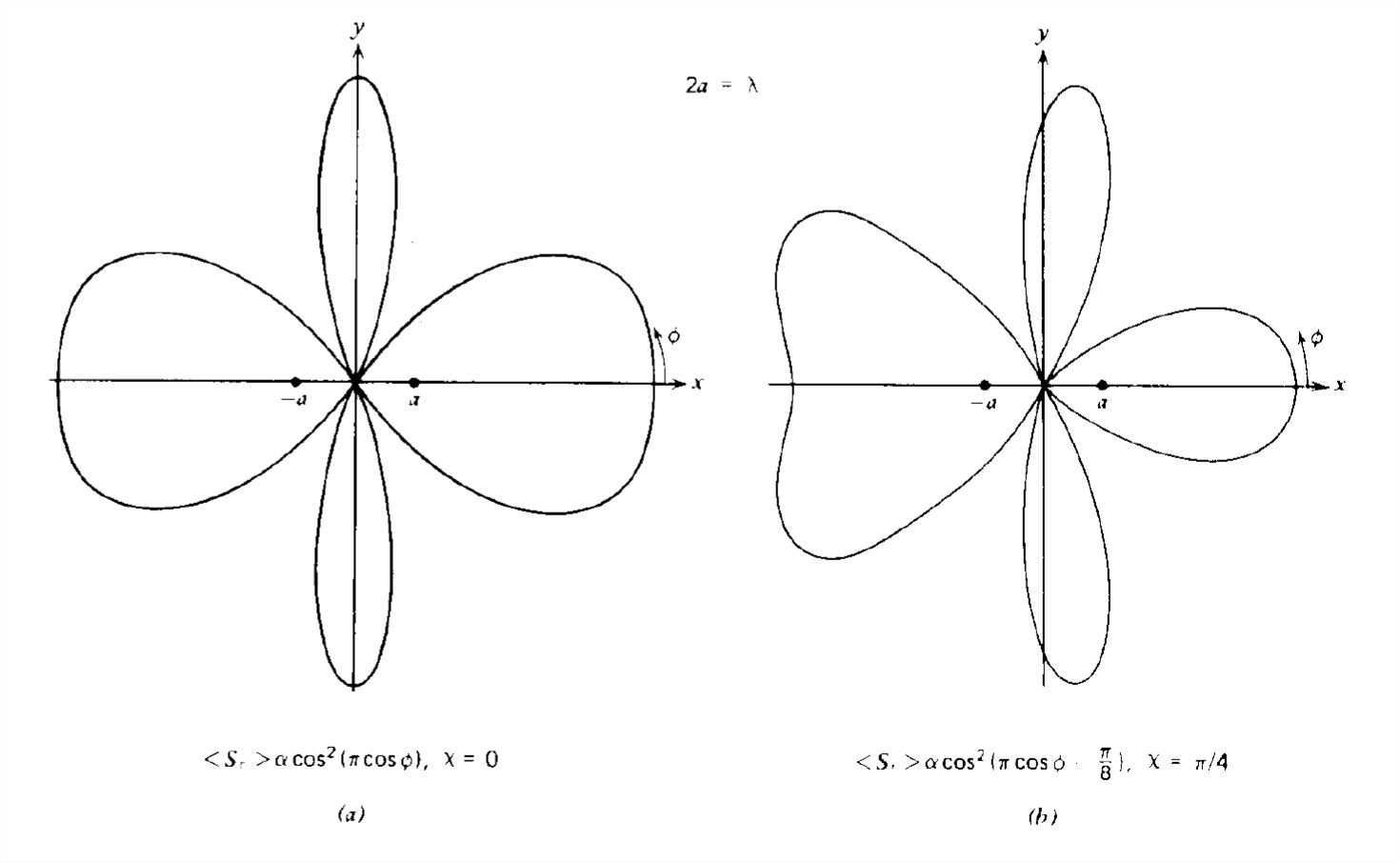
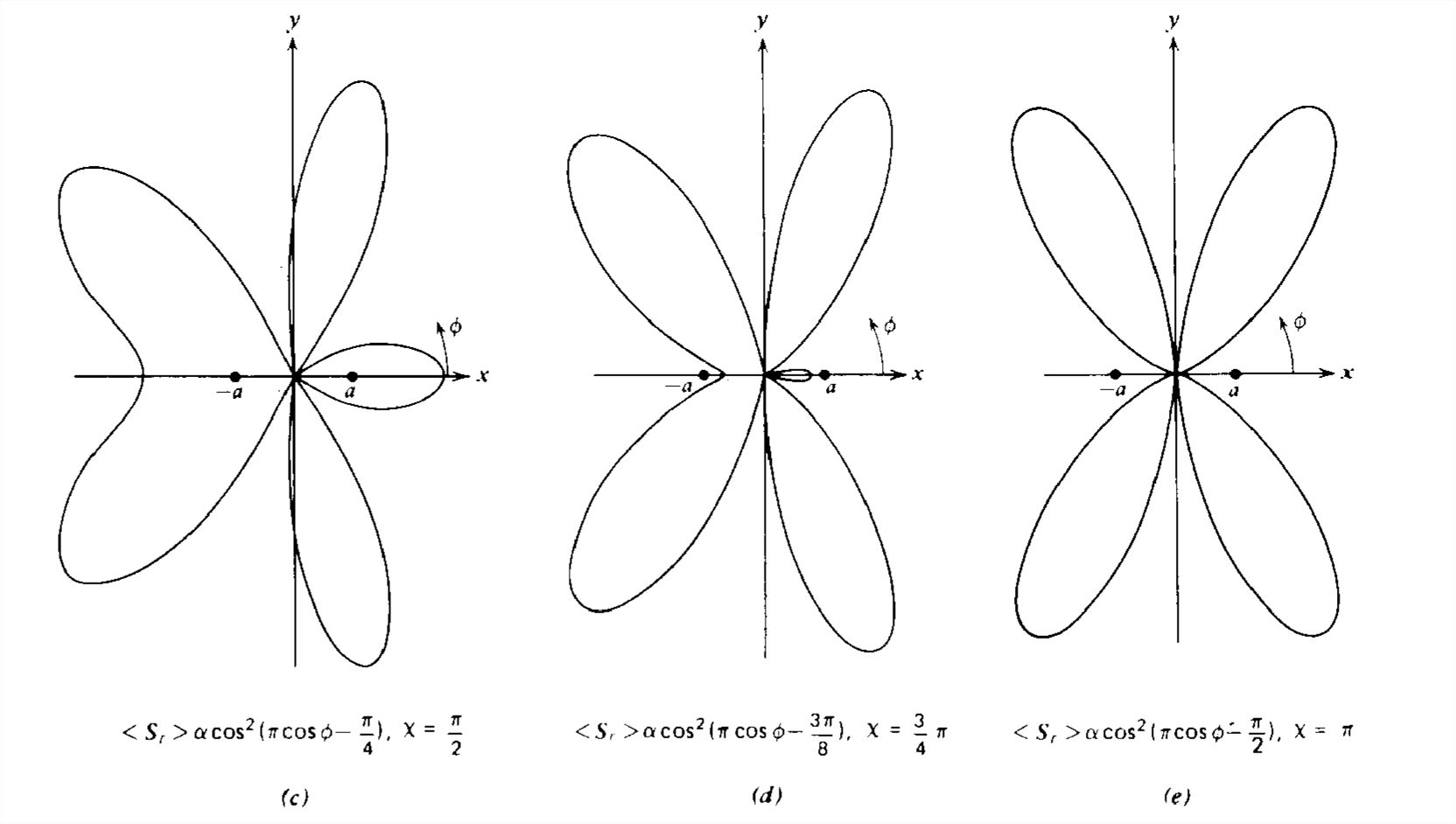
Para ángulos arbitrarios de fase de corriente y separaciones de dipolos, se puede obtener una gran variedad de patrones de radiación, como se ilustra por las secuencias de las Figuras 9-7 y 9-8. Aparecen más lóbulos de potencia a medida que aumenta el espaciamiento de los dipolos.

Una matriz de dipolos N

Si tenemos dipolos\((2N+ 1)\) igualmente espaciados, como se muestra en la Figura 9-9, la distancia del dipolo\(n\) th al punto de campo lejano es aproximadamente,

\[ \lim_{r\gg \left | na \right |}r_{n}\approx r-na\sin \theta \cos \phi  \nonumber \]

para que el factor de matriz de (4) generalice a

\[ AF=\sum_{-N}^{+N}\hat{I}_{n}dl_{n}e^{jkna\sin \theta \cos \phi } \nonumber \]

donde para la simetría asumimos que hay tantos dipolos a la izquierda (negativos\(n\)) como a la derecha (positivos\(n\)) del\(z\) eje, incluyendo uno en el origen\((n = 0)\). En el caso de que un dipolo no esté presente en una ubicación determinada, simplemente dejamos que su corriente sea cero. El factor de matriz se puede variar cambiando la magnitud o fase actual en los dipolos. Por simplicidad aquí, suponemos que todos los dipolos tienen la misma longitud\(dl\), la misma magnitud de corriente\(\hat{I}_{0}\), y difieren en fase de sus vecinos por un ángulo constante de\(\mathcal{X}_{0}\) manera que

\[ \hat{I}_{n}=I_{0}e^{-jn\mathcal{X}_{0}},\quad -N\leq N \nonumber \]

y (9) se convierte

\[ AF=I_{0}dl\sum_{-N}^{+N}e^{jn}\left ( ka\sin \theta \cos \phi -\mathcal{X}_{0} \right ) \nonumber \]

Figura 9-8 Con un espaciado de dipolo de longitud de onda completa\(\left ( 2a=\lambda  \right )\) hay cuatro lóbulos de alimentación principales.

Definir el parámetro

\[ \beta =e^{j\left ( ka\sin \theta \cos \phi -\mathcal{X}_{0} \right )} \nonumber \]

la serie geométrica en (11) se puede escribir como

\[ S=\sum_{-N}^{+N}\beta ^{n}=\beta ^{-N}+\beta ^{-N+1}+\cdots +\beta ^{-2}+\beta ^{-1}+1+\beta +\beta ^{2}+\cdots +\beta ^{N-1}+\beta ^{N} \nonumber \]

Si multiplicamos esta serie por\(\beta\) y restamos de (13), tenemos

\[S\left ( 1-\beta  \right )=\beta ^{-N}-\beta ^{N+1} \nonumber \]

lo que nos permite escribir la suma de la serie en forma cerrada como

\[ S=\frac{\beta ^{-N}-\beta ^{N+1}}{1-\beta }=\frac{\beta ^{-\left (N+1/2  \right )}-\beta ^{\left (N+1/2  \right )}}{\beta ^{-1/2}-\beta ^{-1/2}} =\frac{\sin \left [ \left ( N+\frac{1}{2}\right )\left ( ka\sin \theta \cos \phi -\mathcal{X}_{0} \right ) \right ]}{\sin \left [\frac{1}{2}\left ( ka\sin \theta \cos \phi -\mathcal{X}_{0} \right ) \right ]} \nonumber \]

En particular, volvemos a enfocarnos en la solución en el\(\theta =\pi /2\) plano para que el factor de matriz sea

\[ AF=I_{0}dl\frac{\sin \left [ \left ( N+\frac{1}{2} \right )\left ( ka\cos \phi -\mathcal{X}_{0} \right ) \right ]}{\sin \left [ \frac{1}{2}\left ( ka\cos \phi -\mathcal{X}_{0} \right ) \right ]} \nonumber \]

El patrón de radiación es proporcional al cuadrado del factor de matriz. Maxima ocurren donde

\[ ka\cos \phi -\mathcal{X}_{0} =2n\pi \quad n=0,1,2... \nonumber \]

El máximo principal es para\(n =0\) como se ilustra en la Figura 9-10 para diversos valores de\(ka\) y\(\mathcal{X}_{0}\). Cuanto mayor sea el número de dipolos\(N\), más estrecho será el máximo principal con lóbulos laterales de menor amplitud. Esto permite un haz altamente directivo en ángulo\(\phi \) controlado por el ángulo de fase de corriente incremental\(\mathcal{X}_{0}\), de modo que\(\cos \phi =\mathcal{X}_{0}/ka\), lo que permite la dirección electrónica del haz simplemente cambiando\(\mathcal{X}_{0}\).