Descripción de la matriz
Es importante que cada paso en la FFT de Winograd pueda describirse utilizando matrices. Expresando la convolución cíclica como una forma bilineal, se puede obtener una forma compacta de DFT de longitud de prima.
Si\(y\) es la convolución cíclica de\(h\) y\(x\), entonces se\(y\) puede expresar como
\[y=C\left [ Ax.\ast Bh \right ] \nonumber \]
donde, usando la convención de Matlab, .* representa multiplicación punto por punto. Cuándo\(A\),\(B\) y\(C\) se les permite ser complejos,\(A\) y\(B\) se ven como el operador DFT y\(C\), el DFT inverso. Cuando sólo se permiten números reales\(A\),,\(B\) y\(C\) serán rectangulares. Usando la propiedad de intercambio matricial, este formulario puede escribirse como
\[y=RB^{T}\left [ C^{T}Rh.\ast Ax \right ] \nonumber \]
donde\(R\) está la matriz de permutación que invierte el orden.
Cuando\(h\) es fijo, como lo es al considerar DFT de longitud prima, el término\(C^TRh\) puede ser precalculado y una matriz diagonal\(D\) formada por
\[D=diag{C^{T}Rh} \nonumber \]
Esto es ventajoso porque en general,\(C\) es más complicado que\(B\), por lo que la capacidad de “ocultar”\(C\) guarda cómputos. Ahoray=RBTDAxy=RBTDAx“role="presentación” style="position:relative;” tabindex="0">
\[y=RB^{T}DAx\; \; or\; \; y=RA^{T}DAx \nonumber \]
ya que\(A\) y\(B\) pueden ser lo mismo; implementan una reducción polinómica. El formulario también se\(y=R^{T}DAxT\) puede utilizar para las DFT de longitud principal, solo es necesario permutar las entradas de\(x\) y asegurar que el\(DC\) término se compute correctamente. El cálculo del\(DC\) término es sencillo, pues el residuo de un módulo polinómico\(a-1\) es siempre la suma de los coeficientes. Después de agregar el\(x_0\) término de la secuencia de entrada original, al\(s-1\) residuo, se obtiene el\(DC\) término. Ahora
\[DFT\left \{ x \right \}=RA^{T}DAx \nonumber \]
Johnson observa que permutando los elementos en la diagonal de\(D\), la salida puede permutarse, de modo que la\(R\) matriz se pueda ocultar en\(D\), y
DFT{x}=ATDAxDFT{x}=ATDAx“role="presentación” style="position:relative;” tabindex="0"> \[DFT\left \{ x \right \}=A^{T}DAx \nonumber \]
A partir del conocimiento de esta forma, una vez que\(A\) se encuentra, se\(D\) puede encontrar numéricamente.
Programación del Procedimiento de Diseño
Debido a que cada uno de los pasos anteriores puede describirse mediante matrices, el desarrollo de un FFT de longitud primo se hace conveniente con el uso de un lenguaje de programación orientado a matriz como Matlab. Después de especificar las matrices apropiadas que describen el algoritmo FFT deseado, generar código implica compilar las matrices en el código deseado para su ejecución.
Cada matriz es una sección de una etapa del gráfico de flujo que corresponde al programa DFT. Las cuatro etapas son:
- Etapa de Permutación: Permuta la secuencia de entrada y salida.
- Etapa de reducción: Reduce la convolución cíclica a productos polinómicos más pequeños.
- Etapa Polinomial del Producto: Realiza las multiplicaciones polinomiales.
- Etapa de Multiplicación: Implementa la multiplicación punto por punto en la forma bilineal.
Cada una de las etapas se puede ver claramente en las gráficas de flujo para las DFT. La Fig. 6.5.1 muestra el gráfico de flujo para un algoritmo\(17\) DFT de longitud que fue dibujado automáticamente por el programa.
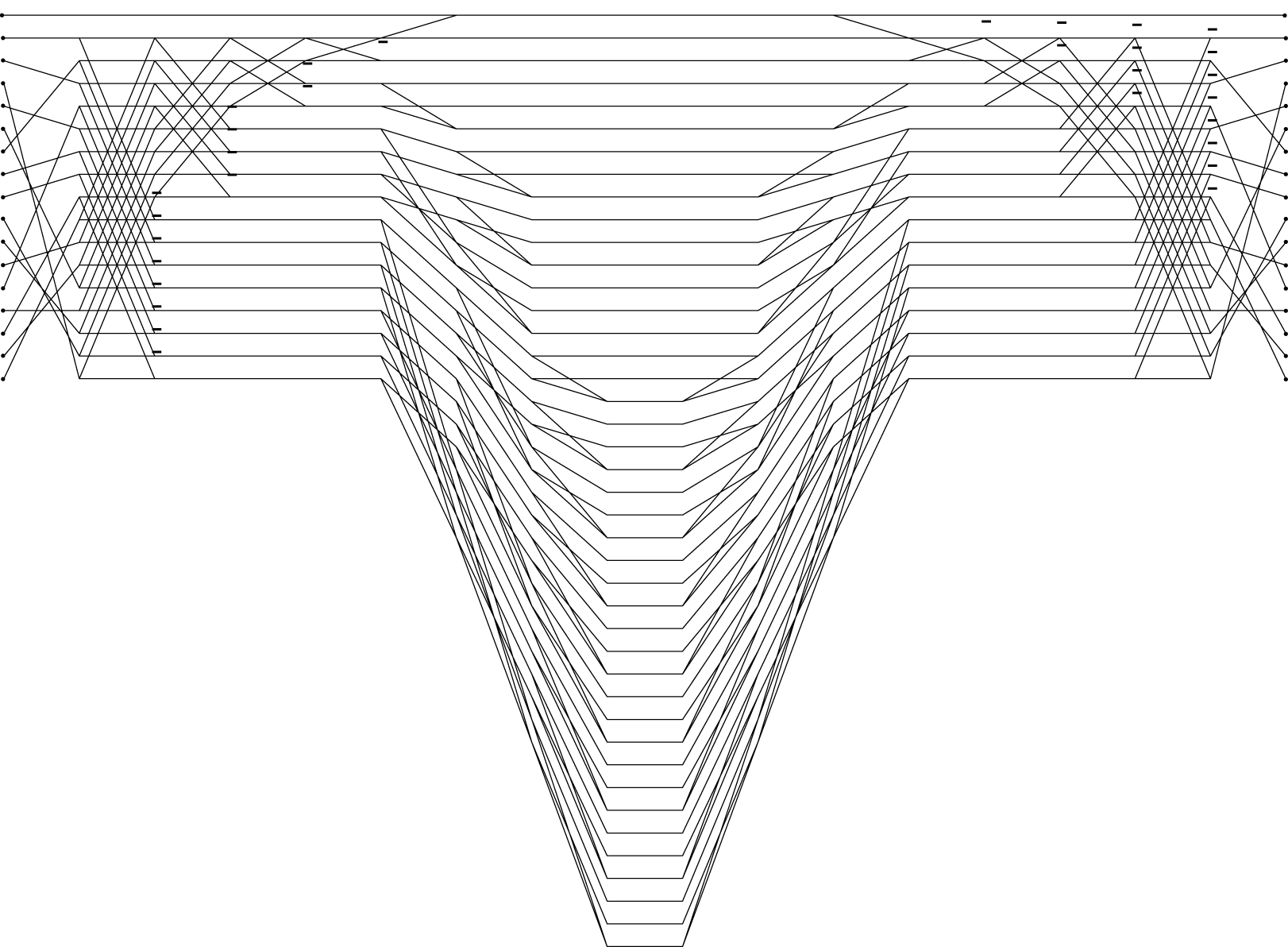
Fig. 6.5.1 Flujograma de longitud 17 DFT
Los programas que logran este proceso están escritos en Matlab y C. Aquellos que computan las matrices apropiadas están escritos en Matlab. Estas matrices se almacenan luego como dos archivos ASCII, con las dimensiones en uno y los elementos de la matriz en el segundo. Un programa C luego lee las moscas y las compila para producir el programa FFT final en C.
La etapa de reducción
La reducción de un\(N^{th}\) grado polinomio\(X(s)\), módulo los factores polinómicos ciclotómicos de (\(s^N-1\)) solo requiere adiciones para muchos\(N\), sin embargo, el número real de adiciones depende de la forma en que proceda la reducción. La reducción se realiza de manera más eficiente en etapas. Por ejemplo,
\[If\; \; N=4\; \; and\; \; ((X(s)))_{s-1},\; \; ((X(s)))_{s+1}\; \; and\; \; ((X(s)))_{s^{2}+1}, \nonumber \]
donde el paréntesis doble denota módulo de reducción polinómica(s-1)(s-1)“role="presentación” style="position:relative;” tabindex="0">
\[(s-1),\; \; (s+1),\; \; and\; \; (s^{2}+1) \nonumber \]
luego en el primer paso
((X(s)))s2-1((X(s)))s2-1“role="presentación” style="position:relative;” tabindex="0"> \[((X(s)))_{s^{2}-1}\; \; and\; \; ((X(s)))_{s^{2}+1} \nonumber \]
deben ser computados.
En el segundo paso,
((Xs)))s-1((Xs)))s-1“role="presentación” style="position:relative;” tabindex="0"> \[((X(s)))_{s-1}\; \; and\; \; ((X(s)))_{s+1} \nonumber \]
se puede encontrar reduciendo((X(s)))s2-1((X(s)))s2-1“role="presentación” style="position:relative;” tabindex="0">
\[((X(s)))_{s^{2}-1} \nonumber \]
Este proceso se describe en el diagrama de la Fig. 6.5.2 a continuación.
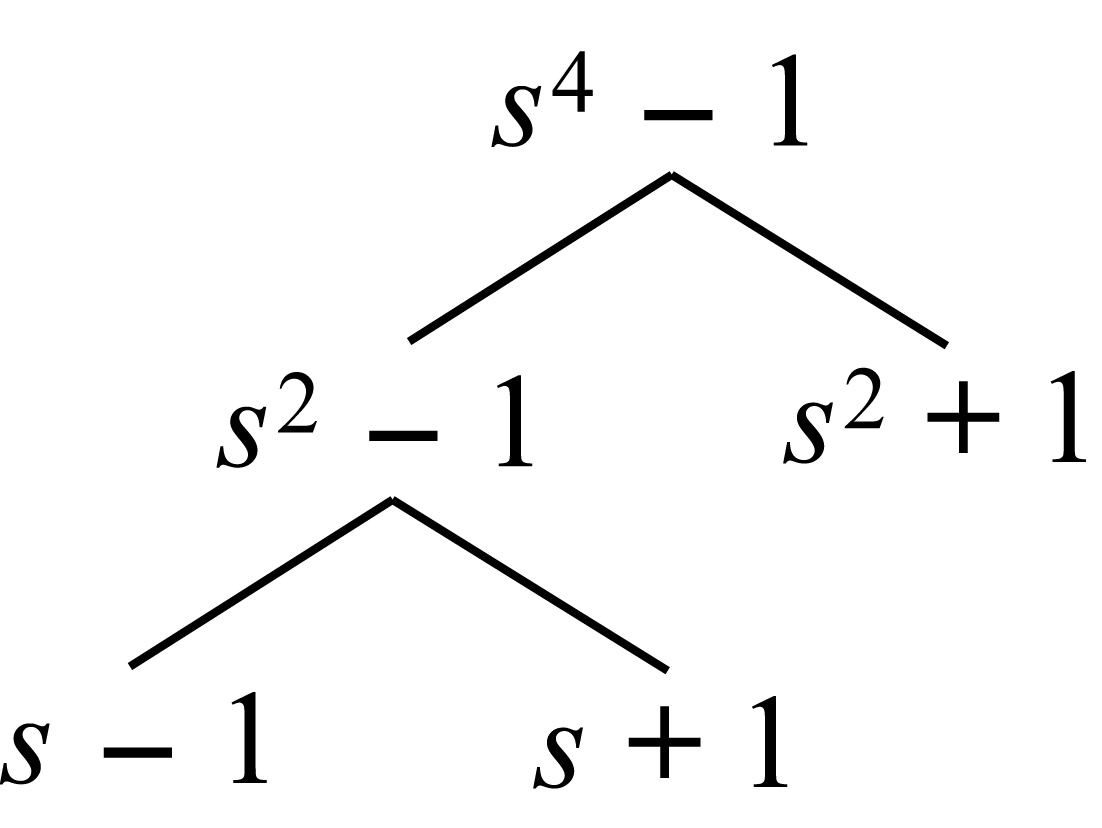
Fig. 6.5.2 Factorización de s 4 -1 en etapas
Cuando\(N\) es par, la primera factorización apropiada es
(SN/2-1)(sN/2+1)(SN/2-1)(sN/2+1)“role="presentación” style="position:relative;” tabindex="0"> \[(S^{N/2}-1)(S^{N/2}+1) \nonumber \]
Sin embargo, la siguiente factorización apropiada es frecuentemente menos obvia. Se ha encontrado que el siguiente procedimiento genera una factorización en etapas que coincide con la factorización que minimiza el número acumulado de adiciones incurridas por los escalones. Los factores primos de\(N\) son la base de este procedimiento y su importancia queda clara a partir de la útil ecuación bien conocida:
\[s^{N}-1=\prod _{n\mid N}C_{n}(s) \nonumber \]
donde\(C_n(s)\) está el polinomio\(n^{th}\) ciclotómico.
Primero introducimos las siguientes dos funciones definidas sobre los enteros positivos,
\[\psi (N)=the\; smallest\; prime\; factor\; of\; N\; for\; N>1\; and\; \psi (1)=1 \nonumber \]
Supongamos que\(P(s)\) es igual a cualquiera de (\(s^N-1\)) o a un polinomio no ciclotómico intermedio que aparece en el proceso de factorización, por ejemplo, (\(a^2-1\)), arriba. Escribir\(P(s)\) en términos de sus factores ciclotómicos,
(sN-1)(sN-1)“role="presentación” style="position:relative;” tabindex="0"> \[P(s)=C_{k_{1}}(s)C_{k_{2}}(s)...C_{k_{L}}(s) \nonumber \]
definir los dos conjuntos,\(G\) y\(G\), por
\[G=\left \{ k_{1},...,k_{L} \right \}\; and\; G=\left \{ k/gcd(G):k\epsilon G \right \} \nonumber \]
y definir los dos enteros,\(t\) y\(T\), por
\[t=min\left \{ \psi (k):k\: \epsilon\: G,\: k>1 \right \}\; \; and\; \; T=max\: nu(k,t):k\: \epsilon \: G \nonumber \]
Luego formar dos nuevos conjuntos,
\[A=\left \{ k\: \epsilon \: G:T\mid k \right \}\; \; and\; \; B=\left \{ k\: \epsilon \: G:T\mid k \right \} \nonumber \]
La factorización de\(P(s)\),
\[P(s)=\left ( \prod _{k\: \epsilon \: A} C_{k}(s)\right )\left ( \prod _{k\: \epsilon \: B} C_{k}(s)\right ) \nonumber \]
se ha encontrado útil en el procedimiento de factorización (\(s^N-1\)). Esto se ilustra mejor con un ejemplo.
Ejemplo
\(N=36\)
Paso 1:
Let
\[P(s)=s^{36}-1 \nonumber \]
Desde
\[P=C_{1}C_{2}C_{3}C_{4}C_{6}C_{9}C_{12}C_{18}C_{36} \nonumber \]
\[G=G=\left \{ 1,2,3,4,6,9,12,18,36 \right \} \nonumber \]
\[t=min\; \left \{ 2,3 \right \}=2 \nonumber \]
\[A=\left \{ k\: \epsilon \: G:4\mid k \right \}=\left \{ 1,2,3,6,9,18 \right \} \nonumber \]
\[B=\left \{ k\: \epsilon \: G:4\mid k \right \}=\left \{ 4,12,36 \right \} \nonumber \]
De ahí que la factorización de\(s^{36}-1\) dos polinomios intermedios sea la esperada,
\[\prod _{k\: \epsilon \: A} C_{k}(s)=s^{18}-1,\; \; \prod _{k\: \epsilon \: B} C_{k}(s)=s^{18}+1 \nonumber \]
Si un polinomio\(36^{th}\) grado,\(X(s)\), está representado por un vector de coeficientes,
\[X=(x_{35},...x_{0})'\; then\; ((X(s)))_{s^{18}-1}\; represented\; by\; X'\; and\; ((X(s)))_{s^{18}+1}\; represented\; by\; X'' \nonumber \]
se da por prueba que implica\(36\) adiciones.
Paso 2:
Este procedimiento se repite conP(s)=s18-1P(s)=s18-1“role="presentación” style="position:relative;” tabindex="0">
\[P(s)=s^{18}-1 \; and\; P(s)=s^{18}+1 \nonumber \]
Simplemente lo mostraremos para el posterior. LetP(s)=s18+1P(s)=s18+1“role="presentación” style="position:relative;” tabindex="0">
\[P(s)=s^{18}+1 \nonumber \]
Desde
\[P=C_{4}C_{12}C_{36} \nonumber \]
\[G=\left \{ 4,12,36 \right \}\; and\; G'=\left \{ 1,3,9 \right \} \nonumber \]
\[t=min\: 3=3 \nonumber \]
\[T=max\: \nu (k,3):k\: \epsilon \: G=max\: 1,3,9=9 \nonumber \]
\[A=\left \{ k\: \epsilon \: G:9\mid k \right \}=\left \{ 4,12\right \} \nonumber \]
\[B=\left \{ k\: \epsilon \: G:9\mid k \right \}=\left \{ 36\right \} \nonumber \]
Esto produce los dos polinomios intermedios
\[s^{6}+1\; \; and\; \; s^{12}-s^{6}+1 \nonumber \]
En la notación utilizada anteriormente,
\[\begin{bmatrix} X' & X'' \end{bmatrix}=\begin{bmatrix} I_{6} & -I_{6} & I_{6}\\ I_{6} & I_{6} & \\ -I_{6} & & I_{6} \end{bmatrix}X \nonumber \]
que conllevan\(24\) adiciones. Continuar con este proceso da como resultado una factorización en pasos.
Para ver el número de adiciones que este esquema utiliza para los números de la forma\(N=P-1\) (que es relevante para los algoritmos FFT de longitud de primos).
La etapa del producto polinomial
El algoritmo de convolución iterada se puede utilizar para construir un algoritmo de convolución lineal\(N\) puntual a partir de algoritmos de convolución lineal más cortos. Supongamos que la convolución lineal\(y\), de los n vectores puntuales\(x\) y\(h\) (\(h\)conocida) es descrita por
\[y=E_{n}^{T}DE_{n}x \nonumber \]
donde\(E_n\) es una matriz de “expansión” cuyos elementos son\(\pm 1\)'s y\(0\)'s y\(D\) es una matriz diagonal apropiada. Porque las únicas multiplicaciones en esta expresión son por los elementos de\(D\), el número de multiplicaciones requeridas\(M(n)\),, es igual al número de filas de\(E_n\). El número de adiciones se denota por\(M(n)\).
Dada una matriz\(E_{n1}\) y una matriz\(E_{n2}\), el algoritmo iterado da un método para combinar\(E_{n1}\) y\(E_{n2}\) construir una matriz de expansión válida,\(E_{n}\), para
\[N\leq n_{1}n_{2} \nonumber \]
Específicamente,
\[E_{n_{1},n_{2}}=(I_{m(n_{2})}\otimes E_{n_{1}})(E_{n_{2}}\times I_{n_{1}}) \nonumber \]
El producto\(n_1n_2\) puede ser mayor que\(N\), porque los ceros pueden ser (conceptualmente) anexados a\(x\). El recuento de operaciones asociado con\(E_{n1}E_{n2}\) es
\[A(n_{1},n_{2})=n!A(n_{2})+A(n_{1})M(n_{2}) \nonumber \]
\[M(n_{1},n_{2})=M(n_{1})M(n_{2}) \nonumber \]
Aunque ambas son matrices de expansión válidas,
\[E_{n_{1},n_{2}}\neq E_{n_{2},n_{1}}\; \; and\; \; A_{n_{1},n_{2}}\neq A_{n_{2},n_{1}} \nonumber \]
PorqueMn1,n2≠Mn2,n1Mn1,n2≠Mn2,n1“role="presentación” style="position:relative;” tabindex="0">
\[M_{n_{1},n_{2}}\neq M_{n_{2},n_{1}} \nonumber \]
es deseable elegir un orden de factores para minimizar las adiciones en las que incurre la matriz de expansión.
Múltiples factores
Tenga en cuenta que una matriz de expansión válida,\(E_{n}\), se puede construir a partir de\(E_{n_1,n_2}\) y\(E_{n3}\), para
N≤n1n2n3N≤n1n2n3“role="presentación” style="position:relative;” tabindex="0"> \[N\leq n_{1}n_{2}n_{3} \nonumber \]
En general, se puede utilizar cualquier número de factores para crear matrices de expansión más grandes. El recuento de operaciones asociado con\(E_{n_1,n_2,n_3}\) es
\[A(n_{1},n_{2},n_{3})=n_{1}n_{2}A(n_{3})+n_{1}A(n_{2})M(n_{3})+A(n_{1})M(n_{2})M(n_{3}) \nonumber \]
\[M(n_{1},n_{2},n_{3})=M(n_{1})M(n_{2})M(n_{3}) \nonumber \]
Estas ecuaciones se generalizan de la manera predicha cuando se consideran más factores. Debido a que el orden de los factores es relevante en la ecuación para\(A(\cdot )\) pero no para\(M(\cdot )\), nuevamente es deseable ordenar los factores para minimizar el número de adiciones. Al explotar la siguiente propiedad de las expresiones para\(A(\cdot )\) y\(M(\cdot )\), se puede encontrar el orden óptimo.
Reserva de Pedido Óptimo
Supongamos
\( A(n_1,n_2,n_3) \le \text{min} \{A(n_{k_1},n_{k_2},n_{k_3}) \: k_1,k_2,k_3 \in \{1,2,3\} \text{ and distinct} \} \), luego
| 1. |
\(A(n_1,n_2) \le A(n_2,n_1)\) |
| 2. |
\(A(n_2,n_3) \le A(n_3,n_2)\) |
| 3. |
\(A(n_1,n_3) \le A(n_3,n_1)\) |
La generalización de esta propiedad a más de dos hechos revelas de que\( \{n_1, \ldots , n_{L-i} \} \) se conserva un ordenamiento óptimo en un ordenamiento óptimo de\( \{n_1, \ldots , n_{L} \} \). Por lo tanto, si\( (n_1, \ldots , n_{L-i}) \) es un odering óptimo de\( \{n_1, \ldots , n_{L} \} \), entonces\( (n_k,n_{k+1}) \) es un orden óptimo de\( \{ n_k,n_{k+1} \} \) y consecuentemente
\[ \dfrac{A(n_k)}{M(n_k)-n_k} \le \dfrac{A(n_{k+1})}{M(n_{k+1})-n_{k+1}} \nonumber \]
para todos\(k=1,2,\ldots,L-1\).
Esto inmediatamente sugiere que un orden óptimo de\( \{n_1, \ldots , n_L \} \), para minimizar el número de adiciones incurridos por\( E_{n_1, \ldots , n_L}\) simplemente implica calcular las proporciones apropiadas.
Discusión y Conclusión
Hemos diseñado FFT de longitud principal hasta la longitud\(53\) que son tan buenos como los diseños anteriores que solo fueron hasta\(19\). En el Cuadro 1 se dan los recuentos de operación para los módulos nuevos y previamente diseñados, asumiendo entradas complejas.
Es interesante señalar que los conteos de operación dependen de la factoriabilidad de\(P−1\). Los primos\(11\),\(23\), y\(47\) son todos de la forma,\(1+2P_1\) lo que dificulta el diseño de FFT eficientes para estas longitudes.
Otras desviaciones del enfoque original de Winograd que las que hemos hecho podrían resultar útiles para longitudes más largas. Se investigó, por ejemplo, el uso de factores de twiddle en puntos apropiados en la etapa de descomposición; estos a veces pueden ser utilizados para dividir la convolución cíclica en convoluciones más pequeñas. Su uso significa, sin embargo, que las multiplicaciones 'centro* ya no serían por números puramente reales o imaginarios.
| N |
Mut |
Agrega |
| 7 |
16 |
72 |
| 11 |
40 |
168 |
| 13 |
40 |
188 |
| 17 |
82 |
274 |
| 19 |
88 |
360 |
| 23 |
174 |
672 |
| 29 |
190 |
766 |
| 31 |
160 |
984 |
| 37 |
220 |
920 |
| 41 |
282 |
1140 |
| 43 |
304 |
1416 |
| 47 |
640 |
2088 |
| 53 |
556 |
2038 |
Recuentos de operación para DFT de longitud principal
El enfoque al escribir un programa que escribe otro programa es valioso por varias razones. Programar el proceso de diseño para el diseño de FFT de longitud principal tiene las ventajas de ser práctico, libre de errores y flexible. La flexibilidad es importante porque permite la modificación y experimentación con diferentes ideas algorítmicas. Sobre todo, ha permitido diseñar confiablemente los DFT más largos.
Más detalles sobre la generación de programas para FFT de longitud prime se pueden encontrar en el Informe Técnico de 1993.




