3.7: Dispersión de luz por una hendidura
- Page ID
- 82261
Uno de los éxitos más espectaculares para el análisis fasorial surge en el estudio de la difracción de luz por una hendidura estrecha. El experimento consiste en hacer brillar luz láser a través de una hendidura en una lámina opaca y observar el patrón de luz que cae sobre una pantalla distante. Cuando la hendidura es muy estrecha en comparación con la longitud de onda de la luz, entonces la luz que cae sobre la pantalla es casi uniforme en intensidad. Sin embargo, cuando el ancho de la hendidura es comparable a la longitud de onda de la luz, el patrón de luz que cae sobre la pantalla es festoneado en intensidad, mostrando bandas alternas de luz y oscuridad. El experimento, y los resultados observados, se ilustran en la Figura.
Figura\(\PageIndex{1}\): Difracción de luz por una hendidura
¿Por qué este experimento debería producir este resultado? El análisis fasorial ilumina la pregunta y produce una elegante descripción matemática de un experimento óptico profundamente importante.
Principio de Huygens
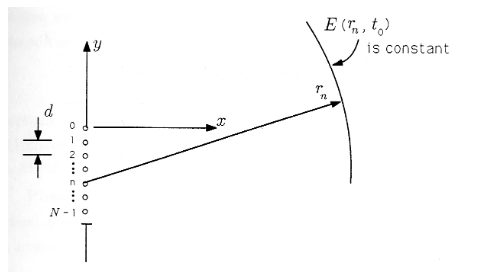
Supondremos, como lo hizo Christiaan Huygens, que la luz incidente en la hendidura establece un campo de luz en la hendidura que puede ser modelado por fuentes\(N\) discretas, cada una de las cuales irradia una “onda esférica de luz”. Este modelo se ilustra en la Figura. La distancia entre fuentes es\(d\), y\(Nd=L\) es el ancho de la hendidura. Cada fuente está indexada por\(n\), y\(n\) se ejecuta de 0 a\(N−1\). La fuente 0 se encuentra en el origen de nuestro sistema de coordenadas.
La onda esférica irradiada por la\(n^{\mathrm{th}}\) fuente se describe mediante la ecuación
\[E(r_n,t)=\mathrm{Re}\{\frac A N e^{j[ωt−(2π/λ)r_n]}\} \nonumber \]
La función\(E(r_n,t)\) describe el “campo eléctrico” en el tiempo\(t\) y la\(r_n\) distancia de la\(n^\mathrm{th}\) fuente. El campo es constante siempre y cuando la variable\(ωt−(2π/λ)r_n\) sea constante. Por lo tanto, si congelamos el tiempo en\(t=t_0\), el campo será constante en una esfera de radio\(r_n\). Esto se ilustra en la Figura.
Fijar\(r_n\)\(E(r_n,t)\) y mostrar que\(E(r_n,t)\) varía cosinusoidalmente con el tiempo\(t\). Esbozar la función e interpretarla. ¿Cuál es su periodo?
Fijar\(t\)\(E(r_n,t)\) y mostrar que\(E(r_n,t)\) varía cosinusoidalmente con el radio\(r_n\). Esbozar la función e interpretarla. Llame al “período en\(r_n\)" la “longitud de onda”. Demuestre que la longitud de onda es\(λ\).
La “cresta de la ola\(E(r_n,t)\)" se produce cuando\(ωt−(2π/λ)r_n=0\). Demuestre que la cresta se mueve a través del espacio a velocidad\(v=ωλ/2π\).
Geometría
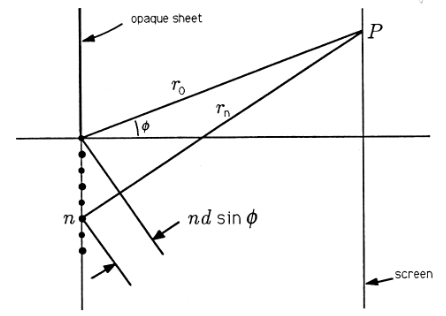
Si ahora elegimos un punto\(P\) en una pantalla distante, ese punto estará a distancia\(r_0\) de la fuente 0,... ,\(r_n\) de fuente\(n\),..., y así sucesivamente. Si aislamos las fuentes 0 y\(n\), entonces tenemos la imagen geométrica de la Figura. El ángulo\(φ\) es el ángulo que\(P\) hace el punto con el eje horizontal. El teorema de Pitágoras dice que la conexión entre distancias\(r_0\) y\(r_n\) es
\[(r_n−nd\sinφ)^2+(nd\cosφ)^2=r^2_0 \nonumber \]
Vamos a probar la solución
\[r_n=r_0+nd\sinφ \nonumber \]
Esta solución produce la identidad aproximada
\[r^2_0+(nd\cosφ)^2≅r^2_0 \nonumber \]
\[r^2_0+(nd\cosφ)^2≅r^2_0 \nonumber \]
\[1+(\frac {nd} {r_0} \cosφ)^2≅1 \nonumber \]
Esto va a estar cerca para\(\frac {nd} {r_0} <<1\). Supondremos que el ancho de la hendidura\(L\) es pequeño en comparación con la distancia a cualquier punto de la pantalla.
Entonces\(\frac {Nd} {r_0} = \frac {L} {r_0} << 1\), en cuyo caso la solución aproximada para\(r_n\) es válida para todos\(n\). Esto significa que, para cualquier punto de\(P\) la pantalla distante, la luz aportada por la\(n^{th}\) fuente es aproximadamente
\[E_n(φ,t)=\mathrm{Re}\{\frac A N e^{j[ωt−(2π/λ)(r_0+nd\sinφ)]}\}=\mathrm{Re}\{\frac A N e^{−j(2π/λ)r_0}e^{−j(2π/λ)nd\sinφ}e^{jωt}\} \nonumber \]
La representación fasora para esta función es solo
\[E_n(φ)=\frac A N e^{−j(2π/λ)r_0} e^{−j(2π/λ)nd\sinφ} \nonumber \]
Tenga en cuenta que\(E_0(φ)\), el fasor asociado a la 0 th fuente, es\(\frac A N e^{−j(2π/λ)r_0}\). Por lo tanto, podemos escribir la representación fasorial para que la luz aportada por la\(n^{th}\) fuente sea
\[E_n(φ)=E_0(φ)e^{−j(2π/λ)nd\sinφ} \nonumber \]
Este resultado es muy importante porque muestra que la luz que llega al punto\(P\) de diferentes fuentes está “desfasada” en una cantidad que depende de la relación\(\frac {nd\sinφ} λ\)
Fasores e Interferencia
La representación de fasores para el campo observado en el punto\(P\) de la pantalla es la suma de los fasores aportados por cada fuente:
\[E(φ)=∑_{n=0}^{N−1} E_n(φ)=E_0(φ)∑_{n=0}^{N−1}e^{−j(2π/λ)nd\sinφ} \nonumber \]
Esto es una suma de la forma
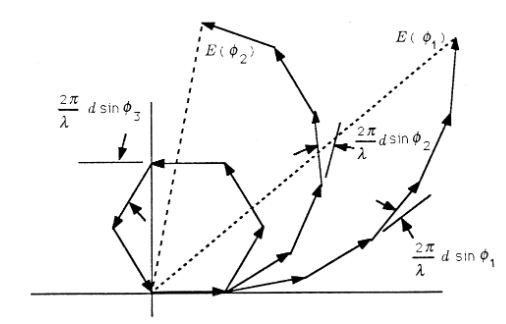
\[E(φ)=E_0(φ)∑_{n=0}^{N−1}e^{jnθ} \nonumber \]
donde\(θ\) está el ángulo\((2π/λ)d\sinφ\). Esta suma se ilustra en la Figura para varios valores representativos de\(θ\). Tenga en cuenta que para pequeños\(θ\), es decir\(φ\), pequeños, la suma tiene gran magnitud, mientras que para\(θ\) en el orden de\(2π/N\), la suma es pequeña. Esta sencilla interpretación geométrica muestra que para algunos valores de\(φ\), correspondientes a algunos puntos\(P\) de la pantalla, habrá interferencia constructiva entre los fasores, mientras que para otros valores de\(φ\) habrá interferencia destructiva. La interferencia constructiva produce luz brillante y la interferencia destructiva produce oscuridad.
La geometría de la Figura es iluminadora. Sin embargo, ya sabemos por nuestro estudio de números complejos y sumas geométricas que la suma fasorial de la Ecuación puede escribirse como
\[E(φ)=E_0(φ)\frac {1−e^{−j(2π/λ)Nd\sinφ}} {1−e^{−j(2π/λ)d\sinφ}} \nonumber \]
Este resultado puede ser manipulado para producir la forma
\[E(φ)=\frac A N e^{−j(2π/λ)r_0} e^{−j(π/λ)(N−1)d\sinφ}\frac {\sin(Nπ\frac d λ \sinφ)} {\sin(π\frac d λ \sinφ)} \nonumber \]
La magnitud es la intensidad de la luz en ángulo\(φ\) desde la horizontal:
\[|E(φ)|=|\frac A N \frac {\sin(Nπ\frac d λ \sinφ)} {\sin(π\frac d λ \sinφ)}| \nonumber \]
Derivar\(\frac A N e^{−j(2π/λ)r_0} e^{−j(π/λ)(N−1)d\sinφ}\frac {\sin(Nπ\frac d λ \sinφ)} {\sin(π\frac d λ \sinφ)}\) de\(E_0(φ)\frac {1−e^{−j(2π/λ)Nd\sinφ}} {1−e^{−j(2π/λ)d\sinφ}}\).
Forma limitante
El modelo de Huygens es exacto cuando d se contrae a 0 y N aumenta al infinito de tal manera que Nd→L, el ancho de la hendidura. Entonces
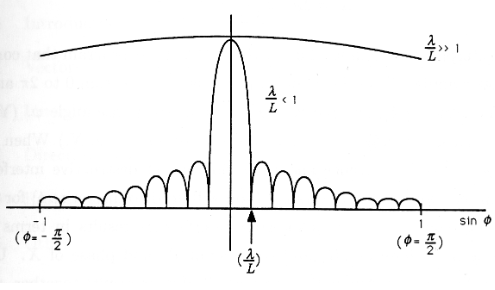
\[|E(φ)|→|\frac {A\sin(\frac {πL} λ \sinφ)} {\frac {πL} λ \sinφ}| \nonumber \]
Esta función se grafica en laFigura para dos valores\(\frac L λ\) del ancho de la hendidura medidos en longitudes de onda. Cuando\(\frac L λ<<1\) (es decir,\(/frac λ L >>1\)), entonces la luz se distribuye uniformemente en la pantalla. Sin embargo, cuando\(\frac L λ>1(\frac λ L<1)\), entonces la función tiene muchos ceros para\(\frac| \sin φ|<1\), como se ilustra en la figura. Estos ceros corresponden a manchas oscuras en la pantalla donde los campos irradiados desde la infinidad de puntos dentro de la hendidura interfieren destructivamente.
Derivar\(|\frac {A\sin(\frac {πL} λ \sinφ)} {\frac {πL} λ \sinφ}|\) de\(|\frac A N \frac {\sin(Nπ\frac d λ \sinφ)} {\sin(π\frac d λ \sinφ)}|\)
(MATLAB) Trazar la aproximación discreta\
\(∣\frac {\frac A N \sin(Nπ\frac d λ \sinφ)} {\sin(π\frac d λ \sinφ)}∣\)
versus\(\sin φ\) para\(\frac L λ=\frac {Nd} λ=10\) y N=2,4,8,16,32. Comparar con la forma continua y limitante
\(∣\frac {A\sin(π\frac L λ \sinφ)} {π\frac L λ \sinφ}∣\)


