4.7: Matrices

La matriz de palabras data por lo menos del siglo XIII, cuando se utilizó para describir la bandeja rectangular de cobre, o matriz, que sostenía letras plomo individuales que se empaquetaban en la matriz para formar una página de texto compuesto. Cada letra en la matriz, llámalo\(a_{ij}\), ocupaba una posición única (ij) en la matriz. En el lenguaje matemático moderno, una matriz es una colección de números dispuestos en una matriz bidimensional (un rectángulo). Indicamos una matriz con mayúscula en negrilla y los elementos constitutivos con subíndices dobles para la fila y columna:

Figura\(\PageIndex{1}\): Matriz. (Copyright; autor vía fuente)

En esta ecuación\(A\) hay una\(mxn\) matriz, es decir, que\(A\) tiene filas\(m\) horizontales y columnas\(n\) verticales. Como extensión de la notación utilizada anteriormente, escribimos\(A∈R^{mxn}\) para mostrar que A es una matriz de tamaño mxn con\(a_{ij}∈R\). ^{El elemento escalar\(a_{ij}\) se encuentra en la matriz en la fila i y la j ésima columna.} Por ejemplo, un ₂₃ se ubica en la segunda fila y la tercera columna como se ilustra en la Figura.

La diagonal principal de cualquier matriz consiste en los elementos a _ii. (Los dos subíndices son iguales.) La diagonal principal corre hacia el sureste desde la esquina superior izquierda de la matriz, pero no termina en la esquina inferior derecha a menos que la matriz sea cuadrada (\(∈R^{m×m}\)).

La transposición de una matriz\(A∈R^{m×n}\) es otra matriz\(B\) cuyo elemento en la fila j y columna i es\(b_{ji}=a_{ij}\) para\(1≤i≤m\) y\(1≤j≤n\). Escribimos\(B=A^T\) para indicar que\(B\) es la transposición de\(A\). En MATLAB, la transpuesta se denota con A'. Una forma más intuitiva de describir la operación de transposición es decir que voltea la matriz alrededor de su diagonal principal para que las filas se conviertan en columnas y las columnas se conviertan en filas.

Ejercicio\(\PageIndex{1}\)

Si\(A∈R^{m×n}\), entonces\(A^T∈?\). Encuentra la transposición de la matriz\(A=\begin{bmatrix}2&5\\7&1\\4&9\end{bmatrix}\).

Adición de Matrices y Multiplicación Escalar

Dos matrices del mismo tamaño (en ambas dimensiones) pueden sumarse o restarse de la misma manera que los vectores, sumando o restando los elementos correspondientes. La ecuación\(C=A±B\) significa que para cada\(i\) y\(j,c_{ij}=a_{ij}±b_{ij}\). La multiplicación escalar de una matriz multiplica cada elemento de la matriz por el escalar:

\[aX=\begin{bmatrix} ax_{11} & ax_{12} & ax_{13} & ... & ax_{1n}\\ ax_{21} & ax_{22} & ax_{23} & ... & ax_{2n}\\ ax_{31} & ax_{32} & ax_{33} & ... & ax_{3n}\\ ⠇& ⠇ & ⠇& & ⠇\\ ax_{m1} & ax_{m2} & ax_{m3} & ... & ax_{mn} \end{bmatrix} \nonumber \]

Multiplicación Matricial

Un vector puede considerarse una matriz con una sola columna. Así, intencionalmente difuminamos la distinción entre\(R^{n×1}\) y\(R^n\). También una matriz se puede ver como una colección de vectores, siendo cada columna de la matriz un vector:

\ [\ mathrm {A} =\ left [\ begin {array} {llll}
\ mid &\ mid & & & 1\
\ mathrm {a} _ {1} &\ mathrm {a} _ {2} &\ ldots &\ mathrm {a} _ {n}\\ mid &
\ mid &\ mid &\ end {array}
\ right] =\ left [\ left [\ left [\ left [\ comenzar {array} {l}
a_ {11}\\
a_ {21}\\
\ mid\\
a_ {m 1}
\ end {array}\ derecha]\ left [\ begin {array} {l}
a_ {12}\\
a_ {22}\
\\ mid\
a_ {m 2}
\ end {array}\ right]\ left [\ begin {array} {l}
a_ {1 n}\\
a_ {2 n}\\
\ mediados\\
a_ {m n}
\ end {array}\ derecha]\ derecha]\ nonumber\]

En la operación de transposición, las columnas se convierten en filas y viceversa. La transposición de una\(n×1\) matriz, un vector de columna, es una\(n\) matriz de 1 ×, un vector de fila:

\ [\ mathrm {x} =\ left [\ begin {array} {l}
x_ {1}\\
x_ {2}\\
\ mid\\
x_ {n}
\ end {array}\ derecha];\ mathrm {x} ^ {T} =\ left [x_ {1} x_ {2} x_ {n}\ derecha]\ nonumber\]

Ahora podemos definir la multiplicación matriz-matriz en términos de productos internos de vectores. Empecemos con matrices\(\mathrm{A} \in \mathscr{R}^{m \times n}\) y\(\mathrm{B} \in \mathscr{R}^{n \times p}\). Para encontrar el producto AB, primero divida cada matriz en vectores de columna y vectores de fila de la siguiente manera:

Figura\(\PageIndex{2}\)

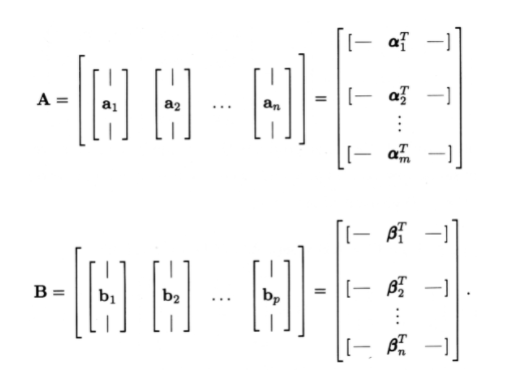
Así\(a_i\) es la\(i^{th}\) columna de A y\(α^T_j\) es la\(j^{th}\) fila de A. Para que se defina la multiplicación matricial, el ancho de la primera matriz debe coincidir con la longitud de la segunda para que todas las filas\(α^T_i\) y columnas\(b_i\) tengan el mismo número de elementos \(n\). El producto de la matriz, C=AB, es una\(m×p\) matriz definida por sus elementos como\(c_{ij}\) =\((α_i,b_j)\). En palabras, cada elemento de la matriz del producto\(c_{ij}\),, es el producto interno de la\(i^{th}\) fila de la primera matriz y la\(j^{th}\) columna de la segunda matriz.

Para n-vectores\(x\) y\(y\), el producto de la matriz\(x^Ty\) adquiere un significado especial. El producto es, por supuesto, una matriz 1×1 (un escalar). El significado especial es que\(x^Ty\) es el producto interno de\(x\) y\(y\):

Figura\(\PageIndex{3}\)

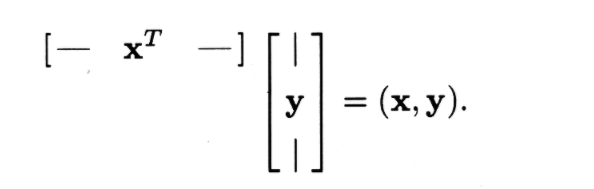
Por lo tanto, la notación\(x^Ty\) se utiliza a menudo en lugar de (x, y). Recordemos de la Demo 1 de “Álgebra Lineal: Otras Normas” que MATLAB utiliza x'* y para denotar producto interno.

Otro caso especial de multiplicación matricial es el producto externo. Al igual que el producto interno, involucra dos vectores, pero esta vez el resultado es una matriz:

Figura\(\PageIndex{4}\)

En el producto exterior, los productos internos que definen sus elementos se encuentran entre vectores de fila unidimensionales de\(x\) y vectores de columna unidimensionales de\(y^T\), es decir, el\((i,j)\) elemento de\(A\) is\(x_iy_j\).

Ejercicio\(\PageIndex{2}\)

Encuentra\(C=AB\) dónde\(A\) y\(B\) son dados por

1. \ (A=\ left [\ begin {array} {lll}
   1 & -1 & 2\\
   3 & 0 & 5
   \ end {array}\ right]\);\ (B=\ left [\ begin {array} {llll}
   0 & -2 & 1 & -3\\
   4 & 2 & 2 & 0\\ 2 & 2 &
   2 & 2 & 2 & 3 & 1
   \ end {array}\ right]\);
2. \ (A=\ left [\ begin {array} {ll}
   1 & 0\\
   0 & 1
   \ end {array}\ right]\);\ (B=\ left [\ begin {array} {llll}
   1 & 2 & 3 & 4\\
   5 & 6 & 7 & 8
   \ end {array}\ right]\);
3. \ (\ mathrm {A} =\ left [\ begin {array} {ccc}
   1 & -1 & -1\\
   1 & 1\\ 1 &
   1 & 1 & 1
   \ end {array}\ right]\);\ (B=\ left [\ begin {array} {lll}
   0 & 3 & 6\\
   1 & 4 & 7\\
   2 y 5 y 8
   \ end {array}\ derecho]\)

Hay varias otras formas equivalentes de definir la multiplicación matricial, y un estudio cuidadoso de la siguiente discusión debería mejorar su comprensión de la multiplicación matricial. Considere\(\mathrm{A} \in \mathscr{R}^{m \times n}\),\(\mathbf{B} \in \mathscr{R}^{n \times p}\), y C=AB para que\(\mathrm{C} \in \mathscr{R}^{m \times p}\). En imágenes, tenemos

\ [m\ left [\ begin {array} {l}
p\\
\ mathrm {C}
\ end {array}\ right] =m\ left [\ begin {array} {l}
n\\
\ mathrm {~A}
\ end {array}\ right]\ left [\ begin {array} {l}
p\\
\ mathrm {~B}
\ end {array}\ right] n\ nonumber\]

En nuestra definición,\(C\) representamos entrada por entrada como

\[\mathrm{c}_{i j}=\left(\alpha_{i}, \mathrm{~b}_{j}\right)=\sum_{k=1}^{n} \mathrm{a}_{i k} b_{k j} \nonumber \]

En imágenes,

Figura\(\PageIndex{5}\)

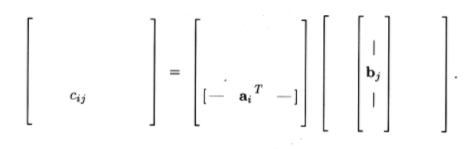
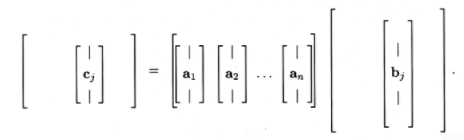
Demostrarás en el Ejercicio 3 que también podemos representar\(C\) en base a columnas:

\[\mathrm{c}_{j}=\sum_{k=1}^{n} \mathrm{a}_{k} b_{k j} \nonumber \]

Figura\(\PageIndex{6}\)

Finalmente, se\(C\) puede representar como una suma de matrices, siendo cada matriz un producto externo:

\[\mathrm{C}=\sum_{i=1}^{n} \mathrm{a}_{i} \beta_{i}^{T} \nonumber \]

Figura\(\PageIndex{7}\)

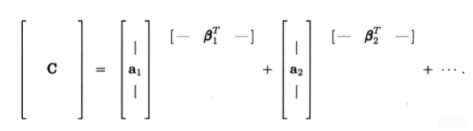
Un ejemplo numérico debería ayudar a aclarar estos tres métodos.

Ejemplo\(\PageIndex{1}\)

Let

\ (A=\ left [\ begin {array} {llll}
1 & 2 & 1 & 3\\
2 & 1 & 2 & 4\\
3 & 3 & 2 & 1
\ end {array}\ right],\ quad B=\ left [\ begin {array} {lll}
1 & 2 & 1\\
2 & 2 & 1\\
1 & 3 & 2\\
2 & 1 & 1 & 1
\ end {array}\ right]\ text {.}\)

Usando el primer método de multiplicación matricial, entrada por entrada, tenemos

\(\mathrm{c}_{i j}=\sum_{k=1}^{4} \mathrm{a}_{i k} b_{k j}\)

o

\ (\ mathrm {C} =\ left [\ begin {array} {lll}
(1\ cdot 1+2\ cdot 2+1\ cdot 1+3\ cdot 2) & (1\ cdot 2+2\ cdot 2+1\ cdot 3+3\ cdot 1) & (1\ cdot 1+2\ cdot 1+1\ cdot 2+3\ cdot 1)\
(2\ cdot 1+1\ cdot 2+2\ cdot 1+4\ cdot 2) & (2\ cdot 2+1\ cdot 2+2\ cdot 3+4\ cdot 1) & (2\ cdot 1+1\ cdot 1+2\ cdot 2+4.1)\\
(3\ cdot 1+3\ cdot 2+2\ cdot 1+1\ cdot 2) & (3\ cdot 2+3\ cdot 2+2\ cdot 3+1\ cdot 1) & (3\ cdot 1+3\ cdot 1+2\ cdot 2+1\ cdot 1)
\ end {array}\ derecha]\)

o

\ (\ mathrm {C} =\ left [\ begin {array} {ccc}
12 & 12 & 8\\
14 & 16 & 11\\
13 & 19 & 11
\ end {array}\ derecha]\)

Sobre una base de columnas,

\(\mathrm{c}_{j}=\sum_{k=1}^{4} \mathrm{a}_{k} b_{k j}\)

\ (\ mathrm {c} _ {1} =\ left [\ begin {array} {l}
1\\
2\
3
\ end {array}\ right] 1+\ left [\ begin {array} {l}
2\\
1\
3
\ end {array}\ right] 2+\ left [\ begin {array} {l}
1\\
2\\
2
\ end {array}\ right] 1+\ left [\ begin {array} {l}
3\\
4\\
1
\ end {array}\ right] 2;\ mathrm {c} _ {2} =\ left [\ begin {array} {l}
1\\
2\
3
\ end {array}\ right] 2+\ left [\ begin {array} {l}
2\\
1\
3
\ end {array}\ right] 2+\ left [\ begin {array} {l}
1\\

2
\ end {array}\ right] 3+\ left [\ begin {array} {l}
3\\
4\\
1
\ end {array}\ right] 1; c_ {3} =\ left [\ begin {array} {l}
1\\
2\
3
\ end {array}\ right] 1+\ left [\ begin {array} {l}
2\\
1\
3\ end {array}
\ right] 1+\ left [\ left [\ begin {array} {l}
1\\
2\\
2
\ end {array}\ right] 2+\ left [\ begin {array} {l}
3\\
4\\
1
\ end {array}\ right] 1\)

Recopilando términos juntos, tenemos

\ (\ begin {array} {c}
\ mathrm {C} =\ left [\ mathrm {c} _ {1}\ mathrm {c} _ {2}\ mathrm {c} _ {3}\ derecha]\
\ mathrm {C} =\ left [\ begin {array} {cc}
(1\ cdot 1+2\ cdot 2+1 cdot 1+3\ cdot 2\ cdot 2) & (1\ cdot 2+2\ cdot 2+1\ cdot 3+3\ cdot 1) & (1\ cdot 1+2\ cdot 1+1\ cdot 2+3\ cdot 1)\\
(2\ cdot 1+1\ cdot 2+2\ cdot 1+4\ cdot 2) & (2\ cdot 2+1\ cdot 2+2\ cdot 3+4\ cdot 1) & (2\ cdot 1+1\ cdot 1+2\ cdot 2+4.1)\\
(3\ cdot 1+3\ cdot 2+2\ cdot 1+1\ cdot 2) & (3\ cdot 1+3\ cdot 2+3\ cdot 2+2\ cdot 3+1\ cdot 1) & (3\ cdot 1+3\ cdot 1+2\ cdot 2+1\ cdot 1)
\ end {array}\ derecha]
\ end {array}\)

Matriz por matriz,

\(\mathrm{C}=\sum_{i=1}^{4} \mathrm{a}_{i} \beta_{i}^{T}\)

\ (C=\ left [\ begin {array} {l}
1\\
2\
3
\ end {array}\ right]\ left [\ begin {array} {lll}
1 & 2 & 1
\ end {array}\ right] +\ left [\ begin {array} {l}
2\\
1\
3
\ end { array}\ derecha]\ left [\ begin {array} {lll}
2 & 2 & 1
\ end {array}\ right] +\ left [\ begin {array} {lll}
1 & 3 & 2
\ end {array}\ right] +\ left [\ begin {array} {l}
1\\
2\
2
\ end {array}\ derecha]\ left [\ begin {array} {lll}
1 & 3 & 2
\ end {array}\ right] +\ left [\ begin {array} {l}
3\\
4\
1
\ end {array}\ right]\ left [\ begin {array} {lll}
1 & 1 & 1
\ end {array}\ right]\)

\ (=\ left [\ begin {array} {lll}
1\ cdot 1 & 1\ cdot 2 & 1\ cdot 1\\ cdot 1\\
2\ cdot 1 & 2\ cdot 2 & 2\ cdot 1\\
3\ cdot 1 & 3\ cdot 1\ cdot 1
\ end {array}\ right] +\ left [\ begin {array} {lll}
2\ punto 2 y 2\ cdot 2 y 2\ cdot 1\\
1\ cdot 2 & 1\ cdot 2 & 1\ cdot 1\\
3\ cdot 2 & 3\ cdot 2 & 3\ cdot 1
\ end {array}\ derecha] +\ izquierda [\ begin {array} {ccc}
1\ cdot 1 & 1\ cdot 3 & 1\ cdot 2\ cdot
2\ cdot 1 & 2\ cdot 3 & 2\ cdot 2\\
2\ cdot 1 & 2\ cdot 3 & 2\ cdot 2\ end {array}
\ derecha] +\ izquierda [\ begin {array} {ccc}
3\ cdot 2 & 3\ cdot 1 & 3\ cdot 1\\ cdot 1\\ 4\ cdot 2 &
4\ cdot 1 & 4\ cdot 1\ cdot 1\ cdot 1 & 4\ cdot 1\ cdot
1 & 4\ cdot 1\ cdot 1 & 4\ cdot 1\ cdot 1
\ end {array}\ derecha]\)

\ (\ mathrm {C} =\ left [\ begin {array} {lll}
(1\ cdot 1+2\ cdot 2+1\ cdot 1+3\ cdot 2) & (1\ cdot 2+2\ cdot 2+1\ cdot 3+3\ cdot 1) & (1\ cdot 1+2\ cdot 1+1\ cdot 2+3\ cdot 1)\
(2\ cdot 1+1\ cdot 2+2\ cdot 1+4\ cdot 2) & (2\ cdot 2+1\ cdot 2+2\ cdot 3+4\ cdot 1) & (2\ cdot 1+1\ cdot 1+2\ cdot 2+4.1)\\
(3\ cdot 1+3\ cdot 2+2\ cdot 1+1\ cdot 2) & (3\ cdot 2+3\ cdot 2+2\ cdot 3+1\ cdot 1) & (3\ cdot 1+3\ cdot 1+2\ cdot 2+1\ cdot 1)
\ end {array}\ derecha]\)

como lo tuvimos en cada uno de los otros casos. Así vemos que los métodos son equivalentes, ¡simplemente formas diferentes de organizar el mismo cálculo!

Ejercicio\(\PageIndex{3}\)

Demostrar que las Ecuaciones 5, 6 y 7 son definiciones equivalentes de multiplicación matricial. Es decir, si C=AB donde\(\mathrm{A} \in \mathscr{R}^{m \times n}\) y\(\mathrm{B} \in \mathscr{R}^{n \times p}\), mostrar que el producto matriz-matriz también se puede definir por

\(c_{i j}=\sum_{k=1}^{n} a_{i k} b_{k j}\)

y, si\(c_k\) es la\(k^{th}\) columna de\(C\) y\(a_k\) es la\(k^{th}\) columna de\(A\), entonces

\(\mathrm{c}_{j}=\sum_{k=1}^{n} \mathrm{a}_{k} b_{k j}\)

Demostrar que la matriz también\(C\) puede escribirse como la ‚ “suma de productos externos”

\(\mathrm{C}=\sum_{k=1}^{n} \mathrm{a}_{k} \beta_{k}^{T}\)

Escribe los elementos en un producto exterior típico\(\mathrm{a}_{k} \beta_{k}^{T} \text { . }\)

Ejercicio\(\PageIndex{4}\)

Dado\(\mathrm{A} \in \mathscr{R}^{m \times n}\),\(\mathrm{B} \in \mathscr{R}^{n \times p}\), y\(\mathrm{C} \in \mathscr{R}^{r \times s}\), para cada uno de los siguientes postulados, ya sea probar que es cierto o dar un contraejemplo que demuestre que es falso:

1. \(\left(\mathrm{A}^{T}\right)^{T}=\mathrm{A}\)
2. \(AB=BA\)cuándo\(n=p\) y\(m=q\). ¿La multiplicación matricial es conmutativa?
3. A (B+C) =AB+AC cuando\(n=p=r\) y\(q=s\). ¿La multiplicación matricial es distributiva sobre la suma?
4. \((\mathrm{AB})^{T}=\mathrm{B}^{T} \mathrm{~A}^{T}\)cuando\(n=p\)
5. (AB) C=A (BC) cuando\(n=p\) y\(q=r\). ¿La multiplicación matricial es asociativa?

Rotación

Ejemplo\(\PageIndex{2}\)

Sabemos por el capítulo sobre números complejos que un número complejo\(z_1=x_1+jy_1\) puede ser girado por ángulo\(\theta\) en el plano complejo formando el producto

\(z_{2}=e^{j \theta} z_{1}\)

Al escribirse, las partes reales e imaginarias de\(z_2\) son

\ (\ begin {alineado}
z_ {2} &=\ qquad\ qquad (\ cos\ theta+j\ sin\ theta)\ izquierda (x_ {1} +j y_ {1}\ derecha)\\
&= (\ cos\ theta) x_ {1} - (\ sin\ theta) y_ {1} +j\ izquierda [(\ sin\ theta) _ {1} + (\ cos\ theta) y_ {1}\ derecha]
\ final {alineado}\)

Si las partes real e imaginaria de\(z_1\) y\(z_2\) están organizadas en vectores\(z_1\) y\(z_2\) como en el capítulo sobre números complejos, entonces la rotación puede llevarse a cabo con la matriz-vector multiplicar

\ (\ mathrm {z} _ {2} =\ left [\ begin {array} {l}
x_ {2}\
y_ {2}
\ end {array}\ right] =\ left [\ begin {array} {ll}
\ cos\ theta & -\ sin\ theta\
\ sin\ theta &\ cos\ theta
\ end {array}\ right]\ left [begin\ {matriz} {l}
x_ {1} \\
y_ {1}
\ end {array}\ derecha]\)

Llamamos a la matriz\ (\ mathrm {R} (\ theta) =\ left [\ begin {array} {ll}
\ cos\ theta & -\ sin\ theta\
\ sin\ theta &\ cos\ theta
\ end {array}\ right]\) una matriz de rotación.

Ejercicio\(\PageIndex{5}\)

Dejar\(R(\theta)\) denotar una matriz de rotación de 2×2. Probar e interpretar las siguientes dos propiedades:

1. \(\mathrm{R}^{T}(\theta)=\mathrm{R}(-\theta)\);
2. \ (\ mathrm {R} ^ {T} (\ theta)\ mathrm {R} (\ theta) =\ mathrm {R} (\ theta)\ mathrm {R} ^ {T} (\ theta) =\ left [\ begin {array} {ll}
   1 & 0\\
   0 & 1
   \ end {array}\ derecha]\)