5.6: Coordenadas homogéneas tridimensionales
- Page ID
- 82374
Consideramos ahora el almacenamiento y manipulación de objetos tridimensionales. Continuaremos usando coordenadas homogéneas para que la traducción pueda ser incluida en operadores compuestos. Las coordenadas homogéneas en tres dimensiones también nos permitirán hacer proyecciones en perspectiva para que podamos ver un objeto tridimensional desde cualquier punto del espacio.
Representación de imagen
La forma tridimensional de la matriz de puntos en coordenadas homogéneas es
\ [\ mathrm {G} =\ left\ {\ begin {array} {lllll}
x_ {1} & x_ {2} & x_ {3} &\ ldots & x_ {n}\\
y_ {1} & y_ {2} & y_ {3} &\ ldots & y_ {n}\\
z_ {1} & z_ {2} & _ {3} &\ ldots & z_ {n}\\
1 & 1 &\ ldots & 1 &\ ldots & 1
\ end {array}\ right\}\ in\ mathscr {R} ^ {4\ times n}\ nonumber\]
La matriz de líneas\(H\) es exactamente como antes, apuntando a pares de columnas\(G\) para conectarse con líneas. Cualquier otra matriz de agrupación para objetos, etc., tampoco se modifica.
Las manipulaciones de imagen se realizan mediante una matriz 4×4\(A\). Para asegurar que la cuarta coordenada siga siendo un 1, el operador\(A\) debe tener la estructura
\ [A=\ left [\ begin {array} {llll}
a_ {11} & a_ {12} & a_ {13} & a_ {14}\\
a_ {21} & a_ {22} & a_ {23} & a_ {24}\\
a_ {31} & a_ {32} & a_ {33} & a_ {34}\\
0 & 0 & 0 & 1
\ end {array}\ derecha]\ nonumber\]
La nueva imagen tiene matriz de puntos
\[\mathrm{G}_{\text {new }}=A G \nonumber \]
Si las coordenadas del\(i^{th}\) punto en\(G\) son\((x_i,y_i,z_i,1)\), ¿cuáles son las coordenadas del\(i^{th}\) punto en\(\mathrm{G}_{\text {new }}=A G\) cuando\(A\) es como se da en la Ecuación 2?
Anote la matriz de puntos\(G\) para el cubo unitario (el cubo con lados de longitud 1, con una esquina en el origen y extendiéndose en la dirección positiva a lo largo de cada eje). Dibuja un boceto del cubo, numerando los vértices según su orden en tu matriz de puntos. Ahora anote la matriz de líneas\(H\) para completar la representación del cubo.
Sistemas de coordenadas para zurdos y diestros
En este libro trabajamos exclusivamente con sistemas de coordenadas diestros. No obstante, cabe señalar que existen dos formas de disponer los ejes en tres dimensiones. La Figura 1 (a) muestra las coordenadas habituales para diestros, y la variación para zurdos se muestra en la Figura 1 (b). Todas las opciones posibles de etiquetas\(x\)\(y\),, y\(z\) para los tres ejes de coordenadas se pueden girar para ajustarse a una de estas dos figuras, pero ninguna rotación irá de una a otra.
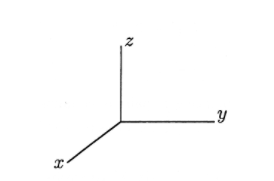 (a)
(a)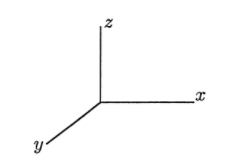 b)
b)Tenga cuidado de esbozar un sistema de coordenadas diestro cuando esté resolviendo problemas en este capítulo. Algunas respuestas no serán las mismas para un sistema zurdo.
Transformación de imagen
Las operaciones tridimensionales son un poco más complicadas que sus contrapartes bidimensionales. Para escalar y traducir ahora tenemos tres direcciones independientes, por lo que generalizamos los operadores de la Ecuación 10 a partir de “Gráficos vectoriales: Coordenadas homogéneas” como
\ [\ mathrm {S}\ izquierda (s_ {x}, s_ {y}, s_ {z}\ derecha) =\ izquierda\ {\ begin {array} {llll}
s_ {x} & 0 & 0 & 0\\
0 & s_ {y} & 0 & 0\\
0 & 0 & s_ {z} & 0\\
0 & 0 & 0 & 1
\ end array}\ derecha\}\ nonumber\]
\ [\ mathrm {T}\ left (t_ {x}, t_ {y}, t_ {z}\ derecha) =\ left [\ begin {array} {llll}
1 & 0 & 0 & t_ {x}\\
0 & 1 & 0 & t_ {y}\\
0 & 0 & 0 & 0 & 1 & t_ {z}\\
0 & 0 & 0 & 1
\ end {array}\ derecha]\ texto {.}\ nonumber\]
Demostrar que T\((−t_x,−t_y,−t_z)\) es la inversa de T\((t_x,t_y,t_z)\. T\(^{-1}\) deshace el trabajo de\(T\).
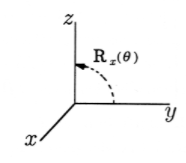
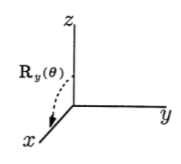
La rotación se puede hacer sobre cualquier línea arbitraria en tres dimensiones. Vamos a construir hasta el caso general presentando primero los operadores que rotan alrededor de los tres ejes de coordenadas. R\(_x(\theta)\) gira en ángulo\(\theta\) alrededor del eje x, con positivo\(\theta\) que va del eje y al eje z, como se muestra en la Figura 2. De manera similar, la rotación positiva alrededor del eje y usando R\(_y(\theta)\) va de\(z\) a\(x\), y la rotación positiva alrededor del eje z va de\(x\) a\(y\), al igual que en dos dimensiones. Tenemos las rotaciones fundamentales
\ [\ mathrm {R} _ {x} (\ theta) =\ left\ {\ begin {array} {llll}
1 & 0 & 0 & 0 & 0\\
0 &\ cos\ theta & -\ sin\ theta & 0\\
0 &\ sin\ theta &\ cos\ theta & 0\\ 0 &
0 & 0 & 0 & 1
\ end {array}\ derecha\}\ nonumba er\]
\ [\ mathrm {R} _ {y} (\ theta) =\ left\ {\ begin {array} {llll}
\ cos\ theta & 0 &\ sin\ theta & 0\\ 0 &
0 & 0 & 0 & 0\
-\ sin\ theta & 0 &\ cos\ theta & 0\\ 0 &
0 & 0 & 0 & 1
\ end {array}\ right\}\ nonumber er\]
\ [\ mathrm {R} _ {z} (\ theta) =\ left\ {\ begin {array} {llll}
\ cos\ theta & -\ sin\ theta & 0 & 0\\\ sin
\ theta &\ cos\ theta & 0 & 0 & 0\\ 0 &
0 & 0 & 0 & 0 & 0 &
0 & 0 & 0 & 1
\ end {array}\ right\}\ nonumber er\]
Se puede construir una rotación más general sobre cualquier línea a través del origen mediante la composición de las tres rotaciones fundamentales. Finalmente, componiendo la traslación con las rotaciones fundamentales, podemos construir un operador que gire alrededor de cualquier línea arbitraria en el espacio.
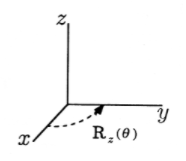
Para rotar en ángulo\(\psi\) alrededor de la línea\(\mathscr{L}\), que se encuentra en el\(x−y\) plano de la Figura 3, haríamos
- girar\(\mathscr{L}\) al eje x con R\(_z(−\theta)\);
- rotar\(\psi\) alrededor del eje x con R\(_x(\psi)\); y
- girar de nuevo a\(\mathscr{L}\) con R\(_z(\theta)\).
La operación compuesta sería
\[\mathrm{A}(\theta, \varphi)=\mathrm{R}_{z}(\theta) \mathrm{R}_{x}(\varphi) \mathrm{R}_{z}(-\theta) \nonumber \]

Dirección Cosines
Como se discute en el capítulo sobre Álgebra Lineal, un vector vv puede especificarse por sus coordenadas\((x,y,z)\) o por su longitud y dirección. La longitud de\(\nu\) es ||\(\nu\) ||, y la dirección se puede especificar en términos de los tres cosenos de dirección\((\cos{\theta_x}, \cos{\theta_y}, \cos{\theta_z})\). El ángulo\(\theta_x\) se mide entre el vector\(\nu\) y el eje x o, de manera equivalente, entre el vector\(\nu\) y el vector\(e_x=[100]^T\). Tenemos
\[\cos \theta_{x}=\frac{\left(\mathrm{v}, \mathrm{e}_{x}\right)}{\|\mathrm{v}\|\left\|\mathrm{e}_{x}\right\|}=\frac{x}{\|\mathrm{v}\|} \nonumber \]
Asimismo,\(\theta_y\) se mide entre\(\nu\) y\(e_y=[010]^T\), y\(\theta_z\) se mide entre\(\nu\) y\(e_z=[001]^\). Así
\[\cos \theta_{y}=\frac{y}{\|\mathrm{v}\|} \nonumber \]
\[\cos \theta_{z}=\frac{z}{\|v\|} \nonumber \]
El vector
\ [\ mathrm {u} =\ left\ {\ begin {array} {c}
\ cos\ theta_ {x}\\
\ cos\ theta_ {y}\\
\ cos\ theta_ {z}
\ end {array}\ derecha\}\ nonumber\]
s un vector de unidad en la dirección de\(\nu\), así que tenemos
\ [\ mathrm {v} =\ |\ mathrm {v}\ |\ mathrm {u} =\ |\ mathrm {v}\ |\ left\ {\ begin {array} {l}
\ cos\ theta_ {x}\\
\ cos\ theta_ {y}\\
\ cos\ theta_ {z}
\ end {array}\ derecha\}\ nonumber\]
Mostrar que\(u\) es un vector unitario (es decir, 1 u||=1u||=1).
Los cosenos de dirección son útiles para especificar una línea en el espacio. En lugar de dar dos puntos\(P_1\) y\(P_2\) en la línea, podemos dar un punto\(P_1\) más los cosenos de dirección de cualquier vector que apunte a lo largo de la línea. Uno de esos vectores es el vector de\(P_1\) a\(P_2\).
Tangentes de arco
Considera un vector\ (\ mathrm {v} =\ left\ {\ begin {array} {l}
x\\
y
\ end {array}\ right\}\) en dos dimensiones. Sabemos que
\[\tan \theta=\frac{y}{x} \nonumber \]
para el ángulo\(\theta\) mostrado en la Figura 4. Si sabemos\(x\) y\(y\), podemos encontrar\(\theta\) usando la función de arco tangente
\[\theta=\tan ^{-1}\left(\frac{y}{x}\right) \nonumber \]
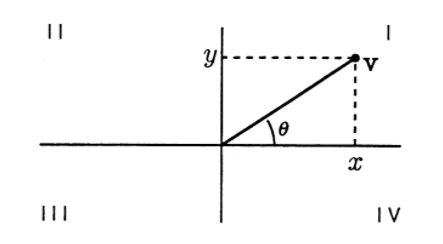
En MATLAB,
theta = atan(y/x)
Desafortunadamente, la tangente de arco siempre da respuestas entre\(−\frac{\pi}{2}\) y\(\frac{\pi}{2}\) correspondientes a puntos\(\nu\) en los cuadrantes I y IV. El problema es que la relación\(\frac{-y}{-x}\) es la misma que la relación −−−\(x\) A por lo que el cuadrante III no puede distinguirse del cuadrante I por la relación.\(\frac{y}{x}\) Asimismo, los cuadrantes II y IV son indistinguibles.
La solución es la función de arco tangente de dos argumentos. En MATLAB,
theta = atan2(y,x)
dará el ángulo verdadero\(\theta\)\(-\pi\) y\(\pi\) en cualquiera de los cuatro cuadrantes.
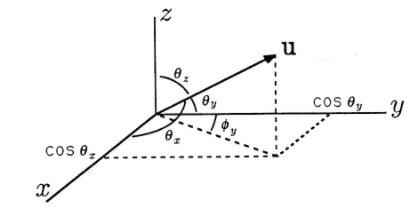
Considere el vector de dirección\ (\ mathrm {u} =\ left\ {\ begin {array} {l}
\ cos\ theta_ {x}\\
\ cos\ theta_ {y}\\
\ cos\ theta_ {z}
\ end {array}\ right\}\) como se muestra en la Figura 5. ¿Cuál es el ángulo\(\psi_y\) entre la proyección de\(u\) dentro del\(x−y\) plano y el eje y? Esto es importante porque es R la\(_z(\psi_y)\) que va a poner\(u\) en el\(y−z\) plano, y necesitamos conocer el ángulo\(\psi_y\) para poder llevar a cabo esta rotación. Primero tenga en cuenta que no es lo mismo que\(\theta_y\). A partir de la geometría de la figura, podemos escribir
\[\tan \varphi_{y}=\frac{\cos \theta_{x}}{\cos \theta_{y}} \nonumber \]
Esto nos da una fórmula para\(\psi_y\) en términos de la dirección cosenos de\(u\). Con la tangente de arco de dos argumentos, podemos escribir
\[\varphi_{y}=\tan ^{-1}\left(\cos \theta_{x}, \cos \theta_{y}\right) \nonumber \]
- Supongamos que el punto\(p'\) está en el\(y−z\) plano en tres dimensiones,\(p′=(0,y′,'',1)\). Encuentra\(\theta\) para que R\(_x(\theta)\) rote\(p'\) al eje z positivo. (Pista: Usa la tangente de arco de dos argumentos. \(\theta\)será una función de\(y'\) y\(z'\).)
- Dejar\(p\) ser cualquier punto en el espacio tridimensional,\(p=(x,y,z,1)\). Encuentra\(\psi\) para que R\(_z(\psi)\) gira\(p\) hacia el\(y−z\) plano. (Pista: Dibuje la situación en tres dimensiones, luego dibuje una vista bidimensional mirando hacia abajo en el\(x−y\) plano desde el eje z positivo. Comparar con el Ejemplo 2.) Sus respuestas a las partes (a) y (b) se pueden componer en un operador Z (p) que gira un punto dado\(p\) al eje z positivo, Z (p)\(_x(\theta)\) =R\(_z(\psi)\) R.
- Dejar\(\mathscr{L}\) ser una línea en el espacio tridimensional especificada por un punto 1 =\((x,y,z,1)\) y los cosenos de dirección\((\cos{\theta_x}, \cos{\theta_y}, \cos{\theta_z})\). Utilice el siguiente procedimiento para derivar un operador compuesto R\((\psi,\mathscr{L})\) que gira en ángulo\(\psi\) alrededor de la línea\(\mathscr{L}\):
- traducir 1 al origen;
- let u=\((\cos{\theta_x}, \cos{\theta_y}, \cos{\theta_z}, 1)\) y use Z (u) para alinearse\(\mathscr{L}\) con el eje z;
- rotar\(\psi\) alrededor del eje z;
- deshacer la etapa (ii); y
- deshacer paso (i)


