7.4: Códigos Huffman para Codificación Fuente

Última actualización
Guardar como PDF

Page ID: 82332

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

En 1838, Samuel Morse estaba luchando con el problema de diseñar un código eficiente para transmitir información a través de líneas telegráficas. Razonó que un código eficiente usaría palabras de código corto para letras comunes y palabras de código largas para letras poco comunes. (¿Puedes ver el motivo de lucro en el trabajo?) Para convertir este principio razonado en práctica viable, Morse rebuscó en las charolas de composición para tipografía en una imprenta. Descubrió que los tipógrafos usan muchos\(e′s\) más de s. Posteriormente formó una tabla que mostraba la frecuencia relativa con la que se utilizó cada letra. Su ingenioso código Morse de longitud variable asignaba códigos cortos a letras probables (como “punto” para\(e'\)) y códigos largos a letras poco probables (como “dash dash dot dot” para\(z'\)). Ahora sabemos que Morse estuvo dentro de aproximadamente el 15% del mínimo teórico para la longitud promedio de las palabras clave para el texto en inglés.

Una variación en el experimento de Morse

Con el fin de sentar las bases para nuestro estudio de códigos fuente eficientes, hagamos una variación del experimento de Morse para ver si podemos llegar de forma independiente a una forma de diseñar códigos. En lugar de darnos una bandeja de composición, comencemos con una fuente de comunicación que genere cinco símbolos o letras\(S_0,S_1,S_2,S_3,S_4\). Ejecutamos la fuente para 100 transmisiones y observamos los siguientes números de transmisiones para cada símbolo:

\ [\ begin {align}
50\ quad S_ {0} ^ {\ prime}\ mathrm {s}\ nonumber\\
20\ quad S_ {1} ^ {\ prime}\ mathrm {s}\ nonumber\\
20\ quad S_ {2} ^ {\ prime}\ mathrm {s}\\
5\ quad S_ {3} ^ {\ prime}\ mathrm {s}\ nonumber\\
5\ quad S_ {4} ^ {\ prime}\ mathrm {s}\ nonumber.
\ end {align}\ nonumber\]

Supondremos que estas “estadísticas de origen” son típicas, es decir, que 1000 transmisiones producirían\(S_0\) 500's y así sucesivamente.

El código binario más primitivo que podríamos construir para nuestra fuente usaría tres bits para cada símbolo:

\ (\ begin {array} {r}
S_ {0}\ sim 000\\
S_ {1}\ sim 001\\
S_ {2}\ sim 010\\
S_ {3}\ sim 011\\
S_ {4}\ sim 100\\
x\ sim 101\\
x\ sim 110\\
x\ sim 111.
\ end {array}\)

Este código es ineficiente de dos maneras. En primer lugar, deja tres palabras de código ilegales que no corresponden a ningún símbolo fuente. Segundo, usa la misma longitud de palabra de código para un símbolo poco probable (like\(S_4\)) que usa para un símbolo probable (like\(S_0\)). El primer defecto podemos corregir concatenando símbolos consecutivos en bloques de símbolos, o símbolos compuestos. Si formamos un símbolo compuesto que consiste en símbolos de\(M\) origen, entonces un símbolo compuesto típico es\(S_1 S_0 S_1 S_4 S_2 S_3 S_1 S_2 S_0\). El número de tales símbolos compuestos que se pueden generar es\(5^M\). El código binario para estos símbolos\(5^M\) compuestos debe contener dígitos\(N\) binarios donde

\(2^{N-1}<5^{M}<2^{N}\left(N \cong M \log _{2} 5\right)\)

El número de bits por símbolo de origen es

\(\frac{N}{M} \cong \log _{2} 5=2.32\)

Este esquema mejora el mejor código de longitud variable de la Tabla 2 de “Códigos binarios: De símbolos a códigos binarios” en 0.08 bits/símbolo.

Ejercicio\(\PageIndex{1}\)

Supongamos que su fuente de información genera las 26 letras romanas minúsculas utilizadas en el texto en idioma inglés. Estas letras deben ser concatenadas en bloques de longitud\(M\). Complete la siguiente tabla de\(N\) (número de bits) versus\(M\) (número de letras en un bloque) y muestre que\(\frac{N}{M}\) se acerca\(\log_2 26\).

	\(M\)
	\ (M\)” class="lt-eng-9992">1	2	3	4	5	6
\(N\)	\ (M\)” class="lt-eng-9992">5	10
\(N/M\)	\ (M\)” class="lt-eng-9992">5	5

Ahora razonemos, como lo hizo Morse, que un código eficiente usaría códigos cortos para símbolos probables y códigos largos para símbolos poco probables. Escojamos el código #5 de la Tabla 2 de “Códigos Binarios: De Símbolos a Códigos Binarios” para este propósito:

\ (\ begin {array} {ccccc}
S_ {0} & S_ {1} & S_ {2} & S_ {3} & S_ {4}\\
1 & 01 & 001 & 0001 & 0000
\ end {array}\)

Este es un código de longitud variable. Si usamos este código en los 100 símbolos que generaron nuestra estadística de origen, el número promedio de bits/símbolo es

\(\frac{1}{100}[50(1)+20(2)+20(3)+5(4)+5(4)]=1.90 \mathrm{bits} / \mathrm{symbol}\)

Ejercicio\(\PageIndex{2}\)

Utilice las estadísticas de origen de la Ecuación 1 para determinar el número promedio de bits/símbolo para cada código en la Tabla 2 de “Códigos binarios: De símbolos a códigos binarios”.

Entropía

Hasta el momento, cada esquema ad hoc que hemos probado ha producido una mejora en el número promedio de bits/símbolo. ¿Hasta dónde puede llegar esto? La respuesta viene dada por el teorema de codificación fuente de Shannon, que dice que el número mínimo de bits/símbolo es

\[\frac{N}{M} \geq-\sum_{i=1}^{M} p_{i} \log _{2} p_{i} \nonumber \]

donde\(p_i\) está la probabilidad de que\(S_i\) se genere símbolo y\(-\sum p_{i} \log _{2} p_{i}\) es una propiedad fundamental de la fuente llamada entropía. Para nuestro ejemplo de cinco símbolos, la tabla de\(p_i\) y\(-\log p_{i}\) se da en la Tabla 2. La entropía es 1.861, y el límite en bits/símbolo es

\(\frac{N}{M} \geq 1.861\)

El código #5 viene dentro de 0.039 de este límite inferior. Como veremos en los siguientes párrafos, esto es lo más cercano que podamos llegar sin codificar símbolos compuestos.

Tabla 1: Estadísticas de origen para Fuente de Cinco Símbolos
Símbolo	Probabilidad	~ Probabilidad de registro
\(S_0\)	0.5	1
\(S_1\)	0.2	2.32
\(S_2\)	02	2.32
\(S_3\)	0.05	4.32
\(S_4\)	0.05	4.32

Ejercicio\(\PageIndex{3}\)

Seleccione una página arbitraria de texto en inglés. Construir una tabla de estadísticas de origen que contenga\(p_i\) (frecuencias relativas) y\(-\log p_{i}\) para\(a\) a través\(z\). (Ignorar la distinción entre mayúsculas y minúsculas e ignorar la puntuación y otros símbolos especiales). Calcula la entropía\(-\sum_{i=1}^{26} p_{i} \log _{2} p_{i}\).

Códigos Huffman

A finales de la década de 1950, David Huffman descubrió un algoritmo para diseñar códigos de longitud variable que minimizan el número promedio de bits/símbolo. El algoritmo de Huffman utiliza un principio de optimalidad que dice, “el código óptimo para\(M\) las letras ha embebido en él el código óptimo para las\(M-1\) letras que resultan de agregar los dos símbolos menos probables”. Cuando se itera este principio, entonces tenemos un algoritmo para generar el árbol binario para un código Huffman:

etiquetar todos los símbolos como “hijos”;
“gemelar” los dos hijos menos probables y darle al gemelo la suma de las probabilidades:

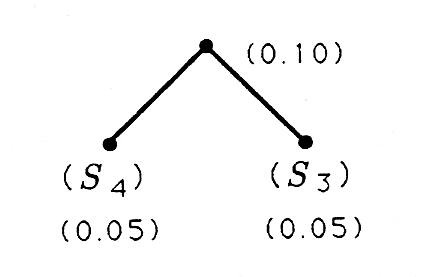
(considerar al gemelo como un niño; y
repetir los pasos ii) y iii) hasta que se contabilice a todos los niños.

Este árbol ahora está etiquetado con 1's y 0's para obtener el código Huffman. El procedimiento de etiquetado es etiquetar cada rama derecha con un 1 y cada rama izquierda con un 0. El procedimiento para diseñar símbolos y construir árboles y códigos de Huffman se ilustra en los siguientes ejemplos.

Ejemplo\(\PageIndex{1}\)

Considerar las estadísticas de origen

\ (\ begin {array} {cccccc}
\ text {Símbolo} & S_ {0} & S_ {1} & S_ {2} & S_ {3} & S_ {4}\
\ text {Probabilidad} & 0.5 & 0.2 & 0.2 & 0.05 & 0.05
\ end {array}\)

para lo cual el algoritmo Huffman produce el siguiente árbol binario y su código correspondiente:

Ejemplo\(\PageIndex{2}\)

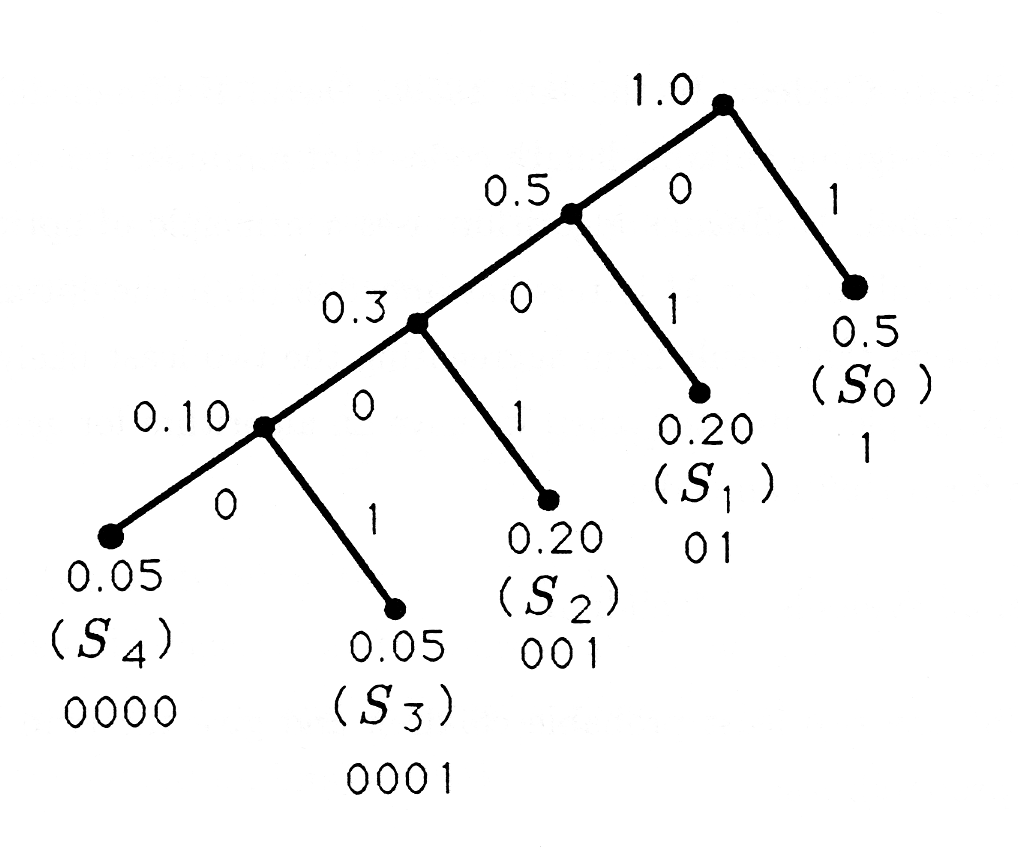
El código Huffman para las estadísticas de origen

\ (\ begin {array} {cccccc}
\ text {Símbolo} & S_ {0} & S_ {1} & S_ {2} & S_ {3} & S_ {4}\
\ text {Probabilidad} & 0.75 & 0.075 & 0.075 & 0.05 & 0.05
\ end {array}\)

se ilustra a continuación:

Ejercicio\(\PageIndex{4}\)

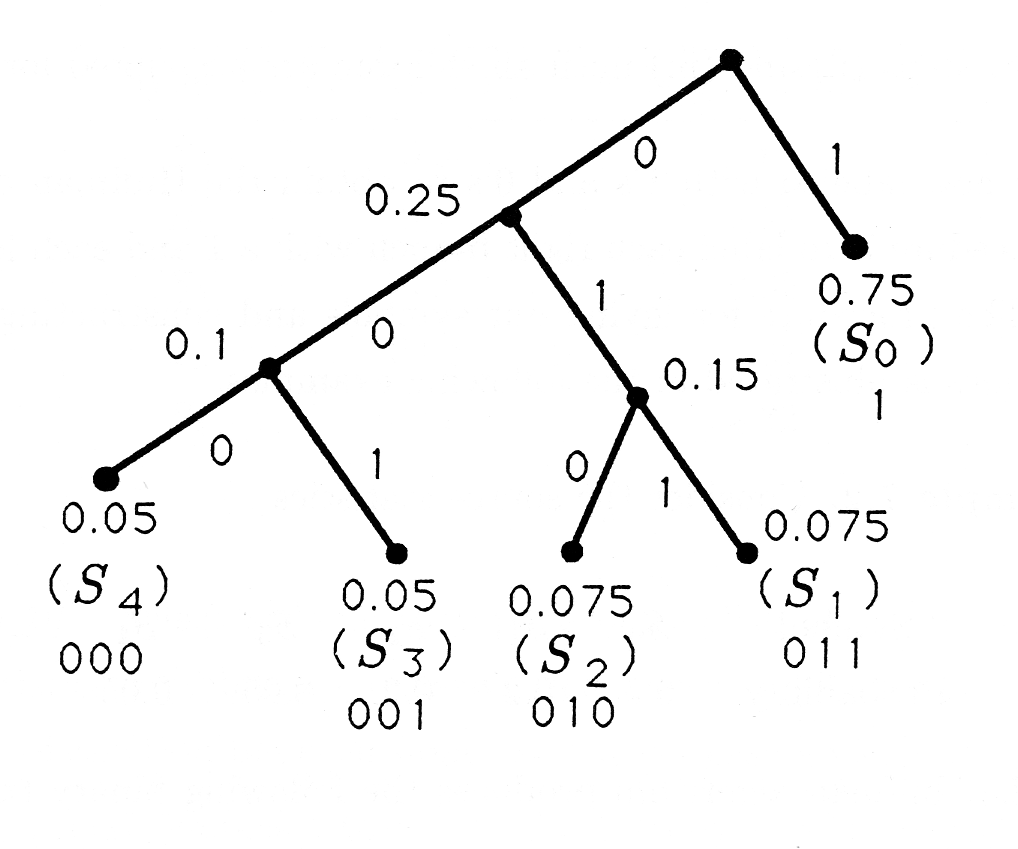
Genere árboles binarios y códigos Huffman para las siguientes estadísticas fuente:

\ (\ begin {array} {ccccccccc}
\ text {Símbolo} & S_ {0} & S_ {1} & S_ {2} & S_ {3} & S_ {4} & S_ {5} & S_ {6} & S_ {7}\
\ text {Probabilidad1} & 0.20 & 0.20 & 0.15 & 0.15 & 0.1 & 0.1 & 0.05 & 0.05\\
\ texto { Probabilidad2} & 0.3 & 0.25 & 0.1 & 0.1 & 0.075 & 0.075 & 0.05 & 0.05
\ end {array}\)

Codificar una máquina de fax

Los símbolos pueden surgir de formas inusuales y definirse de manera bastante arbitraria. Para ilustrar este punto, consideramos el diseño de una hipotética máquina de FAX. Para nuestro diseño asumiremos que un escáner láser lee una página de texto o imágenes en blanco y negro, produciendo un alto voltaje para una mancha negra y una baja tensión para una mancha blanca. También asumiremos que el escáner láser resuelve la página en 1024 líneas, con 1024 puntos/línea. Esto significa que cada página está representada por una matriz bidimensional, o matriz, de píxeles (elementos de imagen), siendo cada píxel 1 o 0. Si simplemente transmitiéramos estas l y O′s, entonces necesitaríamos 1024×1024=1,059,576 bits. Si estos se transmitieran a través de una línea telefónica de 9600 baudios, entonces tardarían casi 2 minutos en transmitir el FAX. Esto es mucho tiempo.

Pensemos en una línea de escaneo típica para una página impresa. Contendrá tiradas largas de 0's, correspondientes a tiradas largas de blanco, interrumpidas por ráfagas cortas de l's, correspondientes a tiradas cortas de negro donde el escáner encuentra una línea o una parte de una letra. Entonces, ¿por qué no tratar de definir un símbolo para que sea “una racha de\(k\) 0's” y codificar estas carreras? El código resultante se llama “código de longitud de ejecución”. Definamos ocho símbolos, correspondientes a longitudes de ejecución de 0 a 7 (una longitud de ejecución de 0 es un 1):

\ (\ begin {aligned}
&S_ {0} =\ text {longitud de ejecución de} 0\ text {ceros} (a 1)\\
&S_ {1} =\ quad\ text {longitud de ejecución de} 1\ text {cero}\\
&\ vdots\\
&S_ {7} =\ text {longitud de ejecución de} 7\ text {ceros.}
\ end {alineado}\)

Si simplemente usáramos un código binario simple de tres bits para estos ocho símbolos, entonces para cada línea de escaneo generaríamos desde 3×1024 bits (para una línea de escaneo que consta de todos los 1) hasta 3 × 1024/7\(\cong\) 400 bits (para una línea de escaneo que consta de todos los 0's). Pero, ¿y si ejecutamos un experimento para determinar la frecuencia relativa de las longitudes de ejecución\(S_7\) y\(S_0\) usamos un código Huffman para “codificar por longitud de ejecución” las longitudes de ejecución? El siguiente problema explora esta posibilidad y produce un código de FAX eficiente.

Ejercicio\(\PageIndex{5}\)

Un experimento realizado en documentos FAXed produce las siguientes estadísticas para longitudes de tiradas de blanco que van de 0 a 7:

\ (\ begin {array} {ccccccccc}
\ text {Símbolo} & S_ {0} & S_ {1} & S_ {2} & S_ {3} & S_ {4} & S_ {5} & S_ {6} & S_ {7}
\\ text {Probabilidad} & 0.01 & 0.06 & 0.1 & 0.1 & 0.2 & 0.15 & 0.2
\ end {array}\)

Estas estadísticas indican que sólo el 1% de una página típica es negra. Construye el código Huffman para esta fuente. Usa tu código Huffman para codificar y decodificar estas líneas de escaneo: