7.5: Códigos Hamming para codificación de canales
- Page ID
- 82346
La idea detrás de los códigos de Hamming es intercalar, o agregar, dígitos binarios adicionales a un código binario para que puedan detectarse y corregirse errores en la transmisión del código a través de un canal. Por ejemplo, supongamos que transmitimos el código 01101001, y se recibe como 01001001. En esta transmisión, el tercer bit más significativo se recibe erróneamente. Definamos la siguiente “adición de módulo-2" de números binarios:
\ (\ comenzar {reunido}
0\ oplus 0=0\\
0\ oplus 1=1\\
1\ oplus 0=1\\
1\ oplus 1=0
\ final {reunido}\)
La multiplicación en aritmética módulo-2 es simplemente\(0 \cdot 0=0 \cdot 1=1 \cdot 0=0 \text { and } 1 \cdot 1=1\). Entonces podemos decir que la secuencia de error 00100000 se “agrega” a la transmisión 01101001 para producir la recepción errónea:
\ (\ begin {align} 01101001 &\ quad transmitido\ nonumber\
\ oplus\ quad 00100000 &\ qquad error\ nonumber\\
01001001 &\ quad recibido. \ nonumber\ end {align}\)
Los códigos de corrección de errores de Hamming nos permitirán recibir la transmisión errónea y detectar y corregir el error. Esto es obviamente de gran valor para transmitir y almacenar información. (Imagínese lo molesto que estaría al tener el código binario de su cuenta corriente confundido con el de la señora Joan Kroc.)
Elegir el número de bits de comprobación
Supongamos que tenemos\(N\) bits de información que deseamos transmitir y que deseamos intercalar “bits de verificación” que nos permitan detectar y corregir cualquier error de un solo bit en la transmisión. Si usamos bits de\(N\) información y bits de verificación nn, entonces transmitiremos una palabra de código que contenga\(N+n\) bits. Los bits de\(n\) verificación pueden codificar\(2^n\) eventos, y queremos que estos eventos indiquen si se produjeron o no errores y, en caso afirmativo, dónde ocurrieron. Por lo tanto, requerimos dónde\((N+n)\) está el número de eventos de error único que pueden ocurrir y +1 es el número de eventos sin error. Por ejemplo, cuando\(N=4\), requerimos\(n=3\) para que\(2^3 \geq (4+3)+1\).
¿Cuántos bits de verificación requiere para codificar siete bits de información para una sola corrección de error?
Construcción de código
Supongamos que hemos construido un código\((N,n)\) Hamming que consiste en bits de\(N\) información y bits de\(n\) verificación (o bits de paridad). Denotamos los bits de información por\(x_{1}, x_{2}, \ldots, x_{N}\) y los bits de verificación por\(c_{1}, c_{2}, \ldots, c_{n}\). Estos bits pueden estar intercalados. Cuando\(N=4\) y\(n=3\), entonces una matriz típica de bits dentro de una palabra de código sería una de las siguientes:
\ (\ left [\ begin {array} {l}
c_ {1}\\
c_ {2}\\
x_ {1}\\
c_ {3}\\
x_ {2}\\
x_ {3}\\
x_ {4}
\ end {array}\ right]\ quad\ text {o}\ quad\ left [\ begin {array} {l}
x_ {1}\\
x_ { 2}\\
x_ {3}\\
x_ {4}\\
c_ {1}\\
c_ {2}\\
c_ {3}
\ end {array}\ derecha]\)
El primer ordenamiento es “natural” (como veremos), y el segundo es “sistemático” (término que se utiliza para describir cualquier código cuya cabeza sea información y cuya cola sea check). Si ocurre un solo error en un\((N,n)\) código, entonces la palabra de código recibida será la suma modulo-2 de la palabra de código y la palabra de error que contiene un 1 en su\(i^{\text{th}}\) posición:
\ [\ left [\ begin {array} {l}
c_ {1}\\
c_ {2}\\
x_ {1}\\
c_ {3}\\
x_ {2}\\
x_ {3}\\
x_ {4}
\ end {array}\ derecha]\ oplus\ left [\ begin {array} {l}
0\\
0\
1\\
0\\
0\\
0
\ end {array}\ derecha]\ nonumber\]
Nos gustaría operar en esta palabra de código recibida de tal manera que se pueda determinar la ubicación del bit de error. Si no hubiera palabra clave, entonces una solución obvia sería premultiplicar la palabra de error por la matriz de verificación de paridad
\ [\ begin {align}
&A^ {T} =\ left [\ begin {array} {lllllll}
1 & 0 & 1 & 0 & 1 & 0 & 1\
0 & 1\ 0 & 1 & 1 & 0 & 1 &
0 & 1 & 1 & 1 & 1 & 1 & 1 & 1
\ end {array}\ derecha]\\
&\ quad [(1)\ quad (2)\ quad (3)\ quad (4)\ quad (5)\ quad (6)\ quad (7)]\ nonumber
\ end {align}\ nonumber\]
La\(i^{\text{th}}\) columna de\(A^T\) es solo el código binario para\(i\). Cuando\(A^T\) premultiplica una palabra de error, el bit de error selecciona la columna que codifica la posición de error:
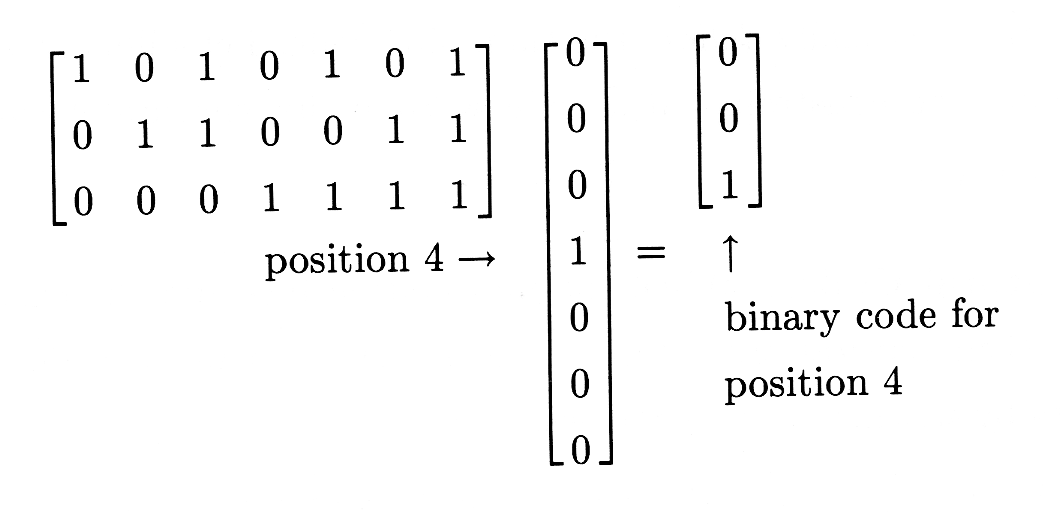
Si la palabra de error no contiene bits de error, entonces el producto es 0, lo que indica que no hay errores.
Esto parece una buena idea, pero ¿qué pasa con el efecto de la palabra clave? En el Ejercicio 1, se le pide que demuestre que el efecto de la matriz de comprobación de paridad\(A^T\) aplicada a la suma módulo-2 de una palabra clave\(x\) y una palabra de error\(e\) es
\[\mathrm{A}^{T}(\mathrm{x} \oplus \mathrm{e})=\mathrm{A}^{T} \mathrm{x} \oplus \mathrm{A}^{T} \mathrm{e} \nonumber \]
En esta ecuación todas las sumas y productos obedecen a las reglas de la aritmética módulo-2.
Dejar\(y=x \oplus e\) denotar la suma módulo-2 de una palabra de código\(x\) y una palabra de error e;\(A^T\) es una matriz de comprobación de paridad. Demostrar que
\(\mathrm{A}^{T} \mathrm{y}=\mathrm{A}^{T} \mathrm{x} \oplus \mathrm{A}^{T} \mathrm{e}\)
Hemos diseñado la matriz de comprobación de paridad\(A^T\) para que el síndrome\(A^Te\) produzca un código binario para la ubicación del error. (La ubicación del error es el síndrome de la palabra de error). El producto\(A^Tx\) interferirá con este síndrome a menos que\(A^Tx\) =0. Por lo tanto, requeriremos que la palabra clave\(x\) satisfaga la restricción
\[\mathrm{A}^{T} \mathrm{x}=0 \nonumber \]
Esta restricción en realidad define el código de Hamming. Ilustremos este punto aplicando la restricción a una palabra clave en su “formato natural”\(\mathrm{x}^{T}=\left(c_{1} c_{2} x_{1} c_{3} x_{2} x_{3} x_{4}\right)\).
Códigos Naturales
Cuando los bits de información y los bits de verificación se codifican en su orden natural\(\left(c_{1} c_{2} x_{1} c_{3} x_{2} x_{3} x_{4}\right)\), entonces podemos determinar los bits de verificación escribiendo de la\(A^Tx\) siguiente manera:
\ [\ left [\ begin {array} {lllllll}
1 & 0 & 1 & 0 & 1 & 0 & 1\\
0 & 1 & 1 & 0 & 0 & 0 & 1 & 1\\
0 & 0 & 0 & 1 & 1 & 1 & 1
\ end {array}\ derecha]\ left [\ begin {array} {l}
c_ {1}\\
c_ {2}\\
x_ {1}\\
c_ {3}\\
x_ {2}\\
x_ {3}\\
x_ {4}
\ end {array}\ right] =\ left [\ begin {array} {l}
0\\
0
\ end {array}\\ derecha]\ nonumber\]
Utilizamos las reglas de la aritmética módulo-2 para escribir estas restricciones como
\ [\ begin {align}
&c_ {1}\ oplus x_ {1}\ oplus x_ {2}\ oplus x_ {4} =0\\
&c_ {2}\ oplus x_ {1}\ oplus x_ {3}\ oplus x_ {4} =0\\
&c_ {3}\ oplus x_ {2}\ oplus x_ {3}\ oplus x_ {4} =0
\ end {align}\ nonumber\]
Por lo tanto los bits de verificación\(c_1,c_2\), y\(c_3\) son simplemente las siguientes sumas de módulo-2
\ [\ begin {align}
c_ {1} &=x_ {1}\ oplus x_ {2}\ oplus x_ {4}\\
c_ {2} &=x_ {1}\ oplus x_ {3}\ oplus x_ {4}\
c_ {3} &=x_ {2}\ oplus x_ {3}\ oplus x_ {3}\ oplus x_ {4}}
\ end {align}\ nonumber\]
Este hallazgo puede organizarse en la ecuación matricial
\ [\ left [\ begin {array} {l}
c_ {1}\\
c_ {2}\\
x_ {1}\\
c_ {3}\\
x_ {2}\\
x_ {3}\\
x_ {4}
\ end {array}\ derecha] =\ left [\ begin {array} {l}
1101\\
1011\
1000 \\
0111\\
0100\\
0010\\
0001
\ end {array}\ derecha]\ izquierda [\ begin {array} {l}
x_ {1}\\
x_ {2}\\
x_ {3}\\
x_ {4}
\ end {array}\ derecha]. \ nonumber\]
Esta ecuación muestra cómo\(x\) se construye la palabra código a partir de los bits de información\((x_1,x_2,x_3,x_4)\). Llamamos a la matriz que define la construcción una matriz de codificador y la escribimos como\(H\):
\[x=H \Theta \nonumber \]
\[\mathrm{x}^{T}=\left(c_{1} c_{2} x_{1} c_{3} x_{2} x_{3} x_{4}\right) \quad \Theta^{T}=\left(x_{1} x_{2} x_{3} x_{4}\right) \nonumber \]
\ [H=\ left [\ begin {array} {c}
1101\\
1011\\
1000\\
0111\\
0100\\
0010\
0001
\ end {array}\ derecha]\ nonumber\]
Esto resume la construcción de un código Hamming\(x\).
Verifique para ver que el producto de la matriz de comprobación de paridad\(A^T\) y la matriz del codificador\(H\) es\(A^TH=0\). Interpreta este resultado.
Rellene la siguiente tabla para mostrar qué es el código Hamming (4,3):
| \(x_1\) | \(x_2\) | \(x_3\) | \(x_4\) | \(c_1\) | \(c_2\) | \(x_1\) | \(c_3\) | \(x_2\) | \(x_3\) | \(x_4\) |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | |||||||
| 0 | 0 | 1 | 1 | |||||||
| 0 | 1 | 0 | 0 | |||||||
| 0 | 1 | 0 | 1 | |||||||
| 0 | 1 | 1 | 0 | |||||||
| 0 | 1 | 1 | 1 | |||||||
| 1 | 0 | 0 | 0 | |||||||
| 1 | 0 | 0 | 1 | |||||||
| 1 | 0 | 1 | 0 | |||||||
| 1 | 0 | 1 | 1 | |||||||
| 1 | 1 | 0 | 0 | |||||||
| 1 | 1 | 0 | 1 | |||||||
| 1 | 1 | 1 | 0 | |||||||
| 1 | 1 | 1 | 1 |
Diseñe un\((11,n)\) código Hamming para codificar once bits de información contra errores únicos. Muestre sus ecuaciones\(c_{1}, c_{2}, \ldots, c_{n}\) y escriba la matriz del codificador\(H\) para\(x = H \Theta\)
Decodificación
Para decodificar un código de Hamming, formamos el síndrome\(A^Ty\) para la palabra clave recibida (y posiblemente errónea)\(\mathrm{y}=\mathrm{x} \oplus \mathrm{e}\). Porque\(A^Tx=0\), el síndrome es
\[\mathrm{s}=\mathrm{A}^{T} \mathrm{e} \nonumber \]
Convierte este número binario en su ubicación entera correspondiente y cambia el bit de\(y\) en esa ubicación. Si la ubicación es cero, no haga nada. Ahora quita los bits de información. Este es el algoritmo de decodificación.
Utilice la tabla de códigos Hamming (4,3) del Ejercicio 3 para construir una tabla de códigos recibidos que no contengan errores de bit o exactamente un error de bit. Aplicar el algoritmo de decodificación para construir\((x_1,x_2,x_3,x_4)\) y mostrar que todas las palabras de código recibidas con uno o menos errores se decodifican correctamente.
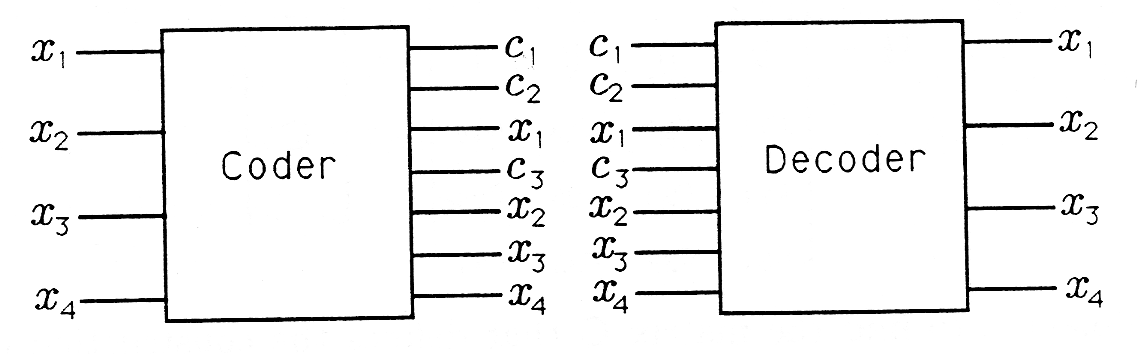
Hardware Digital
Las tablas que haya construido en los ejercicios 3 y 5 para codificar y decodificar códigos Hamming (4,3) pueden almacenarse en chips lógicos digitales. Su funcionalidad se ilustra en la Figura 1. El chip codificador acepta\((x_1,x_2,x_3,x_4)\) como su dirección y genera una palabra codificada. El chip decodificador acepta\((c_1c_2x_1c_3x_2x_3x_4)\) como su dirección y genera una palabra decodificada. En tus cursos de lógica digital estudiarás circuitos para implementar codificadores y decodificadores.
Discutir la posibilidad de detectar una palabra clave recibida (4,3) que no sea ni una palabra de código válida ni una palabra de código con un solo error. ¿Cómo usarías ese detector?
¿Qué fracción de palabras recibidas de siete bits se puede decodificar correctamente como códigos Hamming (4,3)?
Códigos sistemáticos
Los códigos Hamming sistemáticos son códigos cuyos bits de información conducen y cuyos bits de verificación siguen. El formato para un código (4,3) es entonces\((x_1x_2x_3x_4c_1c_2c_3)\). La construcción de una palabra de código (4,3) a partir de los bits de información puede escribirse como
\ [\ left [\ begin {array} {l}
x_ {1}\\
x_ {2}\\
x_ {3}\\
x_ {4}\\
c_ {1}\\
c_ {2}\\
c_ {3}
\ end {array}\ derecha] =\ left [\ begin {array} {cccc}
1 & 0 & 0 & 0\\
0 & amp; 1 & 0 & 0\\
0 & 0 & 1 & 0\\
0 & 0 & 0 & 0 & 1\\
c_ {11} & c_ {12} & c_ {13} & c_ {14}\\
c_ {21} & c_ {22} & c_ {23} & c_ {24}\\
c_ {31} & c_ {32} & c_ {33} & c_ {34}
\ end {array}\ derecha]\ left [\ begin {array} {c}
x_ {1}\\
x_ {2}\\
x_ {3}\\
x_ {4}
\ end {array}\ derecha]\ nonumber\]
La matriz del codificador toma la forma
\ [H=\ left [\ begin {array} {cccc}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 1 & 0\\
0 & 0 & 0 & 0 & 1\\
c_ {11} & c_ {12} & c_ {13} & c_ {14}\\
c_ {21} & c_ {22} & c_ { 23} & c_ {24}\\
c_ {31} & c_ {32} & c_ {33} & c_ {34}
\ end {array}\ right] =\ left [\ begin {array} {c}
I\\
c\
c
\ end {array}\ derecha]\ nonumber\]
El problema es encontrar la matriz\(C\) que define la construcción de bits de comprobación. La restricción\(A^Tx=0\) produce la restricción\(A^TH=0\) para que\(A^TH \Theta=0\). Las restricciones\(A^TH=0\) pueden escribirse como
\ [\ left\ {\ begin {array} {lllllll}
1 & 0 & 1 & 0 & 1 & 0 & 1\\
0 & 1 & 1 & 0 & 0 & 0 & 1 & 1\\
0 & 0 & 0 & 1 & 1 & 1 & 1
\ end {array}\ right\} =\ left [\ begin {array} {cccc}
1 & amp; 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 0 & 1 & 0\\
0 & 0 & 0 & 1\\
c_ {11} & c_ {12} & c_ {13} & c_ {14}\\
c_ {21} & c_ {22} & c_ {23} & c_ {24}\\
c_ {31} & ; c_ {32} & c_ {33} & c_ {34}
\ end {array}\ right] =\ left [\ begin {array} {llll}
0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 &
0 & 0 & 0 & 0
\ end {array}\ right]. \ nonumber\]
Estas restricciones producen todas las ecuaciones que necesitamos (doce ecuaciones en doce incógnitas) para determinar el\(c_{ij}\).
Resuelve la Ecuación 19 para el\(c_{ij}\). Mostrar que la matriz del codificador para un código Hamming sistemático (4,3) es
\ [H=\ left [\ begin {array} {llll}
1 & 0 & 0 & 0\\ 0 & 1 &
0 & 0\\ 0 &
0 & 1 & 0\\ 0 & 0 &
0 & 0 & 1\\ 0 & 1 & 1\\ 1 &
0 & 0 &
1 & 1\\ 1 & 1\\
1 & amp; 1 & 0 & 1
\ end {array}\ derecha]\ nonumber\]
Mostrar que la matriz del codificador del Ejercicio 7 es una permutación de la matriz del codificador en la Ecuación 14. (Es decir, las filas se reordenan.)
(MATLAB) Escribe un programa MATLAB que construya códigos Hamming (4,3) a partir de bits de información\((x_1x_2x_3x_4)\) y decodifica códigos Hamming (4,3)\((c_1c_2x_1c_3x_2x_3x_4)\) para obtener bits de información\((x_1x_2x_3x_4)\). Sintetice todos los códigos binarios de siete bits y muestre que su decodificador decodifica correctamente los códigos correctos y los códigos de error de un bit.


