1.1. Campos escalares
- Page ID
- 2968
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vector}[1]{\vec{\mathbf{#1}}}\)
\( \newcommand{\Disco}{\Bbb D}\)
\( \newcommand{\C}{\Bbb C}\)
\( \newcommand{\Q}{\Bbb Q}\)
\( \newcommand{\R}{\Bbb R}\)
\( \newcommand{\K}{\Bbb K}\)
\( \newcommand{\N}{\Bbb N}\)
\( \newcommand{\Z}{\Bbb Z}\)
\( \newcommand{\bo}{\textbf O}\)
\( \newcommand{\eps}{\varepsilon}\)
\( \newcommand{\la}{\lambda}\)
\( \newcommand{\om}{\omega}\)
\( \newcommand{\bmatriz}{\bmatrix \format \r&&\quad\r\\}\)
\( \newcommand{\bmatrize}{\bmatrix \format \c&&\quad\c\\}\)
\( \newcommand{\sep}{\, \equiv \,}\)
\( \newcommand{\xsep}{\quad \equiv \quad}\)
\( \newcommand{\xlsep}{\qquad \equiv \qquad}\)
\( \newcommand{\matriz}{\bmatrix\format\r&&\quad\r\\}\)
\( \newcommand{\endmatriz}{\endbmatrix}\)
\( \newcommand{\conj}[1]{\overline{}[1]}}\)
\( \newcommand{\vector}[1]{\vec{\textbf {}[1]}}}\)
\( \newcommand{\abs}[1]{\left\vert {#1} \right\vert}}\)
\( \newcommand{\norm}[1]{\left\Vert {#1}\right\Vert}\)
\( \newcommand{\bil}[2]{\left\langle {#1},{#2} \right\rangle}\)
\( \newcommand{\absbil}[2]{\abs{ \bil{#1}{#2} }}\)
\( \newcommand{\vectori}{\vector{\mathbf{\i}}}\)
\( \newcommand{\vectorj}{\vector{\mathbf{\j}}}\)
\( \newcommand{\vectork}{\vector{\mathbf{k}})\)
\( \newcommand{\vectorr}{\vector r}\)
\( \newcommand{\vectorrp}{\vector r}\,{}'}\)
\( \newcommand{\vectorrs}{\vector r}\,{}''}\)
\( \newcommand{\parteim}{\mathop{\text{Im}}\nolimits}\)
\( \newcommand{\partere}{\mathop{\text{Re}}\nolimits}\)
\( \newcommand{\sen}{\mathop{\text{sen}}\nolimits}\)
\( \newcommand{\sinc}{\mathop{\text{sinc}}\nolimits}\)
\( \newcommand{\sa}{\mathop{\text{sa}}\nolimits}\)
\( \newcommand{\senh}{\mathop{\text{senh}}\nolimits}\)
\( \newcommand{\arsenh}{\mathop{\text{arsenh}}\nolimits}\)
\( \newcommand{\arcosh}{\mathop{\text{arcosh}}\nolimits}\)
\( \newcommand{\Log}{\mathop{\text{Log}}\nolimits}\)
\( \newcommand{\Ln}{\mathop{\text{Ln}}\nolimits}\)
\( \newcommand{\Arg}{\mathop{\text{Arg}}\nolimits}\)
\( \newcommand{\arcsen}{\mathop{\text{arcsen}}\nolimits}\)
\( \newcommand{\arcos}{\mathop{\text{arccos}}\nolimits}\)
\( \newcommand{\arctg}{\mathop{\text{arctg}}\nolimits}\)
\( \newcommand{\ran}{\mathop{\text{ran}}\nolimits}\)
\( \newcommand{\maxe}{\mathop{\text{máx}}}\)
\( \newcommand{\mine}{\mathop{\text{mín}}}\)
\( \newcommand{\lime}{\mathop{\text{lím}}}\)
\( \newcommand{\lin}{\mathop{\text{lin}}\nolimits}\)
\( \newcommand{\inte}{\mathop{\text{int}}\nolimits}\)
\( \newcommand{\grad}{\mathop{\text{grad}}\nolimits}\)
\( \newcommand{\signo}{\mathop{\text{sig}}\nolimits}\)
\( \newcommand{\fl}{\mathop{\text{flot}}\nolimits}\)
\( \newcommand{\essup}{\mathop{\text{ess}\,\text{sup}}\nolimits}\)
\( \newcommand{\card}{\mathop{\text{card}}\nolimits}\)
\( \newcommand{\rot}{\mathop{\text{rot}}\nolimits}\)
\( \newcommand{\diver}{\mathop{\text{div}}\nolimits}\)
\( \newcommand{\volum}{\mathop{\text{vol}}\nolimits}\)
\( \newcommand{\Res}{\mathop{\text{Res}}\nolimits}\)
\( \newcommand{\grado}{\mathop{\text{gr}}\nolimits}\)
\( \newcommand{\dpar}[2]{\dfrac{\partial{#1}}{\partial{#2}}}\)
\( \newcommand{\dparx}[1]{\dfrac{\partial {#1}}{\partial x}}}\)
\( \newcommand{\dpary}[1]{\dfrac{\partial {#1}}{\partial y}}}\)
\( \newcommand{\dparz}[1]{\dfrac{\partial {#1}}{\partial z}}}\)
\( \newcommand{\dparr}[1]{\dfrac{\partial {#1}}{\partial r}}}\)
\( \newcommand{\dparth}[1]{\dfrac{\partial {#1}}{\partial \theta}}}\)
\( \newcommand{\dparxx}[1]{\dfrac{\partial^2 {#1}}{\partial x^2}}}\)
\( \newcommand{\dparyy}[1]{\dfrac{\partial^2 {#1}}{\partial y^2}}}\)
\( \newcommand{\dparxy}[1]{\dfrac{\partial^2 {#1}}{\partial x \partial y}}}\)
\( \newcommand{\dparzz}[1]{\dfrac{\partial^2 {#1}}{\partial z^2}}}\)
\( \newcommand{\dparxz}[1]{\dfrac{\partial^2 {#1}}{\partial x \partial z}}}\)
\( \newcommand{\dparyz}[1]{\dfrac{\partial^2 {#1}}{\partial y \partial z}}}\)
\( \newcommand{\dpardos}[2]{\dfrac{\partial^2 {#1}}{\partial {#2}^2}}}\)
\( \newcommand{\dparcruz}[3]{\dfrac{\partial^2 {#1}}{\partial {#2} \partial {#3}}}\)
\( \newcommand{\dtan}[1]{ \dfrac{\partial {#1}}{\partial {\vector t}} }}\)
\( \newcommand{\dnormal}[1]{ \dfrac{\partial {#1}}{\partial {\vector n}} }}\)
Introducción
Los campos escalares son funciones que dependen de dos o más variables cuyos valores son números reales. Los campos vectoriales son funciones que dependen de dos o más variables y cuyos valores son vectores; veamos algunos ejemplos simples.
- La función \(a(x,y)=xy\) es el campo escalar de dos variables que nos proporciona el área del rectángulo de lados \(x\) e \(y\).
- La función \( r(x,y) = \Vert (x,y)\Vert=\sqrt{x^2+y^2} \) es el campo escalar de dos variables que expresa la distancia desde el punto \((x,y)\) hasta el origen de coordenadas o, en otras palabras, el radio polar \( r \) del punto \( (x,y) \).
- La función \(\rho(x,y,z)=\Vert(x,y,z)\Vert=\sqrt{x^2+y^2+z^2}\) es el campo escalar de tres variables que expresa la distancia desde el punto \((x,y,z)\) hasta el origen de coordenadas. (Con objeto de no generar confusión con las notaciones habituales para las coordenadas cilíndricas y esféricas que estudiaremos más adelante, mantendremos la diferencia entre la notación \( r \) en 2D y \( \rho \) en 3D para la distancia de un punto al origen).
- La función \(\vecs r(x,y,z)=x\,\vecs i+y\,\vecs j+z\,\vecs k\) es el campo vectorial que a cada punto \((x,y,z)\) le asigna su vector de posición. En particular, el campo \( \rho(x,y,z) \) del ejemplo anterior es el módulo (o norma) de \(\vecs r(x,y,z)\), es decir, \(\rho(x,y,z)=\Vert{\vecs r(x,y,z)}\Vert\).
- Sea \(\vecs u(x,y,z)=\vecs r(x,y,z)\big/\Vert{\vecs r(x,y,z)}\Vert\) el vector unitario de la misma dirección y sentido que el vector de posición \(\vecs r(x,y,z)\), la función \[ \vecs F(x,y,z) =-G Mm\dfrac{\vecs r(x,y,z)}{\Vert{\vecs r(x,y,z)}\Vert^3}=-G Mm\dfrac{\vecs u(x,y,z)}{\Vert{\vecs r(x,y,z)}\Vert^2} =-G Mm\dfrac{\vecs u(x,y,z)}{\rho^2(x,y,z)} \notag \] es el campo vectorial que expresa la fuerza de atracción que ejerce la Tierra sobre un cuerpo de masa \(m\) situado en el punto \((x,y,z)\), siendo \(M\) la masa de la Tierra (en cuyo centro se sitúa el origen de coordenadas) y \(G\) la constante de gravitación universal de Newton.
En las aplicaciones a la geometría, la física y otras ciencias, los campos escalares son funciones que representan valores de magnitudes escalares como la longitud, el área, el volumen, la densidad, la masa, la energía o el trabajo desarrollado por una fuerza. Los campos vectoriales son funciones que representan magnitudes vectoriales como la posición, la velocidad, la aceleración o la fuerza.
Campos escalares
Un campo escalar de dos variables es una función \( f \) que asigna a cada punto \((x,y)\) de un conjunto \(U\) del plano \(\R^2\) un número real \(f(x,y)\), lo que se suele indicar como \(f \colon (x,y) \in U \to f(x,y) \in \R\). El conjunto \(U\) se llama dominio de definición de \(f\).
Un campo escalar de tres variables es una función \(f\) que asigna a cada punto \((x,y,z)\) de su dominio de definición \(U\) en el espacio tridimensional \(\R^3\) un número real \(f(x,y,z)\), lo que se suele indicar como \(f \colon (x,y,z) \in U \to f(x,y, z) \in \R\).
Algunas observaciones sobre la notación. (1) En ocasiones los campos escalares vienen dados en función de la posición, por lo que a veces se usa una notación vectorial en la que se identifica un punto con su vector de posición \(\vecs r=(x,y)=x\, \vecs i+y\,\vecs j\) (o bien \(\vecs r=(x,y,z)= x\, \vecs i+y\, \vecs j + z\, \vecs k\) en el caso tridimensional) y los campos escalares son funciones que asignan a cada \(\vecs r\) un valor real \(f(\vecs r)\).
(2) Es habitual escribir los vectores en columna, \(\vecs r=\left[ \begin{matrix} x \\ y \end{matrix} \right] \). Sin embargo, mientras no haya posibilidad de confusión, mantendremos por comodidad la notación como vectores-fila. Así, para indicar el valor de un campo escalar \(f\) en un punto \(A=\vecs r=\left[ \begin{matrix} x \\ y \end{matrix} \right] \), escribiremos \(f(A)\), \(f(\vecs r)\) o \(f(x,y)\), pero no \(f \left( \left[ \begin{matrix} x \\ y \end{matrix} \right] \right) \). No obstante, en algunos casos especiales sí será importante distinguir entre vectores-fila y vectores-columna, lo que se indicará oportunamente.
(3) En general, usaremos los campos de dos variables para justificar las definiciones y obtener interpretaciones geométricas que se pueden visualizar solo con dos variables, pero enunciaremos los principales resultados para campos de tres variables, que es el contexto natural de aplicación de los resultados. Por tanto, casi todo lo que digamos valdrá para campos de dos variables, sin más que suprimir la tercera coordenada o la variable \(z\), y puede extenderse de manera natural a campos que dependen de cuatro o más variables
\[ f \colon (x_1, x_2, \ldots, x_n) \in U \subset \R^n \to f(x_1, x_2, \ldots, x_n) \in \R. \notag \]
Por descontado, cuando exista alguna diferencia notable entre los casos 2D y 3D, (por ejemplo, en la noción de rotacional), la especificaremos con detalle.
Polinomios
Los campos escalares más simples son los polinomios. Un monomio de dos variables \(x\) e \(y\) es un producto de la forma \(a x^m y^n\), donde \(m\) y \(n\) son números enteros no negativos y \(a\) es un coeficiente escalar; el grado del monomio es la suma \(m+n\) de los exponentes de las variables. Por ejemplo, el área de un rectángulo \(a(x,y)=xy\) es un monomio de grado 2 con dos variables. Si tenemos un cilindro circular recto de altura \(h\) y radio de la base \(r\), su volumen \(v(r,h)=\pi r^2h\) es un monomio de grado 3 con dos variables.
Para tres variables, un monomio es un producto de la forma \(a x^m y^n z^p\); el grado del monomio es la suma \(m+n+p\) de los exponentes de las variables. El volumen \(v(x,y,z)=xyz\) de un ortoedro de lados \(x,y,z\), es un monomio de grado 3 con tres variables.
Un polinomio es una suma de monomios y el grado del polinomio es el mayor de los grados de los monomios que lo componen; veamos algunos ejemplos.
- Los polinomios de grado \(0\) son las funciones constantes.
- El campo escalar \(f(x,y)=ax+by \) es un polinomio de grado \(1 \). Si usamos \(\vecs r=x\,\vecs i+y\,\vecs j \) y tomamos el vector constante \(\vecs c =a\,\vecs i+b\,\vecs j \), entonces \(f \) se puede representar mediante el producto escalar \(f(\vecs r)=\vecs c \cdot \vecs r \), de manera que, con la terminología del álgebra lineal, \(f \) es la transformación lineal de \(\R^2 \) en \( \R \) generada por el vector \( \vecs c \) entendido como una matriz fila (análogamente en dimensión \(3 \)).
- El campo \(f(x,y)=ax^2+bxy+cx^2 \) es un polinomio de grado \(2 \) que podemos escribir \[ f(x,y)=[x \quad y] \left[ \begin{matrix} a & b/2 \\ b/2 & c \end{matrix} \right] \left[ \begin{matrix} x \\ y \end{matrix} \right] \notag \] que, de nuevo en el lenguaje del álgebra lineal, es la forma cuadrática generada por la matriz simétrica \( {\bf A}=\left[\begin{matrix} a & b/2 \\ b/2 & c \end{matrix}\right] \) y que se puede escribir como \(f(\vecs r)={\vecs r}\,{}^T {\bf A} \vecs r= \vecs r \cdot {\bf A} \vecs r \).
- Análogamente, la forma cuadrática \( f(\vecs r)={\vecs r}\,{}^T {\bf A} \vecs r= \vecs r \cdot {\bf A} \vecs r \) generada en \(\R^3\) por una matriz simétrica \( {\bf A} \) de dimensión \( 3 \) es un polinomio de grado 2 en tres variables. Por ejemplo, la función \(\rho^2(x,y,z)={x^2+y^2+z^2} \), que proporciona el cuadrado de la distancia desde el punto \((x,y,z) \) hasta el origen de coordenadas, es un polinomio de grado 2 con tres variables que es la forma cuadrática generada en \(\R^3 \) por la matriz identidad. Será necesario tener un buen conocimiento de las formas cuadráticas para abordar la caracterización de los puntos críticos de un campo escalar que veremos más adelante.
- El campo \( f(x,y)=3x^3y^2-xy^4+3xy-2 \) es un polinomio de grado 5 en dos variables.
- El campo \(f(x,y,z)=x^2yz^3+z^2y-3xy-z+2 \) es un polinomio de grado 6 en tres variables.
Campos escalares centrales
Se dice que un campo escalar es un campo central (o radial, en algunos textos) cuando su valor en un punto depende únicamente de la distancia del punto a un punto fijo de antemano llamado centro o (también, en algunos textos, fuente o sumidero). Habitualmente, el centro es el origen de coordenadas, en cuyo caso la distancia desde un punto \( (x,y,z) \) al centro es \( \rho(x,y,z)=\Vert(x,y,z)\Vert=\sqrt{x^2+y^2+z^2} \), y los campos centrales en \(\R^3\) se escriben \(f(x,y,z)=\psi\left(\rho(x,y,z) \right) \), donde \(\psi(t)\) es una función de clase \( C^1 \) en un intervalo del semieje \( t \geq 0 \). Para el caso 2D, basta con suprimir \( z\), o sea, \( f(x,y) = \psi\left(\Vert(x,y)\Vert\right)=\psi(r) \) con \( r=\sqrt{x^2+y^2} \).
Límites y continuidad de un campo escalar
Observaciones. (1) Como en el caso de los campos centrales, casi todos los campos que aparecen en la práctica se obtienen aplicando a un polinomio en varias variables las operaciones habituales -suma, resta, multiplicación y división- y las funciones elementales de una variable (potencias, raíces, exponenciales, logaritmos, funciones trigonométricas y sus inversas, valor absoluto, etc.). A veces se trabaja también con funciones que proporcionan el máximo o mínimo de un conjunto finito de valores \( f(x,y)=\maxe\{|x|, |y|\} \), por ejemplo). En estos casos tenemos, como regla general, que si un campo escalar de varias variables viene dado por una o varias fórmulas, entonces su dominio es el conjunto más grande en el que dichas fórmulas tienen sentido. Veamos algunos ejemplos:
- Los polinomios están definidos en todo \( \R^2\) o \( \R^3 \) según sean de dos o de tres variables.
- El dominio del campo \( f(x,y)=\sqrt{1-x^2-y^2} \) está formado por los puntos \( (x,y) \) del plano que cumplen \( x^2+y^2 \leq 1 \), es decir \( U \) es el círculo de centro el origen y radio 1 o círculo unidad.
- El dominio de la función \( f(x,y) = \log(1+x-y) \) está formado por los puntos \( (x,y) \) del plano tales que \( 1+x-y>0\), es decir, es un semiplano.
- El campo \( f(x,y,z) = \sqrt{1-x^2-y^2-z^2} \) está definida para los puntos \( (x,y,z) \) tales que \( x^2+y^2+z^2 \leq 1 \), es decir, su dominio es la esfera unidad de \( \R^3 \).
- La función \( f(x,y,z) = (x^2+y^2+z^2)^{-1} \) está definida para los puntos \( (x,y,z)\neq (0,0,0)\), es decir, su dominio es todo \( \R^3 \) salvo el origen.
(2) La noción de límite es el concepto esencial sobre el que se construye el cálculo de funciones de una variable. El límite de un campo escalar de varias variables es una extensión directa de dicho concepto; en principio, bastaría con sustituir el valor absoluto, que nos da la distancia entre puntos de la recta real, por la norma euclídea que nos da la distancia entre puntos del plano o del espacio. Sin embargo, hay una diferencia notable entre los casos de una y varias variables: en el caso de una variable solamente nos podemos acercar al punto por la izquierda o por la derecha, mientras que en el caso de varias variables nos podemos acercar al punto desde muchas direcciones, por eso, como paso previo a la definición formal de límite de un campo escalar de varias variables, es necesario distinguir algunas situaciones geométricas especiales.
Puntos interiores y puntos de la frontera. Empezando por el caso bidimensional, diremos que \( A \) es un punto interior de un conjunto \( U \subset \R^2 \) si hay un círculo centrado en \( A \) que se queda totalmente contenido en \( U \). Diremos que \( B \) es un punto de la frontera de \( U \) si en todo círculo centrado en \( B \) hay puntos que están en \( U \) y puntos que no están en \( U \).
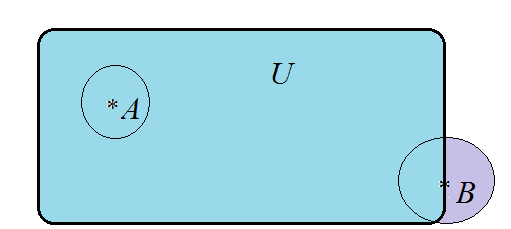
El punto \(A\) es un punto interior de \( U \), el punto \( B \) está en la frontera de \( U \).
Estos conceptos se trasladan al espacio tridimensional cambiando "círculo'' por "esfera''. Cuando \( U \) es el dominio de definición de un campo escalar, la diferencia esencial es que en un punto interior de \( U \) el campo está definido en todo el espacio que lo que rodea y podemos acercarnos a él desde todas las direcciones posibles, mientras que cerca de un punto de la frontera siempre hay una zona del espacio en la que el campo no está definido.
En la gran mayoría de los casos el dominio \( U \) viene definido como el conjunto de puntos que cumplen una o varias igualdades o desigualdades. En este caso la frontera de \( U \) está formada por los puntos donde se cumple alguna igualdad y sus puntos interiores son los puntos (si hay) donde se cumplen todas las desigualdades estrictamente. Por ejemplo, el círculo unidad está formado por los puntos \( (x,y) \) del plano que cumplen \( x^2+y^2 \leq 1 \). Su frontera es la circunferencia unidad \( x^2+y^2=1\) (los puntos donde se da la igualdad), mientras que sus puntos interiores son los puntos \( (x,y) \) tales que \( x^2+y^2 < 1 \) (los puntos donde se da la desigualdad estricta).
Al igual que en este caso, en la mayoría de los casos de interés (rectángulos, círculos, triángulos, semiplanos, esferas, cilindros, conos, cubos, ortoedros, etc.) la frontera coincide con lo que nos dice la intuición geométrica, por lo que no profundizaremos más en estos conceptos.
Límite y continuidad de un campo escalar. Sea \(U\) el dominio de definición (en 2D o 3D) de un campo \(f \). Sea \(A\) un punto interior de \( U \) o bien un punto de la frontera de \( U \) al que nos podemos acercar tanto como queramos por puntos \( X \) de \( U \) distintos de él. Diremos que \( L \) es el límite de \( f(X) \) cuando
\( X \) tiende a \( A\), lo que escribimos \(\displaystyle \lime_{X \to A} f(X)=L\), cuando los valores de \( f(X) \) están tan cercanos a \( L \) como queramos en todos los puntos \( X\in U \) lo suficientemente cerca de \( A \) pero con \( X \ne A \).
Diremos que \( f \) es continuo en \( A\) cuando \( \displaystyle \lime_{X \to A} f(X)=f(A) \) y se dice que \( f \) es un campo escalar continuo cuando es continuo en todos los puntos de su dominio de definición.
Puede probarse que las propiedades algebraicas de los límites de campos de varias variables (suma, producto, composición, etc.) son similares a las de los límites de funciones de una variable y, por tanto, lo mismo ocurre con la continuidad. La comprobación teórica de estas propiedades, así como un estudio exhaustivo de la existencia de límites, límites laterales, límites direccionales, etc., basado en la definición formal \( \epsilon-\delta \) se aleja de los objetivos de este curso. Lo importante aquí es que, en particular, los polinomios son funciones continuas y la composición de funciones continuas es continua, de forma que (casi) todas las funciones que se utilizan en la práctica son continuas.
Ejercicios
Ejercicio 1. Para cada uno de los siguientes campos escalares, determina su dominio de definición y la frontera de dicho dominio.
\[ \begin{array}{rlrl} (1) & f(x,y)=3x^2y-x^2+y & {}\quad(2) & f(x,y)=\sqrt{x^2+y^2-16} \\ (3) & f(x,y)=y/x& {}\quad(4) & f(x,y)=\sqrt{(9-x^2-y^2)(x^2+y^2-1)} \\ (5) & f(x,y)={2x}/(x^2-y^2) & {}\quad(6) & f(x,y)=\text{el ángulo polar de \( (x,y) \)}\\ (7) & f(x,y,z)=\log(4-x+2y+z) & {}\quad(8) & f(x,y,z)=4y-z\sqrt{x^2z} \end{array} \notag \]
Ejercicio 2. Sean \( r=\Vert(x,y)\Vert=\sqrt{x^2+y^2}\) y \( \rho=\Vert(x,y,z)\Vert=\sqrt{x^2+y^2+z^2}\) la distancia, respectivamente en 2D y 3D, desde un punto al origen. Halla el dominio de los campos centrales \(r^n\) y \(\rho^n\) (para \( n=\pm1,\pm2,\ldots \) ), \( \log(r) \) y \( \log(\rho) \), donde \(\log\) indica la función logaritmo neperiano.
*Ejercicio 3. El campo escalar definido por \[f(x,y)=\begin{cases} \dfrac{xy}{x^2+y^2} & \text{si $(x,y)\neq (0,0)$},\\ 0 & \text{si $(x,y)=(0,0)$;}\end{cases} \notag\] es un ejemplo de un campo escalar no continuo en el origen. Para comprobarlo, calcula el límite del campo escalar cuando \( (x,y) \) se acerca al origen siguiendo la dirección de una línea recta de la forma \(y=mx\) y comprueba que el valor del límite depende de la inclinación \(m\).
*Ejercicio 4. Considera el campo escalar \( f \) dado por
\[ f(x,y)=\begin{cases}\dfrac{2x^2y}{x^2+y^2} & \text{si }(x,y)\neq (0,0),\\
0 & \text{si }(x,y)=(0,0).\end{cases}\notag\]
Aunque se parece al del ejercicio anterior, esta campo sí es continuo en el origen. Para comprobar este hecho, prueba que \( |2xy| \leq x^2+y^2 \) (desarrollando la desigualdad \( (x-y)^2\geq 0) \) y utiliza esto para acotar \( f \) superiormente y deducir que \( \displaystyle \lime_{(x,y)\to (0,0)} f(x,y)=0 = f(0,0) \).

