1.2. Gráfica de un campo escalar
- Page ID
- 2976
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vector}[1]{\vec{\mathbf{#1}}}\)
\( \newcommand{\Disco}{\Bbb D}\)
\( \newcommand{\C}{\Bbb C}\)
\( \newcommand{\Q}{\Bbb Q}\)
\( \newcommand{\R}{\Bbb R}\)
\( \newcommand{\K}{\Bbb K}\)
\( \newcommand{\N}{\Bbb N}\)
\( \newcommand{\Z}{\Bbb Z}\)
\( \newcommand{\bo}{\textbf O}\)
\( \newcommand{\eps}{\varepsilon}\)
\( \newcommand{\la}{\lambda}\)
\( \newcommand{\om}{\omega}\)
\( \newcommand{\bmatriz}{\bmatrix \format \r&&\quad\r\\}\)
\( \newcommand{\bmatrize}{\bmatrix \format \c&&\quad\c\\}\)
\( \newcommand{\sep}{\, \equiv \,}\)
\( \newcommand{\xsep}{\quad \equiv \quad}\)
\( \newcommand{\xlsep}{\qquad \equiv \qquad}\)
\( \newcommand{\matriz}{\bmatrix\format\r&&\quad\r\\}\)
\( \newcommand{\endmatriz}{\endbmatrix}\)
\( \newcommand{\conj}[1]{\overline{}[1]}}\)
\( \newcommand{\vector}[1]{\vec{\textbf {}[1]}}}\)
\( \newcommand{\abs}[1]{\left\vert {#1} \right\vert}}\)
\( \newcommand{\norm}[1]{\left\Vert {#1}\right\Vert}\)
\( \newcommand{\bil}[2]{\left\langle {#1},{#2} \right\rangle}\)
\( \newcommand{\absbil}[2]{\abs{ \bil{#1}{#2} }}\)
\( \newcommand{\vectori}{\vector{\mathbf{\i}}}\)
\( \newcommand{\vectorj}{\vector{\mathbf{\j}}}\)
\( \newcommand{\vectork}{\vector{\mathbf{k}})\)
\( \newcommand{\vectorr}{\vector r}\)
\( \newcommand{\vectorrp}{\vector r}\,{}'}\)
\( \newcommand{\vectorrs}{\vector r}\,{}''}\)
\( \newcommand{\parteim}{\mathop{\text{Im}}\nolimits}\)
\( \newcommand{\partere}{\mathop{\text{Re}}\nolimits}\)
\( \newcommand{\sen}{\mathop{\text{sen}}\nolimits}\)
\( \newcommand{\sinc}{\mathop{\text{sinc}}\nolimits}\)
\( \newcommand{\sa}{\mathop{\text{sa}}\nolimits}\)
\( \newcommand{\senh}{\mathop{\text{senh}}\nolimits}\)
\( \newcommand{\arsenh}{\mathop{\text{arsenh}}\nolimits}\)
\( \newcommand{\arcosh}{\mathop{\text{arcosh}}\nolimits}\)
\( \newcommand{\Log}{\mathop{\text{Log}}\nolimits}\)
\( \newcommand{\Ln}{\mathop{\text{Ln}}\nolimits}\)
\( \newcommand{\Arg}{\mathop{\text{Arg}}\nolimits}\)
\( \newcommand{\arcsen}{\mathop{\text{arcsen}}\nolimits}\)
\( \newcommand{\arcos}{\mathop{\text{arccos}}\nolimits}\)
\( \newcommand{\arctg}{\mathop{\text{arctg}}\nolimits}\)
\( \newcommand{\ran}{\mathop{\text{ran}}\nolimits}\)
\( \newcommand{\maxe}{\mathop{\text{máx}}}\)
\( \newcommand{\mine}{\mathop{\text{mín}}}\)
\( \newcommand{\lime}{\mathop{\text{lím}}}\)
\( \newcommand{\lin}{\mathop{\text{lin}}\nolimits}\)
\( \newcommand{\inte}{\mathop{\text{int}}\nolimits}\)
\( \newcommand{\grad}{\mathop{\text{grad}}\nolimits}\)
\( \newcommand{\signo}{\mathop{\text{sig}}\nolimits}\)
\( \newcommand{\fl}{\mathop{\text{flot}}\nolimits}\)
\( \newcommand{\essup}{\mathop{\text{ess}\,\text{sup}}\nolimits}\)
\( \newcommand{\card}{\mathop{\text{card}}\nolimits}\)
\( \newcommand{\rot}{\mathop{\text{rot}}\nolimits}\)
\( \newcommand{\diver}{\mathop{\text{div}}\nolimits}\)
\( \newcommand{\volum}{\mathop{\text{vol}}\nolimits}\)
\( \newcommand{\Res}{\mathop{\text{Res}}\nolimits}\)
\( \newcommand{\grado}{\mathop{\text{gr}}\nolimits}\)
\( \newcommand{\dpar}[2]{\dfrac{\partial{#1}}{\partial{#2}}}\)
\( \newcommand{\dparx}[1]{\dfrac{\partial {#1}}{\partial x}}}\)
\( \newcommand{\dpary}[1]{\dfrac{\partial {#1}}{\partial y}}}\)
\( \newcommand{\dparz}[1]{\dfrac{\partial {#1}}{\partial z}}}\)
\( \newcommand{\dparr}[1]{\dfrac{\partial {#1}}{\partial r}}}\)
\( \newcommand{\dparth}[1]{\dfrac{\partial {#1}}{\partial \theta}}}\)
\( \newcommand{\dparxx}[1]{\dfrac{\partial^2 {#1}}{\partial x^2}}}\)
\( \newcommand{\dparyy}[1]{\dfrac{\partial^2 {#1}}{\partial y^2}}}\)
\( \newcommand{\dparxy}[1]{\dfrac{\partial^2 {#1}}{\partial x \partial y}}}\)
\( \newcommand{\dparzz}[1]{\dfrac{\partial^2 {#1}}{\partial z^2}}}\)
\( \newcommand{\dparxz}[1]{\dfrac{\partial^2 {#1}}{\partial x \partial z}}}\)
\( \newcommand{\dparyz}[1]{\dfrac{\partial^2 {#1}}{\partial y \partial z}}}\)
\( \newcommand{\dpardos}[2]{\dfrac{\partial^2 {#1}}{\partial {#2}^2}}}\)
\( \newcommand{\dparcruz}[3]{\dfrac{\partial^2 {#1}}{\partial {#2} \partial {#3}}}\)
\( \newcommand{\dtan}[1]{ \dfrac{\partial {#1}}{\partial {\vector t}} }}\)
\( \newcommand{\dnormal}[1]{ \dfrac{\partial {#1}}{\partial {\vector n}} }}\)
Gráfica de un campo escalar
Como ya sabes, la gráfica es una herramienta esencial para estudiar las funciones de una variable y visualizar su comportamiento. Para campos escalares de dos variables también se da esta conexión entre las propiedades algebraicas de las fórmulas que los definen y las propiedades geométricas de sus gráficas, que son superficies en el espacio.
La gráfica de un campo escalar de dos variables continuo \( f\colon U \to \R \) es el conjunto del espacio tridimensional \( \R^3 \) dado por \( \left\{ \bigl(x,y, f(x,y) \bigr) \in \R^3 \colon (x,y)\in U \right\}\).
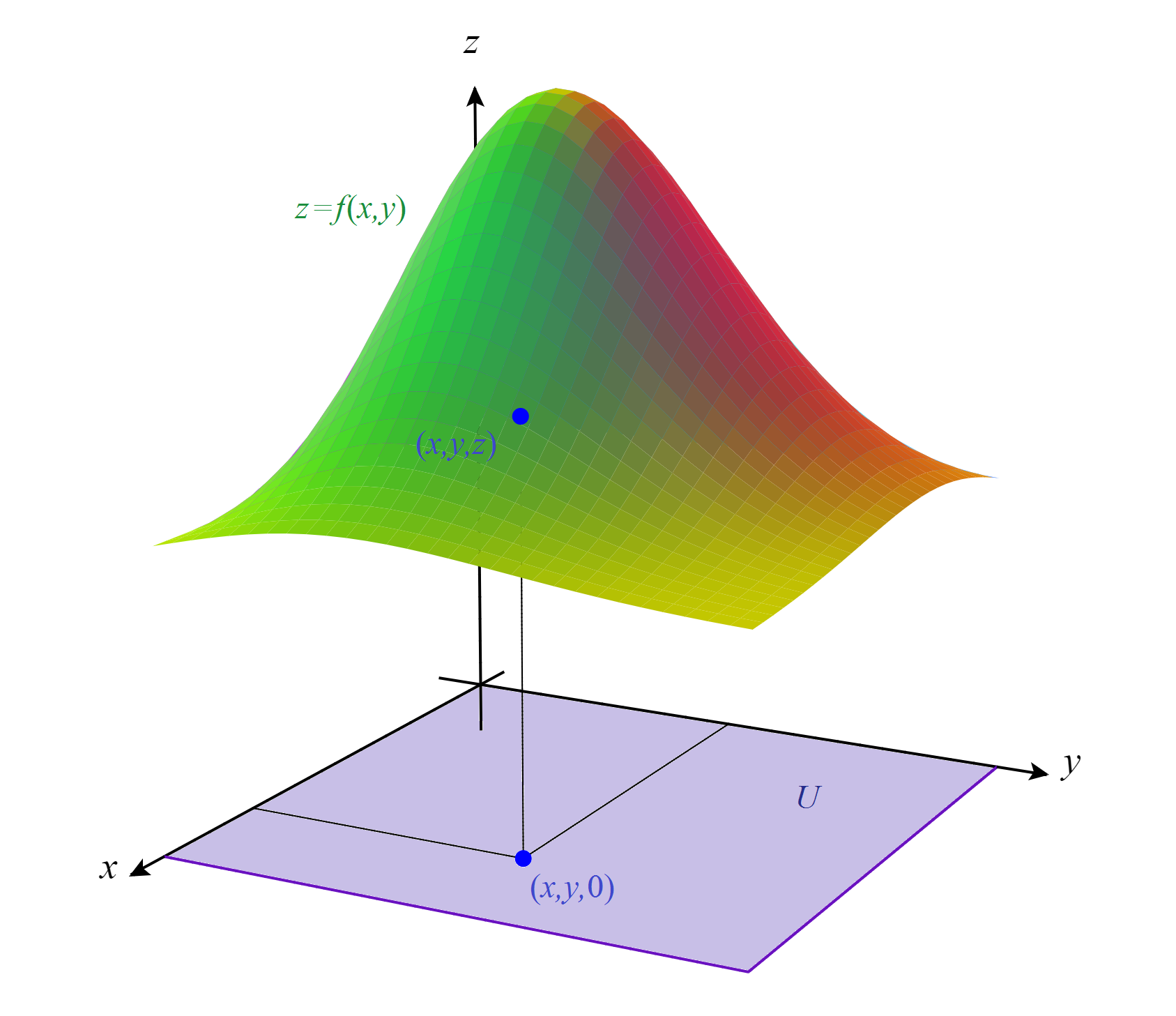
Superficie de ecuación \( z=f(x,y) \).
Este conjunto puede visualizarse como una superficie en \( \R^3 \) que se llama superficie de ecuación \( z=f(x,y) \) porque se construye de la siguiente manera: se coloca el dominio \( U \) en el plano del suelo y, situado sobre la vertical de cada punto \( (x,y) \in U \), el punto de correspondiente en la gráfica de \( f\) es \( \bigl(x,y, f(x,y) \bigr) \) cuya tercera coordenada es \( z=f(x,y) \). No es nada fácil dibujar a mano alzada la gráfica de un campo escalar de dos variables con la salvedad, quizás, de los planos y algunas cuádricas. La versión en español de la aplicación CalcPlot3D es una magnífica herramienta para dibujar superficies del tipo \( z=f(x,y) \) (y muchas cosas más que iremos viendo) introducidas desde el teclado.
Gráfica de un campo central. Si \( f(x,y)=\psi(r) \), con \( a\leq r=\sqrt{x^2+y^2} = \Vert (x,y)\Vert \leq b \) es un campo central, su gráfica es una superficie de revolución que se obtiene haciendo girar la gráfica \( C \) de la función \( z=\psi(x) \) en el plano \( XZ \) (o la de \( z=\psi(y) \) en el plano \( YZ \)) alrededor del eje \( Z \). Estudiaremos con más detenimiento las superficies de revolución en el Capítulo ??.
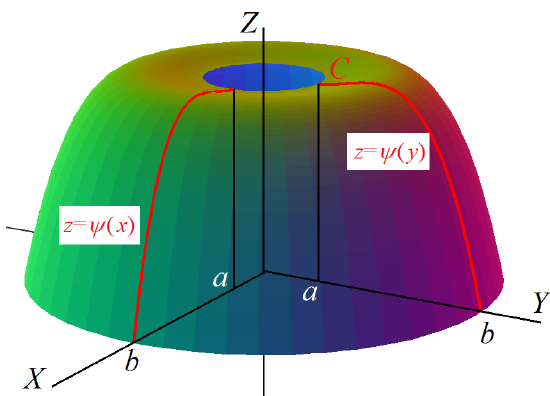
Superficie de revolución alrededor del eje \( Z \).
Curvas de nivel
Una forma alternativa de visualizar cómo es un campo escalar de dos variables es estudiar sus curvas de nivel, que son las curvas definidas en el plano \( XY \) por la ecuación \( f(x,y)=c \) para cada número \( c \in \R \). Este número \( c \) representa el nivel, de manera que el valor del campo \( f(x,y) \) en todos los puntos de la curva de nivel es el mismo \( c \). Geométricamente, la curva de nivel \( (x,y)=c \) se obtiene proyectando sobre el plano \( XY \) la curva intersección de la superficie \( z=f(x,y) \) con el plano horizontal de ecuación \( z=c \).
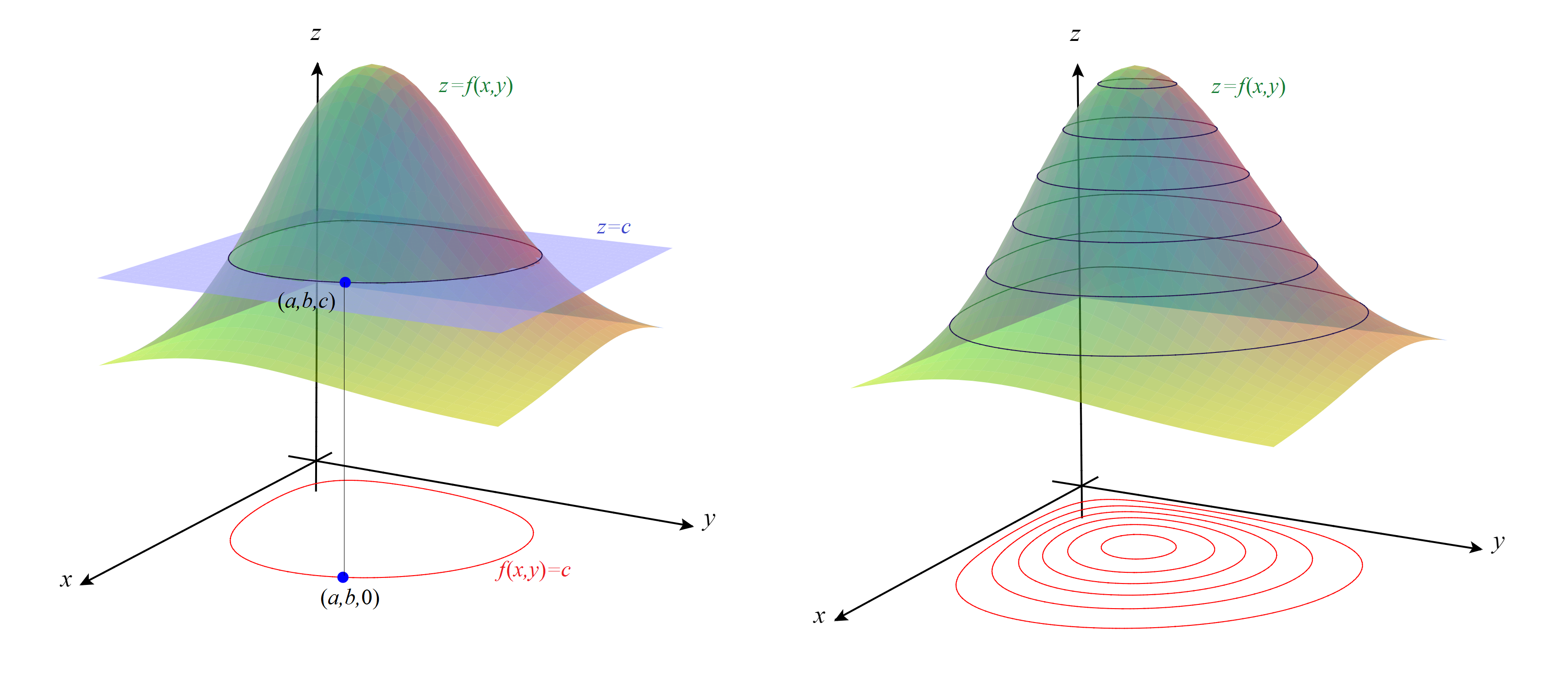
Curva de nivel por un punto. Curvas de nivel.
Ejemplos típicos de curvas de nivel son los mapas topográficos, donde una curva de nivel indica los puntos del terreno que están a una misma altura; los mapas meteorológicos de presión, donde las curvas de nivel, las isobaras, indican los puntos de la superficie sobre los que la presión es la misma; o los mapas meteorológicos de temperatura, donde las curvas de nivel, las isotermas, indican los puntos de la superficie sobre los que la temperatura es la misma. La aplicación CalcPlot3D permite dibujar las curvas de nivel de campos \( f(x,y) \) definidas desde el teclado.
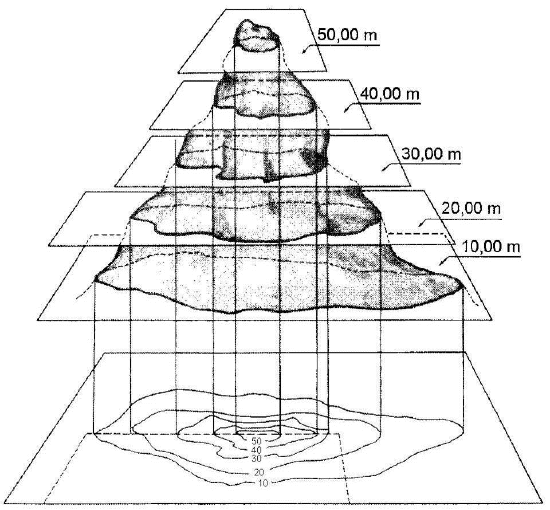
Curvas de nivel para \(c=10, 20, \ldots, 50\) metros.
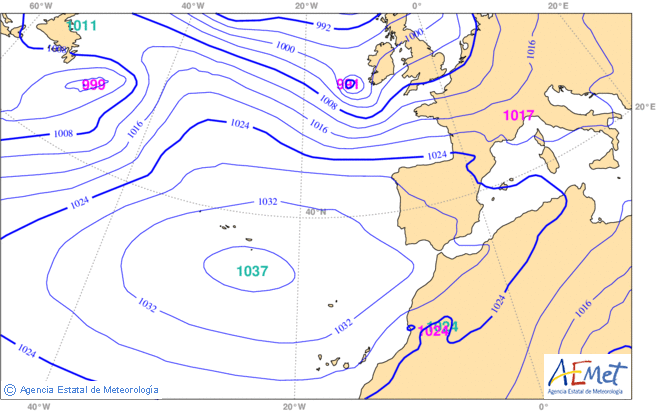
Isobaras.
En los dos dibujos anteriores el valor del nivel de cada curva viene escrito sobre la curva. También es común utilizar, en vez de números, una graduación de colores para indicar la subida o bajada de los niveles, como en el mapa de isotermas que se muestra a continuación, lo que nos permite estimar el valor del campo en un punto \( (x,y) \) y analizar cómo crecen o decrecen los valores del campo.
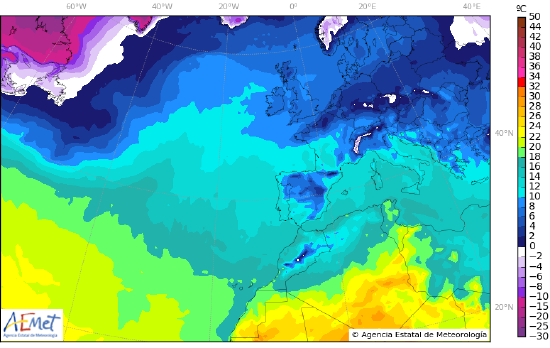
Isotermas.
Hay otro tipo de información que se puede obtener, por ejemplo, en las zonas en las que las curvas están muy juntas, es decir, los intervalos entre niveles son estrechos, la superficie tiene una inclinación acentuada, mientras que en las zonas en las que las curvas de nivel están muy separadas lo que ocurre es que la superficie tiene poca inclinación.
Las curvas de nivel de un campo central en el plano \( f(x,y)=\psi\bigl(\Vert(x,y)\Vert\bigr)\) son circunferencias centradas en el origen y viceversa: si las curvas de nivel de un campo son circunferencias centradas en el origen, entonces el campo es central. Por ello se suele decir que los campos centrales en el plano tienen simetría circular.
Superficies de nivel. No es posible visualizar las superficies definidas por campos de tres variables, digamos \( w=f(x,y,z) \), porque son conjuntos de \( \R^4 \). En este caso, tenemos como alternativa estudiar sus superficies de nivel, que son las superficies definidas en el espacio por la ecuación \( f(x,y,z)=c \) para cada número \( c \in \R \). Por ejemplo, las superficies de nivel de un campo central \( f(x,y,z)=\psi\bigl( \Vert (x,y,z)\Vert \bigr) \) son esferas centradas en el origen y viceversa: si las superficies de nivel de un campo son esferas centradas en el origen, entonces el campo es central. Por ello se suele decir que los campos centrales en el espacio tienen simetría esférica.
Ejercicios
Ejercicio 1. Utiliza la aplicación CalcPlot3D para dibujar las gráficas de los campos que se dan a continuación y sus curvas de nivel.
\[\begin{array}{rlrlrl}
(1) & f(x,y)=\cos(\pi x) + \sen(\pi y) & {}\quad
(2) & f(x,y)=xy &{}\quad
(3) & f(x,y)=5-x^3+xy \\
(4) & f(x,y)=x^2+2xy+3y^2 &{}\quad
(5) & f(x,y)= e^{-(x^2+y^2)/3} &{}\quad
(6) & f(x,y)=\sqrt{x^2+1+y^2} \\
(7) & f(x,y)= (3x+y)\cos(\pi xy) &{}\quad
(8) & f(x,y)= \sqrt{64-x^2} &{}\quad
(9) & f(x,y)= e^{-x} (2y^2-x^2) \\
(10) & f(x,y)=7xy/e^{x^2+y^2} &{}\quad
(11) & f(x,y)= xe^y + 1& {}\quad
(12) & f(x,y)=\cos(x^2 + y^2)
\end{array}\notag
\]
Ejercicio 2. Sea \(r=\Vert(x,y)\Vert =\sqrt{x^2+y^2} \) la distancia al origen desde un punto \((x,y)\) del plano. Comprueba que las curvas de nivel de \( f(x,y)=r^n\) (siendo \( n=0, \pm1, \pm 2,\ldots\)) son circunferencias centradas en el origen. ¿Cómo influye \(n\) en la posición relativa de las circunferencias de nivel entre sí?
Ejercicio 3. Describe cómo son las curvas de nivel de las siguientes superficies y dibújalas:
- El paraboloide de revolución de ecuación \( z=x^2+y^2 \).
- El cono de ecuación \( z=\sqrt{x^2+y^2} \). ¿Qué parecidos y diferencias observas con respecto a las del apartado 1?
- El paraboloide hiperbólico de ecuación \( z=x^2-y^2 \).
- El plano \( z=1+x-y \).
- La superficie de ecuación \( z=\log(1+x-y) \). ¿Qué parecidos y diferencias observas con respecto a las del apartado 4?
- La superficie \( z=\sqrt{1+x-y} \). ¿Qué parecidos y diferencias observas con respecto a las de los apartados 4 y 5?

