1.3. Derivadas parciales
- Page ID
- 49570
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vector}[1]{\vec{\mathbf{#1}}}\)
\( \newcommand{\Disco}{\Bbb D}\)
\( \newcommand{\C}{\Bbb C}\)
\( \newcommand{\Q}{\Bbb Q}\)
\( \newcommand{\R}{\Bbb R}\)
\( \newcommand{\K}{\Bbb K}\)
\( \newcommand{\N}{\Bbb N}\)
\( \newcommand{\Z}{\Bbb Z}\)
\( \newcommand{\bo}{\textbf O}\)
\( \newcommand{\eps}{\varepsilon}\)
\( \newcommand{\la}{\lambda}\)
\( \newcommand{\om}{\omega}\)
\( \newcommand{\bmatriz}{\bmatrix \format \r&&\quad\r\\}\)
\( \newcommand{\bmatrize}{\bmatrix \format \c&&\quad\c\\}\)
\( \newcommand{\sep}{\, \equiv \,}\)
\( \newcommand{\xsep}{\quad \equiv \quad}\)
\( \newcommand{\xlsep}{\qquad \equiv \qquad}\)
\( \newcommand{\matriz}{\bmatrix\format\r&&\quad\r\\}\)
\( \newcommand{\endmatriz}{\endbmatrix}\)
\( \newcommand{\conj}[1]{\overline{}[1]}}\)
\( \newcommand{\vector}[1]{\vec{\textbf {}[1]}}}\)
\( \newcommand{\abs}[1]{\left\vert {#1} \right\vert}}\)
\( \newcommand{\norm}[1]{\left\Vert {#1}\right\Vert}\)
\( \newcommand{\bil}[2]{\left\langle {#1},{#2} \right\rangle}\)
\( \newcommand{\absbil}[2]{\abs{ \bil{#1}{#2} }}\)
\( \newcommand{\vectori}{\vector{\mathbf{\i}}}\)
\( \newcommand{\vectorj}{\vector{\mathbf{\j}}}\)
\( \newcommand{\vectork}{\vector{\mathbf{k}})\)
\( \newcommand{\vectorr}{\vector r}\)
\( \newcommand{\vectorrp}{\vector r}\,{}'}\)
\( \newcommand{\vectorrs}{\vector r}\,{}''}\)
\( \newcommand{\parteim}{\mathop{\text{Im}}\nolimits}\)
\( \newcommand{\partere}{\mathop{\text{Re}}\nolimits}\)
\( \newcommand{\sen}{\mathop{\text{sen}}\nolimits}\)
\( \newcommand{\sinc}{\mathop{\text{sinc}}\nolimits}\)
\( \newcommand{\sa}{\mathop{\text{sa}}\nolimits}\)
\( \newcommand{\senh}{\mathop{\text{senh}}\nolimits}\)
\( \newcommand{\arsenh}{\mathop{\text{arsenh}}\nolimits}\)
\( \newcommand{\arcosh}{\mathop{\text{arcosh}}\nolimits}\)
\( \newcommand{\Log}{\mathop{\text{Log}}\nolimits}\)
\( \newcommand{\Ln}{\mathop{\text{Ln}}\nolimits}\)
\( \newcommand{\Arg}{\mathop{\text{Arg}}\nolimits}\)
\( \newcommand{\arcsen}{\mathop{\text{arcsen}}\nolimits}\)
\( \newcommand{\arcos}{\mathop{\text{arccos}}\nolimits}\)
\( \newcommand{\arctg}{\mathop{\text{arctg}}\nolimits}\)
\( \newcommand{\ran}{\mathop{\text{ran}}\nolimits}\)
\( \newcommand{\maxe}{\mathop{\text{máx}}}\)
\( \newcommand{\mine}{\mathop{\text{mín}}}\)
\( \newcommand{\lime}{\mathop{\text{lím}}}\)
\( \newcommand{\lin}{\mathop{\text{lin}}\nolimits}\)
\( \newcommand{\inte}{\mathop{\text{int}}\nolimits}\)
\( \newcommand{\grad}{\mathop{\text{grad}}\nolimits}\)
\( \newcommand{\signo}{\mathop{\text{sig}}\nolimits}\)
\( \newcommand{\fl}{\mathop{\text{flot}}\nolimits}\)
\( \newcommand{\essup}{\mathop{\text{ess}\,\text{sup}}\nolimits}\)
\( \newcommand{\card}{\mathop{\text{card}}\nolimits}\)
\( \newcommand{\rot}{\mathop{\text{rot}}\nolimits}\)
\( \newcommand{\diver}{\mathop{\text{div}}\nolimits}\)
\( \newcommand{\volum}{\mathop{\text{vol}}\nolimits}\)
\( \newcommand{\Res}{\mathop{\text{Res}}\nolimits}\)
\( \newcommand{\grado}{\mathop{\text{gr}}\nolimits}\)
\( \newcommand{\dpar}[2]{\dfrac{\partial{#1}}{\partial{#2}}}\)
\( \newcommand{\dparx}[1]{\dfrac{\partial {#1}}{\partial x}}}\)
\( \newcommand{\dpary}[1]{\dfrac{\partial {#1}}{\partial y}}}\)
\( \newcommand{\dparz}[1]{\dfrac{\partial {#1}}{\partial z}}}\)
\( \newcommand{\dparr}[1]{\dfrac{\partial {#1}}{\partial r}}}\)
\( \newcommand{\dparth}[1]{\dfrac{\partial {#1}}{\partial \theta}}}\)
\( \newcommand{\dparxx}[1]{\dfrac{\partial^2 {#1}}{\partial x^2}}}\)
\( \newcommand{\dparyy}[1]{\dfrac{\partial^2 {#1}}{\partial y^2}}}\)
\( \newcommand{\dparxy}[1]{\dfrac{\partial^2 {#1}}{\partial x \partial y}}}\)
\( \newcommand{\dparzz}[1]{\dfrac{\partial^2 {#1}}{\partial z^2}}}\)
\( \newcommand{\dparxz}[1]{\dfrac{\partial^2 {#1}}{\partial x \partial z}}}\)
\( \newcommand{\dparyz}[1]{\dfrac{\partial^2 {#1}}{\partial y \partial z}}}\)
\( \newcommand{\dpardos}[2]{\dfrac{\partial^2 {#1}}{\partial {#2}^2}}}\)
\( \newcommand{\dparcruz}[3]{\dfrac{\partial^2 {#1}}{\partial {#2} \partial {#3}}}\)
\( \newcommand{\dtan}[1]{ \dfrac{\partial {#1}}{\partial {\vector t}} }}\)
\( \newcommand{\dnormal}[1]{ \dfrac{\partial {#1}}{\partial {\vector n}} }}\)
Derivadas parciales
El objetivo principal de este capítulo es explicar cómo se extiende el concepto de derivada de una función de una variable a campos escalares de varias variables. El concepto de derivada de una función \( f(x) \) surge como solución del problema de trazar la recta tangente a la curva de ecuación \( y=f(x) \) en un punto. Para un campo de dos variables \( f(x,y) \) nos plantearemos, en la siguiente sección, el problema de hallar el plano tangente a la superficie de ecuación \( z=f(x,y) \) en un punto de dicha superficie y veremos que de dicho planteamiento surge, de manera natural y por analogía con la definición de derivada, la noción de diferencial de un campo escalar de dos variables. En esta analogía desempeñan un papel fundamental las derivadas parciales, que son las que se obtienen derivando una función de varias variables con respecto a una de ellas cuando se dejan las demás constantes. En esta sección estudiamos las derivadas parciales y su interpretación geométrica.
Sea \( f\colon U\to \R \) un campo continuo de dos variables y sea \( (a,b) \) un punto interior del conjunto \( U \). La derivada parcial de \( f \) con respecto a \( x \) en el punto \( (a,b) \) es, si existe el límite, el número
\[ \dfrac{\partial f}{\partial x} (a,b) = \lime_{x \to a} \dfrac{f(x, b)-f(a,b)}{x-a}.\notag\]
O sea, la derivada parcial de \( f \) con respecto a \( x \) en \( (a,b) \) se calcula derivando la función \( f \) con respecto a su variable \( x \) mientras mantenemos su variable \( y \) constante e igual a \( b \).
Análogamente, la derivada parcial de \( f \) con respecto a \( y \) en el punto \( (a,b) \) es, si existe el límite, el número
\[ \dpar{f}{y} (a,b) = \lime_{y \to b} \dfrac{f(a, y)-f(a,b)}{y-b}. \notag\]
O sea, la derivada parcial de \( f \) con respecto a \( y \) en \( (a,b) \) se calcula derivando \( f \) con respecto a \( y \) mientras mantenemos \( x=a \) constante.
Para el caso de tres variables, se definen las derivadas parciales \( \dpar fx, \dpar fy, \dpar fz \) como los valores que se obtienen al derivar con respecto a cada una de las variables manteniendo las otras dos constantes; por ejemplo
\[ \dpar{f}{z} (a,b,c) = \lime_{z \to c} \dfrac{f(a, b, z )-f(a,b,c)}{z-c} .\notag\]
En algunos libros se emplean los incrementos de las variables, \( \Delta x=x-a \), \( \Delta y=y-b \), en los límites que definen las derivadas parciales:
\[\dpar{f}{x} (a,b) =\lime_{\Delta x \to 0} \dfrac{f(a+\Delta x, b)-f(a,b)}{\Delta x} \qquad \dpar{f}{y} (a,b) =\lime_{\Delta y \to 0} \dfrac{f(a, b+ \Delta y)-f(a,b)}{\Delta y},\notag\] y en 3D, tomando por ejemplo \( \Delta z=z-c\),
\[\dpar{f}{z} (a,b,c) =\lime_{\Delta z \to 0} \dfrac{f(a, b, c+\Delta z)-f(a,b,c)}{\Delta z}.\notag\]
Observación práctica importante. En la práctica, para calcular una derivada parcial no se aplica el límite que la define, sino que se emplean las reglas habituales de derivación de funciones de una variable con la variable con respecto a la cual queremos derivar parcialmente, manteniendo constantes las demás variables. Por ejemplo, si tenemos \( f(x,y)=\sen(\pi x^2y)+x-x^3y \) y queremos hallar sus derivadas parciales en el punto \( (1,-2) \) hacemos lo siguiente: para hallar la derivada parcial de \( f \) con respecto a \( x \), suponemos que la \( y \) es constante y derivamos como si \( f \) solo fuera función de \( x \):
\[ \dpar fx = 2 \pi xy\cos( \pi x^2y)+1-3x^2y, \quad\text{luego}\quad \dpar fx(1,-2)=-4\pi\cos(-2\pi)+7=7-4\pi.\notag\]
Para hallar la derivada parcial de \( f \) con respecto a \( y \), suponemos que la \( x \) es constante y derivamos como si \( f \) solo fuera función de \( y \):
\[ \dpar fy = \pi x^2\cos(\pi x^2y)-x^3, \quad\text{luego}\quad \dpar fy(1,-2)= \pi\cos(-2 \pi)-1= \pi-1. \notag\]
Otras notaciones. Hay otras notaciones muy extendidas para denotar las derivadas parciales. Por ejemplo, si expresamos una variable \( u \) como función de \( x,y,z \), digamos \( u=f(x,y,z) \), entonces las derivadas parciales pueden aparecer escritas en diversos textos de las siguientes maneras:
\[ \dpar{f}{x} =f_x = D_x f = u_x = \dpar{u}{x}; \qquad \dpar{f}{y} =f_y = D_y f = u_y=\dpar{u}y; \qquad \dpar{f}{z} =f_z = D_z f = u_z=\dpar{u}z .\notag\]
Nosotros casi siempre usaremos \( \dpar{f}{x} \) o \( f_x \). En algunos casos se manejan campos escalares \( u(x,y,z,t) \) que dependen de tres variables espaciales \( x,y,z \) y del tiempo \( t \). En estos casos, para la derivada parcial con respecto a \( t \) se emplea a menudo la notación de Newton con un punto sobreescrito: \( \dot u= \dpar ut \).
Vector diferencial y gradiente
El vector \( Df(a,b,c)=\left[\dpar{f}x(a,b,c), \, \dpar{f}y(a,b,c), \, \dpar{f}z(a,b,c) \right] \) formado por las derivadas parciales se llama vector diferencial de \( f \) en el punto \( (a,b,c) \). Para campos de dos variables, se suprime la tercera coordenada y el vector diferencial de \( f \) en \( (a,b) \) es \( Df(a,b)=\left[\dpar{f}x(a,b,c), \, \dpar{f}y(a,b,c)\right] \).
En las aplicaciones, las variables \( x, y, z \) de un campo escalar \( f(x,y,z) \) pueden representar diversas magnitudes: presión, volumen y temperatura; precios; ohmios, voltios y amperios; etc. Sin embargo, en muchos modelos de la física el contexto es el espacio tridimensional, en cuyo caso las variables \( x , y, z \) corresponden, específicamente, a longitudes (con signo) y se usan para representar posiciones \( \vecs r=(x,y, z) \); se dice entonces que son variables espaciales. Para este caso, el diferencial de un campo escalar \( Df(\vecs r)=\left[f_x(\vecs r), \, f_y(\vecs r), \, f_z(\vecs r)\right] \) recibe el nombre de vector gradiente de \( f \) en \( \vecs r \) y se representa de las siguientes maneras (el símbolo \( \nabla \) se lee nabla)
\[
Df( \vecs r )=\grad f(\vecs r )= \nabla f(\vecs r )=
\dpar fx {\vecs i} +\dpar fy {\vecs j}+\dpar fz {\vecs k}=\left[f_x(\vecs r ), \, f_y(\vecs r \, f_z(\vecs r))\right].
\notag\]
Para campos de dos variables, se suprime la tercera coordenada, y el gradiente es \[ \grad f = \nabla f = Df =\left[ \dpar{f}x , \, \dpar{f}y \right] = \dpar fx {\vecs i} +\dpar fy {\vecs j} \notag\]
*La distinción entre diferencial y gradiente es, pues, sutil y en la mayoría de los libros de un primer curso de cálculo de varias variables apenas se insiste en ello. No obstante, es una distinción importante en disciplinas como la física, la mecánica o el electromagnetismo. En este texto utilizaremos \( Df \) o \( \nabla f\) indistintamente, con alguna excepción que se indicará oportunamente, aunque trataremos de emplear cada cual según lo que sea tradicional en cada contexto (por ejemplo, \( Df \) para el concepto de diferenciabilidad de la Sección 1.4, pero \( \nabla f\) para la propiedad de ortogonalidad a las curvas de nivel de la Sección 1.5).
Interpretación geométrica de las derivadas parciales
Si consideramos el punto \( P=(a,b,c) \) en la gráfica de \( f \), de manera que \( c=f(a,b) \), y cortamos dicha superficie con el plano de ecuación \( y=b \), obtenemos una curva \( C_1 \) en dicho plano. Entonces la derivada parcial \( f_x(a,b) \) es la pendiente de la recta tangente \( R_1 \) a esta curva en \( P \). Para ver esto, observemos que la curva \( C_1 \) viene dada, por ejemplo, por la parametrización \( {\vecs r}_1(t)=\bigl(t,b,f(t,b)\bigr) \), con lo que \( P={\vecs r}_1(a) \) y un vector tangente a esta curva en el punto \( P \) es \( \vecs {T}_1={\vecs r}\,{}'_1(a)=\bigl(1,0,f_x(a,b)\bigr) \).
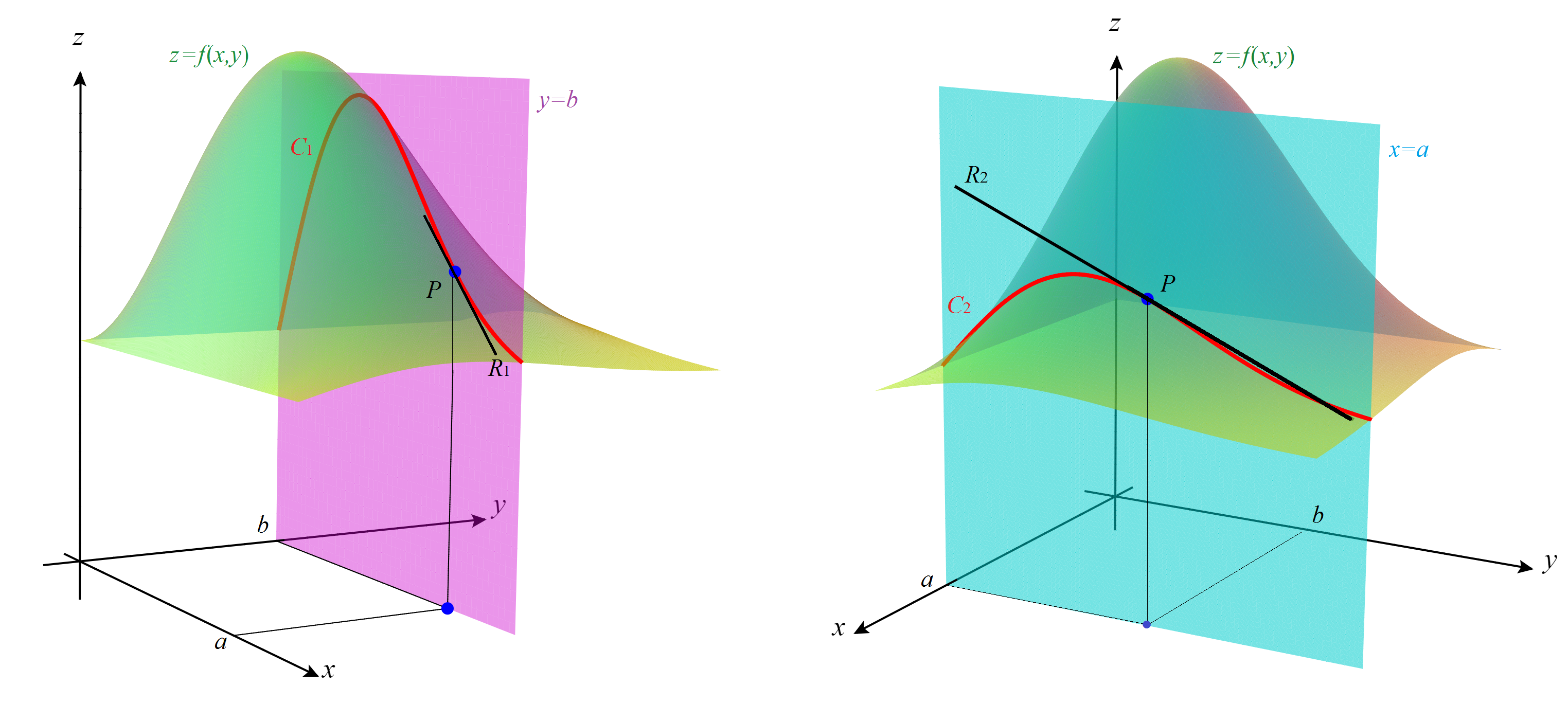
Interpretaciones geométricas de \( \dpar{f}{x} \) (izquierda) y de \( \dpar{f}{y} \) (derecha).
Análogamente, la derivada parcial \( f_y(a,b) \) es la pendiente de la recta tangente \( R_2 \) en el punto \( P \) a la curva \( C_2 \) que resulta de cortar la gráfica de \( f \) con el plano \( x=a \). La curva \( C_2 \) viene dada, por ejemplo, por la parametrización \( {\vecs r}_2(t)=\bigl(a,t,f(a,t)\bigr) \), con lo que \( P={\vecs r}_2(b) \) y un vector tangente a \( C_2 \) en \( P \) es \( \vecs {T}_2=\vecs rp_2(b)=\bigl(0, 1,f_y (a,b)\bigr) \).
En la siguiente sección usaremos estas interpretaciones de las derivadas parciales como las terceras componentes de los vectores \( \vecs {T}_1 \) y \( \vecs {T}_2 \) para resolver el problema de hallar el plano tangente a la superficie \( z=f(x,y) \) en \( P \).
Derivadas parciales segundas
Cuando existen las derivadas parciales de un campo escalar \( f \) en cada punto del dominio \( U \) se pueden definir las funciones derivadas parciales de \( f \), que vienen dadas por
\[
\dpar{f}{x} \colon X \in U \to \dpar{f}{x}(X) \in \R, \qquad
\dpar{f}{y} \colon X \in U \to \dpar{f}{y}(X) \in \R, \qquad
\dpar{f}{z} \colon X \in U \to \dpar{f}{z}(X) \in \R.
\notag\]
En el ejemplo del campo \( f(x,y)=\sen(\pi x^2y)+x-x^3y \), vimos que
\[
\dpar fx (x,y)= 2\pi xy\cos(\pi x^2y)+1-3x^2y,
\qquad
\dpar fy(x,y) = \pi x^2\cos(\pi x^2y)-x^3.
\notag\]
Las derivadas parciales de una función se suelen llamar derivadas parciales de primer orden porque sólo se deriva una vez. A su vez, las funciones derivadas parciales de primer orden podrían ser derivables parcialmente, lo que nos lleva a plantear el proceso de derivación sucesiva introduciendo los conceptos de derivadas parciales segundas, terceras, etc.
Sea \( f\colon U \to \R \) un campo de dos variables para el que existen sus funciones derivadas parciales primeras \( \dpar{f}x, \dpar{f}y\colon U \to \R \). Las derivadas parciales de estas funciones \( \dpar{f}x \) y \( \dpar{f}y \) se llaman, si existen, derivadas parciales segundas de \( f \) y, junto con sus notaciones habituales, son las siguientes:
- Derivada parcial segunda de \( f \) con respecto a \( x \) dos veces \[ \dpar{\left(\dpar{f}{x}\right)}{x}=\dpar{}{x}\left(\dpar{f}{x}\right)=\dfrac{\partial^2 f}{\partial x^2}=f_{xx} =D_{xx}f. \notag\]
- Derivada parcial segunda (o cruzada) de \( f \) primero con respecto a \( x \) y luego con respecto a \( y \) \[\dpar{\left(\dpar{f}{x}\right)}{y}=\dpar{}{y}\left(\dpar{f}{x}\right)=\dfrac{\partial^2 f}{\partial y \partial x}=f_{xy}=D_{xy}f. \notag\]
- Derivada parcial segunda (o cruzada) de \( f \) primero con respecto \( y \) y luego con respecto a \( x \) \[\dpar{\left(\dpar{f}{y}\right)}{x}=\dpar{}{x}\left(\dpar{f}{y}\right)=\dfrac{\partial^2 f}{\partial x \partial y}=f_{yx}=D_{yx}f. \notag\]
- Derivada parcial segunda de \( f \) con respecto a \( y \) dos veces \[\dpar{\left(\dpar{f}{y}\right)}{y}=\dpar{}{y}\left(\dpar{f}{y}\right)=\dfrac{\partial^2 f}{\partial y^2}=f_{yy}=D_{yy}f. \notag\]
Volviendo al ejemplo del campo \( f(x,y)=\sen(\pi x^2y)+x-x^3y \), tendríamos
\[\begin{array}{rl}
f_{xx} &=\dpar{(2\pi xy\cos(\pi x^2y)+1-3x^2y)}{x}
=2\pi y\cos(\pi x^2y)-(2\pi xy)^2\sen(\pi x^2y)-6xy,\\
f_{xy} &=\dpar{(2\pi xy\cos(\pi x^2y)+1-3x^2y)}{y}
=2\pi x\cos(\pi x^2y)-(2\pi xy)(\pi x^2)\sen(\pi x^2y)-3x^2,\\
f_{yx}&=\dpar{(\pi x^2\cos(\pi x^2y)-x^3)}{x}
=2\pi x\cos(\pi x^2y)-\pi x^2(2\pi xy)\sen(\pi x^2y)-3x^2,\\
f_{yy} &=\dpar{(\pi x^2\cos(\pi x^2y)-x^3)}{y}
=-\pi^2 x^4\sen(\pi x^2y).
\end{array}
\notag\]
Observemos que se cumple \( f_{xy}=f_{yx} \); veremos luego que esta igualdad se da casi siempre.
Reiterando el proceso, a partir de las derivadas parciales segundas se definen las derivadas parciales terceras de \( f \), que son ocho, y así sucesivamente.
Para campos de tres variables, hay tres derivadas parciales primeras \( (f_x, f_y, f_z) \), nueve derivadas parciales segundas \( (f_{xx}, f_{xy},f_{xz},f_{yy}, f_{yx},f_{yz},f_{zx}, f_{zy}, f_{zz}) \), 27 derivadas parciales terceras, etc.
Funciones de clase \( C^n \). Sea \( f\colon U \to \R \) un campo escalar continuo con dominio \( U \). Diremos que \( f \) es de clase \( C^n(U) \) si existen todas las derivadas parciales de orden \( 1,2,3,\dots, n \) y son continuas en \( U \) y diremos que \( f \) es de clase \( C^\infty(U) \) si existen sus derivadas parciales de todos los órdenes y son continuas, éste es el caso habitual de los campos que aparecen en las aplicaciones.
Teorema de Clairaut-Schwarz de igualdad de las derivadas cruzadas. Sea \( f\colon U\to \R \) un campo escalar de dos variables de clase \( C^2(U) \). Entonces las derivadas parciales cruzadas son iguales en \( U \), es decir, \( f_{xy}=f_{yx} \) en \( U \).
Para campos de clase \( C^2 \) de tres variables, lo que se verifica es la igualdad entre cada par de derivadas cruzadas: \( f_{xy}=f_{yx} \), \( f_{xz}=f_{zx} \) y \( f_{yz}=f_{zy} \).
Para las derivadas terceras: \( f_{xxy}=f_{xyx} =f_{yxx} \), y así sucesivamente.
[Una demostración]
Matriz hessiana de un campo escalar. Si \( f\colon U \to \R \) es un campo escalar de dos variables de clase \( C^2(U) \), las derivadas parciales segundas de \( f \) se agrupan en una matriz \( D^2 f= \begin{bmatrix} f_{xx}& f_{xy}\\ f_{yx} & f_{yy} \end{bmatrix} \) que es simétrica, por el teorema de Schwarz, y se llama matriz hessiana de \( f \) o diferencial segunda de \( f \) (en el Capítulo 4 veremos por qué).
Cuando el campo escalar depende de tres variables y es de clase \( C^2 \), su matriz hessiana, que también es simétrica por el teorema de Schwarz, es
\[
D^2 f= \begin{bmatrix} f_{xx}& f_{xy} & f_{xz} \\ f_{yx}& f_{yy} & f_{yz} \\ f_{zx}& f_{zy} & f_{zz} \\
\end{bmatrix}.\notag
\notag\]
Ejercicios
Ejercicio 1. Calcula las funciones derivadas parciales de las siguientes funciones y su valor en el origen de coordenadas y el punto \( (1,2) \)
\[\begin{array}{rlrl}
(1) & f(x,y)=\cos(\pi x) + \sen(\pi y) & {}\quad
(2) & f(x,y)=xy &{}\quad
(3) & f(x,y)=5-x^3+xy \\
(4) & f(x,y)=x^2+2xy+3y^2 &{}\quad
(5) & f(x,y)= e^{-(x^2+y^2)/3} &{}\quad
(6) & f(x,y)=\sqrt{x^2+1+y^2} \\
(7) & f(x,y)= (3x+y)\cos(\pi xy) &{}\quad
(8) & f(x,y)= \sqrt{64-x^2} &{}\quad
(9) & f(x,y)= e^{-x} (2y^2-x^2) \\
(10) & f(x,y)=7xy/e^{x^2+y^2} &{}\quad
(11) & f(x,y)= xe^y + 1& {}\quad
(12) & f(x,y)=\cos(x^2 + y^2)
\end{array}
\notag\]
Ejercicio 2. Sea \( r=\norm{(x,y)}=\sqrt{x^2+y^2} \), el radio polar, la distancia al origen desde un punto \( (x,y) \) del plano. Determina el vector diferencial de los campos centrales \( f(x,y)=r^n \) para \( n=\pm1,\pm2,\ldots \) (en el caso \( n=1 \) hay que estudiar con cuidado qué pasa en el origen de coordenadas).
Ejercicio 3. Sean \( \vecs{c}=(a,b) \) un vector de constantes y \( {\textbf A}=\begin{bmatrix} a & b \\ b & c\end{bmatrix} \) una matriz simétrica. Determina el vector diferencial de los siguientes campos:
- La aplicación lineal \(g(x,y)=ax+by \) o, en términos vectoriales, \( g(\vecs{r})=\vecs{c} \cdot \vecs{r} \), donde \( {\vecs r}=(x,y) \) es el vector de posición de un punto en el plano.
- La forma cuadrática \( h(x,y)=ax^2+2bxy+cy^2 \) o, en términos vectoriales, \( h(\vecs {r})=\vecs {r} \cdot {\textbf A} \vecs {r} \).
Ejercicio 4. Formula y haz los Ejercicios 2 y 3 en el caso tridimensional.
Ejercicio 5. Calcula las matrices hessianas de los campos escalares de los Ejercicios 1, 2, 3 Y 4. Comprueba que, en general, la matriz hessiana de la forma cuadrática \( h \) generada por una matriz \( \textbf A\) simétrica es \( D^2h=2{\textbf A} \).
Ejercicio 6. Calcula las derivadas parciales primeras y segundas de los campos
\[ f_1(x,y,z)=xyz, \qquad f_2(x,y,z)=\cos(zx)+\sen(xy) , \qquad f_3(x,y,z)=xz-3xyz+xz^2+2y^2zx, \qquad f_4(x,y,z)=x^2y+xz^2+y^2z. \notag\]
Ejercicio 7. Prueba que los siguientes campos cumplen las ecuaciones que se indican (siendo \( \omega \) una constante positiva):
- \( u(x,t)=e^{-t}\cos(x/\omega) \) cumple la ecuación del calor \( u_t=\omega^2u_{xx} \).
- \( u(x,t)=(x-\omega t)^2 \) cumple la ecuación de ondas \( u_{tt}=\omega^2u_{xx} \).
- \( u(x,t)=\sen(nx)\cos(n\omega t) \) cumple la ecuación de ondas \( u_{tt}=\omega^2u_{xx} \).
- \( u(x,y)=x^2-y^2+xy \) cumple la ecuación de Laplace \( u_{xx}+u_{yy}=0 \).
Ejercicio 8. Las ecuaciones de Cauchy-Riemann ligan las derivadas parciales de dos campos diferenciables \( u,v \) de la siguiente manera
\[\frac{\partial u}{\partial x} =\frac{\partial v}{\partial y} \qquad \text{y} \qquad \frac{\partial u}{\partial y} =-\frac{\partial v}{\partial x} .\notag\]
- Prueba que \( u=x^2-y^2 \) y \( v=2xy \) cumplen las ecuaciones de Cauchy-Riemann.
- Prueba que \( u=e^x\cos(y) \) y \( v=e^x\sen(y) \) cumplen las ecuaciones de Cauchy-Riemann.
- Prueba que si dos campos \( u,v \) de clase \( C^2 \) cumplen las ecuaciones de Cauchy-Riemann, entonces ambos cumplen la ecuación de Laplace \( u_{xx}+u_{yy}=0 \).
*Ejercicio 9. Si no se dan las condiciones del teorema de Clairaut-Schwarz, puede ocurrir que las derivadas parciales cruzadas no sean iguales. Compruébalo con el siguiente ejemplo:
\[ f(x,y)=\begin{cases} xy \dfrac{x^2-y^2}{x^2+y^2} & \text{si }(x,y)\neq (0,0),\\ 0 & \text{si }(x,y)=(0,0). \end{cases} \notag\]
- Prueba que sobre los puntos del eje \( X \) se tiene \( f_y (x,0)=x \) y que sobre los puntos del eje \( Y \) se tiene \( f_y(0,y)=-y \) (aplica directamente sus definiciones como límites).
- Prueba que las derivadas cruzadas de \( f \) son distintas en el origen: \( f_{yx}(0,0)=1\), mientras que \(f_{xy}(0,0)=-1 \) (aplica directamente sus definiciones como límites).
- Prueba que la hipótesis del teorema de Clairaut-Schwarz que no se cumple es la de la continuidad de las derivadas cruzadas en el origen. Para ello, derivando directamente o bien usando la aplicación WolframAlpha, calcula las derivadas parciales cruzadas \( f_{xy} \) y \( f_{yx} \) para \( (x,y) \ne (0,0) \) y calcula sus límites cuando \( (x,y) \to (0,0) \) a lo largo de rectas de la forma \( y=mx \).

