1.6. Las derivadas direccionales y las propiedades del gradiente
- Page ID
- 49594
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vector}[1]{\vec{\mathbf{#1}}}\)
\( \newcommand{\Disco}{\Bbb D}\)
\( \newcommand{\C}{\Bbb C}\)
\( \newcommand{\Q}{\Bbb Q}\)
\( \newcommand{\R}{\Bbb R}\)
\( \newcommand{\K}{\Bbb K}\)
\( \newcommand{\N}{\Bbb N}\)
\( \newcommand{\Z}{\Bbb Z}\)
\( \newcommand{\bo}{\textbf O}\)
\( \newcommand{\eps}{\varepsilon}\)
\( \newcommand{\la}{\lambda}\)
\( \newcommand{\om}{\omega}\)
\( \newcommand{\bmatriz}{\bmatrix \format \r&&\quad\r\\}\)
\( \newcommand{\bmatrize}{\bmatrix \format \c&&\quad\c\\}\)
\( \newcommand{\sep}{\, \equiv \,}\)
\( \newcommand{\xsep}{\quad \equiv \quad}\)
\( \newcommand{\xlsep}{\qquad \equiv \qquad}\)
\( \newcommand{\matriz}{\bmatrix\format\r&&\quad\r\\}\)
\( \newcommand{\endmatriz}{\endbmatrix}\)
\( \newcommand{\conj}[1]{\overline{}[1]}}\)
\( \newcommand{\vector}[1]{\vec{\textbf {}[1]}}}\)
\( \newcommand{\abs}[1]{\left\vert {#1} \right\vert}}\)
\( \newcommand{\norm}[1]{\left\Vert {#1}\right\Vert}\)
\( \newcommand{\bil}[2]{\left\langle {#1},{#2} \right\rangle}\)
\( \newcommand{\absbil}[2]{\abs{ \bil{#1}{#2} }}\)
\( \newcommand{\vectori}{\vector{\mathbf{\i}}}\)
\( \newcommand{\vectorj}{\vector{\mathbf{\j}}}\)
\( \newcommand{\vectork}{\vector{\mathbf{k}})\)
\( \newcommand{\vectorr}{\vector r}\)
\( \newcommand{\vectorrp}{\vector r}\,{}'}\)
\( \newcommand{\vectorrs}{\vector r}\,{}''}\)
\( \newcommand{\parteim}{\mathop{\text{Im}}\nolimits}\)
\( \newcommand{\partere}{\mathop{\text{Re}}\nolimits}\)
\( \newcommand{\sen}{\mathop{\text{sen}}\nolimits}\)
\( \newcommand{\sinc}{\mathop{\text{sinc}}\nolimits}\)
\( \newcommand{\sa}{\mathop{\text{sa}}\nolimits}\)
\( \newcommand{\senh}{\mathop{\text{senh}}\nolimits}\)
\( \newcommand{\arsenh}{\mathop{\text{arsenh}}\nolimits}\)
\( \newcommand{\arcosh}{\mathop{\text{arcosh}}\nolimits}\)
\( \newcommand{\Log}{\mathop{\text{Log}}\nolimits}\)
\( \newcommand{\Ln}{\mathop{\text{Ln}}\nolimits}\)
\( \newcommand{\Arg}{\mathop{\text{Arg}}\nolimits}\)
\( \newcommand{\arcsen}{\mathop{\text{arcsen}}\nolimits}\)
\( \newcommand{\arcos}{\mathop{\text{arccos}}\nolimits}\)
\( \newcommand{\arctg}{\mathop{\text{arctg}}\nolimits}\)
\( \newcommand{\ran}{\mathop{\text{ran}}\nolimits}\)
\( \newcommand{\maxe}{\mathop{\text{máx}}}\)
\( \newcommand{\mine}{\mathop{\text{mín}}}\)
\( \newcommand{\lime}{\mathop{\text{lím}}}\)
\( \newcommand{\lin}{\mathop{\text{lin}}\nolimits}\)
\( \newcommand{\inte}{\mathop{\text{int}}\nolimits}\)
\( \newcommand{\grad}{\mathop{\text{grad}}\nolimits}\)
\( \newcommand{\signo}{\mathop{\text{sig}}\nolimits}\)
\( \newcommand{\fl}{\mathop{\text{flot}}\nolimits}\)
\( \newcommand{\essup}{\mathop{\text{ess}\,\text{sup}}\nolimits}\)
\( \newcommand{\card}{\mathop{\text{card}}\nolimits}\)
\( \newcommand{\rot}{\mathop{\text{rot}}\nolimits}\)
\( \newcommand{\diver}{\mathop{\text{div}}\nolimits}\)
\( \newcommand{\volum}{\mathop{\text{vol}}\nolimits}\)
\( \newcommand{\Res}{\mathop{\text{Res}}\nolimits}\)
\( \newcommand{\grado}{\mathop{\text{gr}}\nolimits}\)
\( \newcommand{\dpar}[2]{\dfrac{\partial{#1}}{\partial{#2}}}\)
\( \newcommand{\dparx}[1]{\dfrac{\partial {#1}}{\partial x}}}\)
\( \newcommand{\dpary}[1]{\dfrac{\partial {#1}}{\partial y}}}\)
\( \newcommand{\dparz}[1]{\dfrac{\partial {#1}}{\partial z}}}\)
\( \newcommand{\dparr}[1]{\dfrac{\partial {#1}}{\partial r}}}\)
\( \newcommand{\dparth}[1]{\dfrac{\partial {#1}}{\partial \theta}}}\)
\( \newcommand{\dparxx}[1]{\dfrac{\partial^2 {#1}}{\partial x^2}}}\)
\( \newcommand{\dparyy}[1]{\dfrac{\partial^2 {#1}}{\partial y^2}}}\)
\( \newcommand{\dparxy}[1]{\dfrac{\partial^2 {#1}}{\partial x \partial y}}}\)
\( \newcommand{\dparzz}[1]{\dfrac{\partial^2 {#1}}{\partial z^2}}}\)
\( \newcommand{\dparxz}[1]{\dfrac{\partial^2 {#1}}{\partial x \partial z}}}\)
\( \newcommand{\dparyz}[1]{\dfrac{\partial^2 {#1}}{\partial y \partial z}}}\)
\( \newcommand{\dpardos}[2]{\dfrac{\partial^2 {#1}}{\partial {#2}^2}}}\)
\( \newcommand{\dparcruz}[3]{\dfrac{\partial^2 {#1}}{\partial {#2} \partial {#3}}}\)
\( \newcommand{\dtan}[1]{ \dfrac{\partial {#1}}{\partial {\vector t}} }}\)
\( \newcommand{\dnormal}[1]{ \dfrac{\partial {#1}}{\partial {\vector n}} }}\)
Derivadas direccionales
La derivada parcial \( f_x(a,b) \) de un campo escalar \(f \) es su tasa de variación cuando nos acercamos al punto \((a,b) \) manteniendo constante \(y=b \), o sea, cuando nos acercamos según la dirección \(\vecs i=(1,0) \). Análogamente, \(f_y(a,b) \) nos da la tasa de cambio de \(f \) al acercarnos según la dirección \( \vecs j=(0,1) \). Podemos plantearnos cómo varía \( f \) cuando nos acercamos según otras direcciones.
Derivada direccional. Sea \( f \colon U \to \R \) un campo escalar de dos o tres variables de clase \( C^1(U) \) y sea \( A \) un punto interior de \( U \). Dado un vector unitario \( \vecs u \), la derivada direccional de \( f \) en la dirección \( \vecs u \) es, si existe el límite, el número
\[ D_{\vecs u} f(A)=\lime_{t \to 0} \frac {f(A+t\vecs{u})-f(A)}{t}. \notag\]
Es decir, si definimos la función de una variable \( \psi(t)=f(A+t\vecs{u}) \), entonces \( D_{\vecs u} f(A)=\psi'(0) \).
Interpretación geométrica de la derivada direccional. Para dos variables, la derivada direccional \( D_{\vecs u}f(a,b) \) da la tasa de cambio de \( f \) al acercarnos al punto \( A=(a,b) \) según la dirección marcada por \( {\vecs u}=(u_1,u_2) \) y admite una interpretación análoga a la de las derivadas parciales.
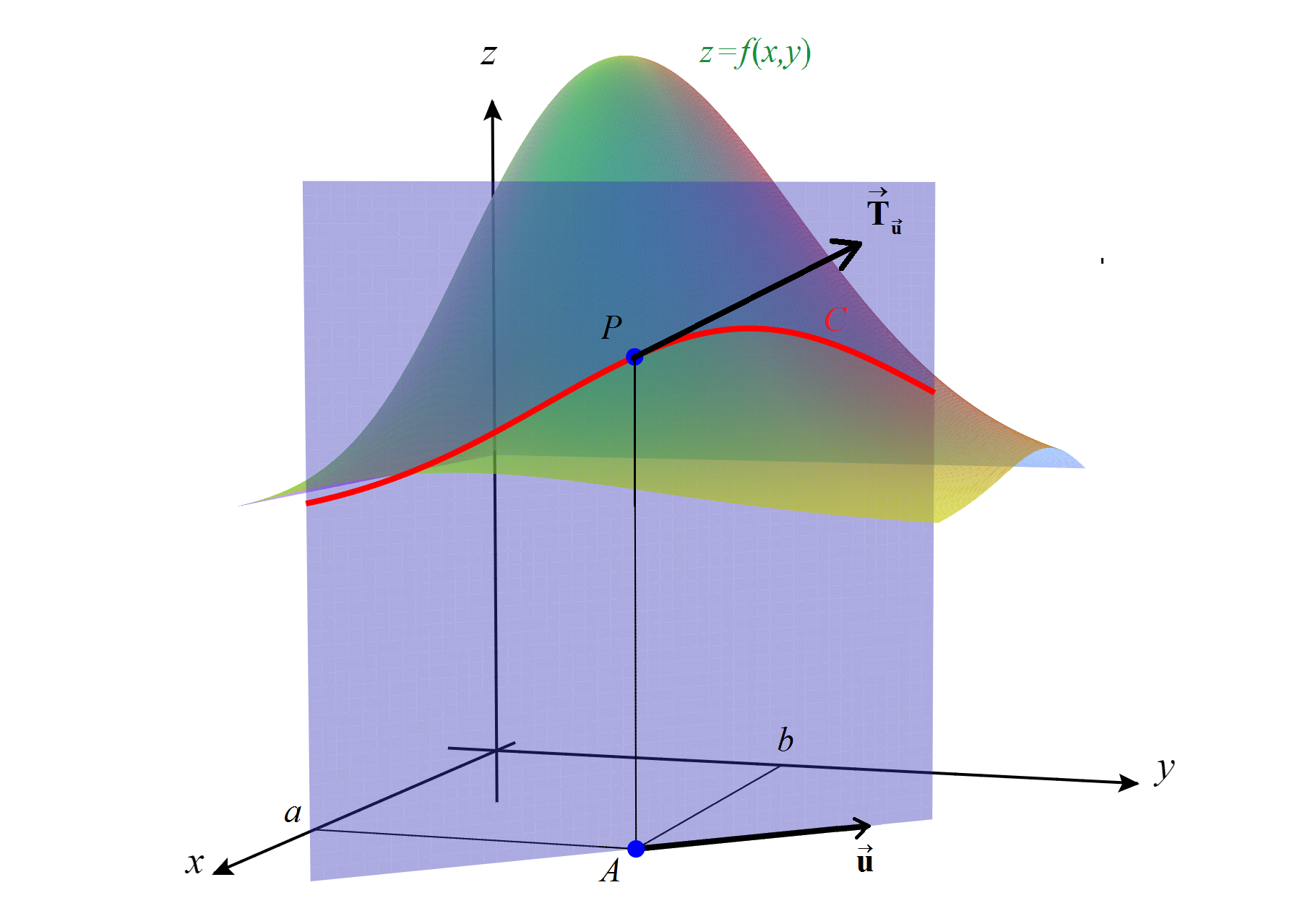
Interpretación geométrica de la derivada direccional.
Si cortamos la gráfica de \( f \), o sea, la superficie \( S \) de ecuación \( z=f(x,y) \), con el plano vertical que pasa por el punto \( P=\bigl(a,b,f(a,b)\bigr) \) y se apoya en la recta del plano \( XY \) que pasa por \( A= (a,b) \) y tiene vector director \( {\vecs u} \), obtenemos una curva \( C \) que está contenida en \( S \) y pasa por \( P \). Entonces la derivada direccional \( D_{\vecs u}f(a,b) \) es la pendiente de la recta tangente a \( C \) en \( P \) como curva en el plano vertical, recta que se conoce como recta tangente a la gráfica de \( f \) según la dirección \( \vecs u \).
La curva \( C \) podemos parametrizarla mediante \( \vecs r(t)=\bigl(a+tu_1,b+tu_2,f(A+t\vecs u)\bigr) \), con lo que \( P=\vecs r(0) \) y un vector tangente a la curva \( C \) en el punto \( P \) es, precisamente, \( \vecs{T}_{\vecs{u}}=\vecs r\,{}'(0)=\left(u_1, u_2,D_{\vecs u}f(a,b)\right) \). Como vimos en la Sección 1.5, el vector \( \vecs{T}_{\vecs{u}} \) debe ser perpendicular al vector \( \vecs n(a,b)=\bigl(-f_x(a,b), -f_x(a,b), 1\bigr) \), que es el vector normal al plano tangente a \( S \) en \( P \). Entonces
\[ 0= \vecs{T}_{\vecs{u}} \cdot \vecs n(a,b) =-u_1 f_x(a,b)-u_2 f_y (a,b) + D_{\vecs u}f(a,b), \notag\]
por tanto, despejando \( D_{\vecs u}f(a,b) \) y usando, como es tradicional en este contexto, el gradiente \( \nabla f=(f_x, f_y) \), obtenemos
\[ D_{\vecs u}f(a,b) = u_1 f_x(a,b) + u_2 f_y (a,b) =\nabla f(a,b) \cdot \vecs u, \notag\]
que es una fórmula muy útil para calcular las derivadas direccionales. Esta fórmula también vale para el caso de un campo escalar de tres variables, como se puede comprobar usando directamente la regla de la cadena.
Propiedades del gradiente
Propiedad de dirección óptima del gradiente. Sean \( f \colon U \to \R \) un campo escalar de dos variables de clase \( C^1(U) \), \( (a,b) \) un punto interior de \( U \) y \( {\vecs u} \) un vector unitario. Si \( \alpha_{\vecs u} \) es el ángulo que forman \( \nabla f(a,b) \) y \( {\vecs u} \), entonces la expresión que acabamos de deducir se puede escribir
\[ D_{\vecs u}f(a,b)=\nabla f(a,b)\cdot\vecs u= \norm{\nabla f(a,b)} \cdot \norm{\vecs u} \cdot \cos\bigl(\alpha_{\vecs u}\bigr) =\norm{\nabla f(a,b)} \cdot \cos\bigl(\alpha_{\vecs u}\bigr). \notag\]
Si \( \nabla f(a,b) \ne 0 \), este valor alcanza su máximo cuando \( \alpha_{\vecs u}=0 \), es decir, cuando \( {\vecs u} =\nabla f(a,b) / \norm{\nabla f(a,b)} \) es el vector unitario de la misma dirección y sentido que el gradiente \( \nabla f(a,b) \), en cuyo caso dicho máximo vale \( \norm{\nabla f(a,b)} \).
Análogamente, el valor mínimo de \( D_{\vecs u}f(a,b) \) se alcanza cuando \( {\vecs u} =-\nabla f(a,b) / \norm{\nabla f(a,b)}\) es el vector unitario de la misma dirección y sentido contrario que \( \nabla f(a,b) \) y dicho valor mínimo es \( -\norm{\nabla f(a,b)} \).
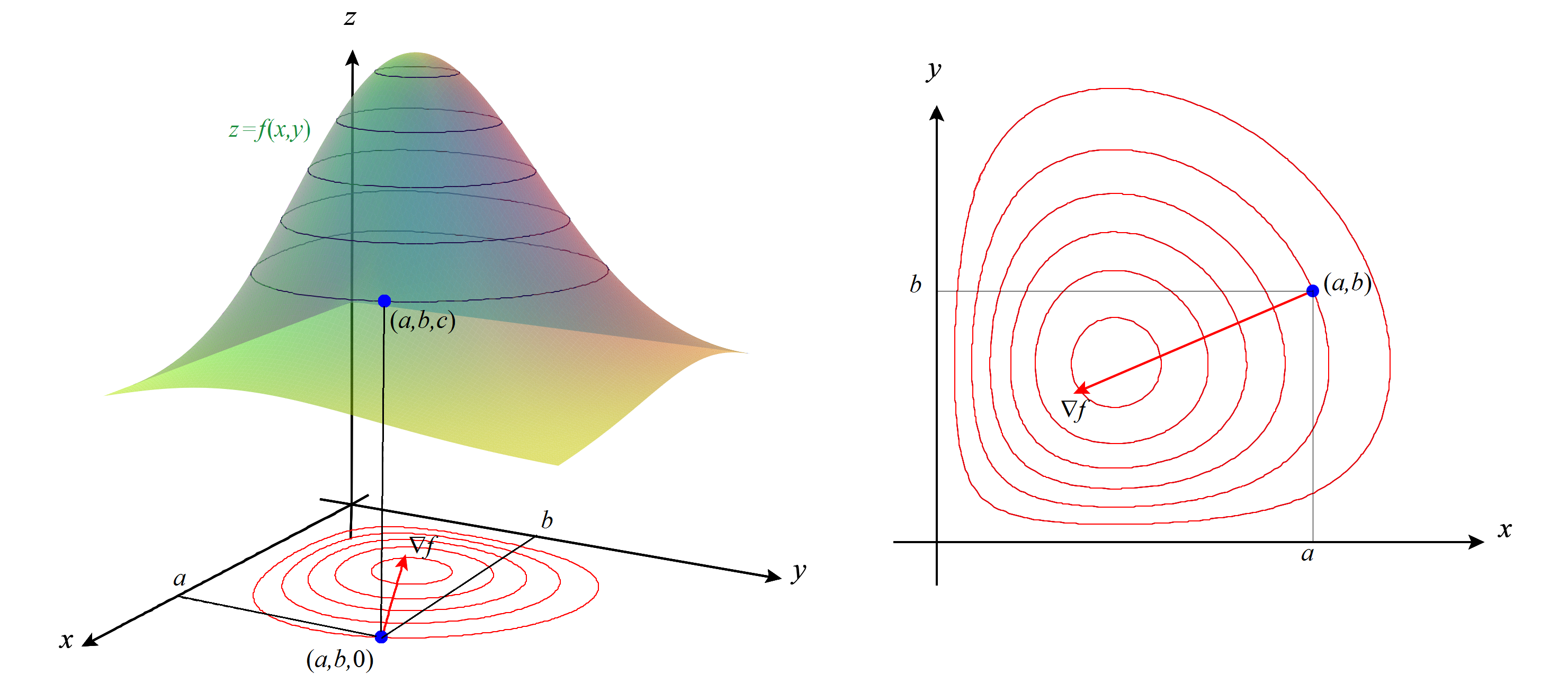
Propiedad de dirección óptima del gradiente.
Esto significa que si consideramos un mapa topográfico de una montaña, el vector gradiente en un punto genérico indicará la dirección de máxima inclinación de subida desde ese punto.
Propiedad de normalidad del gradiente. Sea \( c=f(a,b) \) y consideremos la curva de nivel \( f(x,y)=c \) que pasa por \( (a,b) \). Si dicha curva es regular en el punto \( (a,b) \), entonces el vector gradiente \( \nabla f(a,b) \) es normal a la curva de nivel \( f(x,y)=c \) en dicho punto. En otros términos, si \( \nabla f(a,b) \) no es el vector cero, entonces el vector \( \bigl[-f_y(a,b), \, f_x(a,b)\bigr] \) es tangente a la curva de nivel en \( (a,b) \).
Podemos ver esta propiedad tomando una parametrización de la curva de nivel, digamos \( (x(t), y(t)) \). Entonces \(f (x(t), y(t)) )=c \) para cualquier valor del parámetro \( t \), así que derivando con respecto a \( t \), tenemos \( f_x x'+f_y y'=0 \), luego \( \nabla f=(f_x,f_y) \) es perpendicular al vector tangente a la curva de nivel \( (x',y') \).
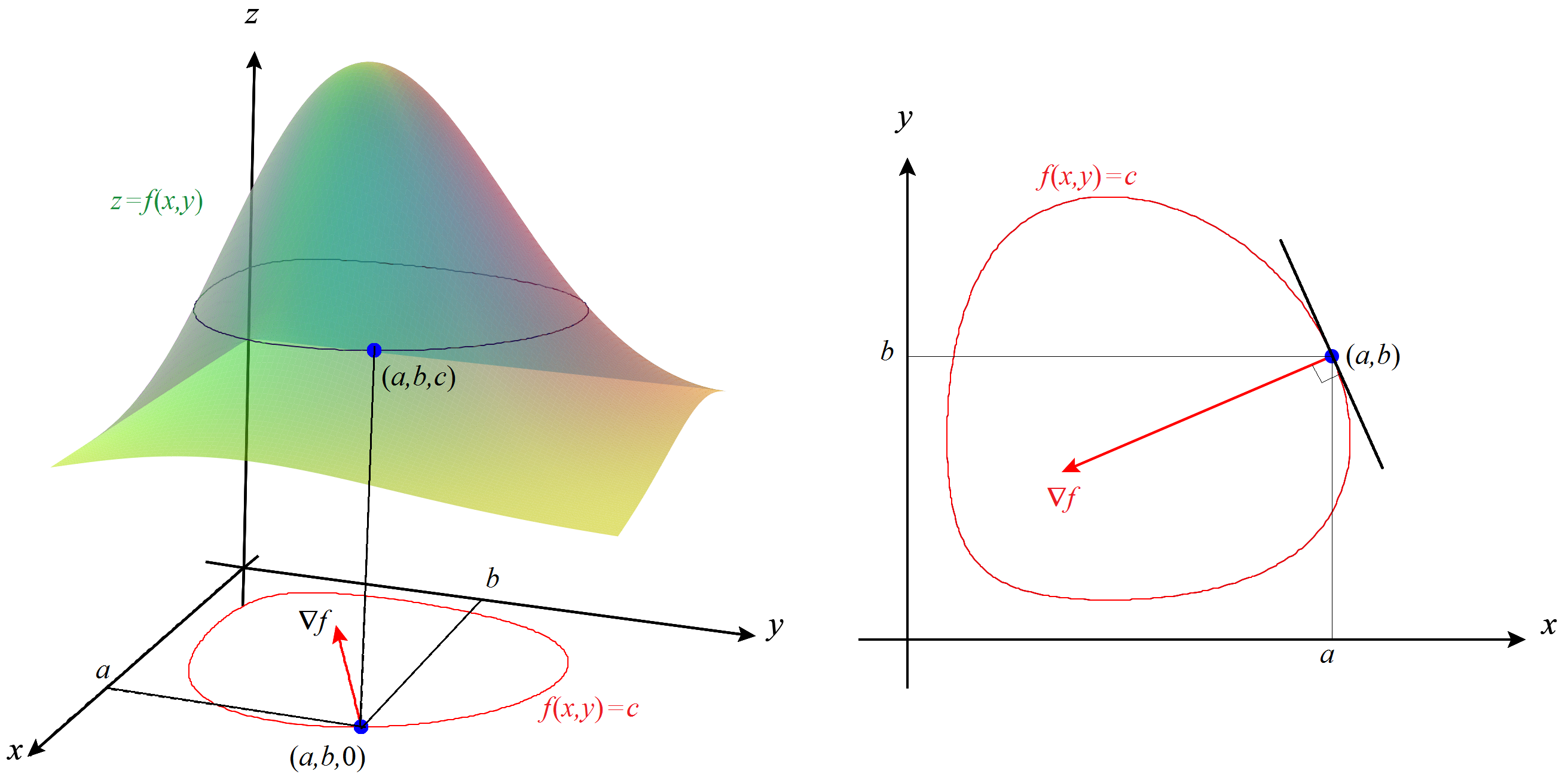
Normalidad del gradiente a la curva de nivel.
Otra forma de verlo es la siguiente: Sea \( C \) la curva que se obtiene al cortar la superficie \(z=f(x,y)\) con el plano horizontal \( z=c\). Entonces dicha curva pasa por \(P=(a,b,c)\) así que la recta tangente \( R \) a la curva \( C \) en \( P \) está contenida en el plano tangente \( z=c+f_x(a,b)(x-a)+f_y(a,b)(y-b) \). Por otro lado, dicha recta tangente \( R \) está contenida en el plano \( z=c \), así que la recta \( R \) es la intersección de los planos \( z=c+f_x(a,b)(x-a)+f_y(a,b)(y-b) \) y \(z=c \). Usamos ahora que la recta tangente a la curva de nivel \( f(x,y)=c \) en el punto \( (a,b) \) es la proyección de \( R \) sobre el plano \(XY\), es decir, la recta que viene dada por la ecuación \( c+f_x(a,b)(x-a)+f_y(a,b)(y-b)=c \) o, lo que es lo mismo, \( f_x(a,b)(x-a)+f_y(a,b)(y-b)=0 \).
Ejercicios
Ejercicio 1. Calcula las derivadas direccionales en la dirección \( {\vecs u} \) que se indica de las siguientes funciones en el origen de coordenadas y el punto \( (1,-1) \).
- \( f(x,y)=x^2+2xy-y^2 \) y \( \vecs u=(\sqrt{2}/2, \sqrt{2}/2) \).
- \( f(x,y)=\sen\bigl(\pi (x+y)\bigr) \cos\bigl(\pi(x-y)\bigr) \) y \( \vecs u=(1/2, \sqrt{3}/2) \).
- \( f(x,y)=1+2x-3xy+y^2 \) y \( \vecs{u}=(-1,0) \).
- \( f(x,y)=e^{xy}-\log(1+x) \) y \( \vecs{u}=(\sqrt{3}/2, -1/2) \).
Ejercicio 2. Sean \( {\vecs r}=(x,y) \) el vector de posición de un punto en el plano y \( r=\norm{\vecs r}=\sqrt{x^2+y^2} \) su distancia al origen. Sean \( \vecs c \) un vector de constantes y \( {\bf A} \) una matriz simétrica de orden 2. Sea \( {\vecs u} \) un vector unitario. Prueba que
\[ D_{\vecs u} \bigl(r^n\bigr)=n r^{n-2} (\vecs r\cdot\vecs u), \qquad D_{\vecs u} \bigl(\vecs{c} \cdot \vecs{r}\bigr)=\vecs c\cdot \vecs u, \qquad D_{\vecs u} \bigl(\vecs{r} \cdot {\bf A} \vecs{r}\bigr)=2\vecs{r}\cdot {\bf A}\vecs u, \notag\]
y comprueba que se dan igualdades análogas en el caso de tres variables.
Ejercicio 3. De un campo escalar diferenciable \( f \) se sabe que en el punto \( P=(1,2) \) su derivada direccional en la dirección desde \( P \) hacia \( A=(2,1) \) vale \( 2 \) y que su derivada direccional en la dirección desde \( P \) hacia \( B=(0,-1) \) vale \( -2 \). Halla el gradiente de \( f \) en \( P \).
Ejercicio 4. Se sabe que \( (1,-1,-2) \) es un punto de una superficie \( z=f(x,y) \) en la que el plano tangente es \( 3x-2y+z=3 \). Sea \( C \) la curva de nivel de \( f \) que pasa por el punto \( (1,-1) \). ¿Cuál es la recta tangente a \( C \) en el punto \( (1,-1) \)?
Ejercicio 5. En un cruce de tres carreteras, la primera va en dirección norte y tiene una pendiente de subida del \( 10 \)\%, la segunda va en dirección suroeste y tiene una pendiente de bajada del \( 5 \)\% y la tercera es horizontal. ¿En qué dirección va la tercera?
Ejercicio 6. Dado el campo escalar \( f(x,y)=x^3y^2+\sen(x+y) \), se pide:
- Halla la ecuación del plano tangente a la gráfica de \( f \) en el punto \( P=(1,\, -1,\, 1) \).
- Halla la ecuación de la recta tangente a la curva de nivel de \( f \) que pasa por \( A= (1, \, -1) \).
- Determina las direcciones \( \vecs{u} \) para las que se tiene \( D_{\vecs u} f(1,\,-1)=4 \).
- Halla las ecuaciones en forma continua de las rectas tangentes a la gráfica de \( f \) en el punto \( P=(1,\, -1,\, 1) \) según las direcciones obtenidas en el apartado (3).
Ejercicio 7. De la gráfica \( z=f(x, \, y) \) de un campo escalar de clase \( C^1(\R^2) \) se sabe que su plano tangente en el punto \( P=(1, \, 2, \, z_0) \) viene dado por la ecuación \( 3x-2y+2z=4 \).
- Calcula \( z_0 \).
- Determina las direcciones \( \vecs u \) para las que \( D_{\vecs u} f(1,\, 2)=2 \).
- Determina si la recta tangente a la gráfica de \( f \) en el punto \( P \) y en la dirección dada por el vector \( \vecs v=\bigl( \sqrt2/2, \, -\sqrt2/2 \bigr) \) pasa por el punto \( Q=(0,\, 1, \, 3 ) \).
- Sea \( C \) la curva de nivel de \( f \) que pasa por el punto \( A=(1, \, 2) \). Halla la ecuación de la recta tangente a \( C \) en el punto \( A \).
Ejercicio 8. Sean \( f \) el campo escalar dado por \( f(x, \, y)=\sqrt{(x-1)(y+2)} \) y \( P \) el punto dado por \( P = (4, \, 1, \, 3) \).
- Halla el dominio \( U \) de \( f \) y determina su frontera y sus puntos interiores.
- Calcula las direcciones unitarias \( \vecs u \) para las que se tiene \( D_{\vecs u}f(4, \, 1) =7/10 \).
- Halla las ecuaciones continuas de las rectas que son tangentes a la gráfica de \( f \) en el punto \( P \) según las direcciones obtenidas en el apartado anterior.
- Hallar la ecuación del plano tangente a la gráfica de \( f \) en el punto \( P \) y comprueba que dicho plano contiene a las rectas btenidas en el apartado anterior.
Ejercicio 9. La figura muestra diversas curvas de nivel de una superficie \( z=f(x,y) \); la más oscura es la que pasa por el punto \( A=(2,1) \). Del campo \( f(x,y) \) se sabe que \( P=(2,1,6) \) está en dicha superficie y que el plano tangente en \( P \) viene dado por \( z=a+2x+y \).
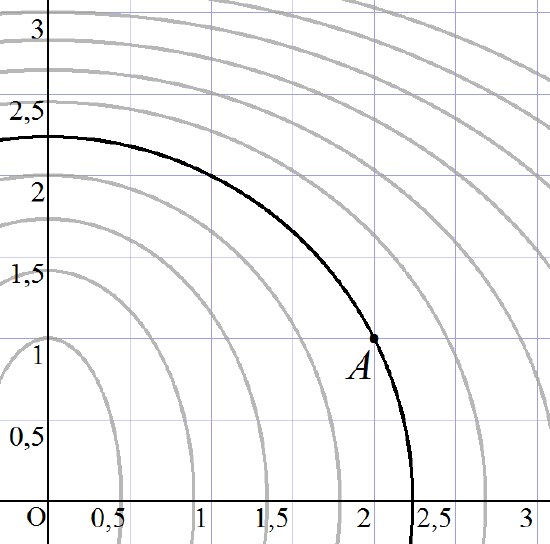
- ¿Cuánto vale el nivel en la curva de nivel que pasa por \( A \)?
- ¿Cuánto vale \( a \)?
- ¿Cuál es el gradiente de \( f \) en \( A=(2,1) \)? Dibújalo en la figura
- ¿Cuál es la ecuación de la recta tangente a la curva de nivel en el punto \( A \)?
Ejercicio 10. Sea \( f(x,y) \) un campo escalar diferenciable en el punto \( A=(-1,0) \). Sabemos que el plano tangente a la superficie de ecuación \( z=f(x,y) \) en el punto \( P=(-1,0, f(A)) \) viene dado por la ecuación \( 2x-y+2z+4=0 \). Sea \( \vecs u=(\sqrt3/2, -1/2) \).
- Calcula \( f(A) \) y la derivada direccional \( D_{\vecs u}f(A) \).
- Halla la recta tangente a la gráfica de \( f \) en \( P \) según la dirección \( \vecs u \).
- Halla la máxima de las derivadas direccionales de \( f \) en \( A \).
Ejercicio 11. Las rectas \( R_1 \) y \( R_2 \) dadas en forma continua por
\[ R_1 \, \equiv \, x=y=\dfrac{z+2}5 \qquad \text{y} \qquad R_2 \, \equiv \, x=\dfrac{y+1}2=\dfrac{z+2}4 \notag\] se cortan en un punto \( P=(x_0,y_0,z_0) \) de la gráfica de un campo escalar \( f(x,y) \) de clase \( C^1(\R^2) \) y, además, ambas están contenidas en el plano tangente en \( P \) a dicha gráfica.
Halla el punto \( P \) y la ecuación del plano tangente a la superficie \( z=f(x,y) \) en el punto \)P \).
Halla el gradiente de \( f \) en el punto \( (x_0,y_0) \).
Halla una dirección unitaria \( \vecs u_1 \) que cumpla lo siguiente: la recta tangente a la gráfica de \( f \) en el punto \( P \) y en la dirección \( \vecs u_1 \) es la recta \( R_1 \).
Halla la ecuación de la recta normal a la curva de nivel de \( f \) que pasa por el punto \( (x_0,y_0) \).
Ejercicio 12. En la figura se muestran diversas curvas de nivel del campo escalar \( f \) definido por \( f(x,y)=5x^2-7xy+y^3 \) y el punto \( P=(1,1) \).
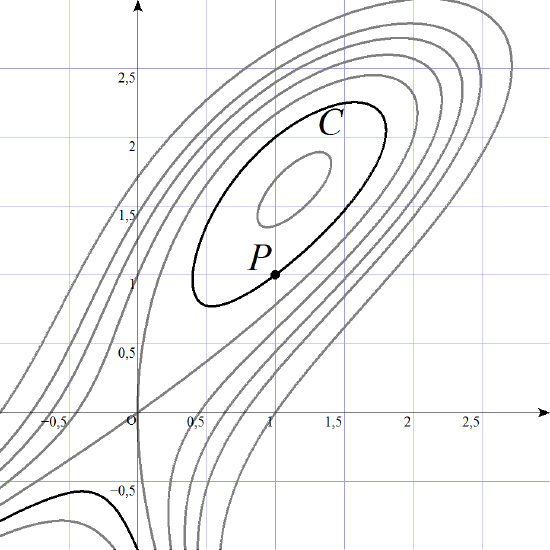
Halla la ecuación del plano tangente a la gráfica de \( f \) en el punto \( Q=\bigl(1,1,f(P)\bigr) \).
Halla la dirección \( \vecs u \) en la que la derivada direccional de \( f \) en \( P \) es máxima, calcula este valor máximo y dibuja el vector \( \vecs u \) en la imagen (situando su origen en \( P \)).
Halla todas las posibles direcciones \( \vecs v \) en las que se cumple que \( D_{\vecs v}f(P)=3 \) y dibuja dichos vectores \( \vecs v \) en la imagen (situando su origen en \( P \)).
En la figura, la curva \( C \) (de color más oscuro) es la curva de nivel que pasa por el punto \( P=(1,1) \). Halla la ecuación de la recta tangente a \( C \) en\( P \).
*Ejercicio 13. Prueba el teorema del valor medio para el gradiente, que establece lo siguiente: Dado un campo escalar \( f \) de clase \( C^1 \) en su dominio \( U \), sean \( A \) y \( B \) puntos interiores de \( U \) de forma que el segmento que une \( A \) con \( B \) está contenido en \( U \). Entonces existe un punto \( C \) en dicho segmento tal que \( f(B)-f(A)=\nabla f(C)\cdot (B-A) \). (Indicación: Parametriza el segmento y aplica el teorema del valor medio para funciones de una variable y la regla de la cadena.)

