1.7. El teorema de Taylor
- Page ID
- 49604
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vector}[1]{\vec{\mathbf{#1}}}\)
\( \newcommand{\Disco}{\Bbb D}\)
\( \newcommand{\C}{\Bbb C}\)
\( \newcommand{\Q}{\Bbb Q}\)
\( \newcommand{\R}{\Bbb R}\)
\( \newcommand{\K}{\Bbb K}\)
\( \newcommand{\N}{\Bbb N}\)
\( \newcommand{\Z}{\Bbb Z}\)
\( \newcommand{\bo}{\textbf O}\)
\( \newcommand{\eps}{\varepsilon}\)
\( \newcommand{\la}{\lambda}\)
\( \newcommand{\om}{\omega}\)
\( \newcommand{\bmatriz}{\bmatrix \format \r&&\quad\r\\}\)
\( \newcommand{\bmatrize}{\bmatrix \format \c&&\quad\c\\}\)
\( \newcommand{\sep}{\, \equiv \,}\)
\( \newcommand{\xsep}{\quad \equiv \quad}\)
\( \newcommand{\xlsep}{\qquad \equiv \qquad}\)
\( \newcommand{\matriz}{\bmatrix\format\r&&\quad\r\\}\)
\( \newcommand{\endmatriz}{\endbmatrix}\)
\( \newcommand{\conj}[1]{\overline{}[1]}}\)
\( \newcommand{\vector}[1]{\vec{\textbf {}[1]}}}\)
\( \newcommand{\abs}[1]{\left\vert {#1} \right\vert}}\)
\( \newcommand{\norm}[1]{\left\Vert {#1}\right\Vert}\)
\( \newcommand{\bil}[2]{\left\langle {#1},{#2} \right\rangle}\)
\( \newcommand{\absbil}[2]{\abs{ \bil{#1}{#2} }}\)
\( \newcommand{\vectori}{\vector{\mathbf{\i}}}\)
\( \newcommand{\vectorj}{\vector{\mathbf{\j}}}\)
\( \newcommand{\vectork}{\vector{\mathbf{k}})\)
\( \newcommand{\vectorr}{\vector r}\)
\( \newcommand{\vectorrp}{\vector r}\,{}'}\)
\( \newcommand{\vectorrs}{\vector r}\,{}''}\)
\( \newcommand{\parteim}{\mathop{\text{Im}}\nolimits}\)
\( \newcommand{\partere}{\mathop{\text{Re}}\nolimits}\)
\( \newcommand{\sen}{\mathop{\text{sen}}\nolimits}\)
\( \newcommand{\sinc}{\mathop{\text{sinc}}\nolimits}\)
\( \newcommand{\sa}{\mathop{\text{sa}}\nolimits}\)
\( \newcommand{\senh}{\mathop{\text{senh}}\nolimits}\)
\( \newcommand{\arsenh}{\mathop{\text{arsenh}}\nolimits}\)
\( \newcommand{\arcosh}{\mathop{\text{arcosh}}\nolimits}\)
\( \newcommand{\Log}{\mathop{\text{Log}}\nolimits}\)
\( \newcommand{\Ln}{\mathop{\text{Ln}}\nolimits}\)
\( \newcommand{\Arg}{\mathop{\text{Arg}}\nolimits}\)
\( \newcommand{\arcsen}{\mathop{\text{arcsen}}\nolimits}\)
\( \newcommand{\arcos}{\mathop{\text{arccos}}\nolimits}\)
\( \newcommand{\arctg}{\mathop{\text{arctg}}\nolimits}\)
\( \newcommand{\ran}{\mathop{\text{ran}}\nolimits}\)
\( \newcommand{\maxe}{\mathop{\text{máx}}}\)
\( \newcommand{\mine}{\mathop{\text{mín}}}\)
\( \newcommand{\lime}{\mathop{\text{lím}}}\)
\( \newcommand{\lin}{\mathop{\text{lin}}\nolimits}\)
\( \newcommand{\inte}{\mathop{\text{int}}\nolimits}\)
\( \newcommand{\grad}{\mathop{\text{grad}}\nolimits}\)
\( \newcommand{\signo}{\mathop{\text{sig}}\nolimits}\)
\( \newcommand{\fl}{\mathop{\text{flot}}\nolimits}\)
\( \newcommand{\essup}{\mathop{\text{ess}\,\text{sup}}\nolimits}\)
\( \newcommand{\card}{\mathop{\text{card}}\nolimits}\)
\( \newcommand{\rot}{\mathop{\text{rot}}\nolimits}\)
\( \newcommand{\diver}{\mathop{\text{div}}\nolimits}\)
\( \newcommand{\volum}{\mathop{\text{vol}}\nolimits}\)
\( \newcommand{\Res}{\mathop{\text{Res}}\nolimits}\)
\( \newcommand{\grado}{\mathop{\text{gr}}\nolimits}\)
\( \newcommand{\dpar}[2]{\dfrac{\partial{#1}}{\partial{#2}}}\)
\( \newcommand{\dparx}[1]{\dfrac{\partial {#1}}{\partial x}}}\)
\( \newcommand{\dpary}[1]{\dfrac{\partial {#1}}{\partial y}}}\)
\( \newcommand{\dparz}[1]{\dfrac{\partial {#1}}{\partial z}}}\)
\( \newcommand{\dparr}[1]{\dfrac{\partial {#1}}{\partial r}}}\)
\( \newcommand{\dparth}[1]{\dfrac{\partial {#1}}{\partial \theta}}}\)
\( \newcommand{\dparxx}[1]{\dfrac{\partial^2 {#1}}{\partial x^2}}}\)
\( \newcommand{\dparyy}[1]{\dfrac{\partial^2 {#1}}{\partial y^2}}}\)
\( \newcommand{\dparxy}[1]{\dfrac{\partial^2 {#1}}{\partial x \partial y}}}\)
\( \newcommand{\dparzz}[1]{\dfrac{\partial^2 {#1}}{\partial z^2}}}\)
\( \newcommand{\dparxz}[1]{\dfrac{\partial^2 {#1}}{\partial x \partial z}}}\)
\( \newcommand{\dparyz}[1]{\dfrac{\partial^2 {#1}}{\partial y \partial z}}}\)
\( \newcommand{\dpardos}[2]{\dfrac{\partial^2 {#1}}{\partial {#2}^2}}}\)
\( \newcommand{\dparcruz}[3]{\dfrac{\partial^2 {#1}}{\partial {#2} \partial {#3}}}\)
\( \newcommand{\dtan}[1]{ \dfrac{\partial {#1}}{\partial {\vector t}} }}\)
\( \newcommand{\dnormal}[1]{ \dfrac{\partial {#1}}{\partial {\vector n}} }}\)
Polinomios de Taylor
En las asignaturas dedicadas al cálculo en una variable habrás estudiado que los polinomios de Taylor se introducen para obtener aproximaciones de los valores de una función de una variable cerca de un punto dado que sean mejores que las dadas por la recta tangente. Recordemos que el polinomio de Taylor \( p_n \) de grado \( n \) de una función \( f \) en un punto \( a \) se construye sabiendo que es el único polinomio de grado \( n \) en el que coinciden su valor y el de sus derivadas hasta orden \( n \) con el valor de la función y de sus derivadas correspondientes en dicho punto, o sea, \( p_n(a)=f(a), p_n'(a)=f'(a), p_n''(a)=f''(a), \ldots, p_n^{(n)}(a)=f^{(n)}(a) \).
Análogamente, para campos escalares de varias variables, los polinomios de Taylor se definen como los polinomios para los que coinciden, en un punto dado, su valor y los de sus derivadas parciales con el valor de la función y los de sus derivadas parciales correspondientes. Su utilidad principal también es la de proporcionar valores aproximados de un campo escalar cerca de dicho punto mejores que las aproximaciones dadas por el plano tangente; que dichas aproximaciones son buenas viene garantizado por el teorema de Taylor, que nos dirá cómo es el error que se comete. Este teorema será también una de las herramientas que usaremos más adelante para la determinación de máximos y mínimos de funciones de varias variables.
En esta sección vamos a trabajar únicamente con dos variables y estudiaremos los polinomios de Taylor de grado \( 1 \)y grado \( 2 \)por comodidad y razones de espacio; es muy fácil extender la formulación para el caso de tres variables, lo que se deja como ejercicio, o para grado mayor que \( 2 \).
Polinomio de Taylor de grado 1 de un campo escalar. Sea \( f:U \to \R \) un campo escalar de dos variables y sea \( (a,b) \)un punto interior del dominio \( U \). Si \( f \) es de clase \( C^1(U) \), el polinomio de Taylor de grado 1 de \( f \) en \( (a,b) \) es
\[ p_1(x,y) = f(a,b)+ f_x(a,b)(x-a)+ f_y (a,b)(y-b). \notag\]
Observemos que \( z=p_1(x,y) \) es la ecuación del plano tangente a la superficie \( z=f(x,y) \) en el punto \( (a,b) \). Si escribimos \( A=(a,b) \), \( X=(x,y) \), entonces \( p_1(X)=f(A)+Df(A)(X-A) \), que es la misma estructura que tiene el polinomio de Taylor para funciones de una variable. De hecho, es fácil ver que el polinomio de Taylor de grado \( 1 \) de \( f \) en \( (a,b) \) es el único polinomio de grado \( 1 \) que cumple que el valor del polinomio y de sus derivadas parciales primeras coinciden con los de \( f \) en \( (a,b) \).
La función \( r_1(x,y)=f(x,y)-p_1(x,y) \) se llama resto de Taylor de orden 1 de \( f \) y sabemos, el resto es lo que aparece en el numerador de la condición de diferenciabilidad, que la aproximación es buena cerca del punto \( (a,b) \); concretamente,
\[\lime_{(x,y) \to (a,b)} \dfrac{r_1(x,y)}{\norm{(x-a,y-b)}}=0.\notag\]
Como en el caso de funciones de una variable, es posible dar una expresión del resto en términos de las derivadas parciales segundas, pero estos va más allá de los objetivos del curso.
Polinomio de Taylor de grado 2 de un campo escalar. Si \( f \in C^2(U) \) entonces podemos mejorar la aproximación lineal obtenida con el plano tangente mediante un polinomio de grado \( 2 \) usando la forma cuadrática generada por matriz hessiana de \( f \), dada por \(D^2 f= \begin{bmatrix} f_{xx} & f_{xy} \\ f_{xy} & f_{yy} \end{bmatrix} \). Se define el polinomio de Taylor de grado 2 de \( f \) en \( A=(a,b) \) como
\[ p_2(X)=f(A)+ Df(A)(X-A) +\tfrac12 (X-A)^T D^2 f (A) (X-A)\notag\]
o, de forma extendida, como
\[p_2(x,y)=f (a,b)+ f_x(a,b) (x-a) + f_y(a,b) (y-b)+ \tfrac12 f_{xx}(a,b) (x-a)^2 + f_{xy}(a,b) (x-a)(y-b)+ \tfrac12 f_{yy}(a,b) (y-b)^2. \notag\]
De nuevo, es fácil ver que el polinomio de Taylor de grado \( 2 \) de \( f \) en \( A=(a,b) \) es el único polinomio de grado \( 2 \) en dos variables tal que su valor y los de sus derivadas parciales primeras y segundas coinciden con los de \( f \) en \( A \).
Teorema de Taylor para un campo escalar. La diferencia \( r_2(x,y)=f(x,y)-p_2(x,y) \) se llama resto de Taylor de orden 2 de \( f \) y cumple que
\[\lime_{(x,y) \to (a,b)} \dfrac{r_2(x,y)}{\norm{(x-a,y-b)}^2}=0.\notag\]
[Idea para una *demostración: dado \( X=(x,y) \) cerca de \(A=(a,b) \), se parametriza el segmento que une \( X \)con \( A \), por ejemplo, mediante \( \vecs r(t)=A+t(X-A) \)con \( 0 \leq t \leq \( 1 \)\), y se aplica el teorema de Taylor para una variable a la función \( \psi(t)=f(\vecs r\bigl( t \bigr) \) usando la regla de la cadena.]
La expresión obtenida nos da garantías de que si \( (x,y) \) está suficientemente cerca de \( (a,b) \), entonces la aproximación de \( f(x,y) \approx p_2(x,y) \) es muy buena. Geométricamente, la gráfica del polinomio de grado \( 2 \) es una cuádrica (generalmente un paraboloide elíptico o hiperbólico) que, en consecuencia, se aproxima bien a la gráfica de \( f \) cerca del punto \( \bigl( a,b,f(a,b) \bigr) \).
En el dibujo vemos la gráfica del campo \( f(x,y) = \dfrac{1}{1+x^2+y^2} \) (en malva) y el paraboloide (en amarillo) que es la gráfica de su polinomio de Taylor de grado 2 en el origen \( p_2(x,y)=1-x^2-y^2 \).
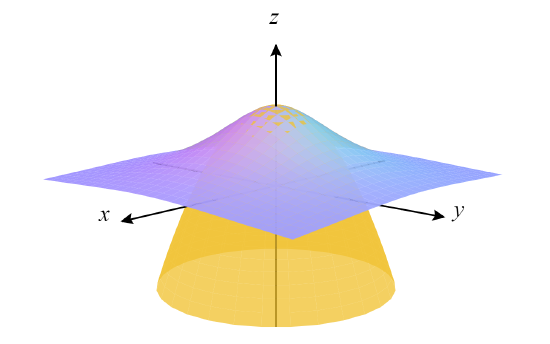
La superficie \( z=(1+x^2+y^2)^{-1} \) y el paraboloide \( z=p_2(x,y)=1-x^2-y^2 \).
Exigiendo la igualdad de las derivadas parciales terceras, cuartas, ..., pueden construirse los polinomios de Taylor de grado \(3,4, \ldots \), con los que, si es necesario, se pueden ir mejorando las aproximaciones.
Observaciones prácticas. Para calcular los polinomios de Taylor debemos, en principio, hallar las derivadas parciales en el punto y construir el polinomio usando la fórmula correspondiente. Sin embargo, podemos ahorrarnos algunos cálculos mediante las siguientes observaciones.
- Suele ser más cómodo calcular los polinomios de Taylor en el origen. Si queremos hallar el polinomio de Taylor \( p \) de \( f \) en un punto \( (a,b)\neq(0,0) \), se puede proceder de la siguiente manera: empezamos haciendo el cambio de variables \( u=x-a \) y\( v=y-b \), luego calculamos el polinomio de Taylor \( q(u,v) \) de \( g(u,v)=f(u+a,v+b) \) en el origen y, finalmente, obtenemos \( p \) deshaciendo el cambio de variables \( p(x,y)=q(x-a, y-b) \).
- Si\( f(x,y) \) es un polinomio de grado tres o superior, entonces el polinomio de Taylor de grado \( 2 \) de \( f \) en el origen se calcula suprimiendo de la expresión de \( f \) los términos de orden superior. Por ejemplo, para hallar el polinomio de grado \( 2 \) de \( f(x,y)=1-2x+y+xy-2y^2+x^3-3x^2y-xy^2 \) en el origen, suprimimos los términos de grado \( 3 \) y obtenemos \( p_2(x,y)=1-2x+y+xy-2y^2 \).
- Si en la expresión de \( f \) aparecen funciones de una variable, podemos usar sus polinomios de Taylor. Por ejemplo, para hallar el polinomio de Taylor de grado \( 2 \)de \( f(x,y)=e^{x+y}\sen(x-y) \) en el origen, usamos que \( 1+t+t^2/2 \) es el polinomio de Maclaurin grado \( 2 \)de \( e^t \) y que \( t \) es el polinomio de Maclaurin grado \( 2 \)de \( \sen(t) \). Sustituyendo \( t=x+y \) en el polinomio de Maclaurin de \( e^t \) y \( t=x-y \) en el del \( \sen(t) \) (en ambos casos \( t=0 \) si \( x=y=0 \)), obtenemos \[ \left( 1+ (x+y)+(x+y)^2/2 \right) (x-y) = x-y+x^2-y^2 +\dfrac{x^3+x^2y-xy^2-y^3}2. \notag\] Finalmente, suprimimos los términos de orden superior a \( 2 \) y obtenemos que el polinomio de Taylor de grado \( 2 \)de \( f(x,y)=e^{x+y}\sen(x-y) \) es \(p_2(x,y)=x-y+x^2-y^2 \).
EJERCICIOS
En los ejercicios 1, 2 y 3, utiliza la aplicación CalcPlot3D para dibujar la gráfica de la función que se da y la del polinomio de Taylor obtenido; observa que cerca del punto practicamente se confunden.
Ejercicio 1. Halla el polinomio de Taylor de grado \( 2 \) de \( f(x,y)=1+(x+y)e^y \) en el origen.
Ejercicio 2. Halla el polinomio de Taylor de grado \( 2 \) de \( f(x,y)=y^2/x^3 \) en el punto \( (1,-1) \).
Ejercicio 3. Halla el polinomio de Taylor de grado \( 2 \) de los siguientes campos en \( (0,0) \) y en \( (1,1) \).
\[ \begin{array}{rlrl}
(1) & f(x,y)=x^2-y^2+xy & {}\quad
(2) & f(x,y)=(x+y)(xy+1)(x^2-2y) \\
(3) & f(x,y)=x^2+y^2+3x^2y+y^3+e^x\cos(y)&{}\quad
(4) & f(x,y)=x\sen(\pi y) + y\sen(\pi x) \\
(5) & f(x,y)=\sen(\pi (x+y))+\cos(\pi(x-y)) &{}\quad
(6) & f(x,y)={xy}/({1+x^2+y^2}) \\
(7) & f(x,y)=1+ 2x-y+x^2+y^2+2xy+3x^3-x^2y &{}\quad
(8) & f(x,y)=e^{x^2+y^2}
\end{array}
\notag\]
Ejercicio 4. Sea \( f(X) \) un campo escalar de tres variables \( X=(x,y,z) \) de clase \( C^2(U) \) y sea \( A=(a,b,c) \) un punto interior de \( U \).
- El polinomio de Taylor de grado \( 1 \) de \( f \) en \( A \) es el único polinomio \( p_1(X) \) de grado \( 1 \) en tres variables que cumple que el valor del polinomio y de sus derivadas parciales primeras coinciden con los de \( f \) en \( A \). Prueba que \( p_1 \) viene dado por la aproximación lineal dada por la diferencial: \(p_1(X)=f(A)+Df(A)(X-A) \).
- El polinomio de Taylor de grado \( 2 \) de \( f \) en \( A \) es el único polinomio \( p_2(X) \) de grado \( 2 \) en tres variables que cumple que el valor del polinomio, de sus derivadas parciales primeras y de sus derivadas parciales segundas coinciden con los de \( f \) en \( A \). Prueba que \( p_2 \) viene dado por \(p_2(X)=f(A)+Df(A)(X-A)+\dfrac12 (X-A)^T D^2f(A) (X-A) \).
- Halla el polinomio de Taylor de grado \( 2 \) en el origen y en el punto \( (-1,0,1) \) de las siguientes funciones: \[ f_1(x,y,z)=z+y^2+z\sen(\pi z)+\log(1+x+z),\quad f_2(x,y,z)=ze^{x+y}\cos(xz) \quad f_3(x,y,z)=\dfrac{\cos(xy+\pi z)}{1+xy}. \notag\]

