2.2. Superficies definidas implícitamente en el espacio
- Page ID
- 49611
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vector}[1]{\vec{\mathbf{#1}}}\)
\( \newcommand{\Disco}{\Bbb D}\)
\( \newcommand{\C}{\Bbb C}\)
\( \newcommand{\Q}{\Bbb Q}\)
\( \newcommand{\R}{\Bbb R}\)
\( \newcommand{\K}{\Bbb K}\)
\( \newcommand{\N}{\Bbb N}\)
\( \newcommand{\Z}{\Bbb Z}\)
\( \newcommand{\bo}{\textbf O}\)
\( \newcommand{\eps}{\varepsilon}\)
\( \newcommand{\la}{\lambda}\)
\( \newcommand{\om}{\omega}\)
\( \newcommand{\bmatriz}{\bmatrix \format \r&&\quad\r\\}\)
\( \newcommand{\bmatrize}{\bmatrix \format \c&&\quad\c\\}\)
\( \newcommand{\sep}{\, \equiv \,}\)
\( \newcommand{\xsep}{\quad \equiv \quad}\)
\( \newcommand{\xlsep}{\qquad \equiv \qquad}\)
\( \newcommand{\matriz}{\bmatrix\format\r&&\quad\r\\}\)
\( \newcommand{\endmatriz}{\endbmatrix}\)
\( \newcommand{\conj}[1]{\overline{}[1]}}\)
\( \newcommand{\vector}[1]{\vec{\textbf {}[1]}}}\)
\( \newcommand{\abs}[1]{\left\vert {#1} \right\vert}}\)
\( \newcommand{\norm}[1]{\left\Vert {#1}\right\Vert}\)
\( \newcommand{\bil}[2]{\left\langle {#1},{#2} \right\rangle}\)
\( \newcommand{\absbil}[2]{\abs{ \bil{#1}{#2} }}\)
\( \newcommand{\vectori}{\vector{\mathbf{\i}}}\)
\( \newcommand{\vectorj}{\vector{\mathbf{\j}}}\)
\( \newcommand{\vectork}{\vector{\mathbf{k}})\)
\( \newcommand{\vectorr}{\vector r}\)
\( \newcommand{\vectorrp}{\vector r}\,{}'}\)
\( \newcommand{\vectorrs}{\vector r}\,{}''}\)
\( \newcommand{\parteim}{\mathop{\text{Im}}\nolimits}\)
\( \newcommand{\partere}{\mathop{\text{Re}}\nolimits}\)
\( \newcommand{\sen}{\mathop{\text{sen}}\nolimits}\)
\( \newcommand{\sinc}{\mathop{\text{sinc}}\nolimits}\)
\( \newcommand{\sa}{\mathop{\text{sa}}\nolimits}\)
\( \newcommand{\senh}{\mathop{\text{senh}}\nolimits}\)
\( \newcommand{\arsenh}{\mathop{\text{arsenh}}\nolimits}\)
\( \newcommand{\arcosh}{\mathop{\text{arcosh}}\nolimits}\)
\( \newcommand{\Log}{\mathop{\text{Log}}\nolimits}\)
\( \newcommand{\Ln}{\mathop{\text{Ln}}\nolimits}\)
\( \newcommand{\Arg}{\mathop{\text{Arg}}\nolimits}\)
\( \newcommand{\arcsen}{\mathop{\text{arcsen}}\nolimits}\)
\( \newcommand{\arcos}{\mathop{\text{arccos}}\nolimits}\)
\( \newcommand{\arctg}{\mathop{\text{arctg}}\nolimits}\)
\( \newcommand{\ran}{\mathop{\text{ran}}\nolimits}\)
\( \newcommand{\maxe}{\mathop{\text{máx}}}\)
\( \newcommand{\mine}{\mathop{\text{mín}}}\)
\( \newcommand{\lime}{\mathop{\text{lím}}}\)
\( \newcommand{\lin}{\mathop{\text{lin}}\nolimits}\)
\( \newcommand{\inte}{\mathop{\text{int}}\nolimits}\)
\( \newcommand{\grad}{\mathop{\text{grad}}\nolimits}\)
\( \newcommand{\signo}{\mathop{\text{sig}}\nolimits}\)
\( \newcommand{\fl}{\mathop{\text{flot}}\nolimits}\)
\( \newcommand{\essup}{\mathop{\text{ess}\,\text{sup}}\nolimits}\)
\( \newcommand{\card}{\mathop{\text{card}}\nolimits}\)
\( \newcommand{\rot}{\mathop{\text{rot}}\nolimits}\)
\( \newcommand{\diver}{\mathop{\text{div}}\nolimits}\)
\( \newcommand{\volum}{\mathop{\text{vol}}\nolimits}\)
\( \newcommand{\Res}{\mathop{\text{Res}}\nolimits}\)
\( \newcommand{\grado}{\mathop{\text{gr}}\nolimits}\)
\( \newcommand{\dpar}[2]{\dfrac{\partial{#1}}{\partial{#2}}}\)
\( \newcommand{\dparx}[1]{\dfrac{\partial {#1}}{\partial x}}}\)
\( \newcommand{\dpary}[1]{\dfrac{\partial {#1}}{\partial y}}}\)
\( \newcommand{\dparz}[1]{\dfrac{\partial {#1}}{\partial z}}}\)
\( \newcommand{\dparr}[1]{\dfrac{\partial {#1}}{\partial r}}}\)
\( \newcommand{\dparth}[1]{\dfrac{\partial {#1}}{\partial \theta}}}\)
\( \newcommand{\dparxx}[1]{\dfrac{\partial^2 {#1}}{\partial x^2}}}\)
\( \newcommand{\dparyy}[1]{\dfrac{\partial^2 {#1}}{\partial y^2}}}\)
\( \newcommand{\dparxy}[1]{\dfrac{\partial^2 {#1}}{\partial x \partial y}}}\)
\( \newcommand{\dparzz}[1]{\dfrac{\partial^2 {#1}}{\partial z^2}}}\)
\( \newcommand{\dparxz}[1]{\dfrac{\partial^2 {#1}}{\partial x \partial z}}}\)
\( \newcommand{\dparyz}[1]{\dfrac{\partial^2 {#1}}{\partial y \partial z}}}\)
\( \newcommand{\dpardos}[2]{\dfrac{\partial^2 {#1}}{\partial {#2}^2}}}\)
\( \newcommand{\dparcruz}[3]{\dfrac{\partial^2 {#1}}{\partial {#2} \partial {#3}}}\)
\( \newcommand{\dtan}[1]{ \dfrac{\partial {#1}}{\partial {\vector t}} }}\)
\( \newcommand{\dnormal}[1]{ \dfrac{\partial {#1}}{\partial {\vector n}} }}\)
Ecuaciones implícitas en el espacio 3D
Si tenemos un campo escalar de tres variables \( F(x,y,z) \), los puntos \( (x,y,z) \) que cumplen \( F(x,y,z)=0 \) forman, en general, una superficie \( S \). Entonces se dice que \( F(x,y,z)=0 \) es la ecuación implícita de \( S \) o que define implícitamente la superficie \( S \). Ya conoces ejemplos de superficies definidas implícitamente, como los planos, dados por ecuaciones de la forma \( ax+by+cz+d=0 \), la esfera unidad, dada por \( x^2+y^2+z^2-1=0 \), y las cuádricas. En esta sección estudiamos el problema de ver qué condiciones garantizan que \( F(x,y,z)=0 \) representa una superficie y si podemos despejar una de las variables en función de las otras dos; por ejemplo, si podemos escribir \( z \) en función de \( x \) e \( y \) para representar la superficie de manera explícita mediante una ecuación \( z=z(x,y) \). La aplicación CalcPlot3D permite dibujar superficies dadas por una ecuación implícita introducida desde el teclado, como el dibujo que se muestra a continuación.
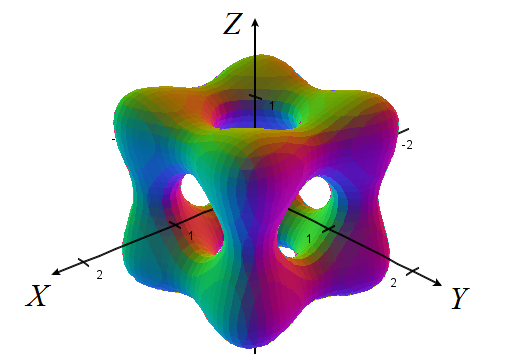
La superficie \( 5(x^4 + y^4 + z^4) - 5(x^2 + y^2 + z^2) +2=0 \).
Plano tangente a una superficie dada de forma implícita. Supongamos que la ecuación \( F(x,y,z)=0 \) define implícitamente una superficie \( S \). Con la regla de la cadena podemos resolver de una manera sencilla el cálculo del plano tangente a \( S \) en un punto \( P=(a,b,c) \). Sea \( C \) una curva regular parametrizada por \( \vecs{r}(t) \), contenida en \( S \) y que pasa por \( P=\vecs{r}(t_0) \). Como \( F\bigl( \vecs{r}(t)\bigr) =0 \) sobre todos los puntos de \( C \), tenemos \( 0 = \left(F\bigl( \vecs{r}(t) \bigr) \right)'=\nabla F(\vecs{r}(t)) \cdot \vecs{r}\,{}'(t) \), lo que para \( t=t_0 \) queda \( \nabla F(P) \cdot \vecs{r}\,{}' (t_0)=0 \). Es decir, el vector \( \nabla F(P) \) es ortogonal al vector tangente a la curva en \( P \). Como \( C \) es cualquier curva regular contenida en \( C \) y que pasa por \( P \), obtenemos que \( \nabla F(P) \) es un vector normal al plano tangente a \( S \) en \( P \).
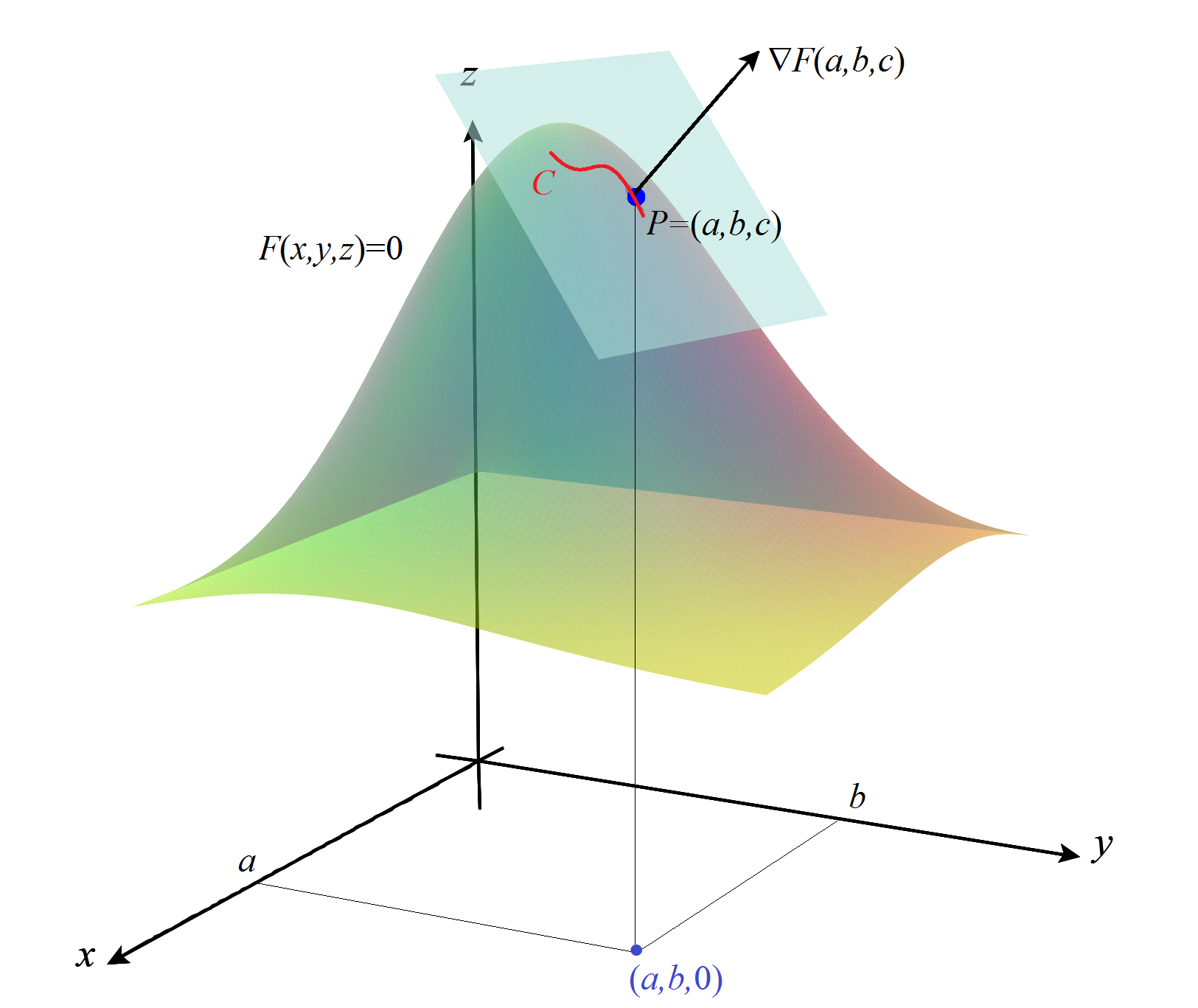
Normalidad del diferencial y plano tangente.
Si \( \nabla F(P)\neq \vecs0 \), el plano tangente vendrá dado por \( F_x(P)(x-a) + F_y(P)(y-b)+F_z(P)(z-c)=0 \). Si pudiéramos despejar \( z=z(x,y) \) entonces sabemos que \( \bigl(-z_x, \, -z_y, \,1\bigr) \) sería un vector perpendicular al plano tangente a \( S \) en el punto \( P \). Como \( \nabla f=\bigl( F_x, \, F_y, \, F_z \bigr) \) también es perpendicular al plano tangente, ambos vectores deben ser paralelos y, por tanto, comparando sus componentes, tendría que cumplirse \( F_z\neq 0 \) y, además, \( z_x=-F_x /F_z \) y \( z_y=-F_y/F_z \). Parece, entonces, que la condición natural ahora es exigir \( F_z\neq 0 \), es decir, que el plano tangente no sea vertical.
Teorema de la función implícita para una superficie en el espacio o para una ecuación con tres variables
Teorema de la función implícita (3D, una ecuación). Sea \( F(x,y,z) \) una función de clase \( C^n(U) \) y sea \( P=(x_0,y_0,z_0) \) un punto interior de \( U \) tal que \( F(P)=0 \) y \( F_z (P) \neq 0 \). Entonces existen un círculo \( D \subset \R^2 \) centrado en \( (x_0,y_0) \) y una única función \( z:D \to \R \) de clase \( C^n(D) \) tales que \( z_0=z(x_0,y_0) \) y que \( z=z(x,y) \) es una solución de la ecuación \( F(x,y,z)=0 \) para cada \( (x,y) \in D \); o sea, \( F\bigl(x,y,z(x,y)\bigr)=0 \) para cada \( (x,y) \in D \). Además, las derivadas parciales de la función \( z(x,y) \) vienen dadas por
\[ \dpar{z(x,y)}x =-\dpar{F\bigl(x,y, z(x,y) \bigr)}x \bigg / \dpar{F\bigl(x,y, z(x,y) \bigr)}z, \qquad \dpar{z(x,y)}y = -\dpar{F\bigl(x,y, z(x,y) \bigr)}y \bigg / \dpar{F\bigl(x,y, z(x,y) \bigr)}z\qquad \text{para cada \( (x,y) \in D\)}. \notag\]
Se dice, entonces, que la ecuación \( F(x,y,z)=0 \) define implícitamente la variable \( z \) como función de las variables \( x,y \) cerca del punto \( P \). Es decir, las soluciones de la ecuación \( F(x,y,z)=0 \) forman una superficie que coincide, cerca del punto \( P \), con la gráfica de la función \( z \).
Los papeles de las variables son intercambiables: si \( F_x\neq 0 \) entonces podemos despejar \( x \) en función de \( y,z \), mientras que si \( F_y\neq 0 \) entonces podemos despejar \( y \) en función de \(x,z\).
Procedimiento de derivación implícita
Usando la regla de la cadena podemos derivar implícitamente \( F\bigl(x,y,z(x,y)\bigr)=0 \), de forma parecida a como lo hemos hecho en la sección anterior, para calcular las derivadas parciales sucesivas de \( z=z(x,y) \) y determinar sus polinomios de Taylor centrados en \( (x_0,y_0) \). Esto nos proporcionará buenas aproximaciones, que pueden ser de utilidad cuando sea imposible obtener \( z (x,y) \) como una fórmula explícita en términos de \( x \) e \( y \). Veamos un ejemplo.
Ejemplo. El origen cumple la ecuación \( F(x,y,z)=z+\sen(z)+x^2+y^2-6xy=0\). Además, \( f \) es un campo escalar de clase \( C^\infty(\R^3)\) para el que se tiene \( \nabla F(x,y,z)=\bigl(2x-6y, 2y-6x, 1+\cos(z) \bigr) \), de manera que \( \nabla F(0,0,0)=(0, 0, 2) \) y el teorema de la función implicita nos garantiza que la ecuación \( F(x,y,z)=0 \) define \( z \) como función de \(x,y \) en un disco \( D \) centrado en el origen y que dicha función \( z(x,y) \) es de clase \( C^\infty (D) \) y cumple \( z(0,0)=0 \) y
\[z(x,y)+\sen(z(x,y))+x^2+y^2-6xy=0, \qquad \text{para \( (x,y) \in D \).}\notag\]
Para determinar el polinomio de Taylor de grado \( 2 \) de \(z(x,y) \) centrado en \( (0,0) \) usaremos el procedimiento de derivación implícita. Para ello, empezamos derivando parcialmente con respecto a \( x \) en la igualdad anterior (en aras de la claridad, no escribiremos los argumentos \( (x,y) \) en las expresiones de las funciones \( z, z_x, z_y, \ldots \) ) obteniendo \( z_x+z_x\cos(z)+2x-6y=0\) para \( (x,y) \in D \). Tomando \(x=0, y=0\), como \(z(0,0)=0\), nos queda \(z_x(0,0)=0\).
Ahora, derivamos parcialmente con respecto a \( y \) en \( z+\sen(z)+x^2+y^2-6xy=0\), y nos queda \( z_y+z_y\cos(z)+2y-6x=0\) para \( (x,y) \in D \). De nuevo, tomando \(x=0, y=0\) obtenemos \( z_y(0,0)=0\).
Para calcular las derivadas segundas \( z_{xx}(0,0), z_{xy}(0,0), z_{yx}(0,0), z_{yy}(0,0) \), derivamos implícitamente en las dos expresiones obtenidas al derivar parcialmente. Así, derivando de nuevo parcialmente con respecto a \( x \) en la igualdad \( z_x+z_x\cos(z)+2x-6y=0 \) obtenida antes, tenemos \( z_{xx}+z_{xx}\cos(z)-(z_x)^2\sen(z)+2=0\) para \( (x,y) \in D \). Usando que para \(x=0, y=0\), tenemos \(z(0,0)=0, z_x(0,0)=0, z_y(0,0)=0\), nos queda \( 2z_{xx}(0,0)+2=0 \) y, por tanto, \( z_{xx}(0,0)=-1 \).
Derivando en la misma expresión \( z_x+z_x\cos(z)+2x-6y=0 \) pero parcialmente con respecto a \( y \), queda \(z_{xy}+z_{xy}\cos(z)-z_xz_y\sen(z)-6=0 \) para \( (x,y) \in D \). Usando de nuevo que si \(x=0, y=0\), entonces \(z(0,0)=0, z_x(0,0)=0, z_y(0,0)=0\), obtenemos \( 2z_{xy}(0,0)-6=0 \) y, por tanto, \(z_{xy}(0,0)=3 \). Como \(z(x,y)\) es de clase \(C^\infty(D)\), el teorema de igualdad de las derivadas cruzadas nos dice que \(z_{yx}(0,0)=3 \)
Finalmente, derivando parcialmente con respecto a \( y \) en la igualdad \( z_y+z_y\cos(z)+2y-6x=0 \) obtenida antes, resulta \( z_{yy}+z_{yy}\cos(z)-(z_y)^2\sen(z)+2=0 \) para \( (x,y) \in D \). Volviendo a usar que si \(x=0, y=0\), entonces \(z(0,0)=0, z_x(0,0)=0, z_y(0,0)=0\), obtenemos, \( 2z_{yy}(0,0)+2=0 \) y, por tanto, \(z_{yy}(0,0)=-1 \).
Con estos resultados, el polinomio de Taylor de grado \( 2 \) de la función implícita \( z=z(x,y) \) en el disco \( D \) definida por la ecuación \(z+\sen(z)+x^2+y^2-6xy=0\) es
\[p_2(x,y)=z(0,0)+z_x(0,0)x+z_y(0,0)y+\dfrac12z_{xx}(0,0)x^2+z_{xy}(0,0)xy+\dfrac12z_{yy}(0,0)y^2 =3xy-\dfrac{x^2+y^2}2.\notag\]
En el dibujo vemos (en colores fríos) la superficie implícita \( z+\sen(z)+x^2+y^2-6xy=0\) y la gráfica (en rojo) del polinomio de Taylor \( p_2(x,y) \) en un disco pequeño centrado en el origen, se parecen tanto que la aplicación mezcla ambas superficies cerca del origen.
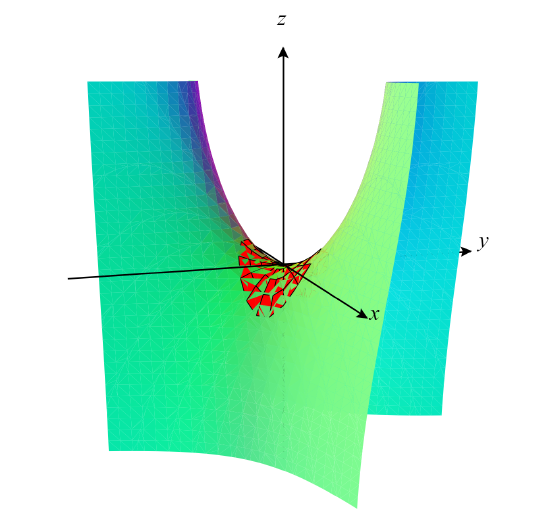
La superficie \( z+\sen(z)+x^2+y^2-6xy=0\) y la gráfica del polinomio de Taylor \( p_2(x,y) \).
Ejercicios
Utiliza la aplicación CalcPlot3D para dibujar las superficies de los ejercicios y, en su caso, las gráficas de los polinomios de Taylor obtenidos.
Ejercicio 1. En los siguientes casos, prueba que la ecuación que se da define implícitamente una superficie \( S \) y calcula el plano tangente a \( S \) en el punto \( P \).
- La ecuación \( x^{2}+y^{2}+3xz+3yz+x+y=0 \) y el punto \( P= (-1,0,0) \).
- La ecuación \( x^3z-z^3yx=0 \) y el punto \( P=(1,1,1) \).
- La ecuación \( x^3-y^3 + 6xy + z^2x = 6 \) y el punto \( P=(1,2,1) \).
Ejercicio 2. Sea \( P=(x,y,z) \) un punto del octante positivo (o sea, \(x,y,z>0\)) que está en la superficie \( S \) dada por la ecuación \( xyz=8 \).
Prueba que el volumen del tetraedro limitado por los planos coordenados y el plano tangente a la superficie \( S \) en \( P \) siempre vale 36.
Ejercicio 3. En los siguientes casos, prueba que la ecuación que se da define implícitamente la variable \( z \) como una función \( z=z(x,y) \) de las
otras variables \(x,y\) cerca del punto \( P \) y calcula el correspondiente polinomio de Taylor de grado \( 2 \) de \( z(x,y) \).
- La ecuación \( z^3+zx^3+zy^4+y^2+2xy-2x-4y+3=0\) y el punto \( P=(1,1,0) \).
- La ecuación \( x^{3}-z^{3}-y^{2}-yx+2z^{2}=0\) y el punto \( P=(1,1,1) \).
- La ecuación \( z\cos (z)+xy=0 \) y el punto \( P= (0,0,0) \).
- La ecuación \( xz^3+z^2y-zy^2-2y+x^2+2=0\) y el punto \( P=(0,1,1) \).
- La ecuación \( y- x \sen(y)= z \) y el punto \( P=(0,0,0) \).
- La ecuación \( y- x \sen(y)= z \) y el punto \( P=(0,a,a) \) con \( a>0\).
- La ecuación \( x^{3}y+y^{2}z^{3}+zx^{2}=3 \) y el punto \( P=(1,-2,1) \).
- La ecuación \( xz-e^zy+1=0 \) y el punto \( P=(-1,\,1,\,0) \).

