6.2 Campos Conservativos
- Page ID
- 2928
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vector}[1]{\vec{\mathbf{#1}}}\)
\( \newcommand{\Disco}{\Bbb D}\)
\( \newcommand{\C}{\Bbb C}\)
\( \newcommand{\Q}{\Bbb Q}\)
\( \newcommand{\R}{\Bbb R}\)
\( \newcommand{\K}{\Bbb K}\)
\( \newcommand{\N}{\Bbb N}\)
\( \newcommand{\Z}{\Bbb Z}\)
\( \newcommand{\bo}{\textbf O}\)
\( \newcommand{\eps}{\varepsilon}\)
\( \newcommand{\la}{\lambda}\)
\( \newcommand{\om}{\omega}\)
\( \newcommand{\bmatriz}{\bmatrix \format \r&&\quad\r\\}\)
\( \newcommand{\bmatrize}{\bmatrix \format \c&&\quad\c\\}\)
\( \newcommand{\sep}{\, \equiv \,}\)
\( \newcommand{\xsep}{\quad \equiv \quad}\)
\( \newcommand{\xlsep}{\qquad \equiv \qquad}\)
\( \newcommand{\matriz}{\bmatrix\format\r&&\quad\r\\}\)
\( \newcommand{\endmatriz}{\endbmatrix}\)
\( \newcommand{\conj}[1]{\overline{}[1]}}\)
\( \newcommand{\vector}[1]{\vec{\textbf {}[1]}}}\)
\( \newcommand{\abs}[1]{\left\vert {#1} \right\vert}}\)
\( \newcommand{\norm}[1]{\left\Vert {#1}\right\Vert}\)
\( \newcommand{\bil}[2]{\left\langle {#1},{#2} \right\rangle}\)
\( \newcommand{\absbil}[2]{\abs{ \bil{#1}{#2} }}\)
\( \newcommand{\vectori}{\vector{\mathbf{\i}}}\)
\( \newcommand{\vectorj}{\vector{\mathbf{\j}}}\)
\( \newcommand{\vectork}{\vector{\mathbf{k}})\)
\( \newcommand{\vectorr}{\vector r}\)
\( \newcommand{\vectorrp}{\vector r}\,{}'}\)
\( \newcommand{\vectorrs}{\vector r}\,{}''}\)
\( \newcommand{\parteim}{\mathop{\text{Im}}\nolimits}\)
\( \newcommand{\partere}{\mathop{\text{Re}}\nolimits}\)
\( \newcommand{\sen}{\mathop{\text{sen}}\nolimits}\)
\( \newcommand{\sinc}{\mathop{\text{sinc}}\nolimits}\)
\( \newcommand{\sa}{\mathop{\text{sa}}\nolimits}\)
\( \newcommand{\senh}{\mathop{\text{senh}}\nolimits}\)
\( \newcommand{\arsenh}{\mathop{\text{arsenh}}\nolimits}\)
\( \newcommand{\arcosh}{\mathop{\text{arcosh}}\nolimits}\)
\( \newcommand{\Log}{\mathop{\text{Log}}\nolimits}\)
\( \newcommand{\Ln}{\mathop{\text{Ln}}\nolimits}\)
\( \newcommand{\Arg}{\mathop{\text{Arg}}\nolimits}\)
\( \newcommand{\arcsen}{\mathop{\text{arcsen}}\nolimits}\)
\( \newcommand{\arcos}{\mathop{\text{arccos}}\nolimits}\)
\( \newcommand{\arctg}{\mathop{\text{arctg}}\nolimits}\)
\( \newcommand{\ran}{\mathop{\text{ran}}\nolimits}\)
\( \newcommand{\maxe}{\mathop{\text{máx}}}\)
\( \newcommand{\mine}{\mathop{\text{mín}}}\)
\( \newcommand{\lime}{\mathop{\text{lím}}}\)
\( \newcommand{\lin}{\mathop{\text{lin}}\nolimits}\)
\( \newcommand{\inte}{\mathop{\text{int}}\nolimits}\)
\( \newcommand{\grad}{\mathop{\text{grad}}\nolimits}\)
\( \newcommand{\signo}{\mathop{\text{sig}}\nolimits}\)
\( \newcommand{\fl}{\mathop{\text{flot}}\nolimits}\)
\( \newcommand{\essup}{\mathop{\text{ess}\,\text{sup}}\nolimits}\)
\( \newcommand{\card}{\mathop{\text{card}}\nolimits}\)
\( \newcommand{\rot}{\mathop{\text{rot}}\nolimits}\)
\( \newcommand{\diver}{\mathop{\text{div}}\nolimits}\)
\( \newcommand{\volum}{\mathop{\text{vol}}\nolimits}\)
\( \newcommand{\Res}{\mathop{\text{Res}}\nolimits}\)
\( \newcommand{\grado}{\mathop{\text{gr}}\nolimits}\)
\( \newcommand{\dpar}[2]{\dfrac{\partial{#1}}{\partial{#2}}}\)
\( \newcommand{\dparx}[1]{\dfrac{\partial {#1}}{\partial x}}}\)
\( \newcommand{\dpary}[1]{\dfrac{\partial {#1}}{\partial y}}}\)
\( \newcommand{\dparz}[1]{\dfrac{\partial {#1}}{\partial z}}}\)
\( \newcommand{\dparr}[1]{\dfrac{\partial {#1}}{\partial r}}}\)
\( \newcommand{\dparth}[1]{\dfrac{\partial {#1}}{\partial \theta}}}\)
\( \newcommand{\dparxx}[1]{\dfrac{\partial^2 {#1}}{\partial x^2}}}\)
\( \newcommand{\dparyy}[1]{\dfrac{\partial^2 {#1}}{\partial y^2}}}\)
\( \newcommand{\dparxy}[1]{\dfrac{\partial^2 {#1}}{\partial x \partial y}}}\)
\( \newcommand{\dparzz}[1]{\dfrac{\partial^2 {#1}}{\partial z^2}}}\)
\( \newcommand{\dparxz}[1]{\dfrac{\partial^2 {#1}}{\partial x \partial z}}}\)
\( \newcommand{\dparyz}[1]{\dfrac{\partial^2 {#1}}{\partial y \partial z}}}\)
\( \newcommand{\dpardos}[2]{\dfrac{\partial^2 {#1}}{\partial {#2}^2}}}\)
\( \newcommand{\dparcruz}[3]{\dfrac{\partial^2 {#1}}{\partial {#2} \partial {#3}}}\)
\( \newcommand{\dtan}[1]{ \dfrac{\partial {#1}}{\partial {\vector t}} }}\)
\( \newcommand{\dnormal}[1]{ \dfrac{\partial {#1}}{\partial {\vector n}} }}\)
Hay ocasiones en las que la integral de un campo vectorial a lo largo de una curva no depende de la curva en sí, sino únicamente de los extremos inicial y final de la curva. Estos campos tienen una gran importancia en las aplicaciones y se llaman campos conservativos; la gravedad newtoniana o la fuerza eléctrica cuando no depende del tiempo son, como veremos, campos conservativos.
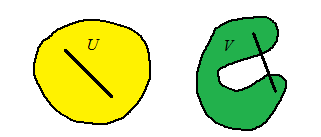
Conjunto conexo. Se dice que un conjunto \(U\) es {conexo} si todo par de puntos de \(U\) se puede unir mediante una curva regular a trozos contenida en \(U\); en otras palabras, si dados dos puntos cualesquiera \(A\) y \(B\) podemos encontrar un camino para ir desde \(A\) hasta \(B\) sin salir de \(U\).

U es conexo. V no es conexo.
Independencia del camino. Sean \(A\) y \(B\) dos puntos de un conjunto conexo \(U\). Se dice que la integral de línea entre \(A\) y \(B\) de un campo vectorial continuo \({\vector F}\) en \(U\) es {independiente del camino seguido para ir desde \(A\) hasta \(B\)} si dadas dos curvas cualesquiera regulares a trozos \(C_1\) y \(C_2\)
contenidas en \(U\) y tales que ambas empiezan en \(A\) y terminan en \(B\), entonces se tiene que \(\int_{C_1} {\vector F} \cdot d{\vector r}=\int_{C_2} {\vector F} \cdot d{\vector r}\). En este caso, dicha integral de línea se suele denotar por \(\int_A^B {\vector F} \cdot d{\vector r}\), notación que hace énfasis solo en los extremos inicial y final, no en el camino que se recorre.
Campo conservativo. Se dice que un campo vectorial continuo \({\vector F}\) es {conservativo} si para cada par de puntos \(A,B \in U\) la integral de línea de \({\vector F}\) entre \(A\) y \(B\) es independiente del camino. Es f{'a}cil ver que un campo vectorial \({\vector F}\) es conservativo en \(U\) si, y solo si, la integral de \({\vector F}\) sobre cualquier curva cerrada, regular a trozos y contenida en \(U\) es cero.
Regla de Barrow para integrales de línea. Sea \(U\) un conjunto conexo y sea \(f: U \) un campo escalar de clase \(C^1(U)\). Sea \(C\) una curva regular a trozos, contenida en \(U\), parametrizada por ${r} U $ con extremo inicial \(A\) y extremo final \(B\). Entonces $ _C fd{r} = f(B)-f(A). $ %s ya que la integral de línea de un gradiente continuo en un %conjunto conexo solo depende de los puntos inicial y final de la curva %sobre la que se integra.
Funci´on potencial. Una consecuencia de este resultado es que si \(\vector F=\nabla f\) es el gradiente de un campo escalar \(f\) de clase \(C^1\) en un conjunto conexo \(U\), entonces \(\vector F\) es un campo conservativo. En este caso se dice que {\footnote“\({}^\dag\)”{En la Física se llama potencial a \(-f\); ésta es una cuesti'on meramente terminológica y obedece a que poniendo el signo ``\({}-{}\)’’ las partículas sometidas a un campo conservativo se mueven en la direcci'on de menor potencial.}% de \({\vector F}\)} y que \(\vector F\) {} Es f{'a}cil ver que dos funciones potenciales cualesquiera de un mismo campo vectorial se diferencian en una constante, como ocurre con las primitivas de una funci'on de una variable.
\(f(x,y)=\int_0^1 (P(tx,ty),Q(tx,ty))\cdot(x,y)\, dt\) x==…=d/dt (tP(tx,ty))
Los campos vectoriales centrales son conservativos. Los campos vectoriales centrales de-ri-van de un potencial, luego son conserva-ti-vos en dominios conexos. Para ver que esto es cierto, sea el campo central \(\vector F(x,y,z)=\psi(r)\vector r\), siendo $r= x+y+z$, \(r=\sqrt{x^2+y^2+z^2}\) y \(\psi\) una funci'on continua en un intervalo del semieje positivo. Si \(f(x,y,z)=\phi(r)\) es un campo escalar central, entonces \(\nabla f=\bigl(\phi'(r)/r\bigr) \bigl(x\vectori+y\vectorj+z\vectork\bigr)\), seg'un hemos visto. Por tanto, tomando \(\phi(r)=\int r\psi(r)\, dr\), tendremos que \(\nabla f=\vector F\), o sea, \(f\) es un potencial de \(\vector F\).
La regla de Barrow nos dice que si un campo vectorial \({\vector F}\) deriva de un potencial en un dominio conexo \(U\) entonces \({\vector F}\) es conservativo en \(U\). Los resultados que siguen permiten dilucidar la cuestión recíproca de si todo campo conservativo deriva de un potencial y, en particular, nos dan una condición manejable para determinar si un campo vectorial dado es conservativo.
Sea \(U\) un conjunto conexo y sea \({\vector F}\) un campo vectorial conservativo en \(U\). Fijamos un punto \(P_0\in U\) y definimos el campo escalar \(f(P)=\int_{C_P} {\vector F} \cdot d{\vector r}\) donde \(C_P\) es cualquier curva regular a trozos y contenida en \(U\) que vaya desde \(P_0\) hasta \(P\). Entonces \(f\) es una función potencial de \({\vector F}\).
Condiciones equivalentes a la de ser un campo conservativo. Sea \({\vector F}\) un campo vectorial continuo en un dominio conexo \(U\), entonces las siguientes condiciones son equivalentes:
- \({\vector F}\) deriva de una función potencial \(f:U \to \R\).
- \({\vector F}\) es conservativo en \(U\).
- Si \(C\) es cualquier curva regular a trozos y cerrada contenida en \(U\), entonces \(\oint_{C} {\vector F} \cdot d{\vector r}=0\).
Observaciones. Si \(\oint_C {\vector F} \cdot d{\vector r} \neq 0\) para una determinada curva cerrada \(C\) en \(U\), en virtud del resultado anterior podemos deducir que \({\vector F}\) {} es un gradiente.
Las condiciones anteriores no son demasiado manejables para determinar si un campo deriva de un potencial. El objetivo del resto de la sección ser{'a} el estudiar una condición necesaria sobre las derivadas parciales de las funciones componentes que es muy {'u}til en la pr{'a}ctica.
%(A.~Clairaut, 1740). Sean \(U\) un conjunto conexo y \({\vector F}=(P,Q,R)\) un campo vectorial de clase \(C^1(U)\). Si \({\vector F}\) deriva de un potencial, entonces \(\rot({\vector F})=\vector 0\); es decir, las derivadas parciales de sus funciones componentes verifican
\(P_y=Q_x\), \(P_z=R_x\) y \(Q_z=R_y\).
\[ \dfrac{\partial P}{\partial y}=\dfrac{\partial Q}{\partial x}, \qquad \dfrac{\partial P}{\partial z}=\dfrac{\partial R}{\partial x} \qquad \text{y}\qquad \dfrac{\partial Q}{\partial z}=\dfrac{\partial R}{\partial y}. \] En el caso bidimensional \({\vector F}=(P,Q)\), esto se reduce a \(P_y=Q_x\). %$= $.
La condición de ser irrotacional es necesaria, pero no es suficiente para asegurar que un campo es conservativo. Es decir, un campo puede ser irrotacional y no ser conservativo; el ejemplo m'as típico es el campo definido por
\[ {\vector F}(x,y)=\left( \frac{-y}{x^2+y^2}, \frac{x}{x^2+y^2}\right) \qquad \text{para $(x,y) \neq(0,0)$.} \] Este campo cumple \(P_y=Q_x\) para \((x,y)\neq (0,0)\), luego \(\rot(\vector F)=0\), pero no es conserva-ti-vo en su dominio de definici'on porque \(\oint_C {\vector F}\cdot d{\vector r}=2\pi\) siendo \(C\) la circunferencia unidad.
El hecho de que un campo sea conservativo no depende exclusivamente de sus compo-nen-tes, sino que tambi'en depende del dominio donde estemos trabajando. En este ejemplo, el problema es que \(C\) rodea el origen, punto en el que \(\vector F\) no est'a definido. Sin embargo, si nos restringimos a un dominio que no rodee al origen, entonces no hay problema. Por ejemplo, el campo anterior sí es conservativo en el semiplano \(x>0\) donde admite la función potencial \(f(x,y)=\arctan(y/x)\).
Se dice que un conjunto \(U\) {} cuando el segmento recto que une dos puntos cualesquiera de \(U\) siempre est{'a} contenido en \(U\). Los conjuntos convexos son una clase especial de conjuntos conexos.
U es convexo, V no es convexo.
Vamos a ver que si el conjunto de referencia es convexo, entonces la condición de ser irrotacional es también suficiente para que un campo sea conservativo. Veremos en la Lecsci'on~8 que esto vale también en otro tipo de conjuntos conexos m'as generales que los convexos.
Sean \(U\) un conjunto convexo y \({\vector F}\) un campo vectorial de clase \(C^1(U)\) tal que \(\rot(\vector F)=\vector 0\). %cuyo rotacional es cero. %%%%%%%%%%%%%
\[ \dfrac{\partial P}{\partial y}=\dfrac{\partial Q}{\partial x}, \qquad \dfrac{\partial P}{\partial z}=\dfrac{\partial R}{\partial x} \qquad\text{y}\qquad \dfrac{\partial Q}{\partial z}=\dfrac{\partial R}{\partial y}. \] %%%%%%%%%%%%%%%%% Entonces \({\vector F}\) deriva de un potencial en \(U\). O sea, en un conjunto convexo ser conservativo y ser irrotacional son equivalentes.
Si aplicando este teorema deducimos que un cierto campo \(\vector F=(P,Q,R)\) deriva de un potencial \(f\) y queremos hallar uno, entonces podemos construir la función potencial que nos da el teorema fundamental del c{'a}lculo para integrales de línea (integrando a lo largo de un segmento, por ejemplo) o bien resolver el sistema \(P_y=Q_x\), \(P_z=R_x\) y \(Q_z=R_y\). %de tres ecuaciones dife-ren-ciales %
\[ %\dfrac{\partial f}{\partial x}=P, \qquad %\dfrac{\partial f}{\partial y}=Q \qquad \text{y}\qquad %\dfrac{\partial f}{\partial z}=R. %\]
El campo vectorial $ {F}(x,y,z)=( y^2+z, , 2xy+z+1, , x+y+1) $ es conservativo en \(\R^3\), que es convexo, porque es de clase \(C^\infty(\R^3)\) e irrotacional:
\[ \rot({\vector F})= {\left\vert\matrix\format\c&&\quad\c\\ \vector i & \vector j & \vector k \\ \partial/\partial x & \partial/\partial y & \partial/\partial z \\ y^2+z & 2xy+z+1 & x+y+1\endmatrix\right\vert} = (0,0,0). \] Para hallar un potencial \(f\) %, o sea, una funci'on \(f\) tal que \(\nabla f=\vector F\) en \(\R^3\), usamos el teorema fundamental del c'alculo para integrales de línea, que dice que podemos obtener \(f\) mediante $ f(x,y,z)=_C F dr $ siendo \(C\) el segmento rectilíneo que une \((0,0,0)\) con \((x,y,z)\).
Parametrizamos \(C\) mediante \(\vector r (t)=(tx, ty, tz)\), con \(t \in [0,1]\), y tenemos
\[ \align f(x,y,z)&=\int_C \vector F \cdot d\vector r = %= \int_0^1 \vector F\bigl(\vector r(t)\bigr) \cdot {\vector r}\,{}'(t) \, dt \\ & = \int_0^1 \bigl( (ty)^2+tz, \, 2(tx)(ty)+tz+1, \, tx+ty+1\bigr) \cdot (x,y,z) \,dt \\ & =\int_0^1 \bigl( 3t^2xy^2+2tzx+2tzy+y+z\bigr) =xy^2+zx+zy+y+z. \endalign \] %donde, para dar el pen'ultimo paso, basta con integrar el primer sumando por partes. Otra manera de obtener un potencial \(f\) es resolver las correspondientes ecuaciones
\[ f_x=y^2+z, \qquad f_y= 2xy+z+1, \qquad f_z=x+y+1. \] Integrando parcialmente la primera con respecto a \(x\) nos queda $ f(x,y,z)=xy^2+zx+ c(y,z) $, donde \(c(y,z)\) es la constante de la integraci'on parcial con respecto a \(x\), constante que podrá depender de las variables \(y,z\). Ahora, derivando parcialmente con respecto a \(y\) en esta expresi'on de \(f\) y usando la segunda de las ecuaciones anteriores, obtenemos $ 2xy+ c_y= f_y = 2xy+z+1, $ de donde obtenemos que \(c_y=z+1\). Integrando parcialmente con respecto a \(y\), queda \(c(y,z)=yz+y+d(z)\), donde \(d(z)\) es la constante de la integraci'on parcial con respecto a \(y\), que podrá depender de \(z\). Tenemos entonces que \(f\) es de la forma \(f(x,y,z)=xy^2+zx+yz+y+d(z)\). Finalmente, derivando con respecto a \(z\) y usando la tercera ecuaci'on, obtenemos $ x+y+d’(z)=f_z = x+y+1, $ con lo que \(d'(z)=1\) y, por tanto, \(d(z)=z+k\), siendo \(k\) una constante. En definitiva, una funci'on potencial de \(\vector F\) es \(f(x,y,z)=xy^2+zx+yz+y+z+k\), donde \(k\) es una constante arbitraria.
En cada uno de los siguientes casos, determina si \({\vector F}\) es o no es el gradiente de un campo escalar en su dominio de definici'on. En caso afirmativo, calcula una función potencial.
\[ \matrix\format\r&\,\,\l&\quad\r&\,\,\l&\quad\r&\,\,\l\\ (1) & {\vector F}(x,y)=(x,y) & (2) & {\vector F}(x,y)=(3x^2y+3, x^3+2y+2) & (3) & {\vector F}(x,y)=(3x^{2}y,x^{3}) \\ (4) & {\vector F}(x,y)= (2xy,x^{2}+1)& (5) & {\vector F}(x,y)=(x+y^{2},2xy) & (6) & {\vector F}(x,y)=(x^{2}+y^{2},0) \endmatrix \]
Sabiendo que el campo ${F}(x,y)=((y)-ay(x)+x,(x)+x(y)+y) $ es conservativo en \(\R^2\), halla el valor de \(a\) y calcula una función potencial \(f\) tal que \(f(1,-1)=1\).
Halla los valores de \(a\) para los que se cumple que \({\vector F}(x,y)=(ax^2y+3, \,x^3+4y+2)\) es un campo vectorial conservativo en \(\R^2\) y halla un potencial \(f\) tal que \(f(1,-1)=3\).
%%%%%%%%%%%%%%%%%%%%% Sea \(\vector F\) el campo vectorial bidimensional dado por
\[
Callstack:
at (Matematicas/Calculo/Calculo_en_Varias_Variables_(ETS_Ingenieria_de_la_Universidad_de_Sevilla)/6._INTEGRALES_DE_LINEA/6.2_Campos_Conservativos), /content/body/p[38]/span, line 1, column 1
Determina los valores de \(a\) y \(b\) sabiendo que \({\vector F}\) es un campo conservativo en \(\R^{2}\) y calcula una función potencial de \({\vector F}\).
Halla la integral de línea $ _{C}
Callstack:
at (Matematicas/Calculo/Calculo_en_Varias_Variables_(ETS_Ingenieria_de_la_Universidad_de_Sevilla)/6._INTEGRALES_DE_LINEA/6.2_Campos_Conservativos), /content/body/p[40]/span[1], line 1, column 1
Sea \({\vector F}\) el campo $ {F}(x,y)=( -{y}/{x^{2}}, {1}/{x}) $ para \(x\neq 0\).
Describe los dominios donde \(\vector F\) es conservativo y halla sus funciones potenciales.
Calcula \(\int_{C}{\vector F}\cdot d{\vector r}\) siendo \(C\) la par{'a}bola que va desde \((2,1)\) hasta \((2,-1)\) pasando por \((9,0)\).
%%%%%%%%%%%%% Usa la regla de Barrow para integrales de línea para hallar la integral de línea del gradiente del campo escalar \(f(x,y)=xy^2\) a lo largo del arco de la par{'a}bola que comienza en el punto \((1,1)\), pasa por el punto \((2,3)\) y termina en el punto \((4,8)\). %%%%%%%%%%%%%
Calcula un potencial de cada uno de los siguientes campos centrales. \(\vector F(x,y,z)=r^n\bigl(x\vectori+y\vectorj+z\vectork\bigr)\) para \(n=0, \pm 1, \pm 2,\dots\) \(\vector F(x,y,z)=\log(r)\bigl(x\vectori+y\vectorj+z\vectork\bigr)\).
\(\vector F(x,y,z)=e^{-r}\bigl(x\vectori+y\vectorj+z\vectork\bigr)\).
En cada uno de los siguientes casos, determina si el campo tridimensional \({\vector F}\) es o no es el gradiente de un campo escalar en su dominio de definici'on o en alguna parte conexa del mismo. En caso afirmativo, calcula una función potencial.
\[ \matrix\format\r&\,\,\l&\qquad\r&\,\,\l\\ (1) & {\vector F}(x,y,z)=(x,y,z) & (2) & {\vector F}(x,y,z)=(x^2,y^2,z^2) \\ (3) & {\vector F}(x,y,z)=(2xyz, x^2z,x^2y) & (4) & \vector F(x,y,z)=\bigl( y \sen(z), \, x\sen(z), \, xy\cos(z)\bigr) \\ (5) & {\vector F}(x,y,z)=(x^{2}y,x^{3}z,2x) & (6) & {\vector F}(x,y,z)=(\cos(yz)+x, z\cos(yz),y\cos(yz)) \\ (7) & {\vector F}(x,y,z)=(x+y^{2},2xy, 2z) & (8) & {\vector F}(x,y,z)=(x^{2}+y^{2}+z^2,0,0) \\ (9) & {\vector F}(x,y,z)=(x+z,-y-z,x-y) & (10) & \vector F(x,y,z)=\left(2ye^{2x}-1/{x},e^{2x},z\right) \endmatrix \]
El campo $ F(x,y,z)=( y z (x z)+az, , (x z), , y x (x z)+4x) $ es conserva-tivo en \(\R^3\). Halla \(a\) y calcula \( \oint_{C_1} \vector F \cdot d\vector r\) y \( \int_{C_2} \vector F \cdot d\vector r\) siendo \(C_1\) y \(C_2\) las curvas regulares que se muestran en la figura.
Dados el campo vectorial \(\vector F(x,y,z)=\bigl(2xyz^{3}+ye^{xy},\,x^{2}z^{3}+xe^{xy},\,3yx^{2}z^{2}+\cos (z)\bigr)\) y la superficie esf'{e}rica \(S\) de centro el origen y radio \(\pi /2\), se pide:
Estudiar si \(\vector F\) es conservativo en \(\R^3\) y, en caso afirmativo, encontrar una funci'on potencial.
Hallar \(\int_{C_{1}} \vector F \cdot d\vector r\) siendo \(C_{1}\) un meridiano de \(S\) recorrido desde el polo norte hasta el sur.
Calcular \(\oint_{C_{2}} \vector F \cdot d\vector r\) siendo \(C_{2}\) el paralelo que se obtiene al cortar \(S\) con el plano \(z=1\).
Sea \(\vector F\) el campo vectorial definido para todos los puntos \((x,y,z)\) con \(z \neq 0\) por
Prueba que \(\vector F\) es irrotacional en todo su dominio de definici'on.
Prueba que \(\vector F\) es conservativo en el conjunto \(W\) formado por los puntos \((x,y,z)\) con \(z>0\). ?`Es \(\vector F\) conservativo en todo su dominio de definici'on? Justifica la respuesta.
Calcula una funci'on potencial de \(\vector F\) en \(W\).
Calcula la circulaci'on \(\oint_C\vector F \cdot d \vector r\) de \(\vector F\) alrededor de la elipse \(C\) que se obtiene al cortar el cilindro \(x^2+y^2=1\) con el plano \(y+z=2\), recorrida en sentido positivo cuando se mira desde arriba.
Calcula la integral de línea de \(\vector F\) sobre la espiral dada por \(\vector r(t)=\bigl( e^t\cos(t), \, e^t\sen(t), \, e^t \bigr)\) para \(0\leq t \leq 2\pi\).
Halla los valores de \(a\) y \(b\) para los que \(\vector F(x,y,z)=\bigl(ay\sen(z), \,bx\sen(z), \,abxy\cos(z) \bigr)\) es un campo conservativo en \(\R^3\) y, para dichos casos, calcula una funci'on potencial de \(\vector F\).
%%%%%%%%%%%%% GREEN A LA LECCIÓN 8 %%%%%%%%%%%%%%%%%%%%%
%En {Matem'aticas II} se vieron algunas ecuaciones diferenciales %que pueden resolverse explícita-men-te. %: las ecuaciones en %variables separadas y las lineales. Vamos a estudiar ahora una clase de ecuaciones diferenciales de primer orden que pueden resolverse explícitamente, al igual que las separables y las lineales vistas en {Matem'aticas II}.
Sea \(f(x,y)\) un campo escalar de clase \(C^1\) en su dominio con gradiente \(\nabla f(x,y)=\bigl[ P(x,y), \,Q(x,y) \bigr]\). Supongamos que en una curva de nivel \(f(x,y)=c\), la variable \(y\) es una función derivable \(y=y(x)\) de \(x\). Entonces, al derivar \(f(x,y(x))=c\), obtenemos que \(y\) es una solución de la ecuación diferencial \(P(x,y)+Q(x,y)y'=0\).
%(A.~Clairaut, 1740). Sean \(P(x,y)\) y \(Q(x,y)\) dos campos escalares continuos en un conjunto conexo \(U \subset \R^2\). Diremos que \(P(x,y)+Q(x,y)y'=0\) es {} si el campo \({\vector F}(x,y)=\bigl(P(x,y),\, Q(x,y) \bigr)\) deriva de un potencial \(f(x,y)\) de clase \(C^1(U)\). En ese caso, la solución general de dicha ecuación es \(f(x,y)=c\). En particular, para que la ecuación sea exacta basta con que \(U\) sea un conjunto convexo en el que se verifique \(P_y=Q_x\). %\(\dfrac{\partial P}{\partial y}=\dfrac{\partial Q}{\partial x}\).
La ecuación \(y^2e^{xy}+(1+xy)y'e^{xy}=0\) es exacta porque $ [y2e{xy}]_y= [(1+xy)e^{xy}]_x %=(2y+y2x)e{xy}, $, con lo que \({\vector F}=(y^2e^{xy}, (1+xy)e^{xy})\) deriva de una función potencial \(f\) en todo el plano. Para hallar \(f\), integramos \(f_x=y^2e^{xy}\) con respecto a \(x\) y obtenemos $ f(x,y)=ye^{xy}+h(y) $ donde \(h\) es una función que solo depende de \(y\) (la ``constante’’ de la integraci'on con respecto a \(x\)). Derivando esta expresi'on de \(f\) con respecto a \(y\) y usando que \(f_y= (1+xy)e^{xy}\), queda \(h'(y)=0\) y, por tanto, \(h\) es constante. En resumen, una función potencial es \(f(x,y)=ye^{xy}\) y la solución general de la ecuación diferencial es \(ye^{xy}=c\), siendo \(c\) una constante cualquiera.
Observemos lo siguiente: Como \(e^{xy} \neq 0\), resulta que \(y^2e^{xy}+(1+xy)y'e^{xy}=0\) tiene las mismas soluciones que \(y^2 +(1+xy)y' =0\). Sin embargo, esta {'u}ltima no es exacta; al simplificar \(e^{xy}\) pierde esa cualidad. Por eso, el término \(e^{xy}\) se llama factor integrante de la ecuación \(y^2 +(1+xy)y' =0\).
Sean \(P(x,y)\) y \(Q(x,y)\) dos campos escalares continuos en un dominio conexo. Diremos que \(\mu(x,y)\) es {} de la ecuación $ P(x,y)+Q(x,y)y’=0 $ cuando, al multiplicar por \(\mu(x,y)\), la ecuación resultante $ (x,y)P(x,y)+(x,y)Q(x,y)y’=0 $ es una ecuación diferencial exacta. En consecuencia, si se puede encontrar un factor integrante, lo que no siempre es posible o f'acil, entonces se puede resolver la ecuaci'on hallando un potencial del campo \((\mu P, \mu Q)\).
%%%%%%%%%%%%% Si \(\mu(x,y)\) es un factor integrante de \(P(x,y)+Q(x,y)y'=0\), entonces se cumple \(\mu_yP-\mu_xQ=\bigl(Q_x-P_y\bigr)\mu\).
P- Q= (-). \]
Por tanto, para buscar un factor integrante debemos resolver esta ecuaci'on, lo que no siempre es posible, ni f'acil, salvo en algunos casos especiales. %%%%%%%%%%%%%
Resuelve el problema de valor inicial \((2x+2y)+(6y+2x-1)y'=0\) con \(y(2)=-1\), probando previamente que la ecuaci'on diferencial es exacta.
Sabiendo que \(y(6x-1)+(3x^2+3y^2-ax)y'=0\) es exacta, calcula \(a\) y resuelve el problema de valor inicial \(y(0)=8\) para dicho valor de \(a\).
Resuelve las siguientes ecuaciones diferenciales exactas.
\[ \matrix\format\r&\quad\l&\qquad\r&\quad\l\\ (1) & 2xy+(x^2-1)y'=0 & (2) & 2xy+(x^2-y^2)y'=0 \\ (3) & y^2-2x+2xyy'=0 & (4) & (x-y^2)-(2xy+y)y'=0\\ (5) & 2x^{3}+3y +\left( 3x+y-1\right) y'=0 & (6) & x-2y+\left(6y-2x+1\right)y'=0 \\ (7) & e^x+3y^2+6xyy'=0 & (8) & 3y+e^x + (3x + \cos(y))y'=0 \endmatrix \]
Resuelve el problema de valor inicial \(x^2-y^2+2xyy'=0\) con \(y(1)=3\) sabiendo que la ecuaci'on diferencial admite un factor integrante que solo depende de \(x\).
Resuelve estas ecuaciones hallando un factor inte-gran-te que solo depende de \(x\).
\[ \matrix\format\r&\quad\l&\qquad\r&\quad\l\\ (1) & y+(x^2-x)y'=0 & (2) & (2y^2+9xy)+(2xy+3x^2)y'=0 \\ (3) & 3xy-2y^3+(x^2-3xy^2)y'=0 & (4) & 3xy+2y^2+(x^2+2xy)y'=0 \endmatrix \]
Resuelve estas ecuaciones hallando un factor inte-gran-te que solo depende de \(y\).
\[ \matrix\format\r&\quad\l&\qquad\r&\quad\l\\ (1) & y+(2x+3y)y'=0 & (2) & (2xy+y^4)+(3x^2+6xy^3)y'=0 \\ (3) & y^2 \cos(x) + \bigl(4+5y \sen(x)\bigr) y'=0 & (4) & 2xy^2+(3yx^2+2)y'=0 \endmatrix \]
Considera la ecuaci'on diferencial \((3x^2+3y\cos(x))+(x^3+3(1+y)\sen(x))y'=0\).
Prueba que no es una ecuaci'on diferencial exacta en el plano.
Halla un factor integrante de dicha ecuaci'on que solo dependa de \(y\).
Calcula la soluci'on general de la ecuaci'on.
Resuelve el correspondiente problema de valor inicial con \(y(\pi)=0\).
Resuelve
\(2y-6x+(3x- {4x^{2}}/{y})y'=0\) , hallando un factor integrante \(\mu (x,y)=xy^{a}\).
Resuelve
\(y^3+xy^2+y+(x^3+x^2y+x)y'=0\) hallando un factor integrante que solo depende del producto \(xy\).
Resuelve estas ecuaciones hallando un factor integrante \(\mu(x,y)=x^{m}y^{n}\)
\[ (1) \quad \left( 4xy+3y^{4}\right) +\left( 2x^{2}+5xy^{3}\right) y'=0 \qquad (2) \quad \left( 2y^2+4x^2y\right) +\left( 4xy+3x^{3}\right) y'=0. \]
{
Aunque existen aportaciones anteriores, el primer matem'atico que parece haber estudiado de manera sistem'atica las integrales de línea del tipo \(\int_C P\, dx+Q\, dy+ R\, dz\) fue Alexis Clairaut. En una serie de trabajos publicados a partir de 1740 dio la primera formulaci'on de las condiciones para que un campo \((P,Q)\) derivase de un potencial (en la nomenclatura de la 'epoca, que la {} $ P dx +Q dy $ fuera {}). Sin embargo, su prueba de que los campos irrotacionales son conservativos no era correcta, lo que fue puesto de mani-fies-to por Jean D’Alembert en 1768 con el mismo ejemplo que hemos visto aquí. Asimismo, Clairaut fue, a partir de trabajos previos de Leonhard Euler, el primero en estudiar las ecuaciones diferenciales exactas y la existencia de factores integrantes. Tras los trabajos de Clairaut, el desarrollo de las integrales de línea tal como lo hemos visto fue establecido por Joseph Louis Lagrange, Pierre S.~Laplace, Carl F.~Gauss, Augustin L.~Cauchy y Bernhard Riemann, a finales del siglo {xviii} y comienzos del {xix}.
%%%%%%%%%%%%%%% El teorema de Green se suele atribuir a G.~Green ya que puede deducirse de otro resultado de su estudio de la teorá del potencial (1828), aunque, de hecho, habá aparecido ya en trabajos de C.F.~Gauss y J.L.~Lagrange. La primera formulaci'on tal y como se usa hoy en dá se debe a A.L.~Cauchy (1846) y la primera demostraci'on rigurosa se debe a B.~Riemann (1851).
Fue Bernard Bolzano el primero en conjeturar de manera precisa que toda curva de Jordan regular a trozos descompone el plano en dos conjuntos conexos y disjuntos que tienen a la curva \(C\) como frontera com'un y en afirmar que no es un resultado evidente, sino que requiere una demostraci'on. La primera demostraci'on se debe al propio Camille Jordan en 1887, pero dicha demostraci'on ha estado sujeta a controversias sobre su completitud, aunque la idea central se considera correcta. Hoy en dá se acepta que la primera prueba completa fue dada por Oswald Veblen en 1905. %%%%%%%%%%%%%%%%%
G.L.~Bradley y K.J.~Smith C{'a}lculo, vol.~2 Capítulo 14
R.E.~Larson, R.P.~Hostetler y B.H.~Edwards C{'a}lculo, vol.~2 Capítulo 14
G.B.~Thomas, Jr. C'alculo, varias variables Secciones 16.1 a 16.3
}
%%%%%%%%%%%%%%%%GREEN
El teorema de Green establece la igualdad, bajo ciertas condiciones, entre una integral doble y una integral de línea en el plano, concretamente
\[ \oint_{C} P\, dx \,+\, Q \,dy = \iint_D \left(\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}\right) \,dx\,dy, \] donde \(D\) es una regi'on acotada del plano y \(C\) es la curva cerrada que forma su frontera.
En cierto modo es un an'alogo bidimensional a la regla de Barrow que, al fin y al cabo, nos dice que podemos calcular la integral de una funci'on en un intervalo \([a,b]\) evaluando una primitiva en la frontera del intervalo: los extremos \(a\) y \(b\).
Para la validez de la igualdad se necesitan dos tipos de hip'otesis. En primer lugar, hip'otesis sobre \(P\) y \(Q\) que garanticen la existencia de las integrales
que aparecen. Habitualmente se considera que \(P\) y \(Q\) son de clase \(C^1\). En segundo lugar hay que imponer condi-cio-nes de tipo geom'etrico sobre el recinto \(D\) y su curva frontera \(C\), concretamente supondremos que \(C\) es una curva de Jordan (o sea, cerrada y simple) regular a trozos. Puede demostrarse (y no es nada elemental aunque sea intuitivamente muy claro) que toda curva de Jordan regular a trozos descompone el plano en dos conjuntos conexos y disjuntos que tienen a la curva \(C\) como frontera com'un. Uno de dichos conjuntos no es acotado y se llama {} El otro sí es acotado y se llama {} esta región interior junto con su frontera \(C\) ser{'a} la región acotada cuya frontera es \(C\) y que representaremos por \(D\).
Finalmente, hay otro detalle que debemos tener en cuenta en el enunciado del teorema de Green, la orientaci'on de la curva \(C\) debe ser la {} es decir, \(C\) debe ser recorrida en sentido contrario a las agujas del reloj, como viste en la asignatura de {Matem'aticas~II}. Esto quiere decir que la parametrizaci'on considerada debe recorrer la curva dejando a la izquierda la región interior. %Nos conformaremos con esta formulaci'on intuitiva.
Sea $C $ una curva de Jordan regular a trozos parametrizada por una función que la recorre en sentido positivo. Sean $ P $ y $ Q$ dos campos escalares de clase \(C^1\) en la región acotada \(D\) cuya frontera es \(C\). Entonces se tiene
\[ \oint_{C} P\, dx \,+\, Q \,dy = \iint_D \left(\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}\right) \,dx\,dy. \] En otros t'erminos, si \(\vector F=(P,Q)\) es de clase \(C^1\) en \(D\), entonces
\[ \oint_C \vector F \cdot \vector r = \iint_D \rot(\vector F)\, dA. \]
Si aplicamos el teorema de Green al campo dado por \(\vector F(x,y)=(-y,x)\), obtenemos una f'ormula para hallar el 'area de la regi'on \(D\).
Sea $C $ una curva de Jordan regular a trozos y sea \(D\) la región acotada cuya frontera es \(C\). Entonces se tiene que
\[ \text{{\'a}rea}(D)=\frac12 \oint_C \bigl( x \,dy\,-\,y\,dx \bigr). \] Esta forma de calcular el 'area de una regi'on a partir de los valores que toma el campo \((-y,x)\) en su frontera es la base te'orica de los {} que son aparatos que permiten calcular el 'area de una regi'on irregular dibujada en un mapa deslizando un puntero por su frontera (mira, por ejemplo, {http://www.youtube.com/watch?v=QA8mOW7fvio}.)
Vamos a usar ahora el teorema de Green para ver que, como anunciamos al final de la secci'on anterior, en el plano hay una clase m'as amplia que la de los conjuntos convexos en los que la irrotacionalidad de un campo garantiza que es conservativo en dicho conjunto.
Se dice que un conjunto \(U\subset \R^2\) es {} si para toda curva de Jordan $ C$ contenida en \(U\), la región acotada \(D\) cuya frontera es \(C\) verifica \(D \subset U\). Gr'aficamente, un conjunto simplemente conexo es un conjunto que no tiene agujeros. Se dice que un conjunto es {} si es conexo pero no es simplemente conexo.
Sea ${F}=(P,Q) $ un campo vectorial de clase \(C^1\) en un conjunto simplemente conexo \(U\subset\R^2\). Se verifica que \({\vector F}\) es conservativo en \(U\) si, y solo si, se cumple $ = $ en \(U\).
Como hemos visto, una región m{'u}ltiplemente conexa es una región con agujeros. Si queremos extender el teorema de Green para este tipo de regiones, a la integral de línea sobre la frontera exterior que aparece debemos a{~n}adir integrales a lo largo de curvas que aíslen los agujeros. Por simplicidad, enunciaremos el teorema para el caso de un recinto con dos agujeros (como la regi'on \(V\) de la figura anterior).
Sea $U^2 $ un conjunto conexo con dos agujeros cuya frontera exterior es una curva de Jordan regular a trozos \(C\). Sean \(C_1\) y \(C_2\) dos curvas de Jordan, regulares a trozos, interiores a \(C\) y exteriores entre sí que rodean los agujeros interiores de \(U\). Sean $ P $ y $ Q$ dos campos escalares de clase \(C^1\) en \(U\). Sea \(D\) la región contenida en \(U\) que es interior a \(C\) y exterior a \(C_1\) y a \(C_2\). Entonces se verifica
\[ \iint_D \left(\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}\right)\, dA = \oint_{C} (P\,dx \,+\, Q\,dy) - \oint_{C_1} (P\,dx \,+ \,Q\,dy)- \oint_{C_2} (P\,dx \,+ \,Q\,dy). \] donde las tres curvas \(C\), \(C_1\) y $C_2 $ son recorridas en sentido positivo.
Sean \(P\) y \(Q\) dos campos escalares de clase \(C^1\) en un conjunto conexo \(U\subset\R^2\) tales que
\(\dfrac{\partial Q}{\partial x}=\dfrac{\partial P}{\partial y}\) en \(U\). Sean \(C_1\) y \(C_2\) dos curvas de Jordan regulares a trozos, contenidas en \(U\), que no se cortan y tales que \(C_1\) rodea completamente a \(C_2\). Supongamos que la región anular \(D\) comprendida entre \(C_1\) y \(C_2\) se queda contenida en \(U\). Entonces se tiene
\[ \oint_{C_1} P\,dx\,+\,Q\,dy=\oint_{C_2} P\,dx\,+\, Q\,dy \] si ambas se recorren en el mismo sentido.
El teorema de Green admite varias interpretaciones y tiene varias consecuencias que afectan a diferentes maneras de considerar las derivadas de los campos vectoriales. Este conjunto de interpre-ta-ciones y fórmulas se conoce como {} y son de mucha utilidad en las aplicaciones al estudio de los campos electromagn'eticos.
Sea ${F}= (P,Q) U ^2 $ un campo vectorial de clase \(C^1(U)\) y sea \(C\) una curva de Jordan regular cuya región interior \(D\) se queda contenida en \(U\) (de manera que podamos aplicar el teorema de Green). Sea \(\vector r(t)=\bigl(x(t),y(t)\bigr)\), para \(t\in [a,b]\), una parametrización de \(C\) que la recorre en sentido positivo. Para cada punto \(P=\bigl(x(t),y(t)\bigr)\) de la curva consideremos su vector tangente unitario \({\vector T}(P)\) y su vector normal exterior unitario \({\vector N}(P)\) dados, respectivamente, por
\[ {\vector T}(P)= \frac{\bigl(x'(t),y'(t) \bigr)}{\norm{\bigl (x'(t),y'(t) \bigr)}} \qquad \text{y} \qquad {\vector N}(P)= \frac{ \bigl(y'(t),-x'(t) \bigr)}{\norm{\bigl(x'(t),y'(t) \bigr)}} \] ({} es porque apunta en direcci'on a la regi'on exterior a \(C\)). Entonces se verifican:
{} La forma de Stokes, o del rotacional, del teorema de Green:
\[ \iint_D \rot(\vector F) \, dx \, dy =\iint_D \left(\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}\right) \, dA = \oint_C P\,dx\,+\,Q\,dy = \oint_{C} {\vector F} \cdot {\vector T} \,ds. \]
El nombre de forma del rotacional se debe a que para un campo bidimensional \({\vector F}= (P,Q)\) su rotacional es \(\rot(\vector F)=\dfrac{\partial Q}{\partial x} - \dfrac{\partial P}{\partial y}\) con lo que la igualdad anterior se puede escribir
\[ \iint_D \rot(\vector F) \, dx \, dy = \oint_C P\,dx\,+\,Q\,dy . \]
{} La forma de Gauss, o de la divergencia, del teorema de Green:
\[ \iint_D \diver(\vector F) \, dx \, dy = \iint_D\left(\frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y}\right) \, dA = \oint_C (-Q)\,dx\,+\,P\,dy = \oint_{C} {\vector F} \cdot {\vector N} \, ds. \] El nombre de forma de la divergencia se debe a que, como veremos en la Lecci'on 6, la divergencia del campo bidimensional \({\vector F}= (P,Q)\) es el campo escalar \(\diver(\vector F)=\dfrac{\partial P}{\partial x} + \dfrac{\partial Q}{\partial y}\).
con lo que la igualdad anterior se puede escribir
\[ \iint_D \diver(\vector F) \, dx \, dy = \oint_C (-Q)\,dx\,+\,P\,dy . \]
Si \(f\) es un campo escalar de clase \(C^1\) en \(U\) se definen su {} \(\dtf\) y su {} \(\dnf\) en un punto de la curva como, respectivamente, las derivadas direccionales con respecto a los vectores unitarios tangente y normal exterior; es decir $ =f $ y $ :=f . $
En las condiciones dadas, sean \(f \colon U \to \R\) un campo escalar y \({\vector F}\colon U \to \R^2\) un campo vectorial, ambos de clase \(C^1\) en \(U\). Entonces
\[ \iint_D f\, \diver({\vector F}) \,dA= \oint_C f \, {\vector F} \cdot {\vector N} \,ds - \iint_D {\vector F} \cdot \nabla f \,dA. \] }
En las condiciones dadas, sean \(f, g \colon U \to \R\) dos campos escalares de clase \(C^2\) en \(U\). Entonces
\[ \align \iint_D f \frac{\partial g}{\partial y} \,dxdy & = -\oint_C f g \,dx - \iint_D g \frac{\partial f}{\partial y} \,dxdy,\\ \iint_D f \frac{\partial g}{\partial x} \,dxdy & = \oint_C f g \,dy - \iint_D g \frac{\partial f}{\partial x} \,dxdy,\\ \iint_D g \nabla^2f \,dxdy & = \oint_C g \dnf \,ds - \iint_D \nabla g \cdot \nabla f \,dxdy,\\ \iint_D (f \nabla^2g-g \nabla^2f) \,dxdy & = \oint_C \left( f \dng -g \dnf \right)\,ds,\\ \iint_D \nabla^2 f \,dxdy & = \oint \dnf \,ds. \endalign \] }
Comprueba la igualdad que establece el teorema de Green para la circunferencia unidad y el campo \({\vector F}(x,y)=(x,2x)\)
Calcula la circulaci'on del campo vectorial \({\vector F}(x,y)=(x+3y, x-y)\) alrededor del tri'angulo de v'ertices \((0,0)\), \((2,0)\) y \((1,4)\).
Sea \(C\) la elipse de ecuación \(\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2}=1\). Sea \({\vector F}(x,y)=(-y,x)\). Comprueba, para la curva \(C\) y el campo \({\vector F}\), la igualdad dada por el teorema de Green.
Sea \(C\) la frontera del cuarto de anillo contenido en el primer cuadrante y comprendido entre las circunferencias de centro el origen y radios 1 y 2, respectivamente. Comprueba, para la curva \(C\) y el campo \({\vector F}(x,y)=(x^2+y^2-y, 2xy)\), la igualdad que establece el teorema de Green.
Usando el teorema de Green, calcula la siguiente integral de línea en el arco de la lemniscata \(C\) dada por la ecuación polar \(r^{2}=a^{2}\cos (2\theta)\), con \(\theta\in [0,{\pi }/{4}]\).
\[ \int_{C}\left( e^{x}\cos (y)+xy^{2}\right) \,dx- \left( e^{x}\sen(y)+x^{2}y\right) \,dy. \]
Sea \(D\) la regi'on limitada inferiormente por la circunferencia unidad y superiormente por la elipse \(4x^2+y^2=4\) y \(C\) su frontera. Consideremos el campo vectorial
\[ {\vector F}(x,y)= \bigl(\cos(2xy)-2xy\sen(2xy)+2xye^{x^2y}, -2x^2\sen(2xy)+x^2e^{x^2y}\bigr). \]
?`Es \({\vector F}\) conservativo en \(\R^2\)? En caso afirmativo, calcula una funci'on potencial. Dado \({\vector G}(x,y)=(x^2+y^2+1,y)\), calcula directamente la integral \(\oint_C({\vector F}+\vector{G})\cdot d{\vector r}\).
Comprueba el resultado del apartado anterior usando el teorema de Green.
Comprueba que se da la igualdad dada por el teorema de Green en los siguientes casos. \({\vector F}(x,y)=(x,1)\), en el cuadrado de vértices \((0,0)\), \((1,0)\), \((1,1)\) y \((0,1)\). \({\vector F}(x,y)=(2xy-x^{2},x+y^{2})\), en el rect{'a}ngulo de vértices \((0,0)\), \((0,2)\), \((1,2)\) y \((1,0)\).
\({\vector F}(x,y)=(x^{2}+y^{2})^{-1}(-y,x)\), en el anillo \(0<a^{2} \leq x^{2}+y^{2}\leq b^{2}\).
Sea \(D\) el semianillo que est'a contenido en el semiplano superior entre la circunferencia \(x^2+y^2=1\) y la circunferencia \(x^2+y^2=4\). Sea \(C\) la frontera del semianillo \(D\). Calcula $ _C y^2 ,dx , + , 3xy , dy$ donde \(C\) se recorre en sentido positivo.
Sea \({\vector F}\) el campo definido para \((x,y)\neq (0,0)\) por $ {F}(x,y)=( , ). $
Prueba que \(\rot({\vector F})=0\) en su dominio de definici'on \(U\). ?`Se puede deducir de este resultado que \({\vector F}\) es conservativo en \(U\)? Explica por qu'e.
Calcula una funci'on potencial de \({\vector F}\) en \(U\). ?`Se puede deducir de la existencia del potencial que \({\vector F}\) es conservativo en \(U\)? Explica por qu'e.
Calcula $ _C F dr$ siendo \(C\) el segmento rectilíneo que va desde \(A=(3,4)\) hasta \(B=(0,2)\).
Consideremos ahora el campo \({\vector G}\) definido para \((x,y)\neq (0,0)\) por \({\vector G}(x,y)= {\vector F}(x,y)+(x,2x)\) y sea \(C_R\) la circunferencia con centro el origen y radio \(R>0\).
Calcula $ _{C_R} G dr$ donde la circunferencia se recorre en sentido positivo.
Sea \(D\) el anillo comprendido entre dos circunferencias \(C_r\) y \(C_R\), definidas como antes, con \(0 < r < R\). Calcula $ _D (G) ,dxdy$ directamente y usando el teorema de Green.
- Prueba que el campo \({\vector F}(x,y)=(3x^2y+3, x^3+2y+2)\) es conservativo en \(\R^2\) y halla una funci'on potencial \(f\) tal que \(f(1,-1)=3\).
Calcula la integral de línea $ _{C_1} F dr, $ siendo \(C_1\) el arco de la curva de ecuaci'on \(y=x^3\) recorrido desde el punto \((0,0)\) hasta el punto \((1,1)\).
Considera ahora el campo $ G(x,y)=( ,, ) $ y calcula el rotacional de \(\vector F + \vector G\). ?`Puedes decir, a partir del valor del rotacional, si \(\vector F + \vector G\) un campo conservativo en su dominio de definici'on?
Sea \(C_2\) la cardioide definida en coordenadas polares por \(r=1+\cos(\theta)\) para \(0 \leq \theta \leq 2\pi\). Calcula $ _{C_2} ( F + G ) dr$ cuando \(C_2\) se recorre en sentido positivo.
Sea \(C\) una curva de Jordan, con regi'on interior \(D\) y sea \(f\) un campo escalar de clase \(C^{2}(U)\) en un dominio \(U\) en el que est'an contenidos \(C\) y \(D\). Prueba que
\[ \oint_{C}\nabla f\cdot {\vector N}\,ds= \iint_{D} \nabla^2 f \,dxdy \] donde \({\vector N}\) es el campo de vectores normales unitarios exteriores a \(C\) y \(\nabla^2 f\) es el laplaciano de \(f\).
Calculando ambas integrales, comprueba que se verifica la igualdad dada antes en el caso particular en que \(C\) es la circunferencia unidad y \(f(x,y)=x^{3}+x^{2}+y^{2}\).
Dado el campo vectorial $F=(, , ).
- Prueba que es irrotacional en su dominio de definici'on.
- Calcula la circulaci'on de \(\vector F\) sobre la circunferencia \(C_a\) con centro el origen y radio \(a \neq 2\).
- ?`Cu'ales son los dominios conexos m'as grandes en los que puedes garantizar que \(\vector F\) es conservativo?
El teorema de Green establece la igualdad, bajo ciertas condiciones, entre una integral doble y una integral de línea en el plano, concretamente [ _{C} P, dx ,+, Q ,dy = _D ( - ) ,dx,dy,] donde (D) es una regi'on acotada del plano y (C) es la curva cerrada que forma su frontera.
En cierto modo es un an'alogo bidimensional a la regla de Barrow que, al fin y al cabo, nos dice que podemos calcular la integral de una funci'on en un intervalo ([a,b]) evaluando una primitiva en la frontera del intervalo: los extremos (a) y (b).
Para la validez de la igualdad se necesitan dos tipos de hip'otesis. En primer lugar, hip'otesis sobre \(P\) y \(Q\) que garanticen la existencia de las integrales
que aparecen. Habitualmente se considera que \(P\) y \(Q\) son de clase \(C^1\). En segundo lugar hay que imponer condi-cio-nes de tipo geom'etrico sobre el recinto \(D\) y su curva frontera \(C\), concretamente supondremos que \(C\) es una curva de Jordan (o sea, cerrada y simple) regular a trozos. Puede demostrarse (y no es nada elemental aunque sea intuitivamente muy claro) que toda curva de Jordan regular a trozos descompone el plano en dos conjuntos conexos y disjuntos que tienen a la curva \(C\) como frontera com'un. Uno de dichos conjuntos no es acotado y se llama {} El otro sí es acotado y se llama {} esta región interior junto con su frontera \(C\) ser{'a} la región acotada cuya frontera es \(C\) y que representaremos por \(D\).
Finalmente, hay otro detalle que debemos tener en cuenta en el enunciado del teorema de Green, la orientaci'on de la curva \(C\) debe ser la {} es decir, \(C\) debe ser recorrida en sentido contrario a las agujas del reloj, como viste en la asignatura de {Matem'aticas~II}. Esto quiere decir que la parametrizaci'on considerada debe recorrer la curva dejando a la izquierda la región interior. %Nos conformaremos con esta formulaci'on intuitiva.
Sea $C $ una curva de Jordan regular a trozos parametrizada por una función que la recorre en sentido positivo. Sean $ P $ y $ Q$ dos campos escalares de clase \(C^1\) en la región acotada \(D\) cuya frontera es \(C\). Entonces se tiene
\[ \oint_{C} P\, dx \,+\, Q \,dy = \iint_D \left(\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}\right) \,dx\,dy. \] En otros t'erminos, si \(\vector F=(P,Q)\) es de clase \(C^1\) en \(D\), entonces
\[ \oint_C \vector F \cdot \vector r = \iint_D \rot(\vector F)\, dA. \]
Si aplicamos el teorema de Green al campo dado por \(\vector F(x,y)=(-y,x)\), obtenemos una f'ormula para hallar el 'area de la regi'on \(D\).
Sea $C $ una curva de Jordan regular a trozos y sea \(D\) la región acotada cuya frontera es \(C\). Entonces se tiene que
\[ \text{{\'a}rea}(D)=\frac12 \oint_C \bigl( x \,dy\,-\,y\,dx \bigr). \] Esta forma de calcular el 'area de una regi'on a partir de los valores que toma el campo \((-y,x)\) en su frontera es la base te'orica de los {} que son aparatos que permiten calcular el 'area de una regi'on irregular dibujada en un mapa deslizando un puntero por su frontera (mira, por ejemplo, {http://www.youtube.com/watch?v=QA8mOW7fvio}.)
Vamos a usar ahora el teorema de Green para ver que, como anunciamos al final de la secci'on anterior, en el plano hay una clase m'as amplia que la de los conjuntos convexos en los que la irrotacionalidad de un campo garantiza que es conservativo en dicho conjunto.
Se dice que un conjunto \(U\subset \R^2\) es {} si para toda curva de Jordan $ C$ contenida en \(U\), la región acotada \(D\) cuya frontera es \(C\) verifica \(D \subset U\). Gr'aficamente, un conjunto simplemente conexo es un conjunto que no tiene agujeros. Se dice que un conjunto es {} si es conexo pero no es simplemente conexo.
Sea ${F}=(P,Q) $ un campo vectorial de clase \(C^1\) en un conjunto simplemente conexo \(U\subset\R^2\). Se verifica que \({\vector F}\) es conservativo en \(U\) si, y solo si, se cumple $ = $ en \(U\).
Como hemos visto, una región m{'u}ltiplemente conexa es una región con agujeros. Si queremos extender el teorema de Green para este tipo de regiones, a la integral de línea sobre la frontera exterior que aparece debemos a{~n}adir integrales a lo largo de curvas que aíslen los agujeros. Por simplicidad, enunciaremos el teorema para el caso de un recinto con dos agujeros (como la regi'on \(V\) de la figura anterior).
Sea $U^2 $ un conjunto conexo con dos agujeros cuya frontera exterior es una curva de Jordan regular a trozos \(C\). Sean \(C_1\) y \(C_2\) dos curvas de Jordan, regulares a trozos, interiores a \(C\) y exteriores entre sí que rodean los agujeros interiores de \(U\). Sean $ P $ y $ Q$ dos campos escalares de clase \(C^1\) en \(U\). Sea \(D\) la región contenida en \(U\) que es interior a \(C\) y exterior a \(C_1\) y a \(C_2\). Entonces se verifica
\[ \iint_D \left(\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}\right)\, dA = \oint_{C} (P\,dx \,+\, Q\,dy) - \oint_{C_1} (P\,dx \,+ \,Q\,dy)- \oint_{C_2} (P\,dx \,+ \,Q\,dy). \] donde las tres curvas \(C\), \(C_1\) y $C_2 $ son recorridas en sentido positivo.
Sean \(P\) y \(Q\) dos campos escalares de clase \(C^1\) en un conjunto conexo \(U\subset\R^2\) tales que
\(\dfrac{\partial Q}{\partial x}=\dfrac{\partial P}{\partial y}\) en \(U\). Sean \(C_1\) y \(C_2\) dos curvas de Jordan regulares a trozos, contenidas en \(U\), que no se cortan y tales que \(C_1\) rodea completamente a \(C_2\). Supongamos que la región anular \(D\) comprendida entre \(C_1\) y \(C_2\) se queda contenida en \(U\). Entonces se tiene
\[ \oint_{C_1} P\,dx\,+\,Q\,dy=\oint_{C_2} P\,dx\,+\, Q\,dy \] si ambas se recorren en el mismo sentido.
El teorema de Green admite varias interpretaciones y tiene varias consecuencias que afectan a diferentes maneras de considerar las derivadas de los campos vectoriales. Este conjunto de interpre-ta-ciones y fórmulas se conoce como {} y son de mucha utilidad en las aplicaciones al estudio de los campos electromagn'eticos.
Sea ${F}= (P,Q) U ^2 $ un campo vectorial de clase \(C^1(U)\) y sea \(C\) una curva de Jordan regular cuya región interior \(D\) se queda contenida en \(U\) (de manera que podamos aplicar el teorema de Green). Sea \(\vector r(t)=\bigl(x(t),y(t)\bigr)\), para \(t\in [a,b]\), una parametrización de \(C\) que la recorre en sentido positivo. Para cada punto \(P=\bigl(x(t),y(t)\bigr)\) de la curva consideremos su vector tangente unitario \({\vector T}(P)\) y su vector normal exterior unitario \({\vector N}(P)\) dados, respectivamente, por
\[ {\vector T}(P)= \frac{\bigl(x'(t),y'(t) \bigr)}{\norm{\bigl (x'(t),y'(t) \bigr)}} \qquad \text{y} \qquad {\vector N}(P)= \frac{ \bigl(y'(t),-x'(t) \bigr)}{\norm{\bigl(x'(t),y'(t) \bigr)}} \] ({} es porque apunta en direcci'on a la regi'on exterior a \(C\)). Entonces se verifican:
{} La forma de Stokes, o del rotacional, del teorema de Green:
\[ \iint_D \rot(\vector F) \, dx \, dy =\iint_D \left(\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}\right) \, dA = \oint_C P\,dx\,+\,Q\,dy = \oint_{C} {\vector F} \cdot {\vector T} \,ds. \]
El nombre de forma del rotacional se debe a que para un campo bidimensional \({\vector F}= (P,Q)\) su rotacional es \(\rot(\vector F)=\dfrac{\partial Q}{\partial x} - \dfrac{\partial P}{\partial y}\) con lo que la igualdad anterior se puede escribir
\[ \iint_D \rot(\vector F) \, dx \, dy = \oint_C P\,dx\,+\,Q\,dy . \]
{} La forma de Gauss, o de la divergencia, del teorema de Green:
\[ \iint_D \diver(\vector F) \, dx \, dy = \iint_D\left(\frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y}\right) \, dA = \oint_C (-Q)\,dx\,+\,P\,dy = \oint_{C} {\vector F} \cdot {\vector N} \, ds. \] El nombre de forma de la divergencia se debe a que, como veremos en la Lecci'on 6, la divergencia del campo bidimensional \({\vector F}= (P,Q)\) es el campo escalar \(\diver(\vector F)=\dfrac{\partial P}{\partial x} + \dfrac{\partial Q}{\partial y}\).
con lo que la igualdad anterior se puede escribir
\[ \iint_D \diver(\vector F) \, dx \, dy = \oint_C (-Q)\,dx\,+\,P\,dy . \]
Si \(f\) es un campo escalar de clase \(C^1\) en \(U\) se definen su {} \(\dtf\) y su {} \(\dnf\) en un punto de la curva como, respectivamente, las derivadas direccionales con respecto a los vectores unitarios tangente y normal exterior; es decir $ =f $ y $ :=f . $
En las condiciones dadas, sean \(f \colon U \to \R\) un campo escalar y \({\vector F}\colon U \to \R^2\) un campo vectorial, ambos de clase \(C^1\) en \(U\). Entonces
\[ \iint_D f\, \diver({\vector F}) \,dA= \oint_C f \, {\vector F} \cdot {\vector N} \,ds - \iint_D {\vector F} \cdot \nabla f \,dA. \] }
En las condiciones dadas, sean \(f, g \colon U \to \R\) dos campos escalares de clase \(C^2\) en \(U\). Entonces
\[ \align \iint_D f \frac{\partial g}{\partial y} \,dxdy & = -\oint_C f g \,dx - \iint_D g \frac{\partial f}{\partial y} \,dxdy,\\ \iint_D f \frac{\partial g}{\partial x} \,dxdy & = \oint_C f g \,dy - \iint_D g \frac{\partial f}{\partial x} \,dxdy,\\ \iint_D g \nabla^2f \,dxdy & = \oint_C g \dnf \,ds - \iint_D \nabla g \cdot \nabla f \,dxdy,\\ \iint_D (f \nabla^2g-g \nabla^2f) \,dxdy & = \oint_C \left( f \dng -g \dnf \right)\,ds,\\ \iint_D \nabla^2 f \,dxdy & = \oint \dnf \,ds. \endalign \] }
Comprueba la igualdad que establece el teorema de Green para la circunferencia unidad y el campo \({\vector F}(x,y)=(x,2x)\)
Calcula la circulaci'on del campo vectorial \({\vector F}(x,y)=(x+3y, x-y)\) alrededor del tri'angulo de v'ertices \((0,0)\), \((2,0)\) y \((1,4)\).
Sea \(C\) la elipse de ecuación \(\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2}=1\). Sea \({\vector F}(x,y)=(-y,x)\). Comprueba, para la curva \(C\) y el campo \({\vector F}\), la igualdad dada por el teorema de Green.
Sea \(C\) la frontera del cuarto de anillo contenido en el primer cuadrante y comprendido entre las circunferencias de centro el origen y radios 1 y 2, respectivamente. Comprueba, para la curva \(C\) y el campo \({\vector F}(x,y)=(x^2+y^2-y, 2xy)\), la igualdad que establece el teorema de Green.
Usando el teorema de Green, calcula la siguiente integral de línea en el arco de la lemniscata \(C\) dada por la ecuación polar \(r^{2}=a^{2}\cos (2\theta)\), con \(\theta\in [0,{\pi }/{4}]\).
\[ \int_{C}\left( e^{x}\cos (y)+xy^{2}\right) \,dx- \left( e^{x}\sen(y)+x^{2}y\right) \,dy. \]
Sea \(D\) la regi'on limitada inferiormente por la circunferencia unidad y superiormente por la elipse \(4x^2+y^2=4\) y \(C\) su frontera. Consideremos el campo vectorial
\[ {\vector F}(x,y)= \bigl(\cos(2xy)-2xy\sen(2xy)+2xye^{x^2y}, -2x^2\sen(2xy)+x^2e^{x^2y}\bigr). \]
?`Es \({\vector F}\) conservativo en \(\R^2\)? En caso afirmativo, calcula una funci'on potencial. Dado \({\vector G}(x,y)=(x^2+y^2+1,y)\), calcula directamente la integral \(\oint_C({\vector F}+\vector{G})\cdot d{\vector r}\).
Comprueba el resultado del apartado anterior usando el teorema de Green.
Comprueba que se da la igualdad dada por el teorema de Green en los siguientes casos. \({\vector F}(x,y)=(x,1)\), en el cuadrado de vértices \((0,0)\), \((1,0)\), \((1,1)\) y \((0,1)\). \({\vector F}(x,y)=(2xy-x^{2},x+y^{2})\), en el rect{'a}ngulo de vértices \((0,0)\), \((0,2)\), \((1,2)\) y \((1,0)\).
\({\vector F}(x,y)=(x^{2}+y^{2})^{-1}(-y,x)\), en el anillo \(0<a^{2} \leq x^{2}+y^{2}\leq b^{2}\).
Sea \(D\) el semianillo que est'a contenido en el semiplano superior entre la circunferencia \(x^2+y^2=1\) y la circunferencia \(x^2+y^2=4\). Sea \(C\) la frontera del semianillo \(D\). Calcula $ _C y^2 ,dx , + , 3xy , dy$ donde \(C\) se recorre en sentido positivo.
Sea \({\vector F}\) el campo definido para \((x,y)\neq (0,0)\) por $ {F}(x,y)=( , ). $
Prueba que \(\rot({\vector F})=0\) en su dominio de definici'on \(U\). ?`Se puede deducir de este resultado que \({\vector F}\) es conservativo en \(U\)? Explica por qu'e.
Calcula una funci'on potencial de \({\vector F}\) en \(U\). ?`Se puede deducir de la existencia del potencial que \({\vector F}\) es conservativo en \(U\)? Explica por qu'e.
Calcula $ _C F dr$ siendo \(C\) el segmento rectilíneo que va desde \(A=(3,4)\) hasta \(B=(0,2)\).
Consideremos ahora el campo \({\vector G}\) definido para \((x,y)\neq (0,0)\) por \({\vector G}(x,y)= {\vector F}(x,y)+(x,2x)\) y sea \(C_R\) la circunferencia con centro el origen y radio \(R>0\).
Calcula $ _{C_R} G dr$ donde la circunferencia se recorre en sentido positivo.
Sea \(D\) el anillo comprendido entre dos circunferencias \(C_r\) y \(C_R\), definidas como antes, con \(0 < r < R\). Calcula $ _D (G) ,dxdy$ directamente y usando el teorema de Green.
- Prueba que el campo \({\vector F}(x,y)=(3x^2y+3, x^3+2y+2)\) es conservativo en \(\R^2\) y halla una funci'on potencial \(f\) tal que \(f(1,-1)=3\).
Calcula la integral de línea $ _{C_1} F dr, $ siendo \(C_1\) el arco de la curva de ecuaci'on \(y=x^3\) recorrido desde el punto \((0,0)\) hasta el punto \((1,1)\).
Considera ahora el campo $ G(x,y)=( ,, ) $ y calcula el rotacional de \(\vector F + \vector G\). ?`Puedes decir, a partir del valor del rotacional, si \(\vector F + \vector G\) un campo conservativo en su dominio de definici'on?
Sea \(C_2\) la cardioide definida en coordenadas polares por \(r=1+\cos(\theta)\) para \(0 \leq \theta \leq 2\pi\). Calcula $ _{C_2} ( F + G ) dr$ cuando \(C_2\) se recorre en sentido positivo.
Sea \(C\) una curva de Jordan, con regi'on interior \(D\) y sea \(f\) un campo escalar de clase \(C^{2}(U)\) en un dominio \(U\) en el que est'an contenidos \(C\) y \(D\). Prueba que
\[ \oint_{C}\nabla f\cdot {\vector N}\,ds= \iint_{D} \nabla^2 f \,dxdy \] donde \({\vector N}\) es el campo de vectores normales unitarios exteriores a \(C\) y \(\nabla^2 f\) es el laplaciano de \(f\).
Calculando ambas integrales, comprueba que se verifica la igualdad dada antes en el caso particular en que \(C\) es la circunferencia unidad y \(f(x,y)=x^{3}+x^{2}+y^{2}\).
Dado el campo vectorial $F=(, , ).
- Prueba que es irrotacional en su dominio de definici'on.
- Calcula la circulaci'on de \(\vector F\) sobre la circunferencia \(C_a\) con centro el origen y radio \(a \neq 2\).
- ?`Cu'ales son los dominios conexos m'as grandes en los que puedes garantizar que \(\vector F\) es conservativo?

