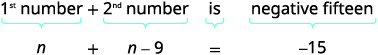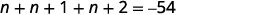2.3: Usar una estrategia de resolución de problemas
- Page ID
- 112745
Al final de esta sección, podrás:
- Usar una estrategia de resolución de problemas para problemas de palabras
- Resolver problemas numéricos
- Resolver porcentaje de aplicaciones
- Resolver aplicaciones de interés simples
Antes de comenzar, toma este cuestionario de preparación.
¿Alguna vez has tenido alguna experiencia negativa en el pasado con problemas de palabras? Cuando sentimos que no tenemos control, y seguimos repitiendo pensamientos negativos, establecemos barreras para el éxito. Date cuenta de que tus experiencias negativas con problemas de palabras están en tu pasado. Para seguir adelante necesitas calmar tus miedos y cambiar tus sentimientos negativos.
Comience con una nueva pizarra y comience a pensar pensamientos positivos. Repitiendo algunas de las siguientes afirmaciones puede ser útil para que tus pensamientos sean positivos. Pensar pensamientos positivos es un primer paso hacia el éxito.
- ¡Creo que puedo! ¡Creo que puedo!
- Si bien los problemas de palabras fueron duros en el pasado, creo que puedo probarlos ahora.
- Ahora estoy mejor preparado, creo que empezaré a entender los problemas de la palabra.
- Soy capaz de resolver ecuaciones porque practiqué muchos problemas y obtuve ayuda cuando la necesitaba, puedo intentarlo con problemas de palabras.
- Puede llevar tiempo, pero puedo empezar a resolver problemas de palabras.
- Ahora estás bien preparado y estás listo para triunfar. Si tomas el control y crees que puedes tener éxito, podrás dominar los problemas de la palabra.
Usar una estrategia de resolución de problemas para problemas de palabras
Ahora que podemos resolver ecuaciones, estamos listos para aplicar nuestras nuevas habilidades a los problemas de la palabra. Desarrollaremos una estrategia que podamos usar para resolver cualquier problema de palabras con éxito.
La nevada anual normal en la estación de esquí local es de 12 pulgadas más del doble de la cantidad que recibió la temporada pasada. La nevada anual normal es de 62 pulgadas. ¿Cuál fue la nevada de la temporada pasada en la estación de esquí?
Solución:
| Paso 1. Lee el problema. | |
| Paso 2. Identifica lo que buscas. | ¿Cuál fue la nevada de la temporada pasada? |
| Paso 3. Nombra lo que estamos buscando y elige una variable para representarlo. | Deja que\(s=\) las nevadas la temporada pasada. |
| Paso 4. Traducir. Reafirmar el problema en una frase con toda la información importante. |  |
| Traducir en una ecuación. |  |
| Paso 5. Resuelve la ecuación. | 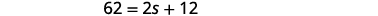 |
| Restar 12 de cada lado. | 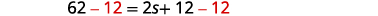 |
| Simplificar. |  |
| Divide cada lado por dos. |  |
| Simplificar. |  |
| Paso 6. Consulta: Primero, ¿nuestra respuesta es razonable? Sí, tener 25 pulgadas de nieve parece estar bien. El problema dice que la nevada normal es de doce pulgadas más del doble del número de la temporada pasada. Dos veces 25 es 50 y 12 más que eso es 62. | |
| Paso 7. Contesta la pregunta. | La nevada de la temporada pasada fue de 25 pulgadas. |
Guillermo compró libros de texto y cuadernos en la librería. El número de libros de texto era tres más del doble del número de cuadernos. Compró siete libros de texto. ¿Cuántos cuadernos compró?
- Contestar
-
Compró dos cuadernos
Gerry trabajó esta semana con puzles de Sudoku y crucigramas. El número de rompecabezas de Sudoku que completó es de ocho más del doble del número de crucigramas. Completó 22 acertijos de Sudoku. ¿Cuántos crucigramas hizo?
- Contestar
-
Él hizo siete crucigramas
Resumimos una estrategia efectiva para la resolución de problemas.
- Lee el problema. Asegúrate de que todas las palabras e ideas sean entendidas.
- Identifica lo que buscas.
- Nombra lo que buscas. Elija una variable para representar esa cantidad.
- Traducir en una ecuación. Puede ser útil reafirmar el problema en una oración con toda la información importante. Después, traducir la oración en inglés a una ecuación álgebra.
- Resolver la ecuación utilizando técnicas de álgebra adecuadas.
- Verifique la respuesta en el problema para asegurarse de que tenga sentido.
- Contesta la pregunta con una oración completa.
Resolver problemas numéricos
Ahora aplicaremos la estrategia de resolución de problemas a los “problemas numéricos de palabras”. Los problemas numéricos dan algunas pistas sobre uno o más números y usamos estas pistas para escribir una ecuación. Los problemas numéricos proporcionan buenas prácticas para usar la Estrategia de Resolución de Problemas.
La suma de siete veces por número y ocho es treinta y seis. Encuentra el número.
Solución:
| Paso 1. Lee el problema. | |
|---|---|
| Paso 2. Identifica lo que buscas. | el número |
|
Paso 3. Nombra lo que buscas y elegir una variable para representarla. |
Deja\(n=\) el número. |
|
Paso 4. Traducir: Reformular el problema como una sola oración. Traducir en una ecuación. |
|
|
Paso 5. Resuelve la ecuación. Restar ocho de cada lado y simplificar. Divide cada lado por siete y simplifica. |
|
|
Paso 6. Cheque. ¿La suma de siete por cuatro más ocho es igual a 36? \[\begin{align*} 7·4+8 & \stackrel{?}{=}36 \\ 28+8 & \stackrel{?}{=}36 \\ 36 & =36✓ \end{align*}\] |
|
| Paso 7. Contesta la pregunta. | El número es 4. |
¿Se dio cuenta de que dejamos fuera algunos de los pasos a medida que resolvimos esta ecuación? Si aún no estás listo para dejar de lado estos pasos, anota tantos como necesites.
La suma de cuatro veces un número y dos es catorce. Encuentra el número.
- Contestar
-
\(3\)
La suma de tres veces un número y siete es veinticinco. Encuentra el número.
- Contestar
-
\(6\)
Algunos problemas de palabras numéricos nos piden encontrar dos o más números. Puede ser tentador nombrarlos a todos con diferentes variables, pero hasta ahora, solo hemos resuelto ecuaciones con una variable. Para evitar el uso de más de una variable, definiremos los números en términos de la misma variable. Asegúrese de leer el problema detenidamente para descubrir cómo todos los números se relacionan entre sí.
La suma de dos números es de quince negativos. Un número es nueve menos que el otro. Encuentra los números.
Solución:
| Paso 1. Lee el problema. | |
| Paso 2. Identifica lo que buscas. | dos números |
| Paso 3. Nombra lo que buscas eligiendo una variable para representar el primer número. “Un número es nueve menos que el otro”. | Vamos\(n=1^{\text{st}}\) número. \(n−9=2^{\text{nd}}\)número |
| Paso 4. Traducir. Escribe como una sola oración. Traducir en una ecuación. | La suma de dos números es de quince negativos.
|
|
Paso 5. Resuelve la ecuación. Combina términos similares. Agrega nueve a cada lado y simplifica. Simplificar. |
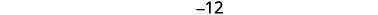 |
| Paso 6. Cheque. ¿\(−12\)Nueve es menos que\(−3\)? \[\begin{align*}−3−9 & \stackrel{?}{=}−12 \\ −12 & =−12✓ \end{align*}\]Es su suma\(−15?\)\[\begin{align*} −3+(−12) & \stackrel{?}{=}−15 \\ −15 & =−15✓ \end{align*}\] | |
| Paso 7. Contesta la pregunta. | Los números son\(−3\) y\(−12\). |
La suma de dos números es negativa veintitrés. Un número es siete menos que el otro. Encuentra los números.
- Contestar
-
\(−15,−8\)
La suma de dos números es negativa dieciocho. Un número es cuarenta más que el otro. Encuentra los números.
- Contestar
-
\(−29,11\)
Algunos problemas numéricos involucran números enteros consecutivos. Los enteros consecutivos son enteros que se suceden inmediatamente entre sí. Ejemplos de números enteros consecutivos son:
\[\begin{array}{rrrr} 1, & 2, & 3, & 4 \\ −10, & −9, & −8, & −7\\ 150, & 151, & 152, & 153 \end{array}\nonumber\]
Observe que cada número es uno más que el número que lo precede. Por lo tanto, si definimos el primer entero como\(n,\) el siguiente entero consecutivo es\(n+1\). El de después de eso es uno más que\(n+1\), así es\(n+1+1\), que es\(n+2\).
\[\begin{array}{ll} n & 1^{\text{st}} \text{integer} \\ n+1 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; & 2^{\text{nd}}\text{consecutive integer} \\ n+2 & 3^{\text{rd}}\text{consecutive integer} \;\;\;\;\;\;\;\; \text{etc.} \end{array}\nonumber\]
Usaremos esta notación para representar enteros consecutivos en el siguiente ejemplo.
Encuentra tres enteros consecutivos cuya suma es\(−54\).
Solución:
| Paso 1. Lee el problema. | |
| Paso 2. Identifica lo que buscas. | tres enteros consecutivos |
| Paso 3. Nombra cada uno de los tres números | Vamos\(n=1^{\text{st}} \text{integer}\). \(n+1=2^{\text{nd}} \text{consecutive integer}\)\(n+2=3^{\text{rd}} \text{consecutive integer}\) |
| Paso 4. Traducir. Reformular como una sola oración. Traducir en una ecuación. | La suma de los tres enteros es\(−54\).
|
| Paso 5. Resuelve la ecuación. Combina términos similares. Restar tres de cada lado. Divide cada lado por tres. | 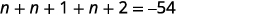 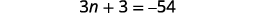 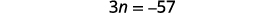 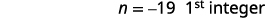
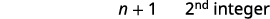 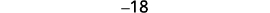 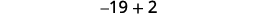 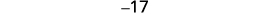 |
| Paso 6. Cheque. \(\begin{align*} −19+(−18)+(−17) & =−54 \\ −54 & =−54✓ \end{align*}\) | |
| Paso 7. Contesta la pregunta. | Los tres números enteros consecutivos son −17, −18 y −19. |
Encuentra tres enteros consecutivos cuya suma es\(−96\).
- Contestar
-
\(−33,−32,−31\)
Encuentra tres enteros consecutivos cuya suma es\(−36\).
- Contestar
-
\(−13,−12,−11\)
Ahora que hemos trabajado con enteros consecutivos, ampliaremos nuestro trabajo para incluir enteros pares consecutivos y enteros impares consecutivos. Los enteros pares consecutivos son enteros pares que inmediatamente se suceden unos a otros. Ejemplos de enteros pares consecutivos son:
\[24, 26, 28\nonumber\]
\[−12,−10,−8\nonumber\]
Observe que cada entero es dos más que el número que lo precede. Si llamamos al primero\(n,\) entonces el siguiente es\(n+2\). El de después de eso sería\(n+2+2\) o\(n+4\).
\[\begin{array}{ll} n & 1^{\text{st}} \text{integer} \\ n+1 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; & 2^{\text{nd}}\text{consecutive integer} \\ n+2 & 3^{\text{rd}}\text{consecutive integer} \;\;\;\;\;\;\;\; \text{etc.} \end{array}\nonumber\]
Los enteros impares consecutivos son enteros impares que se suceden inmediatamente entre sí. Considera los enteros impares consecutivos 63, 65 y 67.
\[63, 65, 67\nonumber\]
\[n,n+2,n+4\nonumber\]
\[\begin{array}{ll} n & 1^{\text{st}} \text{integer} \\ n+1 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; & 2^{\text{nd}}\text{consecutive integer} \\ n+2 & 3^{\text{rd}}\text{consecutive integer} \;\;\;\;\;\;\;\; \text{etc.} \end{array}\nonumber\]
¿Parece extraño tener que sumar dos (un número par) para obtener el siguiente número impar? ¿Obtenemos un número impar o par cuando sumamos 2 a 3? a 11? a 47?
Ya sea que el problema pida números pares consecutivos o números impares, no tienes que hacer nada diferente. El patrón sigue siendo el mismo: para llegar al siguiente impar o al siguiente número entero par, agregue dos.
Encuentra tres enteros pares consecutivos cuya suma es\(120\).
Solución:
| Paso 1. Lee el problema. | |
| Paso 2. Identifica lo que buscas. | tres enteros pares consecutivos |
| Paso 3. Nombra cada uno de los tres números |
Vamos\(n = 1^{\text{st}} \text{consecutive even integer}\). \(n + 2 = 2^{\text{nd}} \text{consecutive even integer}\). \(n + 4 = 3^{\text{rd}} \text{consecutive even integer}\). |
| Paso 4. Traducir.
Reafirmar como una sola oración. Traducir en una ecuación. |
La suma de los tres enteros pares es 120 \(n + n + 2 + n + 4 = 120\) |
| Paso 5. Resuelve la ecuación.
Combina términos similares. Restar tres de cada lado. Divide cada lado por tres. |
\(n + n + 2 + n + 4 = 120\) \(\begin{aligned} &{3n+6=120} \\ &{3n=114} \\ &{n=38} &{1^\text{st} \text{integer}}\end{aligned}\) \(\begin{aligned} &{n+2} & &{2^\text{nd} \text{integer}}\\ &{38+2} \\ &{40} \end{aligned}\) \(\begin{aligned} &{n+2} & &{3^\text{rd} \text{integer}}\\ &{38+4} \\ &{42} \end{aligned}\) |
| Paso 6. Cheque. \(\begin{align*} 38 + 40 + 42 &\overset{?}{=} &120 \nonumber\\ 120 &=& 120 &✓ \nonumber\end{align*}\) | |
| Paso 7. Contesta la pregunta. | Los tres números enteros consecutivos son 38, 40 y 42. |
Encuentra tres enteros pares consecutivos cuya suma sea 102.
- Contestar
-
\(32, 34, 36\)
Encuentra tres enteros pares consecutivos cuya suma es\(−24\).
- Contestar
-
\(−10,−8,−6\)
Cuando un problema numérico está en un contexto de la vida real, seguimos usando las mismas estrategias que usamos para los ejemplos anteriores.
Una pareja casada gana 110 mil dólares al año. La esposa gana $16,000 menos del doble de lo que gana su esposo. ¿Qué gana el marido?
Solución:
| Paso 1. Lee el problema. | |
| Paso 2. Identifica lo que buscas. | ¿Cuánto gana el marido? |
| Paso 3. Nombra cada uno de los tres números |
Vamos\(h=\text{the amount the husband earns}\). |
| Paso 4. Traducir.
Reafirmar el problema en una frase con toda la información importante. Traducir en una ecuación. |
\(2h−16,000=\text{the amount the wife earns}.\)Juntos el esposo y la esposa ganan 110 mil dólares. \(h+2h−16,000=110,000\) |
| Paso 5. Resuelve la ecuación.
Combina términos similares. Agregue 16,000 a ambos lados y simplifique. Divide cada lado por tres. |
\(h+2h−16,000=110,000\) \(\begin{aligned} &{3h−16,000=110,000} \\ &{3h=126,000} \\ &{h=42,000} &{\text{amount husband earns}} \end{aligned}\) \(\begin{aligned} &{2h−16,000} &{\text{ amount wife earns}} \\ &{2(42,000)−16,000} \\ &{84,000−16,000} \\ &{68,000} \end{aligned}\) |
| Paso 6. Cheque. Si la esposa gana 68 mil dólares y el esposo gana 42 mil, ¿son 110 mil dólares? ¡Sí! | |
| Paso 7. Contesta la pregunta. | El esposo gana 42 mil dólares al año. |
Según la Asociación Nacional de Concesionarios de Automóviles, el costo promedio de un automóvil en 2014 fue de 28.400 dólares. Esto fue $1,600 menos que seis veces el costo en 1975. ¿Cuál fue el costo promedio de un automóvil en 1975?
- Contestar
-
El costo promedio fue de $5,000.
Los datos del Censo de Estados Unidos muestran que el precio medio de la vivienda nueva en Estados Unidos en noviembre de 2014 fue de 280,900 dólares. Esto fue de 10.700 dólares más que 14 veces el precio en noviembre de 1964. ¿Cuál era el precio medio de una casa nueva en noviembre de 1964?
- Contestar
-
El precio medio fue de $19,300.
Resolver porcentaje de aplicaciones
Existen varios métodos para resolver ecuaciones porcentuales. En álgebra, es más fácil si solo traducimos oraciones en inglés a ecuaciones algebraicas y luego resolvemos las ecuaciones. Asegúrese de cambiar el porcentaje dado a un decimal antes de usarlo en la ecuación.
Traducir y resolver:
- ¿Qué número es 45% de 84?
- ¿8.5% de qué cantidad es $4.76?
- ¿168 es qué porcentaje de 112?
Solución:
a.
 |
|
| Traducir al álgebra. Dejar n = el número. | 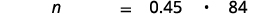 |
| Multiplicar. | 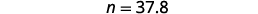 |
| 37.8 es 45% de 84. |
b.
 |
|
| Traducir. Dejar\(n =\) la cantidad. | 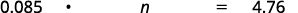 |
| Multiplicar. | 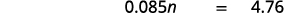 |
| Divide ambos lados por 0.085 y simplifica. |  |
| 8.5% de $56 es $4.76 |
c.
| Se nos pide encontrar por ciento, por lo que debemos tener nuestro resultado en forma de porcentaje. |  |
| Traducir al álgebra. Que\(p = \) el porcentaje. | 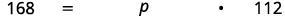 |
| Multiplicar. |  |
| Divide ambos lados por 112 y simplifica. | .jpg) |
| Convertir a porcentaje. |  |
| 168 es 150% de 112. |
Traducir y resolver:
- ¿Qué número es 45% de 80?
- ¿7.5% de qué cantidad es $1.95?
- ¿110 es qué porcentaje de 88?
- Contestar
-
a. 36 b. $26 c.\(125 \% \)
Traducir y resolver:
- ¿Qué número es 55% de 60?
- ¿8.5% de qué cantidad es $3.06?
- ¿126 es qué porcentaje de 72?
- Contestar
-
a. 33 b. $36 c.\(175 \% \)
Ahora que tenemos una estrategia de resolución de problemas a la que referirnos, y hemos practicado la resolución de ecuaciones porcentuales básicas, estamos listos para resolver aplicaciones porcentuales. Asegúrese de preguntarse si su respuesta final tiene sentido, ya que muchas de las aplicaciones que resolveremos involucran situaciones cotidianas, puede confiar en su propia experiencia.
La etiqueta del yogur de Audrey decía que una porción proporcionó 12 gramos de proteína, que es 24% de la cantidad diaria recomendada. ¿Cuál es la cantidad diaria total recomendada de proteína?
Solución:
| ¿Qué se le pide que encuentre? | ¿Qué cantidad total de proteína se recomienda? |
| Elija una variable para representarla. | Dejar cantidad\(a=\) total de proteína. |
| Escribe una frase que dé la información para encontrarla. | 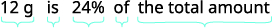 |
| Traducir en una ecuación. |  |
| Resolver. |  |
| Cheque: ¿Tiene sentido esto? Sí, 24% es aproximadamente\(\frac{1}{4}\) del total y 12 es aproximadamente\(\frac{1}{4}\) de 50. | |
| Escribe una oración completa para responder a la pregunta. | La cantidad de proteína que se recomienda es de 50 g. |
Una porción de cereal cuadrado de trigo tiene 7 gramos de fibra, que es 28% de la cantidad diaria recomendada. ¿Cuál es la cantidad diaria total recomendada de fibra?
- Contestar
-
25 gramos
Una porción de cereal de arroz tiene 190 mg de sodio, que es 8% de la cantidad diaria recomendada. ¿Cuál es la cantidad diaria total recomendada de sodio?
- Contestar
-
2,375 mg
Recuerda poner la respuesta en el formulario solicitado. En el siguiente ejemplo estamos buscando el porcentaje.
Verónica planea hacer muffins a partir de una mezcla. El paquete dice que cada muffin será de 240 calorías y 60 calorías serán de grasa. ¿Qué porcentaje del total de calorías proviene de la grasa?
Solución:
| ¿Qué se le pide que encuentre? | ¿Qué porcentaje del total de calorías es grasa? |
| Elija una variable para representarla. | Dejar\(p=\) por ciento de grasa. |
| Escribe una frase que dé la información para encontrarla. |  |
| Traducir la oración en una ecuación. |  |
| Multiplicar. |  |
| Divide ambos lados por 240. |  |
| Poner en forma de porcentaje. |  |
| Cheque: ¿tiene sentido esto? Sí,\(25 \% \) es un cuarto; 60 es un cuarto de 240. Entonces, tiene\(25 \%\) sentido. | |
| Escribe una oración completa para responder a la pregunta. | Del total de calorías en cada muffin,\(25 \%\) es grasa. |
Mitzi recibió unos brownies gourmet como regalo. El envoltorio decía que cada 28% de brownie era de 480 calorías, y tenía 240 calorías de grasa. ¿Qué porcentaje del total de calorías en cada brownie proviene de la grasa? Redondear la respuesta al porcentaje entero más cercano.
- Contestar
-
50%
El mix que Ricardo planea usar para hacer brownies dice que cada brownie será de 190 calorías, y 76 calorías son de grasa. ¿Qué porcentaje de las calorías totales provienen de la grasa? Redondear la respuesta al porcentaje entero más cercano.
- Contestar
-
40%
A menudo es importante en muchos campos —negocios, ciencias, cultura pop— hablar sobre cuánto ha aumentado o disminuido una cantidad durante un cierto período de tiempo. Este incremento o disminución generalmente se expresa como un porcentaje y se denomina cambio porcentual.
Para encontrar el cambio porcentual, primero encontramos la cantidad de cambio, al encontrar la diferencia de la nueva cantidad y la cantidad original. Entonces encontramos qué porcentaje es la cantidad de cambio de la cantidad original.
- Encuentra la cantidad de cambio.
\[\text{change}= \text{new amount}−\text{original amount}\]
- Encuentra qué porcentaje es la cantidad de cambio de la cantidad original.
cambio es ¿qué porcentaje de la cantidad original?
Recientemente, el gobernador de California propuso aumentar las cuotas de los colegios comunitarios de 36 dólares por unidad a 46 dólares por unidad. Encuentra el cambio porcentual. (Redondear a la décima más cercana de un porcentaje.)
Solución:
| Encuentra la cantidad de cambio. | \(46−36=10\) |
| Encuentra el porcentaje. | El cambio es ¿qué porcentaje de la cantidad original? |
| Que\(p=\) el porcentaje. |  |
| Traducir a una ecuación. | 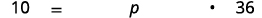 |
| Simplificar. | \(10=36 p\) |
| Divide ambos lados por 36. | \(0.278 \approx p\) |
| Cambiar a forma porcentual; redondear a la décima más cercana | \(27.8 \% \approx p\) |
| Escribe una oración completa para responder a la pregunta. | Las nuevas tarifas son aproximadamente un\(27.8 \% \) aumento con respecto a las tarifas antiguas. |
| Recuerda redondear la división a la milésima más cercana para redondear el porcentaje a la décima más cercana. | |
Encuentra el cambio porcentual. (Redondear a la décima más cercana de un porcentaje.) En 2011, el IRS incrementó el costo de kilometraje deducible a 55.5 centavos de 51 centavos.
- Contestar
-
\(8.8 \% \)
Encuentra el cambio porcentual. (Redondear a la décima más cercana de un porcentaje.) En 1995, la tarifa estándar de autobús en Chicago era de 1,50 dólares. En 2008, la tarifa estándar del autobús era de 2.25.
- Contestar
-
\(50%\)
Las aplicaciones de descuento y margen de beneficio son muy comunes en entornos minoristas.
Cuando compras un artículo a la venta, el precio original ha sido descontado por alguna cantidad en dólares. La tasa de descuento, generalmente dada como porcentaje, se utiliza para determinar el monto del descuento. Para determinar el monto del descuento, multiplicamos la tasa de descuento por el precio original.
El precio que paga un minorista por un artículo se llama costo original. El minorista luego agrega un margen al costo original para obtener el precio de lista, el precio por el que vende el artículo. El margen suele calcularse como un porcentaje del costo original. Para determinar la cantidad de margen, multiplique la tasa de recargo por el costo original.
\[ \begin{align*} \text{amount of discount} &= \text{discount rate}· \text{original price} \\ \text{sale price} &= \text{original amount}– \text{discount price} \end{align*}\]
El precio de venta siempre debe ser menor que el precio original.
\[\begin{align*} \text{amount of mark-up} &= \text{mark-up rate}·\text{original price} \\ \text{list price} &= \text{original cost}–\text{mark-up} \end{align*}\]
El precio de lista siempre debe ser superior al costo original.
La galería de arte de Liam compró una pintura a un costo original de 750 dólares. Liam marcó el precio arriba 40%. Encuentra
- la cantidad de margen de beneficio y
- el precio de lista de la pintura.
Solución:
a.
| Identifica lo que te piden encontrar, y elige una variable para representarlo. | ¿Cuál es la cantidad de margen de beneficio? Dejar que\(m=\) la cantidad de margen de beneficio. |
| Escribe una frase que dé la información para encontrarla. | 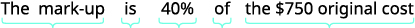 |
| Traducir en una ecuación. |  |
| Resuelve la ecuación. |  |
| Escribe una oración completa. | El margen de beneficio en la pintura fue de 300 dólares. |
| Identifica lo que te piden encontrar, y elige una variable para representarlo. | ¿Cuál es el precio de lista? Deja\(p=\) el precio de lista. |
| Escribe una frase que dé la información para encontrarla. |  |
| Traducir en una ecuación. | 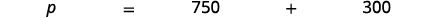 |
| Resuelve la ecuación. |  |
| Cheque. | ¿El precio de lista es mayor que el costo original? ¿$1,050 es más de $750? Sí. |
| Escribe una oración completa. | El precio de lista de la pintura fue de $1,050. |
Encuentra a. la cantidad de mark-up y b. el precio de lista: Jim's music store compró una guitarra a costo original $1,200. Jim marcó el precio arriba 50%.
- Contestar
-
a. $600 b. $1,800
Encuentra a. la cantidad de margen y b. el precio de lista: The Auto Reventa Store compró Pablo's Toyota por $8,500. Marcaron el precio al alza 35%.
- Contestar
-
a. $2,975 b. $11,475
Resolver aplicaciones de interés simple
El interés es parte de nuestra vida cotidiana. Desde los intereses ganados por nuestros ahorros hasta los intereses que pagamos por un préstamo de automóvil o deuda de tarjeta de crédito, todos tenemos alguna experiencia con el interés en nuestras vidas.
La cantidad de dinero que depositas inicialmente en un banco se llama el principal,\(P,\) y el banco te paga intereses,\(I.\) Cuando tomas un préstamo, pagas intereses sobre la cantidad que pides prestado, también llamado el principal.
En cualquier caso, el interés se calcula como un cierto porcentaje del principal, denominado la tasa de interés,\(r.\) La tasa de interés suele expresarse como un porcentaje anual, y se calcula utilizando el equivalente decimal del porcentaje. La variable\(t,\) (por tiempo) representa el número de años en que se ahorra o se toma prestado el dinero.
El interés se calcula como interés simple o interés compuesto. Aquí usaremos interés simple.
Si una cantidad de dinero,\(P,\) llamada principal, se invierte o toma prestada por un periodo de\(t\) años a una tasa de interés anual\(r,\) la cantidad de intereses,\(I,\) devengados o pagados es
\[ \begin{array}{ll} I=Prt \; \; \; \; \; \; \; \; \; \; \; \; \text{where} & { \begin{align*} I &= \text{interest} \\ P &= \text{principal} \\ r &= \text{rate} \\ t &= \text{time} \end{align*}} \end{array}\]
Los intereses devengados o pagados de acuerdo con esta fórmula se denominan intereses simples.
La fórmula que utilizamos para calcular el interés es\(I=Prt\). Para usar la fórmula sustituimos en los valores las variables que se dan, y luego resolvemos por la variable desconocida. Puede ser útil organizar la información en un gráfico.
Areli invirtió un principal de 950 dólares en su cuenta bancaria que obtuvo intereses simples a una tasa de interés del 3%. ¿Cuánto interés ganó en cinco años?
Solución:
\( \begin{aligned} I & = \; ? \\ P & = \; \$ 950 \\ r & = \; 3 \% \\ t & = \; 5 \text{ years} \end{aligned}\)
\(\begin{array}{ll} \text{Identify what you are asked to find, and choose a} & \text{What is the simple interest?} \\ \text{variable to represent it.} & \text{Let } I= \text{interest.} \\ \text{Write the formula.} & I=Prt \\ \text{Substitute in the given information.} & I=(950)(0.03)(5) \\ \text{Simplify.} & I=142.5 \\ \text{Check.} \\ \text{Is } \$142.50 \text{ a reasonable amount of interest on } \$ \text{ 950?} \; \;\;\;\;\; \;\;\;\;\;\; \\ \text{Yes.} \\ \text{Write a complete sentence.} & \text{The interest is } \$ \text{142.50.} \end{array}\)
Nathaly depositó $12,500 en su cuenta bancaria donde ganará 4% de interés simple. ¿Cuánto interés ganará Nathaly en cinco años?
- Contestar
-
Ganará $2,500.
Susana invirtió un principal de 36,000 dólares en su cuenta bancaria que obtuvo intereses simples a una tasa de interés de 6.5%. ¿Cuánto interés ganó en tres años?
- Contestar
-
Ella ganó $7,020.
Puede haber ocasiones en las que sepamos la cantidad de intereses ganados sobre un principal determinado durante un cierto período de tiempo, pero desconocemos la tasa.
Colgar prestado $7,500 de sus padres para pagar su colegiatura. En cinco años, les pagó 1.500 dólares de interés además de los $7,500 que pidió prestados. ¿Cuál era la tasa de interés simple?
Solución:
\( \begin{aligned} I & = \; \$ 1500 \\ P & = \; \$ 7500 \\ r & = \; ? \\ t & = \; 5 \text{ years} \end{aligned}\)
\ (\ text {Identifica lo que te piden encontrar,}\ qquad\ quad\ text {¿Qué es la tasa de interés simple?} \\
\ begin {align*}
&\ text {y elija una variable para representarlo.} &\ text {Dejar} r\; &=\;\ text {tasa de interés}\\
&\ text {Escribe la fórmula.} & I\; &=\; Prt\\
&\ text {Sustituir en la información dada.} & 1,500\; &=\; (7.500) r (5)\\
&\ text {Multiplicar.} & 1,500\; &=\; 37,500r\\
&\ text {Dividir.} & 0.04\; &=\; r\\
&\ text {Cambiar a forma porcentual} & r\; &=\; 4\%
\ end {align*}\)
Cheque.
\ (\ begin {align*} I\; &=\; Prt\\
1,500\; &\ stackrel {?} {=}\; (7.500) (0.04) (5)\\
1,500\; &=\; 1,500 ✓\ final {alinear*}\)
Escribe una oración completa. La tasa de interés fue\(4\%.\)
Jim le prestó a su hermana 5.000 dólares para ayudarla a comprar una casa. En tres años, ella le pagó los 5.000 dólares, más 900 dólares de interés. ¿Cuál era la tasa de interés simple?
- Contestar
-
La tasa de interés simple fue de 6%.
Loren prestó a su hermano 3.000 dólares para que le ayudara a comprar un auto. En cuatro años, su hermano le devolvió los 3.000 dólares más 660 dólares en intereses. ¿Cuál era la tasa de interés simple?
- Contestar
-
La tasa de interés simple fue de 5.5%.
En el siguiente ejemplo, se nos pide encontrar el principal, la cantidad prestada.
El estado de cuenta de préstamo para auto nuevo de Sean dijo que pagaría $4,866.25 en interés de una tasa de interés simple de 8.5% en cinco años. ¿Cuánto pidió prestado para comprar su auto nuevo?
Solución:
\( \begin{aligned} I & = \; 4,866.25 \\ P & = \; ? \\ r & = \; 8.5 \% \\ t & = \; 5 \text{ years} \end{aligned}\)
\ (\ text {Identifica lo que te piden encontrar,}\ qquad\ quad\ text {¿Cuál es la cantidad prestada (el principal)?} \\
\ begin {align*}
&\ text {y elija una variable para representarlo.} &\ text {Dejar} P\; &=\;\ text {principal prestado}\\
&\ text {Escribe la fórmula.} & I\; &=\; Prt\\
&\ text {Sustituir en la información dada.} & 4,866.25\; &=\; P (0.085) (5)\\
&\ text {Multiplicar.} & 4,866.25\; &=\; 0.425P\\
&\ text {Dividir.} & 11.450\; &=\; P
\ final {alinear*}\)
Cheque.
\ (\ begin {align*} I\; &=\; Prt\\
4,866.25\; &\ stackrel {?} {=}\; (11,450) (0.085) (5)\\
4.866.25\; &=\; 4,866.25 ✓\ end {align*}\)
Escribe una oración completa. El director fue\($11,450.\)
Eduardo se percató de que sus nuevos papeles de préstamo de auto establecían que con una tasa de interés simple de 7.5%, pagaría $6,596.25 en intereses a lo largo de cinco años. ¿Cuánto pidió prestado para pagar su auto?
- Contestar
-
Pagó $17,590.
En cinco años, la cuenta bancaria de Gloria obtuvo 2.400 dólares de interés al 5% de interés simple. ¿Cuánto había depositado en la cuenta?
- Contestar
-
Ella depositó 9.600 dólares.
Acceda a este recurso en línea para obtener instrucción adicional y práctica con el uso de una estrategia de resolución de problemas.
- Problemas aritméticos iniciales
Conceptos clave
- Cómo usar una estrategia de resolución de problemas para problemas de palabras
- Lee el problema. Asegúrate de que todas las palabras e ideas sean entendidas.
- Identifica lo que buscas.
- Nombra lo que buscas. Elija una variable para representar esa cantidad.
- Traducir en una ecuación. Puede ser útil reafirmar el problema en una oración con toda la información importante. Después, traducir la oración en inglés a una ecuación álgebra.
- Resolver la ecuación utilizando técnicas de álgebra adecuadas.
- Verifique la respuesta en el problema para asegurarse de que tenga sentido.
- Contesta la pregunta con una oración completa.
- Cómo encontrar el cambio porcentual
- Encuentra la cantidad de cambio
\(\text{change}=\text{new amount}−\text{original amount}\)
- Encuentra qué porcentaje es la cantidad de cambio de la cantidad original.
\(\text{change is what percent of the original amount?}\)
- Encuentra la cantidad de cambio
- \( \begin{align*} \text{amount of discount} &= \text{discount rate}· \text{original price} \\ \text{sale price} &= \text{original amount}– \text{discount price} \end{align*}\)
- \(\begin{align*} \text{amount of mark-up} &= \text{mark-up rate}·\text{original price} \\ \text{list price} &= \text{original cost}–\text{mark-up} \end{align*}\)
- Si una cantidad de dinero,\(P,\) llamada principal, se invierte o toma prestada por un periodo de t años a una tasa de interés anual\(r,\) la cantidad de intereses,\(I,\) devengados o pagados es:\[\begin{aligned} &{} &{} &{I=interest} \nonumber\\ &{I=Prt} &{\text{where} \space} &{P=principal} \nonumber\\ &{} &{\space} &{r=rate} \nonumber\\ &{} &{\space} &{t=time} \nonumber \end{aligned}\]