3.2: Gráfica ecuaciones lineales en dos variables
- Page ID
- 112291
Al final de esta sección, podrás:
- Trazar puntos en un sistema de coordenadas rectangulares
- Graficar una ecuación lineal trazando puntos
- Graficar líneas verticales y horizontales
- Encuentra los\(x\) - y\(y\) -interceptos
- Graficar una línea usando las intercepciones
Trazar puntos en un sistema de coordenadas rectangulares
Al igual que los mapas utilizan un sistema de cuadrícula para identificar ubicaciones, un sistema de cuadrícula se usa en álgebra para mostrar una relación entre dos variables en un sistema de coordenadas rectangular. El sistema de coordenadas rectangulares también se denomina\(xy\) plano -plano o “plano de coordenadas”.
El sistema de coordenadas rectangulares está formado por dos líneas numéricas que se cruzan, una horizontal y otra vertical. La línea numérica horizontal se llama el\(x\) eje -axis. La línea numérica vertical se llama el\(y\) eje -axis. Estos ejes dividen un plano en cuatro regiones, llamadas cuadrantes. Los cuadrantes se identifican por números romanos, comenzando en la parte superior derecha y avanzando en sentido antihorario. Ver Figura\(\PageIndex{1}\).
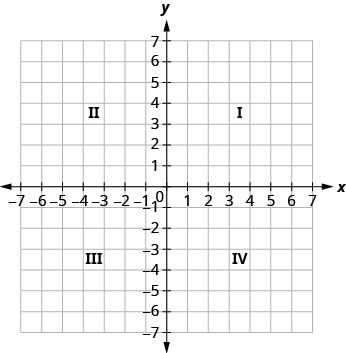
En el sistema de coordenadas rectangulares, cada punto está representado por un par ordenado. El primer número del par ordenado es la\(x\) coordenada del punto, y el segundo número es la\(y\) coordenada del punto. La frase “par ordenado” significa que el orden es importante.
Un par ordenado,\((x,y)\) da las coordenadas de un punto en un sistema de coordenadas rectangular. El primer número es la\(x\) coordenada. El segundo número es la\(y\) coordenada.
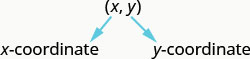
¿Cuál es el par ordenado del punto donde se cruzan los ejes? En ese punto ambas coordenadas son cero, por lo que su par ordenado es\((0,0)\) .El punto\((0,0)\) tiene un nombre especial. Se llama el origen.
Al punto\((0,0)\) se le llama el origen. Es el punto donde se cruzan los\(x\) ejes\(y\) -axis y -axis.
Utilizamos las coordenadas para localizar un punto en el\(xy\) plano. Trazar el punto\((1,3)\) como ejemplo. Primero, ubique 1 en el\(x\) eje y dibuje ligeramente una línea vertical a través\(x=1\). Luego, localice\(3\) en el\(y\) eje -y dibuje una línea horizontal a través de\(y=3.\) Ahora, encuentre el punto donde se encuentran estas dos líneas, es decir, el punto con coordenadas\((1,3)\). Ver Figura\(\PageIndex{2}\).
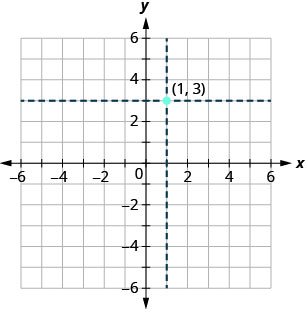
Observe que la línea vertical a través\(x=1\) y la línea horizontal a través no\(y=3\) forman parte de la gráfica. Simplemente los usamos para ayudarnos a localizar el punto\((1,3)\).
Cuando una de las coordenadas es cero, el punto se encuentra en uno de los ejes. En\(\PageIndex{3},\) la Figura el punto\((0,4)\) está en el\(y\) eje -y el punto\((−2,0)\) está en el\(x\) eje -eje.
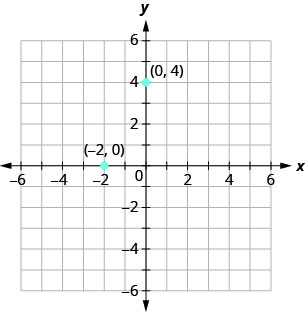
- Los puntos con una\(y\) coordenada -igual a\(0\) están en el\(x\) eje -y tienen coordenadas\((a,0)\).
- Los puntos con una\(x\) coordenada -igual a\(0\) están en el\(y\) eje -y tienen coordenadas\((0,b)\).
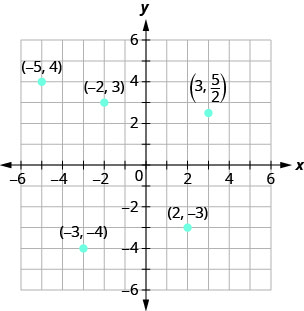
Trazar cada punto en el sistema de coordenadas rectangulares e identificar el cuadrante en el que se encuentra el punto:
a.\((−5,4\)) b.\((−3,−4)\) c.\((2,−3)\) d.\((0,−1)\) e\((3,\dfrac{5}{2})\).
Solución
El primer número del par de coordenadas es la\(x\) coordenada -y el segundo número es la\(y\) coordenada. Para trazar cada punto, esboce una línea vertical a través de la\(x\) coordenada y una línea horizontal a través de la\(y\) coordenada. Su intersección es el punto.
- Ya que\(x=−5\), el punto está a la izquierda del\(y\) eje -. También, ya que\(y=4\), el punto está por encima del\(x\) eje -eje. El punto\((−5,4)\) está en el Cuadrante II.
- Ya que\(x=−3\), el punto está a la izquierda del\(y\) eje -. También, ya que\(y=−4\), el punto se encuentra por debajo del\(x\) eje -eje. El punto\((−3,−4)\) está en el Cuadrante III.
- Ya que\(x=2\), el punto está a la derecha del\(y\) eje -. Ya que\(y=−3\), el punto está por debajo del\(x\) eje -. El punto\((2,−3)\) está en el Cuadrante IV.
- Ya que\(x=0\), el punto cuyas coordenadas están\((0,−1)\) está en el\(y\) eje -eje.
- Ya que\(x=3\), el punto está a la derecha del\(y\) eje -. Ya que\(y=\dfrac{5}{2})\), el punto está por encima del\(x\) eje -. (Puede ser útil escribir\(\dfrac{5}{2})\) como un número mixto o decimal). El punto\((3,\dfrac{5}{2})\) está en el Cuadrante I.
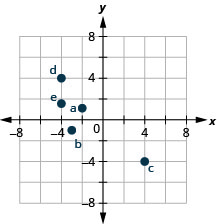
Trazar cada punto en un sistema de coordenadas rectangulares e identificar el cuadrante en el que se encuentra el punto:
a.\((−2,1)\) b.\((−3,−1)\) c.\((4,−4)\) d.\((−4,4)\) e.\((−4,\dfrac{3}{2})\)
- Contestar
-
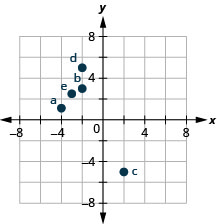
Trazar cada punto en un sistema de coordenadas rectangulares e identificar el cuadrante en el que se encuentra el punto:
a.\((−4,1)\) b.\((−2,3)\) c.\((2,−5)\) d.\((−2,5)\) e.\((−3,\dfrac{5}{2})\)
- Contestar
-
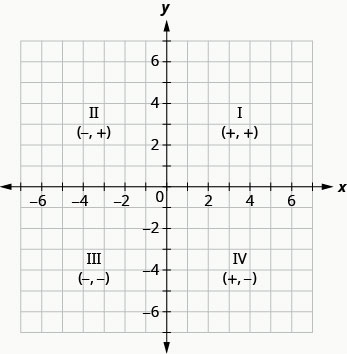
Los signos de la\(x\) coordenada y la\(y\) coordenada afectan la ubicación de los puntos. Es posible que hayas notado algunos patrones a medida que graficaste los puntos en el ejemplo anterior. Podemos resumir los patrones de signos de los cuadrantes de esta manera:
| Cuadrante I | Cuadrante II | Cuadrante III | Cuadrante IV |
| \((x,y)\) | \((x,y)\) | \((x,y)\) | \((x,y)\) |
| \((+,+)\) | \((−,+)\) | \((−,−)\) | \((+,−)\) |
Hasta ahora, todas las ecuaciones que has resuelto eran ecuaciones con una sola variable. En casi todos los casos, cuando resolviste la ecuación obtuviste exactamente una solución. Pero las ecuaciones pueden tener más de una variable. Las ecuaciones con dos variables pueden ser de la forma\(Ax+By=C\). Una ecuación de esta forma se denomina ecuación lineal en dos variables.
Una ecuación de la forma\(Ax+By=C\), donde\(A\) y no\(B\) son ambos cero, se denomina ecuación lineal en dos variables.
Aquí hay un ejemplo de una ecuación lineal en dos variables,\(x\) y\(y\).
\ (\ begin {align*} {\ color {BrickRed} A} x + {\ color {RoyalBlue} B} y &= {\ color {forestgreen} C}\\ [5pt]
x+ {\ color {RoyalBlue} 4} y &= {\ color {forestgreen} 8}\ end {align*}\)
\({\color{BrickRed}A = 1}\),\({\color{RoyalBlue}B = 4}\),\({\color{forestgreen}C=8}\)
La ecuación\(y=−3x+5\) es también una ecuación lineal. Pero no parece estar en la forma\(Ax+By=C\). Podemos usar la Propiedad de Adición de Igualdad y reescribirla en\(Ax+By=C\) forma.
\[ \begin{array} {lrll} {} &{y} &= &{-3x+5} \\ {\text{Add to both sides.} } &{y+3x} &= &{3x+5+3x} \\ {\text{Simplify.} } &{y+3x} &= &{5} \\ {\text{Use the Commutative Property to put it in} } &{} &{} &{} \\ {Ax+By=C\text{ form.} } &{3x+y} &= &{5} \end{array} \nonumber\]
Al reescribir\(y=−3x+5\) como\(3x+y=5\), podemos ver fácilmente que se trata de una ecuación lineal en dos variables porque es de la forma\(Ax+By=C\). Cuando una ecuación está en la forma\(Ax+By=C\), decimos que está en forma estándar de una ecuación lineal.
Una ecuación lineal está en forma estándar cuando se escribe\(Ax+By=C\).
La mayoría de la gente prefiere tener\(A,\)\(B,\) y\(C\) ser enteros y\(A \geq 0\) al escribir una ecuación lineal en forma estándar, aunque no es estrictamente necesaria.
Las ecuaciones lineales tienen infinitamente muchas soluciones. Por cada número que se sustituye\(x\) hay un\(y\) valor -correspondiente. Este par de valores es una solución a la ecuación lineal y está representado por el par ordenado\((x,y)\). Cuando sustituimos estos valores de\(x\) y\(y\) en la ecuación, el resultado es una declaración verdadera, porque el valor del lado izquierdo es igual al valor del lado derecho.
Un par ordenado\((x,y)\) es una solución de la ecuación lineal\(Ax+By=C\), si la ecuación es una declaración verdadera cuando los\(y\) valores\(x\) - y -del par ordenado se sustituyen en la ecuación.
Las ecuaciones lineales tienen infinitamente muchas soluciones. Podemos trazar estas soluciones en el sistema de coordenadas rectangulares. Los puntos se alinearán perfectamente en línea recta. Conectamos los puntos con una línea recta para obtener la gráfica de la ecuación. Ponemos flechas en los extremos de cada lado de la línea para indicar que la línea continúa en ambos sentidos.
Una gráfica es una representación visual de todas las soluciones de la ecuación. Es un ejemplo del dicho: “Una imagen vale más que mil palabras”. La línea te muestra todas las soluciones a esa ecuación. Cada punto de la línea es una solución de la ecuación. Y, cada solución de esta ecuación está en esta línea. Esta línea se llama la gráfica de la ecuación. ¡Los puntos que no están en la línea no son soluciones!
La gráfica de una ecuación lineal\(Ax+By=C\) es una línea recta.
- Cada punto de la línea es una solución de la ecuación.
- Toda solución de esta ecuación es un punto en esta línea.
Se muestra la\(y=2x−3\) gráfica de.
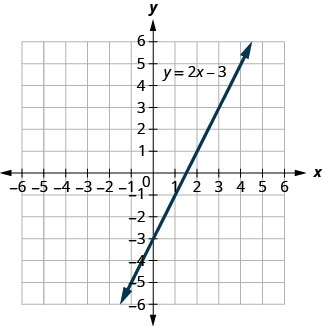
Por cada par ordenado, decida:
- ¿El par ordenado es una solución a la ecuación?
- ¿Está el punto en la línea?
A:\((0,−3)\) B:\((3,3)\) C:\((2,−3)\) D:\((−1,−5)\)
Solución:
Sustituya los\(y\) valores\(x\) - y -en la ecuación para verificar si el par ordenado es una solución a la ecuación.
a.
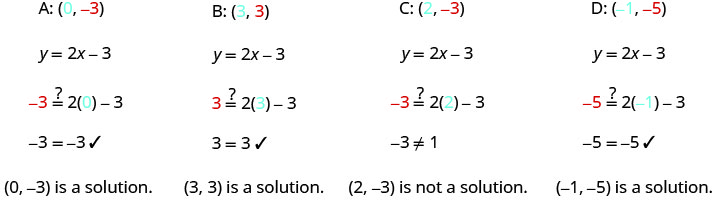
b. trazar los puntos\((0,−3)\),\((3,3)\),\((2,−3)\), y\((−1,−5)\).
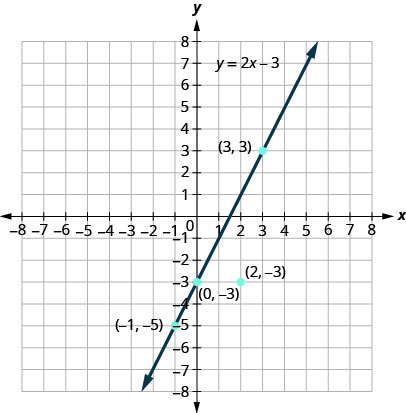
Los puntos\((0,3)\),\((3,−3)\), y\((−1,−5)\) están en la línea\(y=2x−3\), y el punto no\((2,−3)\) está en la línea.
Los puntos a los que son soluciones\(y=2x−3\) están en la línea, pero el punto que no es una solución no está en la línea.
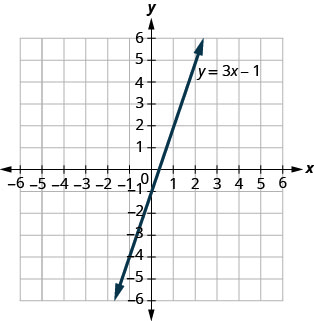
Usar gráfica de\(y=3x−1\). Por cada par ordenado, decida:
a. ¿El par ordenado es una solución a la ecuación?
b. ¿El punto está en la línea?
A\((0,−1)\) B\((2,5)\)
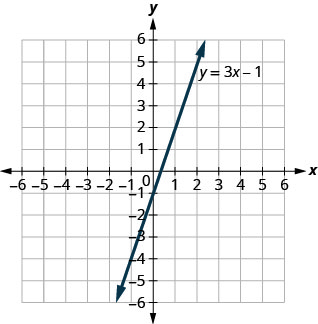
- Contestar
-
a. si b. si
Usar gráfica de\(y=3x−1\). Por cada par ordenado, decida:
a. ¿El par ordenado es una solución a la ecuación?
b. ¿El punto está en la línea?
A\((3,−1)\) B\((−1,−4)\)
- Contestar
-
a. no b. si
Graficar una ecuación lineal trazando puntos
Existen varios métodos que se pueden utilizar para graficar una ecuación lineal. El primer método que usaremos se llama puntos de trazado, o Método de trazado de puntos. Encontramos tres puntos cuyas coordenadas son soluciones a la ecuación y luego los trazamos en un sistema de coordenadas rectangular. Al conectar estos puntos en una línea, tenemos la gráfica de la ecuación lineal.
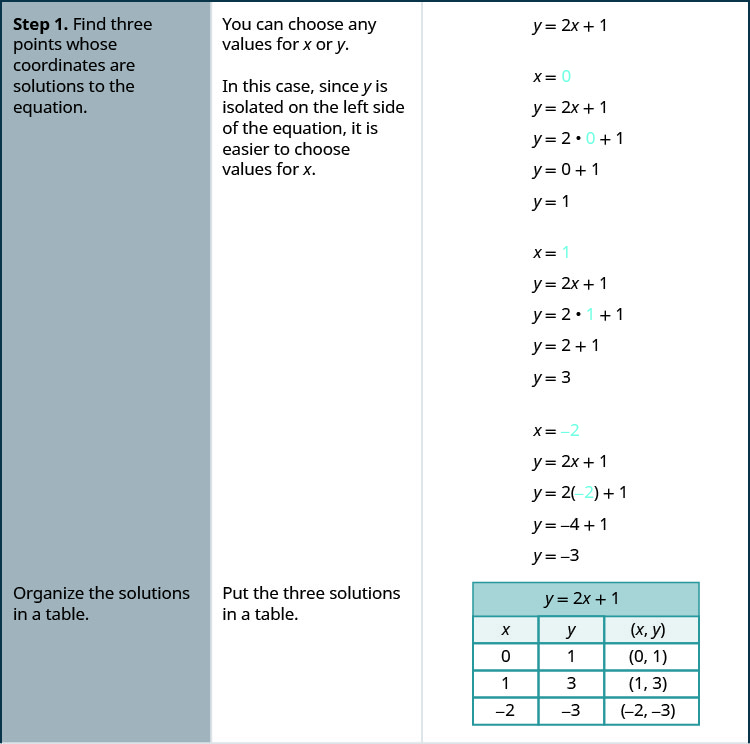
Grafica la ecuación\(y=2x+1\) trazando puntos.
Solución:
Grafica la ecuación trazando puntos:\(y=2x−3\).
- Contestar
-
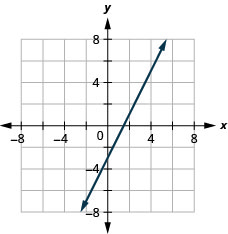
Grafica la ecuación trazando puntos:\(y=−2x+4\).
- Contestar
-
Aquí se resumen los pasos a seguir al graficar una ecuación lineal trazando puntos.
- Encuentra tres puntos cuyas coordenadas son soluciones a la ecuación. Organizarlos en una mesa.
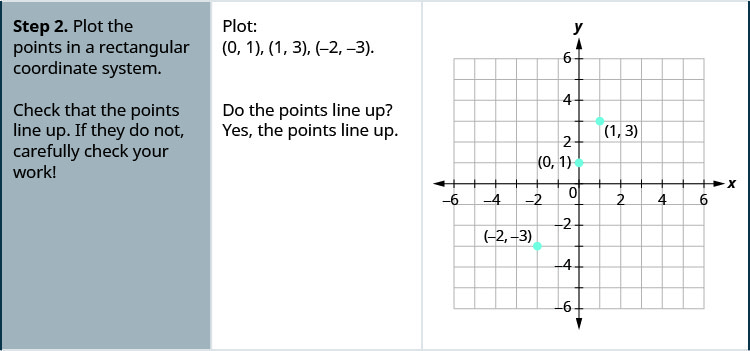
- Trazar los puntos en un sistema de coordenadas rectangulares. Comprueba que los puntos se alineen. Si no lo hacen, revisa cuidadosamente tu trabajo.
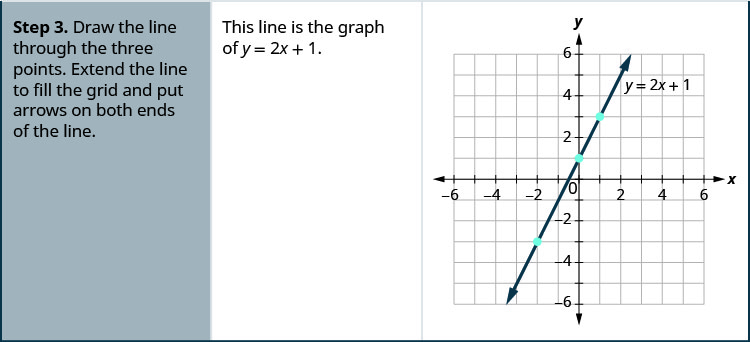
- Dibuja la línea a través de los tres puntos. Extiende la línea para llenar la cuadrícula y coloca flechas en ambos extremos de la línea.
Es cierto que sólo se necesitan dos puntos para determinar una línea, pero es un buen hábito usar tres puntos. Si solo trazas dos puntos y uno de ellos es incorrecto, aún puedes dibujar una línea pero no representará las soluciones a la ecuación. Será la línea equivocada.
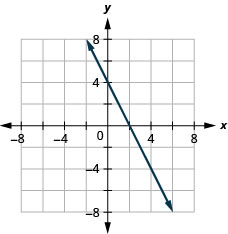
Si usas tres puntos, y uno es incorrecto, los puntos no se alinearán. Esto te dice que algo anda mal y necesitas revisar tu trabajo. Mira la diferencia entre estas ilustraciones.

Cuando una ecuación incluye una fracción como coeficiente de todavía\(x,\) podemos sustituir cualquier número por\(x.\) Pero la aritmética es más fácil si hacemos “buenas” elecciones para los valores de De\(x.\) esta manera evitaremos respuestas fraccionarias, que son difíciles de graficar con precisión.
Grafica la ecuación:\(y=\frac{1}{2}x+3\).
Solución:
Encuentra tres puntos que son soluciones a la ecuación. Dado que esta ecuación tiene la fracción\(\dfrac{1}{2}\) como coeficiente de\(x,\) elegiremos valores de\(x\) cuidadosamente. Usaremos cero como una opción y múltiplos de\(2\) para las otras opciones. ¿Por qué los múltiplos de dos son una buena opción para los valores de\(x\)? Al elegir múltiplos de\(2\) la multiplicación por\(\dfrac{1}{2}\) simplifica a un número entero
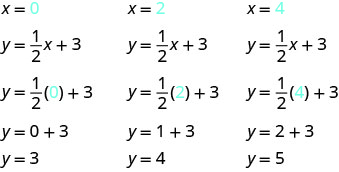
Los puntos se muestran en la Tabla.
| \(y=\frac{1}{2}x+3\) | ||
| \(x\) | \(y\) | \((x,y)\) |
| 0 | 3 | \((0,3)\) |
| 2 | 4 | \((2,4)\) |
| 4 | 5 | \((4,5)\) |
Trace los puntos, verifique que se alineen y dibuje la línea.
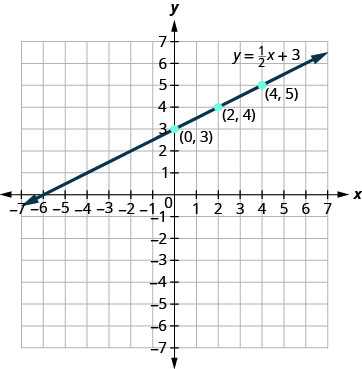
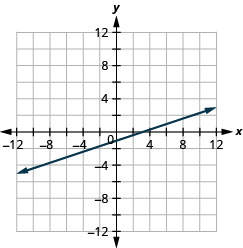
Grafica la ecuación:\(y=\frac{1}{3}x−1\).
- Contestar
-
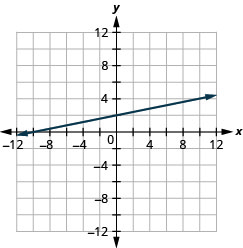
Grafica la ecuación:\(y=\frac{1}{4}x+2\).
- Contestar
-
Gráfica Líneas Verticales y Horizontales
Algunas ecuaciones lineales tienen sólo una variable. Pueden tener justo\(x\) y no\(y,\) o simplemente\(y\) sin un\(x.\) Esto cambia la forma en que hacemos una tabla de valores para obtener los puntos para trazar.
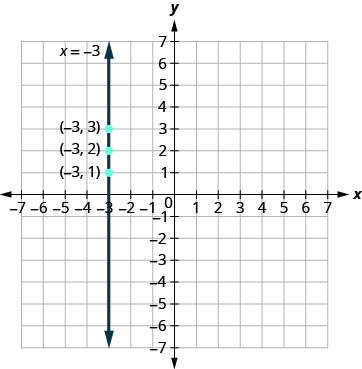
Consideremos la ecuación\(x=−3\). Esta ecuación tiene sólo una variable,\(x.\) La ecuación dice que siempre\(x\) es igual a\(−3\), por lo que su valor no depende de\(y.\) No importa cuál sea el valor\(y,\) del valor de\(x\) es siempre\(−3\).
Entonces, para hacer una tabla de valores, escriba\(−3\) para todos los\(x\) -valores. Entonces elige cualquier valor para\(y.\) Ya que\(x\) no depende de\(y,\) puedes elegir cualquier número que te guste. Pero para ajustar los puntos en nuestra gráfica de coordenadas, usaremos 1, 2 y 3 para las\(y\) coordenadas. Ver Tabla.
| \(x=−3\) | ||
| \(x\) | \(y\) | \((x,y)\) |
| \(−3\) | 1 | \((−3,1)\) |
| \(−3\) | 2 | \((−3,2)\) |
| \((−3,)\) | 3 | \((−3,3)\) |
Trace los puntos de la mesa y conéctelos con una línea recta. Observe que hemos graficado una línea vertical.
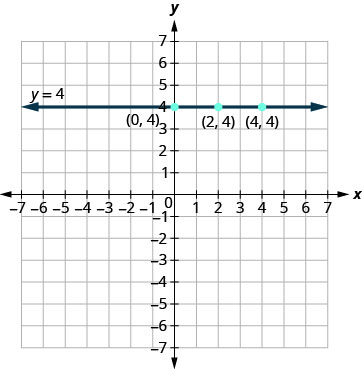
¿Y si la ecuación tiene\(y\) pero no\(x\)? Vamos a graficar la ecuación\(y=4\). Esta vez el valor y- es una constante, por lo que en esta ecuación,\(y\) no depende de\(x.\) Rellenar\(4\) para todos los\(y\)'s en Tabla y luego elegir cualquier valor para\(x.\) Vamos a usar 0, 2, y 4 para las\(x\) coordenadas -.
| \(y=4\) | ||
| \(x\) | \(y\) | \((x,y)\) |
| 0 | 4 | \((0,4)\) |
| 2 | 4 | \((2,4)\) |
| 4 | 4 | \((4,4)\) |
En esta figura, hemos graficado una línea horizontal que pasa por el\(y\) eje -en\(4.\)
Una línea vertical es la gráfica de una ecuación de la forma\(x=a\).
La línea pasa a través del\(x\) eje -en\((a,0)\).
Una línea horizontal es la gráfica de una ecuación de la forma\(y=b\).
La línea pasa a través del\(y\) eje -en\((0,b)\).
Gráfica: a.\(x=2\) b\(y=−1\).
Solución
a. la ecuación tiene solo una variable,\(x,\) y siempre\(x\) es igual a\(2.\) Creamos una tabla donde\(x\) está siempre\(2\) y luego ponemos cualquier valor para\(y.\) La gráfica es una línea vertical que pasa por el\(x\) eje -en\(2.\)
| \(x\) | \(y\) | \((x,y)\) |
|---|---|---|
| \ (x\)” datos-valign="middle">2 | \ (y\)” datos-valign="middle">1 | \ ((x, y)\)” datos-valign="middle">\((2,1)\) |
| \ (x\)” datos-valign="middle">2 | \ (y\)” datos-valign="middle">2 | \ ((x, y)\)” datos-valign="middle">\((2,2)\) |
| \ (x\)” datos-valign="middle">2 | \ (y\)” datos-valign="middle">3 | \ ((x, y)\)” datos-valign="middle">\((2,3)\) |
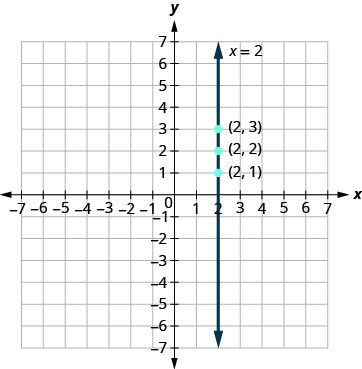
b. del mismo modo, la ecuación\(y=−1\) tiene sólo una variable,\(y\). El valor de\(y\) es constante. Todos los pares ordenados en la siguiente tabla tienen la misma\(y\) coordenada. La gráfica es una línea horizontal que pasa por el\(y\) eje -en\(−1.\)
| \(\mathbf{x}\) | \(\mathbf{ y}\) | \(\mathbf{(x,y)}\) |
|---|---|---|
| \ (\ mathbf {x}\)” datos-valign="middle">0 | \ (\ mathbf {y}\)” datos-valign="middle">\(−1\) | \ (\ mathbf {(x, y)}\)” datos-valign="middle">\((0,−1)\) |
| \ (\ mathbf {x}\)” datos-valign="middle">3 | \ (\ mathbf {y}\)” datos-valign="middle">\(−1\) | \ (\ mathbf {(x, y)}\)” datos-valign="middle">\((3,−1)\) |
| \ (\ mathbf {x}\)” datos-valign="middle">\(−3\) | \ (\ mathbf {y}\)” datos-valign="middle">\(−1\) | \ (\ mathbf {(x, y)}\)” datos-valign="middle">\((−3,−1)\) |
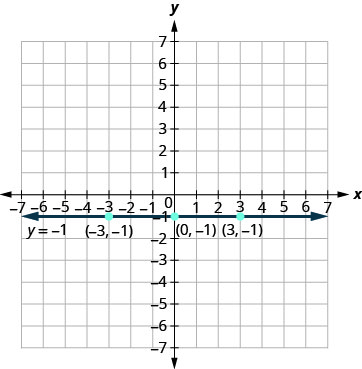
G raph las ecuaciones: a.\(x=5\) b. \(y=−4\).
- Contestar
-
a.
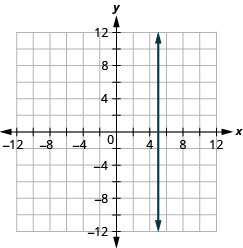
b.
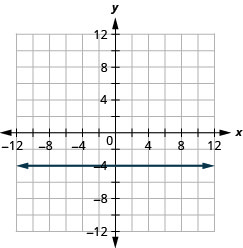
G raph las ecuaciones: a.\(x=−2\) b. \(y=3\).
- Contestar
-
a.
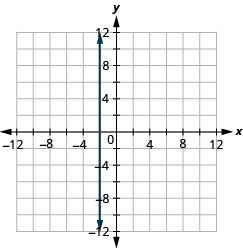
b.
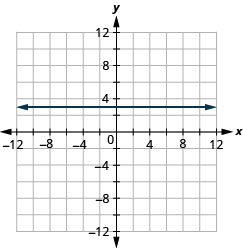
¿Cuál es la diferencia entre las ecuaciones\(y=4x\) y\(y=4\)?
La ecuación\(y=4x\) tiene ambos\(x\) y\(y.\) El valor de\(y\) depende del valor de\(x,\) por lo que la\(y\) coordenada -cambia de acuerdo con el valor de\(x.\) La ecuación\(y=4\) tiene solo una variable. El valor de\(y\) es constante, no depende del valor de\(x,\) por lo que la\(y\) coordenada -siempre es\(4.\)
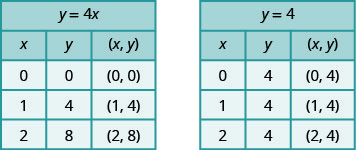
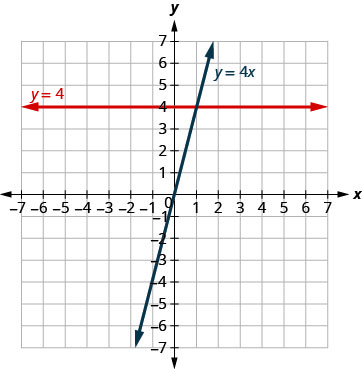
Observe, en la gráfica, la ecuación\(y=4x\) da una línea inclinada, mientras que\(y=4\) da una línea horizontal.
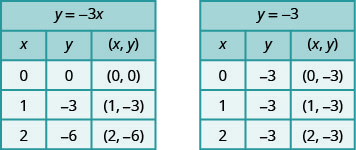
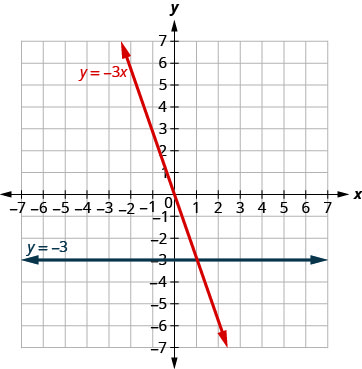
Gráfica\(y=−3x\) y\(y=−3\) en el mismo sistema de coordenadas rectangulares.
Solución:
Notamos que la primera ecuación tiene la variable\(x,\) mientras que la segunda no. Hacemos una tabla de puntos para cada ecuación y luego graficamos las líneas. Se muestran las dos gráficas.
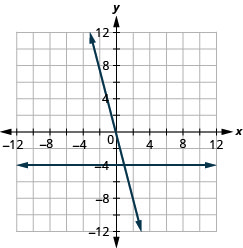
Grafique las ecuaciones en el mismo sistema de coordenadas rectangulares:\(y=−4x\) y\(y=−4\).
- Contestar
-
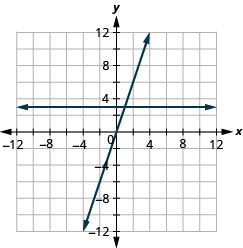
Grafique las ecuaciones en el mismo sistema de coordenadas rectangulares:\(y=3\) y\(y=3x\).
- Contestar
-
Buscar\(x\) - y\(y\) -intercepciones
Cada ecuación lineal puede ser representada por una línea única que muestra todas las soluciones de la ecuación. Hemos visto que al graficar una línea trazando puntos, se puede utilizar cualquiera de tres soluciones para graficar. Esto significa que dos personas que grafican la línea podrían usar diferentes conjuntos de tres puntos.
A primera vista, sus dos líneas podrían no parecer iguales, ya que tendrían diferentes puntos etiquetados. Pero si todo el trabajo se realizó correctamente, las líneas deberían ser exactamente las mismas. Una forma de reconocer que efectivamente son la misma línea es mirar donde la línea cruza el\(x\) eje y el\(y\) eje. A estos puntos se les llama las intercepciones de una línea.
Los puntos donde una línea cruza el\(x\) eje y el\(y\) eje -se denominan las intercepciones de la línea.
Veamos las gráficas de las líneas.
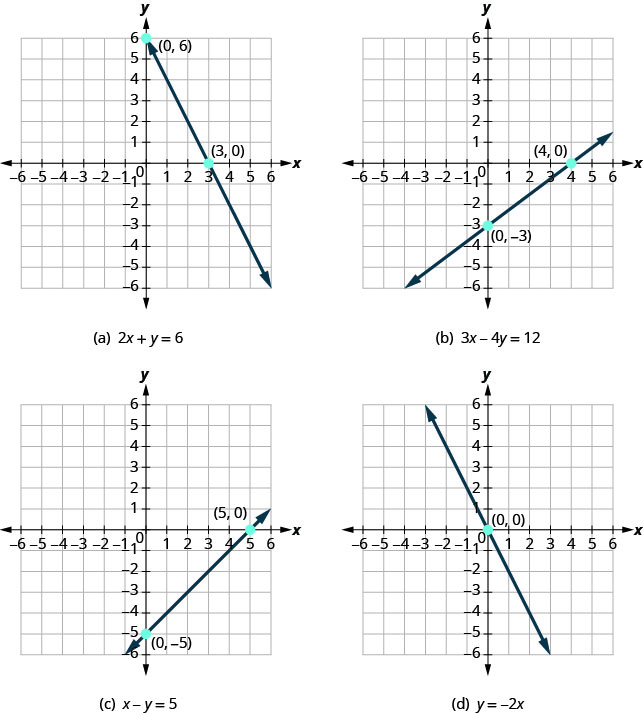
Primero, observe dónde cada una de estas líneas cruza el\(x\) eje -eje. Ver Tabla.
Ahora, veamos los puntos donde estas líneas cruzan el\(y\) eje -eje.
| Figura | La línea cruza el\(x\) eje en: |
Par ordenado para este punto |
La línea cruza el eje y en: |
Par ordenado para este punto |
|---|---|---|---|---|
| Figura (a) | \ (x\) -eje en:” data-valign="middle">\(3\) | \((3,0)\) | \(6\) | \((0,6)\) |
| Figura (b) | \ (x\) -eje en:” data-valign="middle">\(4\) | \((4,0)\) | \(−3\) | \((0,−3)\) |
| Figura (c) | \ (x\) -eje en:” data-valign="middle">\(5\) | \((5,0)\) | \(−5\) | \((0,5)\) |
| Figura (d) | \ (x\) -eje en:” data-valign="middle">\(0\) | \((0,0)\) | \(0\) | \((0,0)\) |
| Figura General | \ (x\) -eje en:” data-valign="middle">\(a\) | \((a,0)\) | \(b\) | \((0,b)\) |
¿Ves un patrón?
Para cada línea, la\(y\) coordenada -del punto donde la línea cruza el\(x\) eje -es cero. El punto donde la línea cruza el\(x\) eje -tiene la forma\((a,0)\) y se llama la\(x\) -intercepción de la línea. La\(x\) -intercepción ocurre cuando\(y\) es cero.
En cada línea, la coordenada\(x\) - del punto donde la línea cruza el\(y\) eje es cero. El punto donde la línea cruza el\(y\) eje -tiene la forma\((0,b)\) y se llama la\(y\) -intercepción de la línea. La\(y\) -intercepción ocurre cuando\(x\) es cero.
La\(x\) intersección es el punto\((a,0)\) donde la línea cruza el\(x\) eje.
La\(y\) intersección es el punto\((0,b)\) donde la línea cruza el\(y\) eje.

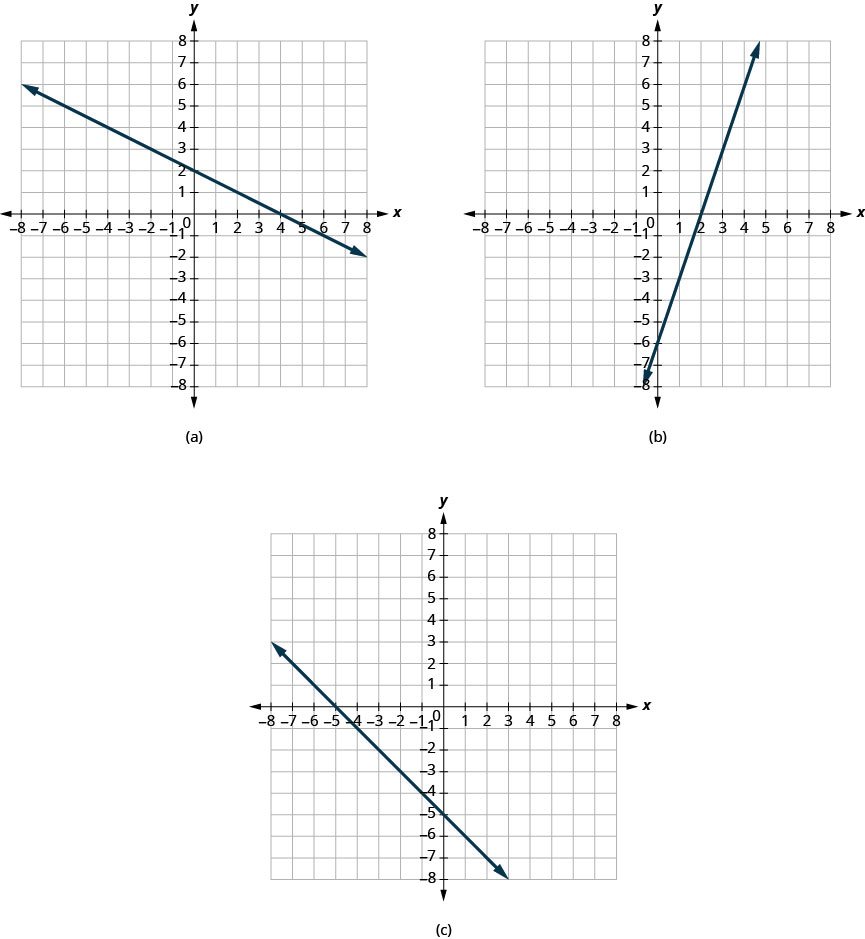
Encuentra las\(y\) intercepciones\(x\) - y -en cada gráfica mostrada.
Solución:
a. La gráfica cruza el\(x\) eje -en el punto\((4,0)\). La x- intercepción es\((4,0)\).
La gráfica cruza el\(y\) eje -en el punto\((0,2)\). El\(y\) -intercepto es\((0,2)\).
b. La gráfica cruza el\(x\) eje -en el punto\((2,0)\). El\(x\) -intercepto es\((2,0)\).
La gráfica cruza el\(y\) eje -en el punto\((0,−6)\). El\(y\) -intercepto es\((0,−6)\).
c. La gráfica cruza el\(x\) eje -en el punto\((−5,0)\). El\(x\) -intercepto es\((−5,0)\).
La gráfica cruza el\(y\) eje -en el punto\((0,−5)\). El\(y\) -intercepto es\((0,−5)\).
Encuentra las\(y\) intercepciones\(x\) - y -en la gráfica.
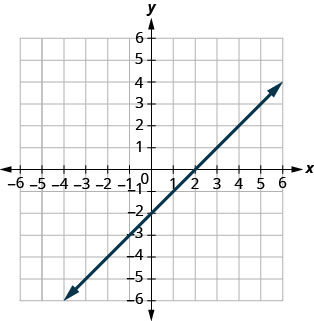
- Contestar
-
\(x\)-interceptar:\((2,0)\),
\(y\) -interceptar:\((0,−2)\)
Encuentra las\(y\) intercepciones\(x\) - y -en la gráfica.
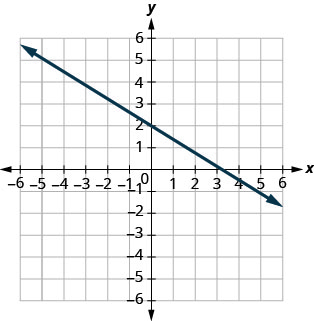
- Contestar
-
\(x\)-interceptar:\((3,0)\),
\(y\) -interceptar:\((0,2)\)
Al reconocer que la\(x\) -intercepción ocurre cuando\(y\) es cero y que la\(y\) -intercepción ocurre cuando\(x\) es cero, nos da un método para encontrar las intercepciones de una línea a partir de su ecuación. Para encontrar la\(x\) -intercepción, vamos\(y=0\) and solve for\(x.\) Para encontrar la\(y\) -intercepción, vamos\(x=0\) and solve for\(y.\)
Usa la ecuación de la línea. Para encontrar:
- la\(x\) -intercepción de la línea, dejar\(y=0\) y resolver para\(x\).
- la\(y\) -intercepción de la línea, dejar\(x=0\) y resolver para\(y\).
Encuentra las intercepciones de\(2x+y=8\).
Solución:
Vamos\(y=0\) a dejar para encontrar la\(x\) -intercepción, y vamos\(x=0\) a encontrar la\(y\) -intercepción. Llenaremos una tabla, que nos recuerda lo que necesitamos encontrar.

| Para encontrar la\(x\) -intercepción, vamos\(y=0\). | |
| \(2x+y=8\) | |
| Vamos\(y=0\). | \(2x+{\color{red}0}=8\) |
| Simplificar. | \(2x=8\) |
| \(x=4\) | |
| La\(x\) -intercepción es: | \((4,0)\) |
| Para encontrar la\(y\) -intercepción, vamos\(x=0\). | |
| \(2x+y=8\) | |
| Vamos\(x=0\). | \(2 ( {\color{red}0}) + y = 8\) |
| Simplificar. | \(0 + y = 8\) |
| \(y=8\) | |
| La\(y\) -intercepción es: | \((0,8)\) |
Los interceptos son los puntos\((4,0)\) y\((0,8)\) como se muestra en la tabla.
| \(2x+y=8\) | |
| \(x\) | \(y\) |
| 4 | 0 |
| 0 | 8 |
Encuentra las intercepciones:\(3x+y=12\).
- Contestar
-
\(x\)-interceptar:\((4,0)\),
\(y\) -interceptar:\((0,12)\)
Encuentra las intercepciones:\(x+4y=8\).
- Contestar
-
\(x\)-interceptar:\((8,0)\),
\(y\) -interceptar:\((0,2)\)
Graficar una Línea Usando las Intercepciones
Para graficar una ecuación lineal trazando puntos, es necesario encontrar tres puntos cuyas coordenadas sean soluciones a la ecuación. Puedes usar las intercepciones x e y como dos de tus tres puntos. Encuentra las intercepciones y luego encuentra un tercer punto para garantizar la precisión. Asegúrese de que los puntos se alineen hacia arriba y luego dibuje la línea. Este método suele ser la forma más rápida de graficar una línea.
Gráfica\(–x+2y=6\) usando las intercepciones.
Solución:



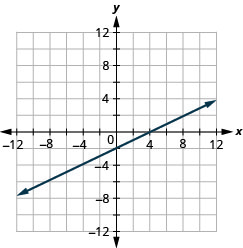
Gráfica usando las intercepciones:\(x–2y=4\).
- Contestar
-
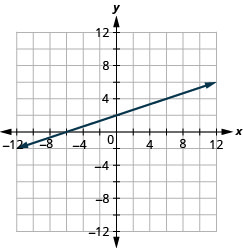
Gráfica usando las intercepciones:\(–x+3y=6\).
- Contestar
-
Aquí se resumen los pasos para graficar una ecuación lineal usando las intercepciones.
- Encuentra las\(x\) - y\(y\) -intercepciones de la línea.
- Deje y=0y=0 y resuelva para\(x\).
- Deje x=0x=0 y resuelva para\(y\).
- Encuentra una tercera solución a la ecuación.
- Trazar los tres puntos y verificar que se alineen.
- Dibuja la línea.
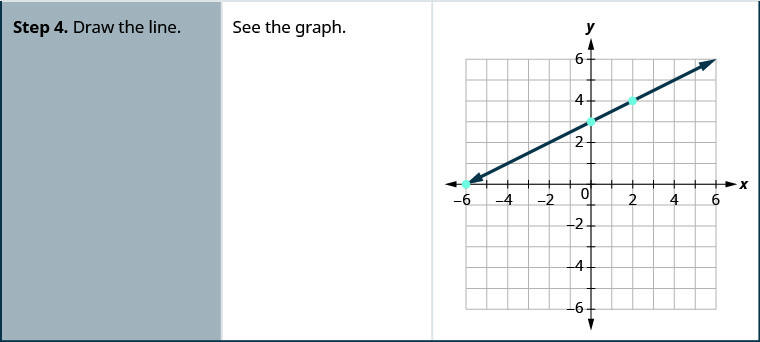
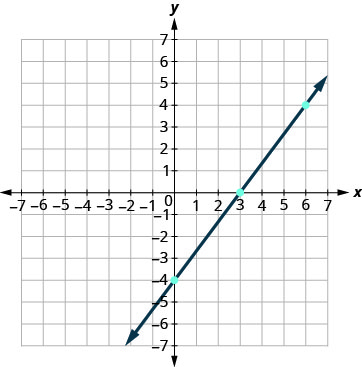
Gráfica\(4x−3y=12\) usando las intercepciones.
Solución:
Encuentra las intercepciones y un tercer punto.
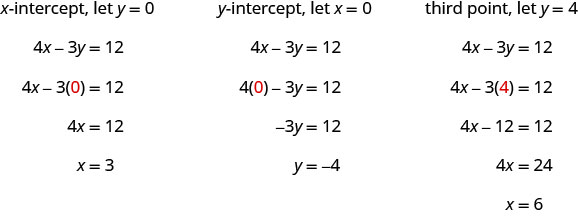
Enumeramos los puntos en la tabla y mostramos la gráfica.
| \(4x−3y=12\) | ||
| \(x\) | \(y\) | \((x,y)\) |
| 3 | 0 | \((3,0)\) |
| 0 | \(−4\) | \((0,−4)\) |
| 6 | 4 | \((6,4)\) |
Gráfica usando las intercepciones:\(5x−2y=10\).
- Contestar
-
Gráfica usando las intercepciones:\(3x−4y=12\).
- Contestar
-
Cuando la línea pasa por el origen, la\(x\) -intercepción y la\(y\) -intercepción son el mismo punto.
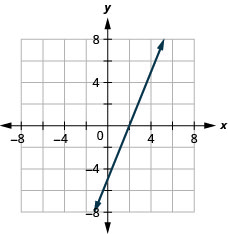
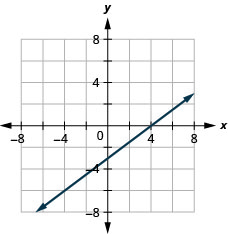
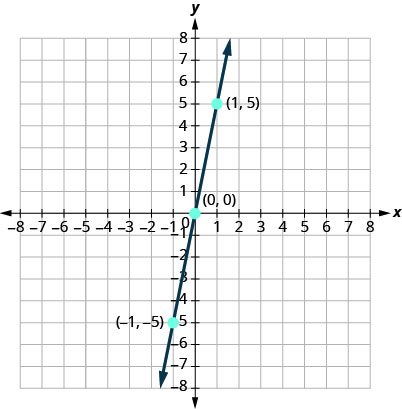
Gráfica\(y=5x\) usando las intercepciones.
Solución:

Esta línea tiene sólo una interceptación. Es el punto\((0,0)\).
Para garantizar la precisión, necesitamos trazar tres puntos. Dado que las\(y\) intercepciones\(x\) - y -son el mismo punto, necesitamos dos puntos más para graficar la línea.
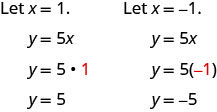
Los tres puntos resultantes se resumen en la tabla.
| \(y=5x\) | ||
| \(x\) | \(y\) | \((x,y)\) |
| 0 | 0 | \((0,0)\) |
| 1 | 5 | \((1,5)\) |
| \(−1\) | \(−5\) | \((−1,−5)\) |
Trace los tres puntos, verifique que se alineen y dibuje la línea.
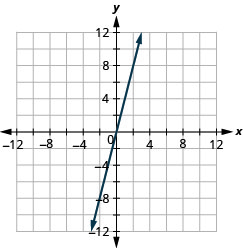
Gráfica usando las intercepciones:\(y=4x\).
- Contestar
-
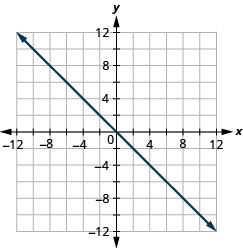
Grafica las intercepciones:\(y=−x\).
- Contestar
-
Conceptos clave
- Puntos en los Ejes
- Los puntos con una\(y\) coordenada -igual a\(0\) están en el\(x\) eje -y tienen coordenadas\((a,0)\).
- Los puntos con una\(x\) coordenada -igual a\(0\) están en el\(y\) eje -y tienen coordenadas\((0,b)\).
- Cuadrante
Cuadrante I Cuadrante II Cuadrante III Cuadrante IV \((x,y)\) \((x,y)\) \((x,y)\) \((x,y)\) \((+,+)\) \((-,+)\) \((-,-)\) \((+,-)\) 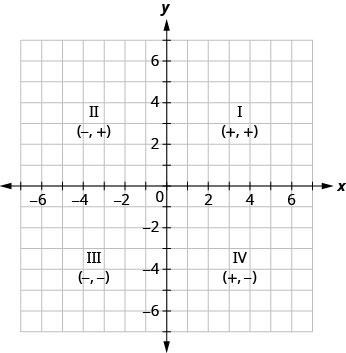
- Gráfica de una Ecuación Lineal: La gráfica de una ecuación lineal\(Ax+By=C\) es una línea recta.
Cada punto de la línea es una solución de la ecuación.
Toda solución de esta ecuación es un punto en esta línea. - Cómo graficar una ecuación lineal trazando puntos.
- Encuentra tres puntos cuyas coordenadas son soluciones a la ecuación. Organizarlos en una mesa.
- Trazar los puntos en un sistema de coordenadas rectangulares. Comprueba que los puntos se alineen. Si no lo hacen, revisa cuidadosamente tu trabajo.
- Dibuja la línea a través de los tres puntos. Extiende la línea para llenar la cuadrícula y coloca flechas en ambos extremos de la línea.
- \(x\)-intercepción e\(y\) -intercepción de una Línea
- La\(x\) intersección es el punto\((a,0)\) donde la línea cruza el\(x\) eje.
- La\(y\) intersección es el punto\((0,b)\) donde la línea cruza el\(y\) eje.

- Encuentra las\(y\) intercepciones\(x\) - y -de la ecuación de una línea
- Usa la ecuación de la línea. Para encontrar:
la\(x\) -intercepción de la línea, dejar\(y=0\) y resolver para\(x.\)
la\(y\) -intercepción de la línea, dejar\(x=0\) y resolver para\(y.\)
- Usa la ecuación de la línea. Para encontrar:
- Cómo graficar una ecuación lineal usando las intercepciones.
- Encuentra las\(x\) - y\(y\) -intercepciones de la línea.
Deje\(y=0\) y resuelva para\(x.\)
Let\(x=0\) y solucione para\(y.\) - Encuentra una tercera solución a la ecuación.
- Trazar los tres puntos y verificar que se alineen.
- Dibuja la línea.
- Encuentra las\(x\) - y\(y\) -intercepciones de la línea.
Glosario
- línea horizontal
- Una línea horizontal es la gráfica de una ecuación de la forma\(y=b.\) La línea pasa a través del\(y\) eje -en\((0,b).\)
- intercepciones de una línea
- Los puntos donde una línea cruza el\(x\) eje y el\(y\) eje -se denominan las intercepciones de la línea.
- ecuación lineal
- Una ecuación de la forma\(Ax+By=C,\) donde\(A\) y no\(B\) son ambos cero, se denomina ecuación lineal en dos variables.
- par ordenado
- Un par ordenado,\((x,y),\) da las coordenadas de un punto en un sistema de coordenadas rectangular. El primer número es la\(x\) coordenada. El segundo número es la\(y\) coordenada.
- origen
- Al punto\((0,0)\) se le llama el origen. Es el punto donde se cruzan los\(x\) ejes\(y\) -axis y -axis.
- solución de una ecuación lineal en dos variables
- Un par ordenado\((x,y)\) es una solución de la ecuación lineal\(Ax+By=C,\) si la ecuación es una declaración verdadera cuando los\(y\) valores\(x\) - y -del par ordenado se sustituyen en la ecuación.
- forma estándar de una ecuación lineal
- Una ecuación lineal está en forma estándar cuando se escribe\(Ax+By=C.\)
- línea vertical
- Una línea vertical es la gráfica de una ecuación de la forma\(x=a.\) La línea pasa a través del\(x\) eje -en\((a,0).\)


