3.5E: Ejercicios

Última actualización
Guardar como PDF

Page ID: 112266

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

La práctica hace la perfección

Verificar soluciones a una desigualdad en dos variables

En los siguientes ejercicios, determinar si cada par ordenado es una solución a la desigualdad dada.

1. Determine si cada par ordenado es una solución a la desigualdad$y>x−1$:

a.$(0,1)$
b.$(−4,−1)$
c.$(4,2)$
d.$(3,0)$
e.$(−2,−3)$

Contestar: a. si b. si c. no d. no e. no

2. Determine si cada par ordenado es una solución a la desigualdad$y>x−3$:

a.$(0,0)$
b.$(2,1)$
c.$(−1,−5)$
d.$(−6,−3)$
e.$(1,0)$

3. Determine si cada par ordenado es una solución a la desigualdad$y<3x+2$:

a.$(0,3)$
b.$(−3,−2)$
c.$(−2,0)$
d.$(0,0)$
e.$(−1,4)$

Contestar: a. no b. no c. si d. si e. no

4. Determine si cada par ordenado es una solución a la desigualdad$y<−2x+5$:

a.\ ((−3,0) (−3,0)
b.$(1,6)$
c.$(−6,−2)$
d.$(0,1)$
e.$(5,−4)$

5. Determine si cada par ordenado es una solución a la desigualdad$3x−4y>4$:

a.$(5,1)$
b.$(−2,6)$
c.$(3,2)$
d.$(10,−5)$
e.$(0,0)$

Contestar: a. si b. no c. no d. no e. no

6. Determine si cada par ordenado es una solución a la desigualdad$2x+3y>2$:

a.$(1,1)$
b.$(4,−3)$
c.$(0,0)$
d.$(−8,12)$
e.$(3,0)$

Reconocer la relación entre las soluciones de una desigualdad y su gráfica

En los siguientes ejercicios, escriba la desigualdad mostrada por la región sombreada.

7. Escribe la desigualdad que muestra la gráfica con la línea límite$y=3x−4$.

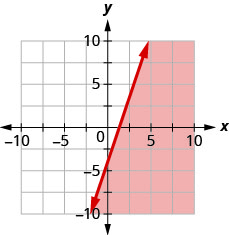
$Esta figura tiene la gráfica de una línea recta en el plano de la coordenada x y. Los ejes x e y van de negativo 10 a 10. Se dibuja una línea a través de los puntos (0, negativo 4), (1, negativo 1) y (2, 2). La línea divide el plano de la coordenada x y en dos mitades. La línea y la mitad inferior derecha están sombreadas en rojo para indicar que aquí es donde están las soluciones de la desigualdad.$

Contestar: $y\leq 3x−4$

8. Escribe la desigualdad que muestra la gráfica con la línea límite$y=2x−4$.

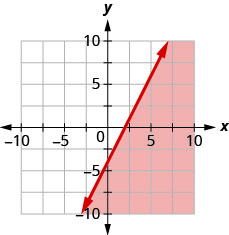
$Esta figura tiene la gráfica de una línea recta en el plano de la coordenada x y. Los ejes x e y van de negativo 10 a 10. Se dibuja una línea a través de los puntos (0, negativo 4), (1, negativo 2) y (2, 0). La línea divide el plano de la coordenada x y en dos mitades. La línea y la mitad inferior derecha están sombreadas en rojo para indicar que aquí es donde están las soluciones de la desigualdad.$

9. Escribe la desigualdad que muestra la gráfica con la línea límite$y=−\frac{1}{2}x+1$.

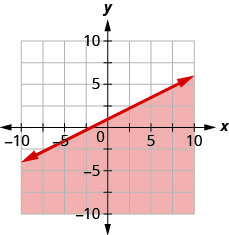
$Esta figura tiene la gráfica de una línea recta en el plano de la coordenada x y. Los ejes x e y van de negativo 10 a 10. Se dibuja una línea a través de los puntos (0, 1), (2, 0) y (4, negativo 1). La línea divide el plano de la coordenada x y en dos mitades. La línea y la mitad inferior derecha están sombreadas en rojo para indicar que aquí es donde están las soluciones de la desigualdad.$

Contestar: $y\leq −\frac{1}{2}x+1$

10. Escribe la desigualdad que muestra la gráfica con la línea límite$y=-\frac{1}{3}x−2$.

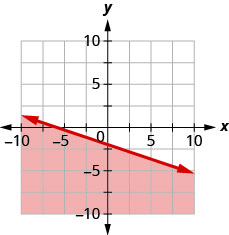
$Esta figura tiene la gráfica de una línea recta en el plano de la coordenada x y. Los ejes x e y van de negativo 10 a 10. Se dibuja una línea a través de los puntos (0, negativo 2), (3, negativo 3) y (6, negativo 4). La línea divide el plano de la coordenada x y en dos mitades. La línea y la mitad inferior izquierda están sombreadas en rojo para indicar que aquí es donde están las soluciones de la desigualdad.$

11. Escribe la desigualdad que muestra la región sombreada en la gráfica con la línea límite$x+y=5$.

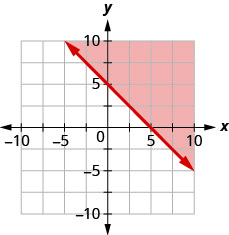
$Esta figura tiene la gráfica de una línea recta en el plano de la coordenada x y. Los ejes x e y van de negativo 10 a 10. Se dibuja una línea a través de los puntos (0, 5), (1, 4) y (5, 0). La línea divide el plano de la coordenada x y en dos mitades. La línea y la mitad superior derecha están sombreadas en rojo para indicar que aquí es donde están las soluciones de la desigualdad.$

Contestar: $x+y\geq 5$

12. Escribe la desigualdad que muestra la región sombreada en la gráfica con la línea límite$x+y=3$.

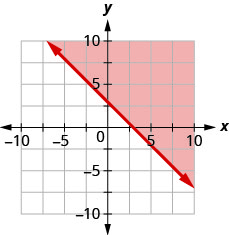
$Esta figura tiene la gráfica de una línea recta en el plano de la coordenada x y. Los ejes x e y van de negativo 10 a 10. Se dibuja una línea a través de los puntos (0, 3), (1, 2) y (3, 0). La línea divide el plano de la coordenada x y en dos mitades. La línea y la mitad superior derecha están sombreadas en rojo para indicar que aquí es donde están las soluciones de la desigualdad.$

13. Escribe la desigualdad que muestra la región sombreada en la gráfica con la línea límite$3x−y=6$.

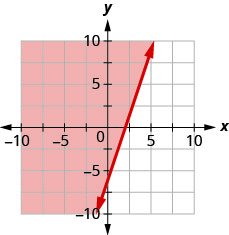
$Esta figura tiene la gráfica de una línea recta en el plano de la coordenada x y. Los ejes x e y van de negativo 10 a 10. Se dibuja una línea a través de los puntos (0, negativo 6), (1, negativo 3) y (2, 0). La línea divide el plano de la coordenada x y en dos mitades. La línea y la mitad superior izquierda están sombreadas en rojo para indicar que aquí es donde están las soluciones de la desigualdad.$

Contestar: $3x−y\leq 6$

14. Escribe la desigualdad que muestra la región sombreada en la gráfica con la línea límite$2x−y=4$.

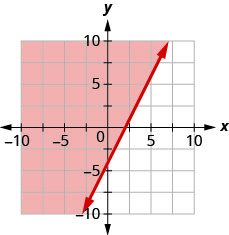
$Esta figura tiene la gráfica de una línea recta en el plano de la coordenada x y. Los ejes x e y van de negativo 10 a 10. Se dibuja una línea a través de los puntos (0, negativo 4), (1, negativo 2) y (2, 0). La línea divide el plano de la coordenada x y en dos mitades. La línea y la mitad superior izquierda están sombreadas en rojo para indicar que aquí es donde están las soluciones de la desigualdad.$

Graficar desigualdades lineales en dos variables

En los siguientes ejercicios, grafica cada desigualdad lineal.

15. Grafica la desigualdad lineal:$y>\frac{2}{3}x−1$.

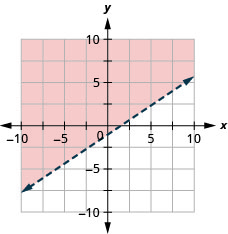
Contestar: $Esta figura tiene la gráfica de una línea discontinua recta en el plano de la coordenada x y. Los ejes x e y van de negativo 10 a 10. Se dibuja una línea discontinua recta a través de los puntos (0, negativo 1), (3, 1) y (6, 3). La línea divide el plano de la coordenada x y en dos mitades. La mitad superior izquierda está sombreada en rojo para indicar que aquí es donde están las soluciones de la desigualdad.$

16. Grafica la desigualdad lineal:$y<\frac{3}{5}x+2$.

17. Grafica la desigualdad lineal:$y\leq −\frac{1}{2}x+4$.

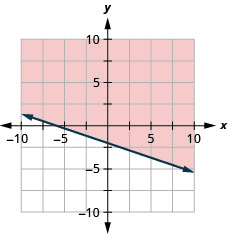
Contestar: $Esta figura tiene la gráfica de una línea recta en el plano de la coordenada x y. Los ejes x e y van de negativo 10 a 10. Se dibuja una línea a través de los puntos (0, 4), (2, 3) y (4, 2). La línea divide el plano de la coordenada x y en dos mitades. La línea y la mitad superior derecha están sombreadas en rojo para indicar que aquí es donde están las soluciones de la desigualdad.$

18. Grafica la desigualdad lineal:$y\geq −\frac{1}{3}x−2$.

19. Grafica la desigualdad lineal:$x−y\leq 3$.

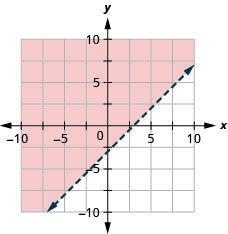
Contestar: $Esta figura tiene la gráfica de una línea discontinua recta en el plano de la coordenada x y. Los ejes x e y van de negativo 10 a 10. Se dibuja una línea discontinua recta a través de los puntos (0, negativo 3), (1, negativo 2) y (3, 0). La línea divide el plano de la coordenada x y en dos mitades. La mitad superior izquierda está sombreada en rojo para indicar que aquí es donde están las soluciones de la desigualdad.$

20. Grafica la desigualdad lineal:$x−y\geq −2$.

21. Grafica la desigualdad lineal:$4x+y>−4$.

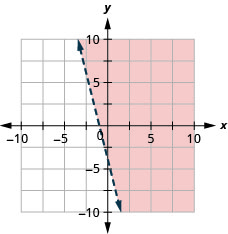
Contestar: $Esta figura tiene la gráfica de una línea discontinua recta en el plano de la coordenada x y. Los ejes x e y van de negativo 10 a 10. Se dibuja una línea discontinua recta a través de los puntos (0, negativo 4), (negativo 1, 0) y (1, negativo 8). La línea divide el plano de la coordenada x y en dos mitades. La mitad superior derecha está sombreada en rojo para indicar que aquí es donde están las soluciones de la desigualdad.$

22. Grafica la desigualdad lineal:$x+5y<−5$.

23. Grafica la desigualdad lineal:$3x+2y\geq −6$.

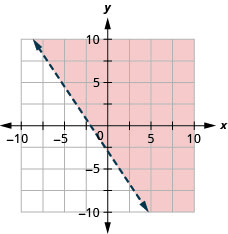
Contestar: $Esta figura tiene la gráfica de una línea discontinua recta en el plano de la coordenada x y. Los ejes x e y van de negativo 10 a 10. Se dibuja una línea discontinua recta a través de los puntos (0, negativo 3), (3, negativo 5) y (negativo 2, 0). La línea divide el plano de la coordenada x y en dos mitades. La mitad superior derecha está sombreada en rojo para indicar que aquí es donde están las soluciones de la desigualdad.$

24. Grafica la desigualdad lineal:$4x+2y\geq −8$.

25. Grafica la desigualdad lineal:$y>4x$.

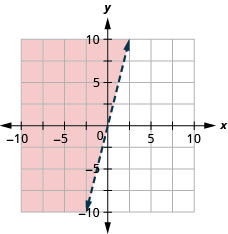
Contestar: $Esta figura tiene la gráfica de una línea discontinua recta en el plano de la coordenada x y. Los ejes x e y van de negativo 10 a 10. Se dibuja una línea discontinua recta a través de los puntos (0, 0), (negativo 1, negativo 4) y (1, 4). La línea divide el plano de la coordenada x y en dos mitades. La mitad superior izquierda está sombreada en rojo para indicar que aquí es donde están las soluciones de la desigualdad.$

26. Grafica la desigualdad lineal:$y\leq −3x$.

27. Grafica la desigualdad lineal:$y<−10$.

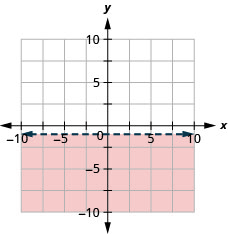
Contestar: $Esta figura tiene la gráfica de una línea discontinua recta en el plano de la coordenada x y. Los ejes x e y van de negativo 10 a 10. Se dibuja una línea discontinua recta a través de los puntos (0, 0), (negativo 1, 3) y (1, negativo 3). La línea divide el plano de la coordenada x y en dos mitades. La mitad inferior izquierda está sombreada en rojo para indicar que aquí es donde están las soluciones de la desigualdad.$

28. Grafica la desigualdad lineal:$y\geq 2$.

29. Grafica la desigualdad lineal:$x\leq 5$.

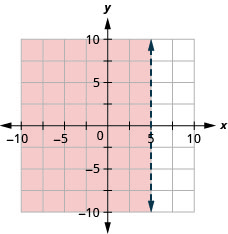
Contestar: $Esta figura tiene la gráfica de una línea discontinua vertical recta en el plano de la coordenada x y. Los ejes x e y van de negativo 10 a 10. Se dibuja una línea discontinua vertical a través de los puntos (5, negativo 1), (5, 0) y (5, 1). La línea divide el plano de la coordenada x y en dos mitades. La mitad izquierda está sombreada en rojo para indicar que aquí es donde están las soluciones de la desigualdad.$

30. Grafica la desigualdad lineal:$x\geq 0$.

31. Grafica la desigualdad lineal:$x−y<4$.

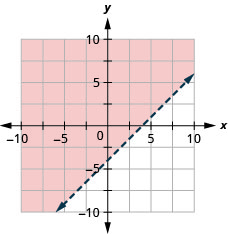
Contestar: $Esta figura tiene la gráfica de una línea discontinua recta en el plano de la coordenada x y. Los ejes x e y van de negativo 10 a 10. Se dibuja una línea discontinua recta a través de los puntos (0, negativo 4), (1, negativo 3) y (4, 0). La línea divide el plano de la coordenada x y en dos mitades. La mitad superior izquierda está sombreada en rojo para indicar que aquí es donde están las soluciones de la desigualdad.$

32. Grafica la desigualdad lineal:$x−y<−3$.

33. Grafica la desigualdad lineal:$y\geq \frac{3}{2}x$.

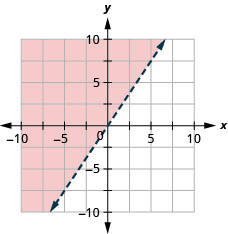
Contestar: $Esta figura tiene la gráfica de una línea discontinua recta en el plano de la coordenada x y. Los ejes x e y van de negativo 10 a 10. Se dibuja una línea discontinua recta a través de los puntos (0, 0), (2, 3) y (negativo 2, negativo 3). La línea divide el plano de la coordenada x y en dos mitades. La mitad superior izquierda está sombreada en rojo para indicar que aquí es donde están las soluciones de la desigualdad.$

34. Grafica la desigualdad lineal:$y\leq \frac{5}{4}x$.

35. Grafica la desigualdad lineal:$y>−2x+1$.

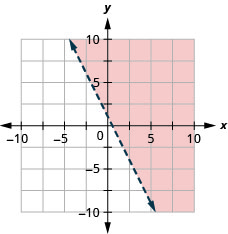
Contestar: $Esta figura tiene la gráfica de una línea discontinua recta en el plano de la coordenada x y. Los ejes x e y van de negativo 10 a 10. Se dibuja una línea discontinua recta a través de los puntos (0, 1), (1, negativo 1) y (2, negativo 3). La línea divide el plano de la coordenada x y en dos mitades. La mitad superior derecha está sombreada en rojo para indicar que aquí es donde están las soluciones de la desigualdad.$

36. Grafica la desigualdad lineal:$y<−3x−4$.

37. Grafica la desigualdad lineal:$2x+y\geq −4$.

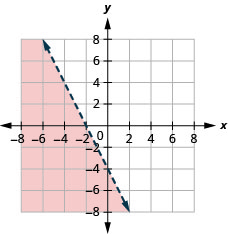
Contestar: $Esta figura tiene la gráfica de una línea recta en el plano de la coordenada x y. Los ejes x e y van de negativo 10 a 10. Se dibuja una línea a través de los puntos (0, negativo 4), (1, negativo 6) y (negativo 2, 0). La línea divide el plano de la coordenada x y en dos mitades. La línea y la mitad inferior izquierda están sombreadas en rojo para indicar que aquí es donde están las soluciones de la desigualdad.$

38. Grafica la desigualdad lineal:$x+2y\leq −2$.

39. Grafica la desigualdad lineal:$2x−5y>10$.

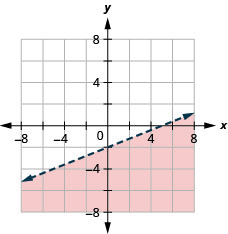
Contestar: $Esta figura tiene la gráfica de una línea recta en el plano de la coordenada x y. Los ejes x e y van de negativo 10 a 10. Se dibuja una línea a través de los puntos (0, negativo 2), (5, 0) y (negativo 5, negativo 4). La línea divide el plano de la coordenada x y en dos mitades. La línea y la mitad inferior derecha están sombreadas en rojo para indicar que aquí es donde están las soluciones de la desigualdad.$

40. Grafica la desigualdad lineal:$4x−3y>12$.

Resolver aplicaciones usando desigualdades lineales en dos variables

41. Harrison trabaja en dos trabajos a tiempo parcial. Uno en una gasolinera que paga $11 la hora y el otro es la solución de problemas de TI por $16.50$16.50la hora. Entre los dos trabajos, Harrison quiere ganar al menos 330 dólares a la semana. ¿Cuántas horas necesita Harrison para trabajar en cada trabajo para ganar al menos $330?

a. dejar x ser el número de horas que trabaja en la gasolinera y dejar que y sea el número de (horas que trabaja solución de problemas. Escribir una desigualdad que modelaría esta situación.

b. Graficar la desigualdad.

c. Encontrar tres pares ordenados$(x,y)$ que serían soluciones a la desigualdad. Entonces, explica lo que eso significa para Harrison.

Contestar

a.$11x+16.5y\geq 330$
b.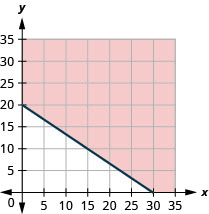

$Esta figura tiene la gráfica de una línea recta en el plano de la coordenada x y. Los ejes x e y van de 0 a 35. Se dibuja una línea a través de los puntos (0, 20), (15, 10) y (30, 0). La línea divide el plano de la coordenada x y en dos mitades. La línea y la mitad superior derecha están sombreadas en rojo para indicar que aquí es donde están las soluciones de la desigualdad.$

c. Las respuestas variarán.

42. Elena necesita ganar al menos 450 dólares a la semana durante sus vacaciones de verano para pagar la universidad. Ella trabaja en dos trabajos. Uno como instructor de natación que paga $9 la hora y el otro como pasante en un laboratorio de genética por $22.50 por hora. ¿Cuántas horas necesita Elena para trabajar en cada trabajo para ganar al menos 450 dólares semanales?

a. Que x sea el número de horas que trabaja enseñando natación y que sea el número de horas que trabaja como pasante. Escribir una desigualdad que modelaría esta situación.

b. Graficar la desigualdad.

c. Encontrar tres pares ordenados (x, y) (x, y) que serían soluciones a la desigualdad. Entonces, explica lo que eso significa para Elena.

43. El médico le dice a Laura que necesita hacer ejercicio lo suficiente para quemar 500 calorías cada día. Prefiere correr o andar en bicicleta y quema 15 calorías por minuto mientras corre y 10 calorías por minuto mientras anda en bicicleta.

a. si x es el número de minutos que corre Laura e y es el número de minutos que bija, encuentra la desigualdad que modela la situación.

b. Graficar la desigualdad.

c. Enumerar tres soluciones a la desigualdad. ¿Qué opciones ofrecen las soluciones Laura?

Contestar

a.$15x+10y\geq 500$
b.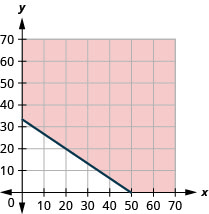

$Esta figura tiene la gráfica de una línea recta en el plano de la coordenada x y. Los ejes x e y van de 0 a 60. Se dibuja una línea a través de los puntos (0, 50) y (20, 20). La línea divide el plano de la coordenada x y en dos mitades. La línea y la mitad superior derecha están sombreadas en rojo para indicar que aquí es donde están las soluciones de la desigualdad.$

c. Las respuestas variarán.

44. Los entrenamientos de Armando consisten en kickboxing y natación. Mientras que kickboxing, quema 10 calorías por minuto y quema 7 calorías por minuto mientras nada. Quiere quemar 600 calorías cada día.

a. si x es el número de minutos que Armando hará kickbox e y es el número de minutos que va a nadar, encuentra la desigualdad que ayudará a Armando a crear un entrenamiento para hoy.

b. Graficar la desigualdad.

c. Enumerar tres soluciones a la desigualdad. ¿Qué opciones ofrecen las soluciones Armando?

Ejercicios de escritura

45. Lester piensa que la solución de cualquier desigualdad con un signo >> es la región por encima de la línea y la solución de cualquier desigualdad con un signo << es la región debajo de la línea. ¿Lester es correcto? Explique por qué o por qué no.

Contestar: Las respuestas variarán.

46. Explique por qué, en algunas gráficas de desigualdades lineales, la línea límite es sólida pero en otras gráficas es discontinua.

Autocomprobación

a. después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.

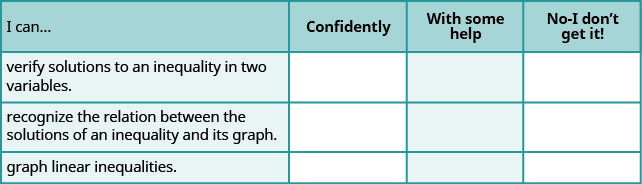
$Esta tabla tiene 4 filas y 4 columnas. La primera fila es una fila de encabezado y etiqueta cada columna. El encabezado de la primera columna es “Puedo...”, el segundo es “Con confianza”, el tercero es “Con algo de ayuda”, y el cuarto es “No, no lo entiendo”. Bajo la primera columna se encuentran las frases “verificar soluciones a una desigualdad en dos variables”, “reconocer la relación entre las soluciones de una desigualdad y su gráfica”, y “graficar desigualdades lineales”. Las otras columnas se dejan en blanco para que el alumno pueda indicar su nivel de dominio para cada tema.$

b. En una escala del 1 al 10, ¿cómo calificaría su dominio de esta sección a la luz de sus respuestas en la lista de verificación? ¿Cómo se puede mejorar esto?

Search

Text Color

Text Size

Margin Size

Font Type