3.6E: Ejercicios

Última actualización
Guardar como PDF

Page ID: 112324

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

La práctica hace la perfección

Encontrar el dominio y el rango de una relación

En los siguientes ejercicios, para cada relación a. encontrar el dominio de la relación b. encontrar el rango de la relación.

1. ${\{(1,4),(2,8),(3,12),(4,16),(5,20)}\}$

Responder: a.${\{1, 2, 3, 4, 5}\}$ b.${\{4, 8, 12, 16, 20}\}$

2. ${\{(1,−2),(2,−4),(3,−6),(4,−8),(5,−10)}\}$

3. ${\{(1,7),(5,3),(7,9),(−2,−3),(−2,8)}\}$

Responder: a.${\{1, 5, 7, −2}\}$ b.${\{7, 3, 9, −3, 8}\}$

4. ${\{(11,3),(−2,−7),(4,−8),(4,17),(−6,9)}\}$

En los siguientes ejercicios, utilice el mapeo de la relación con a. enumerar los pares ordenados de la relación, b. encontrar el dominio de la relación, y c. encontrar el rango de la relación.

5.
$Esta figura muestra dos tablas que cada una tiene una columna. La mesa de la izquierda tiene el encabezado “Nombre” y enumera los nombres “Rebecca”, “Jennifer”, “John”, “Héctor”, “Luis”, “Ebony”, “Raphael”, “Meredith”, “Karen”, y “Joseph”. El cuadro de la derecha tiene el encabezado “Cumpleaños” y enumera las fechas “18 de enero”, “15 de febrero”, “1 de abril”, “7 de abril”, “23 de junio”, “30 de julio”, “19 de agosto” y “6 de noviembre”. Hay flechas que comienzan en los nombres en la tabla Nombre y que apuntan hacia las fechas en la tabla Cumpleaños. La primera flecha va de Rebecca al 18 de enero. La segunda flecha va de Jennifer al 1 de abril. La tercera flecha va de Juan al 18 de enero. La cuarta flecha va de Héctor al 23 de junio. La quinta flecha va de Luis al 15 de febrero. La sexta flecha va de Ébano al 7 de abril. La séptima flecha va de Rafael al 6 de noviembre. La octava flecha va de Meredith al 19 de agosto. La novena flecha va de Karen al 19 de agosto. La décima flecha va de José al 30 de julio.$

Responder: a. (Rebecca, 18 de enero), (Jennifer, 1 de abril), (John, 18 de enero), (Héctor, 23 de junio), (Luis, 15 de febrero), (Ébano, 7 de abril), (Rafael, 6 de noviembre), (Meredith, 19 de agosto), (Karen, 19 de agosto), (José, 30 de julio)
b. {Rebecca, Jennifer, John, Héctor, Luis, Ébano, Rafael, Edith, Karen, José}
c. {18 de enero, 1 de abril, 23 de junio, 15 de febrero, 7 de abril, 6 de noviembre, 19 de agosto, 30 de julio}

6.
$Esta figura muestra dos tablas que cada una tiene una columna. La tabla de la izquierda tiene el encabezado “Nombre” y enumera los nombres “Amy”, “Carol”, “Devon”, “Harrison”, “Jackson”, “Labron”, “Mason”, “Natalie”, “Paul”, y “Sylvester”. El cuadro de la derecha tiene el encabezado “Cumpleaños” y enumera las fechas “5 de enero”, “7 de enero”, “14 de febrero”, “1 de marzo”, “7 de abril”, “30 de mayo”, “20 de julio”, “1 de agosto”, “13 de noviembre” y “26 de noviembre”. Hay flechas que comienzan en los nombres en la tabla Nombre y que apuntan hacia las fechas en la tabla Cumpleaños. La primera flecha va de Amy al 14 de febrero. La segunda flecha va de Carol al 30 de mayo. La tercera flecha va de Devon al 5 de enero. La cuarta flecha va de Harrison al 7 de enero. La quinta flecha va de Jackson al 26 de noviembre. La sexta flecha va de Labron al 7 de abril. La séptima flecha va de Mason al 20 de julio. La octava flecha va de Natalie al 1 de marzo. La novena flecha va de Pablo al 1 de agosto. La décima flecha va de Sylvester al 13 de noviembre.$

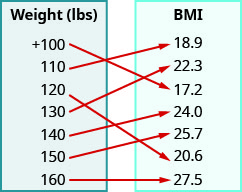
7. Para una mujer de estatura$5'4''$ el siguiente mapeo muestra el Índice de Masa Corporal (IMC) correspondiente. El índice de masa corporal es una medición de la grasa corporal basada en la estatura y el peso. Un IMC de$18.5–24.9$ se considera saludable.

$Esta figura muestra dos tablas que cada una tiene una columna. La tabla de la izquierda tiene el encabezado “Peso (lbs)” y enumera los números más 100, 110, 120, 130, 140, 150 y 160. El cuadro de la derecha tiene el encabezado “IMC” y enumera los números 18. 9, 22. 3, 17. 2, 24. 0, 25. 7, 20. 6, y 27. 5. Hay flechas que comienzan en números en la tabla de pesos y apuntando hacia los números en la tabla de IMC. La primera flecha va de más 100 a 17. 2. La segunda flecha va del 110 al 18. 9. La tercera flecha va de 120 a 20. 6. La cuarta flecha va de 130 a 22. 3. La quinta flecha va de 140 a 24. 0. La sexta flecha va de 150 a 25. 7. La séptima flecha va de 160 a 27. 5.$

Responder: a.$(+100, 17. 2), (110, 18.9), (120, 20.6), (130, 22.3), (140, 24.0), (150, 25.7), (160, 27.5)$ b.${\{+100, 110, 120, 130, 140, 150, 160,}\}$ c.${\{17.2, 18.9, 20.6, 22.3, 24.0, 25.7, 27.5}\}$

8. Para un hombre de estatura$5'11''$ el siguiente mapeo muestra el Índice de Masa Corporal (IMC) correspondiente. El índice de masa corporal es una medición de la grasa corporal basada en la estatura y el peso. Un IMC de$18.5–24.9$ se considera saludable.

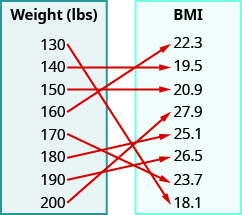
$Esta figura muestra dos tablas que cada una tiene una columna. La tabla de la izquierda tiene el encabezado “Peso (lbs)” y enumera los números 130, 140, 150, 160, 170, 180, 190 y 200. El cuadro de la derecha tiene el encabezado “IMC” y enumera los números 22. 3, 19. 5, 20. 9, 27. 9, 25. 1, 26. 5, 23. 7, y 18. 1. Hay flechas que comienzan en números en la tabla de pesos y apuntando hacia los números en la tabla de IMC. La primera flecha va de 130 a 18. 1. La segunda flecha va de 140 a 19. 5. La tercera flecha va de 150 a 20. 9. La cuarta flecha va de 160 a 22. 3. La quinta flecha va de 170 a 23. 7. La sexta flecha va de 180 a 25. 1. La séptima flecha va de 190 a 26. 5. La octava flecha va de 200 a 27. 9.$

En los siguientes ejercicios, utilice la gráfica de la relación a a. listar los pares ordenados de la relación b. encontrar el dominio de la relación c. encontrar el rango de la relación.

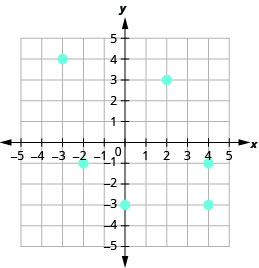
9.
$La figura muestra la gráfica de algunos puntos en el plano de la coordenada x y. Los ejes x e y van de 6 a 6 negativos. Los puntos (negativo 3, 4), (negativo 3, negativo 1), (0, negativo 3), (2, 3), (4, negativo 1), y (4, negativo 3).$

Responder: a.$(2, 3), (4, −3), (−2, −1), (−3, 4), (4, −1), (0, −3)$ b.${\{−3, −2, 0, 2, 4}\}$
c.${\{−3, −1, 3, 4}\}$

10.
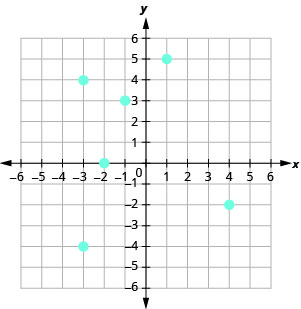
$La figura muestra la gráfica de algunos puntos en el plano de la coordenada x y. Los ejes x e y van de 6 a 6 negativos. Los puntos (negativo 3, 4), (negativo 3, negativo 4), (negativo 2, 0), (negativo 1, 3), (1, 5), y (4, negativo 2).$

11.
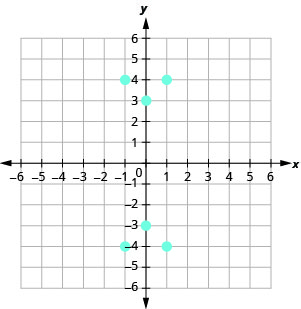
$La figura muestra la gráfica de algunos puntos en el plano de la coordenada x y. Los ejes x e y van de 6 a 6 negativos. Los puntos (negativo 1, 4), (negativo 1, negativo 4), (0, 3), (0, negativo 3), (1, 4), y (1, negativo 4).$

Responder: a.$(1, 4), (1, −4), (−1, 4), (−1, −4), (0, 3), (0, −3)$ b.${\{−1, 0, 1}\}$ c.${\{−4, −3, 3,4}\}$

12.
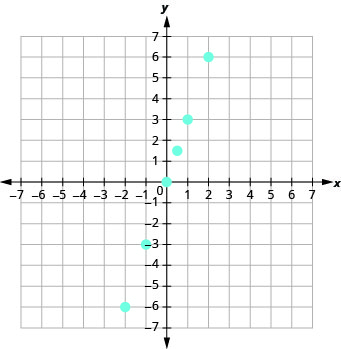
$La figura muestra la gráfica de algunos puntos en el plano de la coordenada x y. Los ejes x e y van de negativo 10 a 10. Los puntos (negativo 2, negativo 6), (negativo 2, negativo 3), (0, 0), (0. 5, 1. 5), (1, 3), y (3, 6).$

Determinar si una relación es una función

En los siguientes ejercicios, utilice el conjunto de pares ordenados para a. determinar si la relación es una función, b. encontrar el dominio de la relación, y c. encontrar el rango de la relación.

13. $ {\{(−3,9),(−2,4),(−1,1), (0,0),(1,1),(2,4),(3,9)}\}$

Responder: a. si b.${\{−3, −2, −1, 0, 1, 2, 3}\}$ c.${\{9, 4, 1, 0}\}$

14. ${\{(9,−3),(4,−2),(1,−1),(0,0),(1,1),(4,2),(9,3)}\}$

15. ${\{(−3,27),(−2,8),(−1,1), (0,0),(1,1),(2,8),(3,27)}\}$

Responder: a. si b.${\{−3, −2, −1, 0, 1, 2, 3}\}$ c.${\{0, 1, 8, 27}\}$

16. ${\{(−3,−27),(−2,−8),(−1,−1), (0,0),(1,1),(2,8),(3,27)}\}$

En los siguientes ejercicios, utilice el mapeo para a. determinar si la relación es una función, b. encontrar el dominio de la función, y c. encontrar el rango de la función.

17.
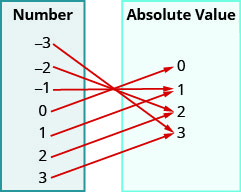
$Esta figura muestra dos tablas que cada una tiene una columna. La tabla de la izquierda tiene el encabezado “Número” y enumera los números negativos 3, negativos 2, negativos 1, 0, 1, 2 y 3. La tabla de la derecha tiene el encabezado “Valor Absoluto” y enumera los números 0, 1, 2 y 3. Hay flechas que comienzan en números en la tabla de números y que apuntan hacia los números en la tabla de valores absolutos. La primera flecha va de negativo 3 a 3. La segunda flecha va de negativo 2 a 2. La tercera flecha va de negativo 1 a 1. La cuarta flecha va de 0 a 0. La quinta flecha va de 1 a 1. La sexta flecha va de 2 a 2. La séptima flecha va de 3 a 3.$

Responder: a. si b.${\{−3, −2, −1, 0, 1, 2, 3}\}$ c.${\{0, 1, 2, 3}\}$

18.
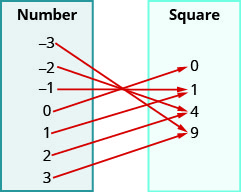
$Esta figura muestra dos tablas que cada una tiene una columna. La tabla de la izquierda tiene el encabezado “Número” y enumera los números negativos 3, negativos 2, negativos 1, 0, 1, 2 y 3. La tabla de la derecha tiene el encabezado “Cuadrado” y enumera los números 0, 1, 4 y 9. Hay flechas que comienzan en números en la tabla de números y apuntando hacia los números en la tabla cuadrada. La primera flecha va del 3 al 9 negativo. La segunda flecha va de negativo 2 a 4. La tercera flecha va de negativo 1 a 1. La cuarta flecha va de 0 a 0. La quinta flecha va de 1 a 1. La sexta flecha va de 2 a 4. La séptima flecha va del 3 al 9.$

19.
$Esta figura muestra dos tablas que cada una tiene una columna. La tabla de la izquierda tiene el encabezado “Nombre” y enumera los nombres “Jenny”, “R e y”, “Dennis”, “Emily”, y “Raúl”. La tabla de la derecha tiene el encabezado “Correo electrónico” y enumera las direcciones de correo electrónico RHern y ez @state. edu, JKim@gmail.com, Raul@gmail.com, eSmith @state. edu, DBrown@aol.com, jenny@aol.com, y R y y@gmail.com. Hay flechas que comienzan en los nombres en la tabla de nombres y que apuntan hacia las direcciones en la tabla de correo electrónico. La primera flecha va de Jenny a JKim@gmail.com. La segunda flecha va de Jenny a jenny@aol.com. La tercera flecha va de R e y a R y y@gmail.com. La cuarta flecha va de Dennis a DBrown@aol.com. La quinta flecha va de Emily a eSmith @state. edu. La sexta flecha va de Raúl a rHerN y ez @state. edu. La séptima flecha va de Raúl a Raul@gmail.com.$

Responder: a. no b. {Jenny, R e y, Dennis, Emily, Raúl} c. {rHern y ez@state.edu, JKim@gmail.com, Raul@gmail.com, ESmith@state.edu, DBroen@aol.com, jenny@aol.cvom, R y y@gmail.com}

20.
$Esta figura muestra dos tablas que cada una tiene una columna. La mesa de la izquierda tiene el encabezado “Nombre” y enumera los nombres “Jon”, “Rachel”, “Matt”, “Leslie”, “Chris”, “Beth”, y “Liz”. La tabla de la derecha tiene el encabezado “Correo electrónico” y enumera las direcciones de correo electrónico chrisg@gmail.com, lizzie@aol.com, jong@gmail.com, mattg@gmail.com, Rachel @state. edu, leslie@aol.com, y bethc@gmail.com. Hay flechas que comienzan en los nombres en la tabla de nombres y que apuntan hacia las direcciones en la tabla de correo electrónico. La primera flecha va de Jon a jong@gmail.com. La segunda flecha va de Rachel a Rachel @state. edu. La tercera flecha va de Matt a mattg@gmail.com. La cuarta flecha va de Leslie a leslie@aol.com. La quinta flecha va de Chris a chrisg@gmail.com. La sexta flecha va de Beth a bethc@gmail.com. La séptima flecha va de Liz a lizzie@aol.com.$

En los siguientes ejercicios, determine si cada ecuación es una función.

21. a.$2x+y=−3$
b.$y=x^2$
c.$x+y^2=−5$

Responder: a. si b. si c. no

22. a.$y=3x−5$
b.$y=x^3$
c.$2x+y^2=4$

23. a.$y−3x^3=2$
b.$x+y^2=3$
c.$3x−2y=6$

Responder: a. si b. no c. si

24. a.$2x−4y=8$
b.$−4=x^2−y$
c.$y^2=−x+5$

Encontrar el valor de una función

En los siguientes ejercicios, evaluar la función: a.$f(2)$ b$f(a)$.$f(−1)$ c.

25. $f(x)=5x−3$

Responder: a.$f(2)=7$ b.$f(−1)=−8$ c.$f(a)=5a−3$

26. $f(x)=3x+4$

27. $f(x)=−4x+2$

Responder: a.$f(2)=−6$ b.$f(−1)=6$ c.$f(a)=−4a+2$

28. $f(x)=−6x−3$

29. $f(x)=x^2−x+3$

Responder: a.$f(2)=5$ b.$f(−1)=5$
c.$f(a)=a^2−a+3$

30. $f(x)=x^2+x−2$

31. $f(x)=2x^2−x+3$

Responder: a.$f(2)=9$ b.$f(−1)=6$
c.$f(a)=2a^2−a+3$

32. $f(x)=3x^2+x−2$

En los siguientes ejercicios, evaluar la función: a.$g(h^2)$ b$g(x)+g(2)$.$g(x+2)$ c.

33. $g(x)=2x+1$

Responder: a.$g(h^2)=2h^2+1$
b.$g(x+2)=4x+5$
c.$g(x)+g(2)=2x+6$

34. $g(x)=5x−8$

35. $g(x)=−3x−2$

Responder: a.$g(h^2)=−3h^2−2$
b.$g(x+2)=−3x−8$
c.$g(x)+g(2)=−3x−10$

36. $g(x)=−8x+2$

37. $g(x)=3−x$

Responder: a.$g(h^2)=3−h^2$
b.$g(x+2)=1−x$
c.$g(x)+g(2)=4−x$

38. $g(x)=7−5x$

En los siguientes ejercicios, evaluar la función.

39. $f(x)=3x^2−5x$;$f(2)$

Responder: 2

40. $g(x)=4x^2−3x$;$g(3)$

41. $F(x)=2x^2−3x+1$;$F(−1)$

Responder: 6

42. $G(x)=3x^2−5x+2$;$G(−2)$

43. $h(t)=2|t−5|+4$;$f(−4)$

Responder: 22

44. $h(y)=3|y−1|−3$;$h(−4)$

45. $f(x)=x+2x−1$;$f(2)$

Responder: 4

46. $g(x)=x−2x+2$;$g(4)$

En los siguientes ejercicios, resuelve.

47. El número de programas no vistos en el DVR de Sylvia es de 85. Este número crece en 20 programas no vistos por semana. La función$N(t)=85+20t$ representa la relación entre el número de programas no vistos, N, y el tiempo, t, medido en semanas.

a. Determinar la variable independiente y dependiente.

b. Encontrar$N(4)$. Explicar lo que significa este resultado

Responder: a. t IND; N DEP
b.$N(4)=165$ el número de programas no vistos en el DVR de Sylvia a la cuarta semana.

48. Todos los días se descarga un nuevo rompecabezas en la cuenta de Ken. En este momento tiene 43 acertijos en su cuenta. La función$N(t)=43+t$ representa la relación entre el número de rompecabezas, N, y el tiempo, t, medido en días.

a. Determinar la variable independiente y dependiente.

b. Encontrar$N(30)$. Explique qué significa este resultado.

49. El costo diario para la imprenta para imprimir un libro está modelado por la función$C(x)=3.25x+1500$ donde C es el costo total diario y x es el número de libros impresos.

a. Determinar la variable independiente y dependiente.

b. Encontrar$N(0)$. Explique qué significa este resultado.

c. Encontrar$N(1000)$. Explique qué significa este resultado.

Responder: a. x IND; C DEP
b.$N(0)=1500$ el costo diario si no se imprimen libros
c.$N(1000)=4750$ el costo diario de imprimir 1000 libros

50. El costo diario para la empresa manufacturera está modelado por la función$C(x)=7.25x+2500$ donde$C(x)$ está el costo total diario y x es el número de artículos fabricados.

a. Determinar la variable independiente y dependiente.

b. Encontrar$C(0)$. Explique qué significa este resultado.

c. Encontrar$C(1000)$. Explique qué significa este resultado.

Ejercicios de escritura

51. En sus propias palabras, explique la diferencia entre una relación y una función.

52. En sus propias palabras, explique qué se entiende por dominio y rango.

53. ¿Toda relación es una función? ¿Toda función es una relación?

54. ¿Cómo encuentra el valor de una función?

Autocomprobación

a. después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.

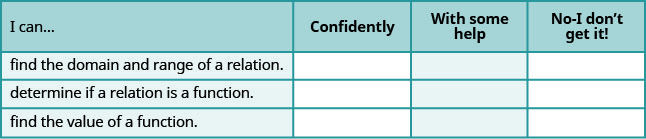
$La figura muestra una tabla con cuatro filas y cuatro columnas. La primera fila es una fila de encabezado y etiqueta cada columna. El encabezado de la primera columna es “puedo...”, el segundo es “con confianza”, el tercero es “con algo de ayuda”, “¡no menos no lo entiendo!”. Debajo de la primera columna están las frases “encontrar el dominio y rango de una relación”, “determinar si una relación es una función”, y “encontrar el valor de una función”. Debajo de la segunda, tercera, cuarta columnas son espacios en blanco donde el alumno puede verificar qué nivel de dominio ha logrado.$

b. después de mirar la lista de verificación, ¿cree que está bien preparado para la siguiente sección? ¿Por qué o por qué no?