4.4E: Ejercicios

Última actualización
Guardar como PDF

Page ID: 112357

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

La práctica hace la perfección

Resolver aplicaciones de mezcla

En los siguientes ejercicios, traducir a un sistema de ecuaciones y resolver.

1. Los boletos para un espectáculo de Broadway cuestan $35 para adultos y $15 para niños. El total de recibos por 1650 boletos a una sola actuación fueron de $47,150. ¿Cuántos boletos de adulto y cuántos niños se vendieron?

2. Los boletos para el espectáculo del Cirque du Soleil cuestan $70 para adultos y $50 para niños. Una actuación vespertina tuvo un total de 300 boletos vendidos y los recibos sumaron 17.200 dólares. ¿Cuántos boletos de adulto y cuántos niños se vendieron?

Responder: 110 boletos para adultos, 190 boletos para niños

3. Los boletos para un tren Amtrak cuestan $10 para niños y $22 para adultos. Josie pagó 1200 dólares por un total de 72 boletos. ¿Cuántos boletos para niños y cuántos boletos para adultos compró Josie?

4. Los boletos para un partido de béisbol de los Minnesota Twins cuestan $69 para asientos de nivel principal y $39 para asientos de Terrace Level. Un grupo de dieciséis amigos acudieron al juego y gastaron un total de 804 dólares para los boletos. ¿Cuántos boletos de Nivel Principal y cuántos boletos de Nivel Terraza compraron?

Responder: 6 buenos asientos, 10 asientos baratos

5. Los boletos para un recital de baile cuestan $15 para adultos y $7 dólares para niños. La compañía de danza vendió 253 boletos y los recibos totales fueron de 2771 dólares. ¿Cuántos boletos para adultos y cuántos boletos infantiles se vendieron?

6. Los boletos para la feria comunitaria cuestan $12 para adultos y $5 dólares para niños. El primer día de la feria se vendieron 312 boletos por un total de 2204 dólares. ¿Cuántos boletos para adultos y cuántos boletos infantiles se vendieron?

Responder: 92 boletos adultos, 220 boletos para niños

7. Brandon tiene una taza de cuartos y diez centavos con un valor total de$$3.80$. El número de trimestres es cuatro menos del doble del número de trimestres. ¿Cuántos cuartos y cuántas monedas de diez centavos tiene Brandon?

8. Sherri ahorra monedas de cinco y diez centavos en un monedero para su hija. El valor total de las monedas en el monedero es$$0.95$. El número de monedas de cinco centavos es dos menos de cinco veces el número de monedas de diez centavos. ¿Cuántas monedas de cinco centavos y cuántas monedas hay en el monedero?

Responder: 13 níqueles, 3 dimes

9. Peter lleva varios días guardando su cambio suelto. Al contar sus cuartos y monedas de cinco centavos, encontró que tenían un valor total$$13.10$. El número de trimestres fue quince más de tres veces el número de monedas de diez centavos. ¿Cuántos cuartos y cuántas monedas de diez centavos tenía Peter?

10. Lucinda tenía un bolsillo lleno de monedas de diez centavos y cuartos con un valor de$$6.20$. El número de monedas de diez centavos es dieciocho más de tres veces el número de trimestres. ¿Cuántas monedas de diez centavos y cuántos cuartos tiene Lucinda?

Responder: 42 dimes, 8 trimestres

11. Un cajero tiene 30 billetes, todos los cuales son billetes de $10 o $20. El valor total del dinero es de $460. ¿Cuántos de cada tipo de factura tiene el cajero?

12. Un cajero tiene 54 billetes, todos los cuales son billetes de $10 o $20. El valor total del dinero es de $910. ¿Cuántos de cada tipo de factura tiene el cajero?

Responder: 17 billetes de $10, 37 billetes de $20

13. Marissa quiere mezclar dulces vendiendo$$1.80$ por libra con dulces que cuestan$$1.20$ por libra para obtener una mezcla que le cuesta$$1.40$ por libra para hacer. Ella quiere hacer 90 libras de la mezcla de dulces. ¿Cuántas libras de cada tipo de caramelo debe usar?

14. ¿Cuántas libras de nueces vendiendo por $6 por libra y pasas vendiendo por $3 por libra debe combinar Kurt para obtener 120 libras de mezcla de trail que le costó $5 por libra?

Responder: 80 libras de nueces y 40 libras de pasas

15. Hannah tiene que hacer veinticinco galones de ponche para una comida. El ponche está hecho de refresco y bebida de frutas. El costo del refresco es$$1.79$ por galón y el costo de la bebida de frutas es$$2.49$ por galón. El presupuesto de Hannah requiere que el ponche cueste$$2.21$ por galón. ¿Cuántos galones de refresco y cuántos galones de bebida de frutas necesita?

16. A José le gustaría hacer doce libras de una mezcla de café a un costo de $6 por libra. Combina Ground Chicoria a $5 la libra con Jamaican Blue Mountain a $9 por libra. ¿Cuánto de cada tipo de café debe usar?

Responder: 9 libras de café de achicoria, 3 libras de café jamaicano Blue Mountain

17. Julia y su esposo son dueños de una cafetería. Experimentaron mezclando un café City Roast Columbian que costó $7.80 por libra con café French Roast Columbian que costó $8.10 por libra para hacer una mezcla de veinte libras. Su mezcla debería costarles $7.92 por libra. ¿Cuánto de cada tipo de café deben comprar?

18. Melody, de doce años, quiere vender bolsas de dulces mezclados en su puesto de limonadas. Ella mezclará M&M's que cuestan $4.89 por bolsa y Reese's Pieces que cuestan $3.79 por bolsa para obtener un total de veinticinco bolsas de dulces mixtos. Melody quiere que las bolsas de dulces mixtos le cuesten $4.23 la bolsa para hacer. ¿Cuántas bolsas de M&M's y cuántas bolsas de Reese's Pieces debería usar?

Responder: 10 bolsas de M&M's, 15 bolsas de Reese's Pieces

19. Jotham necesita 70 litros de una solución al 50% de una solución de alcohol. Tiene una solución de 30% y 80% disponible. ¿Cuántos litros del 30% y cuántos litros de las soluciones al 80% debe mezclar para hacer la solución del 50%?

20. Joy está preparando 15 litros de una solución salina al 25%. Ella solo tiene 40% y 10% de solución en su laboratorio. ¿Cuántos litros del 40% y cuántos litros del 10% debe mezclar para hacer la solución del 25%?

Responder: $7.5$litros de cada solución

21. Un científico necesita 65 litros de una solución alcohólica al 15%. Ella tiene disponible una solución del 25% y una 12%. ¿Cuántos litros del 25% y cuántos litros de las soluciones al 12% debe mezclar para hacer la solución del 15%?

22. Un científico necesita 120 mililitros de una solución ácida al 20% para un experimento. El laboratorio tiene disponible una solución al 25% y una solución al 10%. ¿Cuántos litros del 25% y cuántos litros de las soluciones al 10% debe mezclar el científico para hacer la solución al 20%?

Responder: 80 litros de la solución al 25% y 40 litros de la solución al 10%

23. Una solución anticongelante al 40% se va a mezclar con una solución anticongelante al 70% para obtener 240 litros de una solución al 50%. ¿Cuántos litros del 40% y cuántos litros de las soluciones del 70% se utilizarán?

24. Una solución anticongelante al 90% se va a mezclar con una solución anticongelante al 75% para obtener 360 litros de una solución al 85%. ¿Cuántos litros del 90% y cuántos litros de las soluciones del 75% se utilizarán?

Responder: 240 litros de la solución al 90% y 120 litros de la solución al 75%

Resolver aplicaciones de interés

En los siguientes ejercicios, traducir a un sistema de ecuaciones y resolver.

25. Hattie tenía $3000 para invertir y quiere ganar 10.6% de interés al año. Ella pondrá parte del dinero en una cuenta que gana 12% anual y el resto en una cuenta que gana 10% anual. ¿Cuánto dinero debe poner en cada cuenta?

26. Carol invirtió 2560 dólares en dos cuentas. Una cuenta pagó 8% de interés y la otra pagó 6% de interés. Ella obtuvo 7.25% de interés sobre la inversión total. ¿Cuánto dinero puso en cada cuenta?

Responder: $1600 al 8%, 960 al 6%

27. Sam invirtió 48,000 dólares, algunos con 6% de interés y el resto en 10%. ¿Cuánto invirtió a cada tasa si recibió $4000 en interés en un año?

28. Arnold invirtió 64 mil dólares, algunos con 5.5% de interés y el resto en 9%. ¿Cuánto invirtió a cada tasa si recibió $4500 en interés en un año?

Responder: $28,000 al 9%, $36,000 al 5.5%

29. Después de cuatro años en la universidad, Josie debe 65, 800 dólares en préstamos estudiantiles. La tasa de interés de los préstamos federales es de 4.5% y la tasa de los préstamos bancarios privados es de 2%. El interés total que debe por un año fue$$2878.50$. ¿Cuál es el monto de cada préstamo?

30. Mark quiere invertir 10.000 dólares para pagar la boda de su hija el próximo año. Invertirá parte del dinero en un CD a corto plazo que paga 12% de intereses y el resto en una cuenta de ahorro del mercado monetario que paga 5% de interés. ¿Cuánto debería invertir a cada tasa si quiere ganar $1095 en intereses en un año?

Responder: $8500 CD, $1500 cuenta de ahorros

31. Un fondo fiduciario por valor de $25,000 se invierte en dos carteras diferentes. Este año, se espera que una cartera gane 5.25% de interés y la otra gane 4%. Los planes consisten en que el interés total del fondo sea de $1150 en un año. ¿Cuánto dinero se debe invertir a cada tasa?

32. Un negocio tiene dos préstamos por un total de 85,000 dólares. Un préstamo tiene una tasa del 6% y el otro tiene una tasa de 4.5% Este año, el negocio espera pagar $4,650 en intereses por los dos préstamos. ¿Cuánto cuesta cada préstamo?

Responder: $55,000 en préstamo al 6% y $30,000 en préstamo al 4.5%

Resolver aplicaciones de funciones de costos e ingresos

33. El fabricante de una bebida energética gasta $1.20 para hacer cada bebida y las vende por $2. El fabricante también tiene costos fijos cada mes de $8,000.

ⓐ Encuentra la función de costo C cuando se fabrican x bebidas energéticas.

ⓑ Encuentra la función de ingresos R cuando se venden x bebidas.

ⓓ Encuentra el punto de equilibrio. Interpreta lo que significa el punto de equilibrio.

34. El fabricante de una botella de agua gasta $5 para construir cada botella y las vende por $10. El fabricante también tiene costos fijos cada mes de $6500. ⓐ Encuentre la función de costo C cuando se fabrican x botellas. ⓑ Encuentre la función de ingresos R cuando se venden x botellas. ⓒ Muestre el punto de equilibrio graficando tanto las funciones Ingresos como Costo en el misma cuadrícula. ⓓ Encuentra el punto de equilibrio. Interpreta lo que significa el punto de equilibrio.

Responder

ⓐ$C(x)=5x+6500$

ⓑ$R(x)=10x$

ⓒ

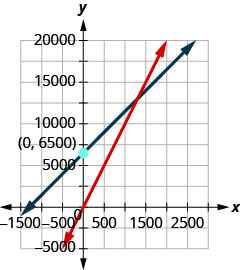
$La figura muestra una gráfica con dos líneas de intersección. Uno de ellos pasa por el origen. El otro cruza el eje y en el punto 6560.$

ⓓ 1,500; cuando se venden 1,500 botellas de agua, el costo y los ingresos equivalen a $15,000

Ejercicios de escritura

35. Toma un puñado de dos tipos de monedas, y escribe un problema similar al Ejemplo relacionando el número total de monedas y su valor total. Configura un sistema de ecuaciones para describir tu situación y luego resolverla.

36. En Ejemplo, se utilizó la eliminación para resolver el sistema de ecuaciones
$\left\{ \begin{array} {l} s+b=40,000 \\ 0.08s+0.03b=0.071(40,000). \end{array} \right. $

¿Podrías haber utilizado la sustitución o eliminación para resolver este sistema? ¿Por qué?

Responder: Las respuestas variarán.

Autocomprobación

ⓐ Después de completar los ejercicios, usa esta lista de verificación para evaluar tu dominio de los objetivos de esta sección.

$Esta tabla tiene 4 columnas, 2 filas y una fila de cabecera. La fila de encabezado etiqueta cada columna puedo, con confianza, con algo de ayuda y no, no la consigo. La primera columna tiene las siguientes declaraciones: resolver aplicaciones de mezcla, resolver aplicaciones de interés. Las columnas restantes están en blanco.$

ⓑ ¿Qué te dice esta lista de verificación sobre tu dominio de esta sección? ¿Qué pasos tomarás para mejorar?