4.6: Resolver sistemas de ecuaciones usando matrices

Última actualización
Guardar como PDF

Page ID: 112332

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

Al final de esta sección, podrás:

Escribir la matriz aumentada para un sistema de ecuaciones
Usar operaciones de fila en una matriz
Resolver sistemas de ecuaciones usando matrices

Antes de comenzar, toma este cuestionario de preparación.

Resolver:$3(x+2)+4=4(2x−1)+9$.
Si te perdiste este problema, revisa [enlace].
Resolver:$0.25p+0.25(x+4)=5.20$.
Si te perdiste este problema, revisa [enlace].
Evaluar cuándo$x=−2$ y$y=3:2x^2−xy+3y^2$.
Si te perdiste este problema, revisa [enlace].

Escribir la Matriz Aumentada para un Sistema de Ecuaciones

Resolver un sistema de ecuaciones puede ser una operación tediosa donde un simple error puede causar estragos en encontrar la solución. Se dispone de un método alternativo que utiliza los procedimientos básicos de eliminación pero con notación más simple. El método implica el uso de una matriz. Una matriz es una matriz rectangular de números dispuestos en filas y columnas.

MATRIX

Una matriz es una matriz rectangular de números dispuestos en filas y columnas.

Una matriz con m filas y n columnas tiene orden$m\times n$. La matriz de abajo a la izquierda tiene 2 filas y 3 columnas y así tiene orden$2\times 3$. Decimos que es una matriz de 2 por 3.

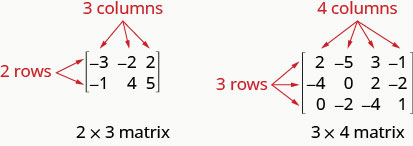
$La figura muestra dos matrices. El de la izquierda tiene los números menos 3, menos 2 y 2 en la primera fila y los números menos 1, 4 y 5 en la segunda fila. Las filas y columnas están encerradas entre corchetes. Así, tiene 2 filas y 3 columnas. Se etiqueta 2 cruz 3 o 2 por 3 matriz. La matriz de la derecha es similar pero con 3 filas y 4 columnas. Está etiquetada con matriz 3 por 4.$

Cada número en la matriz se llama un elemento o entrada en la matriz.

Utilizaremos una matriz para representar un sistema de ecuaciones lineales. Escribimos cada ecuación en forma estándar y los coeficientes de las variables y la constante de cada ecuación se convierte en una fila en la matriz. Cada columna sería entonces los coeficientes de una de las variables en el sistema o las constantes. Una línea vertical reemplaza los signos iguales. Llamamos a la matriz resultante la matriz aumentada para el sistema de ecuaciones.

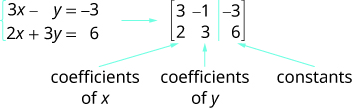
$Las ecuaciones son 3x más y es igual a menos 3 y 2x más 3y es igual a 6. Se muestra una matriz de 2 por 3. La primera fila es 3, 1, menos 3. La segunda fila es 2, 3, 6. La primera columna está etiquetada como coeficientes de x. La segunda columna está etiquetada como coeficientes de y y la tercera está etiquetada como constantes.$

Observe que la primera columna está compuesta por todos los coeficientes de x, la segunda columna son los todos los coeficientes de y, y la tercera columna son todas las constantes.

Ejemplo$\PageIndex{1}$

ⓐ$\left\{ \begin{array} {l} 5x−3y=−1 \\ y=2x−2 \end{array} \right. $ ⓑ$ \left\{ \begin{array} {l} 6x−5y+2z=3 \\ 2x+y−4z=5 \\ 3x−3y+z=−1 \end{array} \right. $

Contestar

ⓐ La segunda ecuación no está en forma estándar. Reescribimos la segunda ecuación en forma estándar.

\[\begin{aligned} y=2x−2 \\ −2x+y=−2 \end{aligned} \nonumber\]

Sustituimos la segunda ecuación por su forma estándar. En la matriz aumentada, la primera ecuación nos da la primera fila y la segunda ecuación nos da la segunda fila. La línea vertical sustituye a los signos iguales.

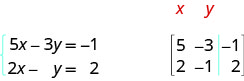
ⓑ Las tres ecuaciones están en forma estándar. En la matriz aumentada la primera ecuación nos da la primera fila, la segunda ecuación nos da la segunda fila, y la tercera ecuación nos da la tercera fila. La línea vertical sustituye a los signos iguales.

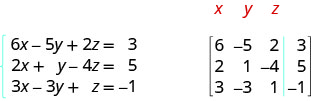
$Las ecuaciones son 6x menos 5y más 2z es igual a 3, 2x más y menos 4z es igual a 5 y 3x menos 3y más z es igual a menos 1. Se muestra una matriz de 4 por 3 cuya primera fila es 6, menos 5, 2, 3. Su segunda fila es 2, 1, menos 4, 5. Su tercera fila es 3, menos 3, 1 y menos 1. Sus tres primeras columnas están etiquetadas x, y y z respectivamente.$

Ejemplo$\PageIndex{2}$

Escribe cada sistema de ecuaciones lineales como una matriz aumentada:

ⓐ$\left\{ \begin{array} {l} 3x+8y=−3 \\ 2x=−5y−3 \end{array} \right. $ ⓑ$\left\{ \begin{array} {l} 2x−5y+3z=8 \\ 3x−y+4z=7 \\ x+3y+2z=−3 \end{array} \right. $

Contestar

ⓐ$\left[ \begin{matrix} 3 &8 &-3 \\ 2 &5 &−3 \end{matrix} \right] $

ⓑ$\left[ \begin{matrix} 2 &3 &1 &−5 \\ −1 &3 &3 &4 \\ 2 &8 &7 &−3 \end{matrix} \right] $

Ejemplo$\PageIndex{3}$

Escribe cada sistema de ecuaciones lineales como una matriz aumentada:

ⓐ$\left\{ \begin{array} {l} 11x=−9y−5 \\ 7x+5y=−1 \end{array} \right. $ ⓑ$\left\{ \begin{array} {l} 5x−3y+2z=−5 \\ 2x−y−z=4 \\ 3x−2y+2z=−7 \end{array} \right. $

Contestar: ⓐ$\left[ \begin{matrix} 11 &9 &−5 \\ 7 &5 &−1 \end{matrix} \right] $
ⓑ$\left[ \begin{matrix} 5 &−3 &2 &−5 \\ 2 &−1 &−1 &4 \\ 3 &−2 &2 &−7 \end{matrix} \right] $

Es importante ya que resolvemos sistemas de ecuaciones utilizando matrices para poder ir y venir entre el sistema y la matriz. El siguiente ejemplo nos pide tomar la información en la matriz y escribir el sistema de ecuaciones.

Ejemplo$\PageIndex{4}$

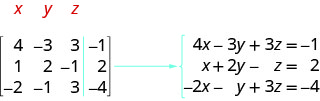
Escribe el sistema de ecuaciones que corresponde a la matriz aumentada:

$\left[ \begin{array} {ccc|c} 4 &−3 &3 &−1 \\ 1 &2 &−1 &2 \\ −2 &−1 &3 &−4 \end{array} \right] $.

Contestar

Recordamos que cada fila corresponde a una ecuación y que cada entrada es un coeficiente de una variable o la constante. La línea vertical reemplaza al signo igual. Dado que esta matriz es una$4\times 3$, sabemos que se traducirá en un sistema de tres ecuaciones con tres variables.

$Se muestra una matriz de 3 por 4. Su primera fila es 4, menos 3, 3, menos 1. Su segunda fila es 1, 2, menos 1, 2. Su tercera fila es menos 2, menos 1, 3, menos 4. Las tres ecuaciones son 4x menos 3y más 3z es igual a menos 1, x más 2y menos z es igual a 2 y menos 2x menos y más 3z es igual a menos 4.$

Ejemplo$\PageIndex{5}$

Escribe el sistema de ecuaciones que corresponde a la matriz aumentada:$\left[ \begin{matrix} 1 &−1 &2 &3 \\ 2 &1 &−2 &1 \\ 4 &−1 &2 &0 \end{matrix} \right] $.

Contestar: $\left\{ \begin{array} {l} x−y+2z=3 \\ 2x+y−2z=1 \\ 4x−y+2z=0 \end{array} \right.$

Ejemplo$\PageIndex{6}$

Escribe el sistema de ecuaciones que corresponde a la matriz aumentada:$\left[ \begin{matrix} 1 &1 &1 &4 \\ 2 &3 &−1 &8 \\ 1 &1 &−1 &3 \end{matrix} \right] $.

Contestar: $\left\{ \begin{array} {l} x+y+z=4 \\ 2x+3y−z=8 \\ x+y−z=3 \end{array} \right.$

Usar operaciones de fila en una matriz

Una vez que un sistema de ecuaciones está en su forma de matriz aumentada, realizaremos operaciones en las filas que nos llevarán a la solución.

Para resolver por eliminación, no importa en qué orden coloquemos las ecuaciones en el sistema. De igual manera, en la matriz podemos intercambiar las filas.

Cuando resolvemos por eliminación, muchas veces multiplicamos una de las ecuaciones por una constante. Dado que cada fila representa una ecuación, y podemos multiplicar cada lado de una ecuación por una constante, de manera similar podemos multiplicar cada entrada en una fila por cualquier número real excepto 0.

En la eliminación, a menudo agregamos un múltiplo de una fila a otra fila. En la matriz podemos sustituir una fila con su suma por un múltiplo de otra fila.

Estas acciones se denominan operaciones de fila y nos ayudarán a usar la matriz para resolver un sistema de ecuaciones.

OPERACIONES EN FILA

En una matriz, se pueden realizar las siguientes operaciones en cualquier fila y la matriz resultante será equivalente a la matriz original.

Intercambia dos filas cualesquiera.
Multiplica una fila por cualquier número real excepto 0.
Agrega un múltiplo distinto de cero de una fila a otra fila.

Realizar estas operaciones es fácil de hacer pero toda la aritmética puede resultar en un error. Si utilizamos un sistema para registrar la operación de fila en cada paso, es mucho más fácil volver atrás y revisar nuestro trabajo.

Utilizamos letras mayúsculas con subíndices para representar cada fila. A continuación mostramos la operación a la izquierda de la nueva matriz. Para mostrar el intercambio de una fila:

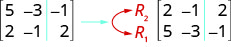
$Se muestra una matriz de 2 por 3. Su primera fila, etiquetada como R2 es 2, menos 1, 2. Su segunda fila, etiquetada con R1 es 5, menos 3, menos 1.$

Para multiplicar la fila 2 por$−3$:

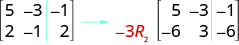
$Se muestra una matriz de 2 por 3. Su primera fila es 5, menos 3, menos 1. Su segunda fila es 2, menos 1, 2. Una flecha apunta desde esta matriz a otra de la derecha. La primera fila de la nueva matriz es la misma. La segunda fila va precedida por menos 3 R2. Es menos 6, 3, menos 6.$

Para multiplicar la fila 2 por$−3$ y agregarla a la fila 1:

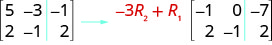
$Se muestra una matriz de 2 por 3. Su primera fila es 5, menos 3, menos 1. Su segunda fila es 2, menos 1, 2. Una flecha apunta desde esta matriz a otra de la derecha. La primera fila de la nueva matriz está precedida por menos 3 R2 más R1. Es menos 1, 0, menos 7. La segunda fila es 2, menos 1, 2.$

Ejemplo$\PageIndex{7}$

Realizar las operaciones indicadas en la matriz aumentada:

ⓐ Intercambia las filas 2 y 3.

ⓑ Multiplica la fila 2 por 5.

$ \left[ \begin{array} {ccc|c} 6 &−5 &2 &3 \\ 2 &1 &−4 &5 \\ 3 &−3 &1 &−1 \end{array} \right] $

Contestar

ⓐ Intercambiamos las filas 2 y 3.

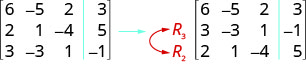
$Se muestran dos matrices de 3 por 4. En la de la izquierda, la primera fila es 6, menos 5, 2, 3. La segunda fila es 2, 1, menos 4, 5. La tercera fila es 3, menos 3, 1, menos 1. La segunda matriz es similar excepto que se intercambian las filas 2 y 3.$

ⓑ Multiplicamos la fila 2 por 5.

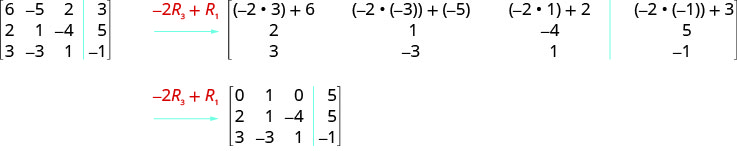
$En la matriz 3 por 4, la primera fila es 6, menos 5, 2, 3. La segunda fila es 2, 1, menos 4, 5. La tercera fila es 3, menos 3, 1, menos 1. Al realizar la operación menos 2 R3 más R1 en la primera fila, la primera fila se convierte en 6 más menos 2 veces 3, menos 5 más menos 2 veces menos 3, 2 más menos 2 veces 1 y 3 más menos 2 veces menos 1. Esto se convierte en 0, 1, 0, 5. Las 2 filas restantes de la nueva matriz son las mismas.$

Ejemplo$\PageIndex{8}$

Realizar las operaciones indicadas en la matriz aumentada:

ⓐ Intercambia las filas 1 y 3.

ⓑ Multiplica la fila 3 por 3.

$ \left[ \begin{array} {ccc|c} 5 &−2 &-2 &-2 \\ 4 &-1 &−4 &4 \\ -2 &3 &0 &−1 \end{array} \right] $

Contestar

ⓐ$ \left[ \begin{matrix} −2 &3 &0 &−2 \\ 4 &−1 &−4 &4 \\ 5 &−2 &−2 &−2 \end{matrix} \right] $

ⓑ$ \left[ \begin{matrix} −2 &3 &0 &−2 \\ 4 &−1 &−4 &4 \\ 15 &−6 &−6 &−6 \end{matrix} \right] $

ⓒ$ \left[ \begin{matrix} -2 &3 &0 &2 & \\ 3 &4 &-13 &-16 &-8 \\ 15 &-6 &-6 &-6 & \end{matrix} \right] $

Ejemplo$\PageIndex{9}$

Realizar las operaciones indicadas en la matriz aumentada:

ⓐ Intercambia las filas 1 y 2,

ⓑ Multiplicar fila 1 por 2,

$ \left[ \begin{array} {ccc|c} 2 &−3 &−2 &−4 \\ 4 &1 &−3 &2 \\ 5 &0 &4 &−1 \end{array} \right] $

Contestar: ⓐ$ \left[ \begin{matrix} 4 &1 &−3 &2 \\ 2 &−3 &−2 &−4 \\ 5 &0 &4 &−1 \end{matrix} \right] $
ⓑ$ \left[ \begin{matrix} 8 &2 &−6 &4 \\ 2 &−3 &−2 &−4 \\ 5 &0 &4 &−1 \end{matrix} \right] $
ⓒ$ \left[ \begin{matrix} 14 &−7 &−12 &−8 \\ 2 &−3 &−2 &−4 \\ 5 &0 &4 &−1 \end{matrix} \right] $

Ahora que hemos practicado las operaciones de fila, veremos una matriz aumentada y averiguaremos qué operación usaremos para alcanzar una meta. Esto es exactamente lo que hicimos cuando hicimos la eliminación. Decidimos por qué número multiplicar una fila para que se eliminara una variable cuando sumáramos las filas juntas.

Dado este sistema, ¿qué harías para eliminar x?

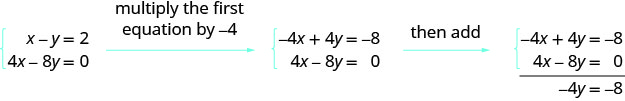
$Las dos ecuaciones son x menos y es igual a 2 y 4x menos 8y es igual a 0. Multiplicando el primero por menos 4, obtenemos menos 4x más 4y es igual a menos 8. Añadiendo esto a la segunda ecuación obtenemos menos 4y es igual a menos 8.$

Este siguiente ejemplo esencialmente hace lo mismo, pero a la matriz.

Ejemplo$\PageIndex{10}$

Realice la operación de fila necesaria que hará que la primera entrada en la fila 2 sea cero en la matriz aumentada:$ \left[ \begin{array} {cc|c} 1 &−1 &2 \\ 4 &−8 &0 \end{array} \right] $

Contestar

Para hacer el 4 a 0, podríamos multiplicar la fila 1 por$−4$ y luego agregarla a la fila 2.

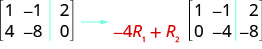
$La matriz 2 por 3 es 1, menos 1, 2 y 4, menos 8, 0. Al realizar la operación menos 4R1 más R2 en la fila 2, la segunda fila de la nueva matriz se convierte en 0, menos 4, menos 8. La primera fila sigue siendo la misma.$

Ejemplo$\PageIndex{11}$

Realice la operación de fila necesaria que hará que la primera entrada en la fila 2 sea cero en la matriz aumentada:$ \left[ \begin{array} {cc|c} 1 &−1 &2 \\ 3 &−6 &2 \end{array} \right] $

Contestar: $ \left[ \begin{matrix} 1 &−1 &2 \\ 0 &−3 &−4 \end{matrix} \right] $

Ejemplo$\PageIndex{12}$

Realice la operación de fila necesaria que hará que la primera entrada en la fila 2 sea cero en la matriz aumentada:$ \left[ \begin{array} {cc|c} 1 &−1 &3 \\ -2 &−3 &2 \end{array} \right] $

Contestar: $ \left[ \begin{matrix} 1 &−1 &3 \\ 0 &−5 &8 \end{matrix} \right] $

Resolver Sistemas de Ecuaciones Usando Matrices

Para resolver un sistema de ecuaciones usando matrices, transformamos la matriz aumentada en una matriz en forma de fila-escalón usando operaciones de fila. Para un sistema consistente e independiente de ecuaciones, su matriz aumentada está en forma de fila-escalón cuando a la izquierda de la línea vertical, cada entrada en la diagonal es un 1 y todas las entradas por debajo de la diagonal son ceros.

FORMULARIO DE FILA

Para un sistema consistente e independiente de ecuaciones, su matriz aumentada está en forma de fila-escalón cuando a la izquierda de la línea vertical, cada entrada en la diagonal es un 1 y todas las entradas por debajo de la diagonal son ceros.

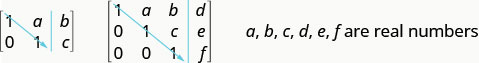
$A la izquierda se muestra una matriz de 2 por 3. Su primera fila es 1, a, b. Su segunda fila es 0, 1, c. Una flecha apunta diagonalmente hacia abajo y hacia la derecha, superponiendo ambos 1s en la matriz. A la derecha se muestra una matriz de 3 por 4. Su primera fila es 1, a, b, d. Su segunda fila es 0, 1, c, e. Su tercera fila es 0, 0, 1, f. Una flecha apunta diagonalmente hacia abajo y hacia la derecha, superponiendo todos los 1s en la matriz. a, b, c, d, e, f son números reales.$

Una vez que obtenemos la matriz aumentada en forma de fila-escalón, podemos escribir el sistema equivalente de ecuaciones y leer el valor de al menos una variable. Luego sustituimos este valor en otra ecuación para continuar resolviendo por las otras variables. Este proceso se ilustra en el siguiente ejemplo.

Cómo Resolver un Sistema de Ecuaciones Usando una Matriz

Resuelve el sistema de ecuaciones usando una matriz:$\left\{ \begin{array} {l} 3x+4y=5 \\ x+2y=1 \end{array} \right. $

Contestar: $Las ecuaciones son 3x más 4y es igual a 5 y x más 2y es igual a 1. Paso 1. Escribir la matriz aumentada para el sistema de ecuaciones. Obtenemos una matriz de 2 por 3 con primera fila 3, 4, 5 y segunda fila 1, 2, 1.$ $Paso 2. El uso de operaciones de fila consigue que la entrada en la fila 1, columna 1 sea 1. Intercambia las filas R1 y R2.$ $Paso 3. Usando operaciones de fila, obtenga ceros en la columna 1 debajo del 1. Multiplica la fila 1 por menos 3 y agrégala a la fila 2. La fila 2 se convierte en 0, menos 2, 2.$ $Paso 4. Usando operaciones de fila, obtenga que la entrada en la fila 2, columna 2 sea 1. Multiplica la fila 2 por menos la mitad. La fila 2 se convierte en 0, 1, menos 1.$ $Paso 5. Continuar el proceso hasta que la matriz esté en forma de fila-escalón. La matriz se encuentra ahora en forma de fila-escalón.$ $Paso 6. Escribir el sistema de ecuaciones correspondiente. Obtenemos x más 2y es igual a 1 e y es igual a menos 1.$ $Paso 7. Utilice la sustitución para encontrar las variables restantes. Sustituir y es igual a 1 negativo en x más 2y es igual a 1. X más 2 veces negativo 1 es igual a 1. X menos 2 es igual a 1. Obtenemos x igual a 3.$ $Paso 8. Escribe la solución como un par ordenado o triple. El par ordenado es (3, negativo 1).$ $Paso 9. Comprobar que la solución haga verdaderas las ecuaciones originales.$

Ejemplo$\PageIndex{14}$

Resuelve el sistema de ecuaciones usando una matriz:$\left\{ \begin{array} {l} 2x+y=7 \\ x−2y=6 \end{array} \right. $

Contestar: La solución es$(4,−1)$.

Ejemplo$\PageIndex{15}$

Resuelve el sistema de ecuaciones usando una matriz:$\left\{ \begin{array} {l} 2x+y=−4 \\ x−y=−2 \end{array} \right. $

Contestar: La solución es$(−2,0)$.

Aquí se resumen los pasos.

RESUELVE UN SISTEMA DE ECUACIONES UTILIZANDO

Escribir la matriz aumentada para el sistema de ecuaciones.
El uso de operaciones de fila consigue que la entrada en la fila 1, columna 1 sea 1.
Usando operaciones de fila, obtenga ceros en la columna 1 debajo del 1.
Usando operaciones de fila, obtenga que la entrada en la fila 2, columna 2 sea 1.
Continuar el proceso hasta que la matriz esté en forma de fila-escalón.
Escribir el sistema de ecuaciones correspondiente.
Utilice la sustitución para encontrar las variables restantes.
Escribe la solución como un par ordenado o triple.
Comprobar que la solución haga verdaderas las ecuaciones originales.

Aquí hay un visual para mostrar el orden para obtener los 1's y 0's en la posición adecuada para la forma fila-escalón.

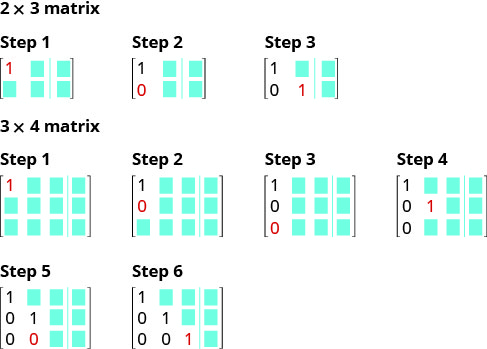
$La figura muestra 3 pasos para una matriz de 2 por 3 y 6 pasos para una matriz de 3 por 4. Para el primero, el paso 1 es obtener un 1 en la fila 1 columna 1. Paso a es obtener un 0 es fila 2 columna 1. El paso 3 es obtener un 1 en la fila 2 columna 2. Para una matriz de 3 por 4, el paso 1 es obtener un 1 en la fila 1 columna 1. El paso 2 es obtener un 0 en la fila 2 columna 1. El paso 3 es obtener un 0 en la fila 3 columna 1. El paso 4 es obtener un 1 en la fila 2 columna 2. El paso 5 es obtener un 0 en la fila 3 columna 2. El paso 6 es obtener un 1 en la fila 3 columna 3.$

Utilizamos el mismo procedimiento cuando el sistema de ecuaciones tiene tres ecuaciones.

Ejemplo$\PageIndex{16}$

Resuelve el sistema de ecuaciones usando una matriz:$\left\{ \begin{array} {l} 3x+8y+2z=−5 \\ 2x+5y−3z=0 \\ x+2y−2z=−1 \end{array} \right. $

Contestar

	$.$
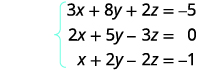
Escribe la matriz aumentada para las ecuaciones.	$.$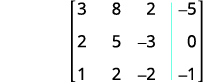
Intercambia las filas 1 y 3 para que la entrada en la fila 1, la columna 1 sea 1.	$.$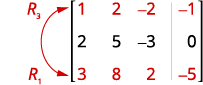
Usando operaciones de fila, obtenga ceros en la columna 1 debajo del 1.	$.$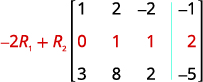
	$.$
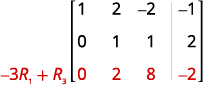
La entrada en la fila 2, columna 2 es ahora 1.
Continuar el proceso hasta que la matriz esté en forma de fila-escalón.	$.$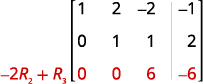
	$.$
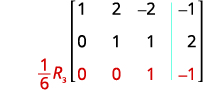
La matriz se encuentra ahora en forma de fila-escalón.	$.$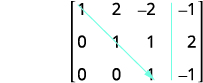
Escribir el sistema de ecuaciones correspondiente.	$.$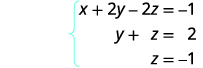
Utilice la sustitución para encontrar las variables restantes.	$.$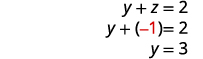
	$.$ $.$
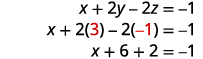
Escribe la solución como un par ordenado o triple.	$.$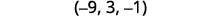
Comprobar que la solución haga verdaderas las ecuaciones originales.	Te dejamos el cheque.

Ejemplo$\PageIndex{17}$

Resuelve el sistema de ecuaciones usando una matriz:$\left\{ \begin{array} {l} 2x−5y+3z=8 \\ 3x−y+4z=7 \\ x+3y+2z=−3 \end{array} \right. $

Contestar: $(6,−1,−3)$

Ejemplo$\PageIndex{18}$

Resuelve el sistema de ecuaciones usando una matriz:$\left\{ \begin{array} {l} −3x+y+z=−4 \\ −x+2y−2z=1 \\ 2x−y−z=−1 \end{array} \right. $

Contestar: $(5,7,4)$

Hasta ahora nuestro trabajo con matrices solo ha sido con sistemas que son consistentes e independientes, lo que significa que tienen exactamente una solución. Veamos ahora qué sucede cuando usamos una matriz para un sistema dependiente o inconsistente.

Ejemplo$\PageIndex{19}$

Resuelve el sistema de ecuaciones usando una matriz:$\left\{ \begin{array} {l} x+y+3z=0 \\ x+3y+5z=0 \\ 2x+4z=1 \end{array} \right. $

Contestar

	$.$
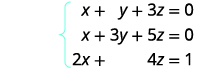
Escribe la matriz aumentada para las ecuaciones.	$.$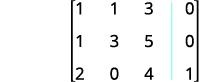
La entrada en la fila 1, columna 1 es 1.
Usando operaciones de fila, obtenga ceros en la columna 1 debajo del 1.	$.$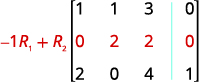
	$.$
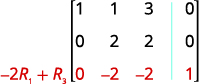
Continuar el proceso hasta que la matriz esté en forma de fila-escalón.	$.$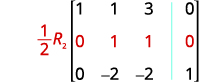
Multiplica la fila 2 por 2 y agrégala a la fila 3.	$.$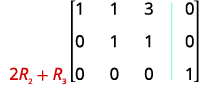
En este punto, tenemos todos los ceros a la izquierda de la fila 3.
Escribir el sistema de ecuaciones correspondiente.	$.$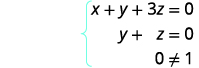
Ya$0 \neq 1 $ que tenemos una declaración falsa. Así como cuando resolvimos un sistema usando otros métodos, esto nos dice que tenemos un sistema inconsistente. No hay solución.

Ejemplo$\PageIndex{20}$

Resuelve el sistema de ecuaciones usando una matriz:$\left\{ \begin{array} {l} x−2y+2z=1 \\ −2x+y−z=2 \\ x−y+z=5 \end{array} \right. $

Contestar: no hay solución

Ejemplo$\PageIndex{21}$

Resuelve el sistema de ecuaciones usando una matriz:$\left\{ \begin{array} {l} 3x+4y−3z=−2 \\ −2x+3y−z=−1 \\ 2x+y−2z=6 \end{array} \right. $

Contestar: no hay solución

El último sistema era inconsistente y por lo tanto no tenía soluciones. El siguiente ejemplo es dependiente y tiene infinitamente muchas soluciones.

Ejemplo$\PageIndex{22}$

Resuelve el sistema de ecuaciones usando una matriz:$\left\{ \begin{array} {l} x−2y+3z=1 \\ x+y−3z=7 \\ 3x−4y+5z=7 \end{array} \right. $

Contestar

	$.$
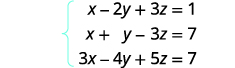
Escribe la matriz aumentada para las ecuaciones.	$.$
La entrada en la fila 1, columna 1 es 1.
Usando operaciones de fila, obtenga ceros en la columna 1 debajo del 1.	$.$
	$.$
Continuar el proceso hasta que la matriz esté en forma de fila-escalón.	$.$
Multiplica la fila 2 por$−2$ y agrégala a la fila 3.	$.$
En este punto, tenemos todos los ceros en la fila inferior.
Escribir el sistema de ecuaciones correspondiente.	$.$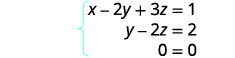
Ya$0=0$ que tenemos una declaración verdadera. Así como cuando resolvimos por sustitución, esto nos dice que tenemos un sistema dependiente. Hay infinitamente muchas soluciones.
Resolver para y en términos de z en la segunda ecuación.	$.$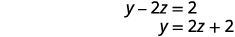
Resuelve la primera ecuación para x en términos de z.	$.$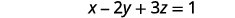
Sustituto$y=2z+2$.	$.$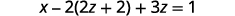
Simplificar.	$.$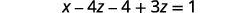
Simplificar.	$.$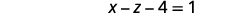
Simplificar.	$.$
El sistema tiene infinitamente muchas soluciones$(x,y,z)$, donde$x=z+5;\space y=2z+2;\space z$ está cualquier número real.

Ejemplo$\PageIndex{23}$

Resuelve el sistema de ecuaciones usando una matriz:$\left\{ \begin{array} {l} x+y−z=0 \\ 2x+4y−2z=6 \\ 3x+6y−3z=9 \end{array} \right. $

Contestar: infinitamente muchas soluciones$(x,y,z)$, donde$x=z−3;\space y=3;\space z$ está cualquier número real.

Ejemplo$\PageIndex{24}$

Resuelve el sistema de ecuaciones usando una matriz:$\left\{ \begin{array} {l} x−y−z=1 \\ −x+2y−3z=−4 \\ 3x−2y−7z=0 \end{array} \right. $

Contestar: infinitamente muchas soluciones$(x,y,z)$, donde$x=5z−2;\space y=4z−3;\space z$ está cualquier número real.

Acceda a este recurso en línea para obtener instrucción y práctica adicionales con Eliminación Gaussiana.

Eliminación Gaussiana

Conceptos clave

Matriz: Una matriz es una matriz rectangular de números dispuestos en filas y columnas. Una matriz con m filas y n columnas tiene orden$m\times n$. La matriz de abajo a la izquierda tiene 2 filas y 3 columnas y así tiene orden$2\times 3$. Decimos que es una matriz de 2 por 3.
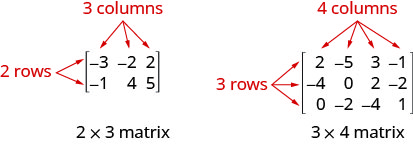
$La figura muestra dos matrices. El de la izquierda tiene los números menos 3, menos 2 y 2 en la primera fila y los números menos 1, 4 y 5 en la segunda fila. Las filas y columnas están encerradas entre corchetes. Así, tiene 2 filas y 3 columnas. Se etiqueta 2 cruz 3 o 2 por 3 matriz. La matriz de la derecha es similar pero con 3 filas y 4 columnas. Está etiquetada con matriz 3 por 4.$
Cada número en la matriz se llama un elemento o entrada en la matriz.
Operaciones de Fila: En una matriz, se pueden realizar las siguientes operaciones en cualquier fila y la matriz resultante será equivalente a la matriz original.
- Intercambia cualquiera de dos filas
- Multiplica una fila por cualquier número real excepto 0
- Agregar un múltiplo distinto de cero de una fila a otra fila
Forma Fila-Escalón: Para un sistema consistente e independiente de ecuaciones, su matriz aumentada está en forma de fila-escalón cuando a la izquierda de la línea vertical, cada entrada en la diagonal es un 1 y todas las entradas por debajo de la diagonal son ceros.
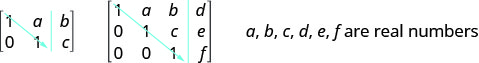
$La figura muestra dos matrices. El de la izquierda tiene los números menos 3, menos 2 y 2 en la primera fila y los números menos 1, 4 y 5 en la segunda fila. Las filas y columnas están encerradas entre corchetes. Así, tiene 2 filas y 3 columnas. Se etiqueta 2 cruz 3 o 2 por 3 matriz. La matriz de la derecha es similar pero con 3 filas y 4 columnas. Está etiquetada con matriz 3 por 4.$
Cómo resolver un sistema de ecuaciones usando matrices.
1. Escribir la matriz aumentada para el sistema de ecuaciones.
2. El uso de operaciones de fila consigue que la entrada en la fila 1, columna 1 sea 1.
3. Usando operaciones de fila, obtenga ceros en la columna 1 debajo del 1.
4. Usando operaciones de fila, obtenga que la entrada en la fila 2, columna 2 sea 1.
5. Continuar el proceso hasta que la matriz esté en forma de fila-escalón.
6. Escribir el sistema de ecuaciones correspondiente.
7. Utilice la sustitución para encontrar las variables restantes.
8. Escribe la solución como un par ordenado o triple.
9. Comprobar que la solución haga verdaderas las ecuaciones originales.

Glosario

matriz: Una matriz es una matriz rectangular de números dispuestos en filas y columnas.

forma fila-escalón: Una matriz está en forma de fila-escalón cuando a la izquierda de la línea vertical, cada entrada en la diagonal es un 1 y todas las entradas por debajo de la diagonal son ceros.

Search

MATRIX

Ejemplo\(\PageIndex{1}\)

Ejemplo\(\PageIndex{2}\)

Ejemplo\(\PageIndex{3}\)

Ejemplo\(\PageIndex{4}\)

Ejemplo\(\PageIndex{5}\)

Ejemplo\(\PageIndex{6}\)

OPERACIONES EN FILA

Ejemplo\(\PageIndex{7}\)

Ejemplo\(\PageIndex{8}\)

Ejemplo\(\PageIndex{9}\)

Ejemplo\(\PageIndex{10}\)

Ejemplo\(\PageIndex{11}\)

Ejemplo\(\PageIndex{12}\)

FORMULARIO DE FILA

Cómo Resolver un Sistema de Ecuaciones Usando una Matriz

Ejemplo\(\PageIndex{14}\)

Ejemplo\(\PageIndex{15}\)

RESUELVE UN SISTEMA DE ECUACIONES UTILIZANDO

Ejemplo\(\PageIndex{16}\)

Ejemplo\(\PageIndex{17}\)

Ejemplo\(\PageIndex{18}\)

Ejemplo\(\PageIndex{19}\)

Ejemplo\(\PageIndex{20}\)

Ejemplo\(\PageIndex{21}\)

Ejemplo\(\PageIndex{22}\)

Ejemplo\(\PageIndex{23}\)

Ejemplo\(\PageIndex{24}\)