4.7: Resolver sistemas de ecuaciones usando determinantes
- Page ID
- 112363
Al final de esta sección, podrás:
- Evaluar el determinante de una matriz 2×2
- Evaluar el determinante de una matriz 3×3
- Usa la regla de Cramer para resolver sistemas de ecuaciones
- Resolver aplicaciones usando determinantes
Antes de comenzar, toma este cuestionario de preparación.
En esta sección aprenderemos de otro método para resolver sistemas de ecuaciones lineales llamado regla de Cramer. Antes de que podamos comenzar a usar la regla, necesitamos aprender algunas definiciones y notación nuevas.
Evaluar el Determinante de una\(2×2\) Matriz
Si una matriz tiene el mismo número de filas y columnas, la llamamos matriz cuadrada. Cada matriz cuadrada tiene un número real asociado a ella llamado su determinante. Para encontrar el determinante de la matriz cuadrada\(\left[ \begin{matrix} a &b \\ c&d \end{matrix} \right] \), primero la escribimos como\(\left| \begin{matrix} a &b \\ c&d \end{matrix} \right| \). Para obtener el valor de número real del determinado restamos los productos de las diagonales, como se muestra.
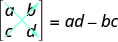
El determinante de cualquier matriz cuadrada\(\left[ \begin{matrix} a &b \\ c&d \end{matrix} \right] \), donde a, b, c y d son números reales, es
\[\left| \begin{matrix} a &b \\ c&d \end{matrix} \right| =ad−bc \nonumber \]
Evaluar el determinado de ⓐ\(\left[ \begin{matrix} 4 &-2 \\ 3&-1 \end{matrix} \right] \) ⓑ\(\left[ \begin{matrix} -3 &-4 \\ -2&0 \end{matrix} \right] \).
- Contestar
-
ⓐ

Escribe el determinante. 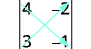
Restar los productos de las diagonales. 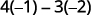
Simplificar. 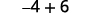
Simplificar. 
ⓑ
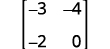
Escribe el determinante. 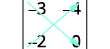
Restar los productos de las diagonales. 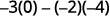
Simplificar. 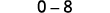
Simplificar. 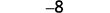
Evaluar el determinado de ⓐ\(\left[ \begin{matrix} 5&−3\\2&−4 \end{matrix} \right] \) ⓑ\(\left[ \begin{matrix} −4&−6\\0&7 \end{matrix} \right] \).
- Contestar
-
ⓐ\(−14\); ⓑ\(−28\)
Evaluar el determinado de ⓐ\(\left[ \begin{matrix} −1&3\\−2&4 \end{matrix} \right] \) ⓑ\(\left[ \begin{matrix} −7&−3\\−5&0 \end{matrix} \right] \).
- Contestar
-
ⓐ 2 ⓑ\(−15\)
Evaluar el Determinante de una\(3×3\) Matriz
Para evaluar el determinante de una\(3×3\) matriz, tenemos que ser capaces de evaluar el menor de una entrada en el determinante. El menor de una entrada es el\(2×2\) determinante encontrado al eliminar la fila y columna en el\(3×3\) determinante que contiene la entrada.
El menor de una entrada en un\(3×3\) determinante es el\(2×2\) determinante encontrado al eliminar la fila y columna en el\(3×3\) determinante que contiene la entrada.
Para encontrar al menor de entrada\(a_1\), eliminamos la fila y columna que lo contienen. Entonces eliminamos la primera fila y la primera columna. Entonces escribimos el\(2×2\) determinante que queda.

Para encontrar al menor de entrada\(b_2\), eliminamos la fila y columna que lo contienen. Entonces eliminamos la\(2^{nd}\) fila y\(2^{nd}\) columna. Entonces escribimos el\(2×2\) determinante que queda.

Para el determinante\(\left| \begin{matrix} 4&−2&3\\1&0&−3\\−2&−4&2 \end{matrix} \right|\), encontrar y luego evaluar al menor de ⓐ\(a_1\) ⓑ\(b_3\) ⓒ\(c_2\).
- Contestar
-
ⓐ
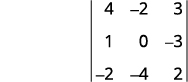
Elimina la fila y columna que contiene\(a_1\). 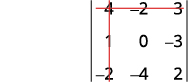
Escribe el\(2×2\) determinante que queda. 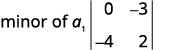
Evaluar. 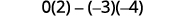
Simplificar. 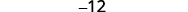
ⓑ
Elimina la fila y columna que contiene\(b_3\). 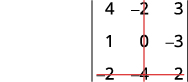
Escribe el\(2×2\) determinante que queda. 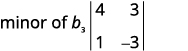
Evaluar. 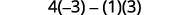
Simplificar. 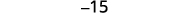
ⓒ
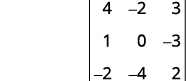
Elimina la fila y columna que contiene\(c_2\). 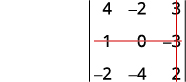
Escribe el\(2×2\) determinante que queda. 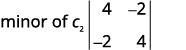
Evaluar. 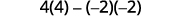
Simplificar. 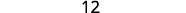
Para el determinante\(\left| \begin{matrix} 1&−1&4\\0&2&−1\\−2&−3&3 \end{matrix} \right|\), encontrar y luego evaluar al menor de ⓐ\(a_1\) ⓑ\(b_2\) ⓒ\(c_3\).
- Contestar
-
ⓐ 3 ⓑ 11 ⓒ 2
Para el determinante\(\left| \begin{matrix} −2&−1&0\\3&0&−1\\−1&−2&3 \end{matrix} \right|\), encontrar y luego evaluar al menor de ⓐ\(a_2\) ⓑ\(b_3\) ⓒ\(c_2\).
- Contestar
-
ⓐ\(−3\) ⓑ 2 ⓒ 3
Ahora estamos listos para evaluar un\(3×3\) determinante. Para ello ampliamos por menores, lo que nos permite evaluar el\(3×3\) determinante usando\(2×2\) determinantes, ¡que ya sabemos evaluar!
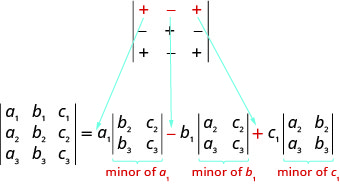
Para evaluar un\(3×3\) determinante expandiendo por menores a lo largo de la primera fila, utilizamos el siguiente patrón:
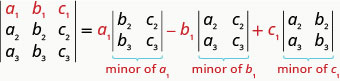
Recuerda, para encontrar el menor de una entrada eliminamos la fila y columna que contiene la entrada.
Para evaluar un\(3×3\) determinante expandiendo por menores a lo largo de la primera fila, el siguiente patrón:
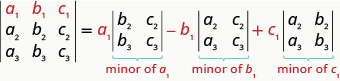
Evaluar el determinante expandiendo\(\left| \begin{matrix} 2&−3&−1\\3&2&0\\−1&−1&−2 \end{matrix} \right|\) por menores a lo largo de la primera fila.
- Contestar
-

Ampliar por menores a lo largo de la primera fila 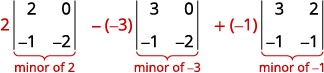
Evaluar cada determinante. 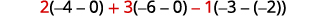
Simplificar. 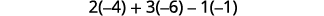
Simplificar. 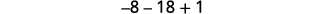
Simplificar. 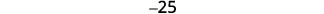
Evaluar el determinante\(\left| \begin{matrix} 3&−2&4\\0&−1&−2\\2&3&−1 \end{matrix} \right|\), expandiendo por menores a lo largo de la primera fila.
- Contestar
-
37
Evaluar el determinante\(\left| \begin{matrix} 3&−2&−2\\2&−1&4\\−1&0&−3 \end{matrix} \right|\), expandiendo por menores a lo largo de la primera fila.
- Contestar
-
7
Para evaluar un\(3×3\) determinante podemos ampliar por menores usando cualquier fila o columna. Elegir una fila o columna que no sea la primera fila a veces facilita el trabajo.
Cuando expandimos por cualquier fila o columna, debemos tener cuidado con el signo de los términos en la expansión. Para determinar el signo de los términos, utilizamos la siguiente tabla de patrones de signos.
\[\left| \begin{matrix} +&−&+\\−&+&−\\+&−&+ \end{matrix} \right|\nonumber\]
Al expandirse por menores usando una fila o columna, el signo de los términos en la expansión sigue el siguiente patrón. \[\left| \begin{matrix} +&−&+\\−&+&−\\+&−&+ \end{matrix} \right|\nonumber\]
Observe que el patrón de signos en la primera fila coincide con los signos entre los términos de la expansión por la primera fila.
Ya que podemos expandirnos por cualquier fila o columna, ¿cómo decidimos qué fila o columna usar? Por lo general tratamos de escoger una fila o columna que nos facilite el cálculo. Si el determinante contiene un 0, el uso de la fila o columna que contiene el 0 facilitará los cálculos.
Evaluar el determinante\(\left| \begin{matrix} 4&−1&−3\\3&0&2\\5&−4&−3 \end{matrix} \right|\) expandiendo por menores.
- Contestar
-
Para ampliar por menores, buscamos una fila o columna que facilite nuestros cálculos. Dado que 0 está en la segunda fila y en la segunda columna, expandirse por cualquiera de ellas es una buena opción. Dado que la segunda fila tiene menos negativos que la segunda columna, vamos a expandirnos por la segunda fila.

Expandir usando la segunda fila. Tenga cuidado con las señales. 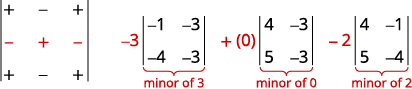
Evaluar cada determinante. 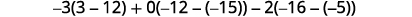
Simplificar. 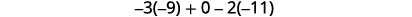
Simplificar. 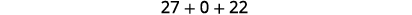
Agregar. 
Evaluar el determinante\(\left| \begin{matrix} 2&−1&−3\\0&3&−4\\3&−4&−3 \end{matrix} \right|\) expandiendo por menores.
- Contestar
-
\(−11\)
Evaluar el determinante\(\left| \begin{matrix} −2&−1&−3\\−1&2&2\\4&−4&0 \end{matrix} \right|\) expandiendo por menores.
- Contestar
-
8
Usa la Regla de Cramer para Resolver Sistemas de Ecuaciones
La Regla de Cramer es un método para resolver sistemas de ecuaciones utilizando determinantes. Se puede derivar resolviendo la forma general de los sistemas de ecuaciones por eliminación. Aquí demostraremos la regla para ambos sistemas de dos ecuaciones con dos variables y para sistemas de tres ecuaciones con tres variables.
Empecemos con los sistemas de dos ecuaciones con dos variables.
Para el sistema de ecuaciones\(\left\{\begin{array} {l} a_1x+b_1y=k_1 \\ a_2x+b_2y=k_2\end{array}\right.\), la solución\((x,y)\) puede ser determinada por

Observe que para formar el determinante D, utilizamos tomar los coeficientes de las variables.
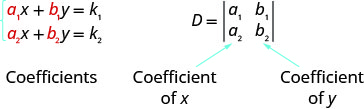
Observe que para formar el determinante\(D_x\) y\(D_y\), sustituimos las constantes por los coeficientes de la variable que estamos encontrando.
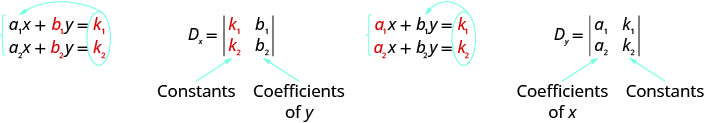
Resuelve usando la regla de Cramer:\(\left\{ \begin{array} {l} 2x+y=−4\\3x−2y=−6\end{array}\right.\)
- Contestar
-






Resuelve usando la regla de Cramer:\(\left\{\begin{array} {l} 3x+y=−3 \\ 2x+3y=6 \end{array} \right.\)
- Contestar
-
\((−\frac{15}{7},\frac{24}{7})\)
Resuelve usando la regla de Cramer:\(\left\{\begin{array} {l} −x+y=2\\2x+y=−4 \end{array} \right.\)
- Contestar
-
\((−2,0)\)
- Evaluar el determinante D, utilizando los coeficientes de las variables.
- Evaluar el determinante\(D_x\). Utilice las constantes en lugar de los coeficientes x.
- Evaluar el determinante\(D_y\). Utilice las constantes en lugar de los coeficientes y.
- Encuentra x e y. \(x=\frac{D_x}{D}\),\(y=\frac{D_y}{D}\)
- Escribe la solución como un par ordenado.
- Comprobar que el par ordenado es una solución a ambas ecuaciones originales.
Para resolver un sistema de tres ecuaciones con tres variables con la Regla de Cramer, básicamente hacemos lo que hicimos para un sistema de dos ecuaciones. Sin embargo, ahora tenemos que resolver tres variables para obtener la solución. ¡También van a ser los determinantes\(3×3\) que harán que nuestro trabajo sea más interesante!
Para el sistema de ecuaciones\(\left\{\begin{array} {l} a_1x+b_1y+c_1z=k_1\\a_2x+b_2y+c_2z=k_2\\a_3x+b_3y+c_3z=k_3\end{array}\right.\), la solución\((x,y,z)\) puede ser determinada por

Resuelve el sistema de ecuaciones usando la Regla de Cramer:\(\left\{\begin{array} {l} 3x−5y+4z=5\\5x+2y+z=0\\2x+3y−2z=3 \end{array} \right.\)
- Contestar
-
Evaluar el determinante D. 
Ampliar por menores usando la columna 1. 
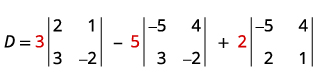
Evaluar los determinantes. 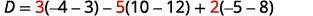
Simplificar. 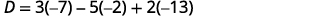
Simplificar. 
Simplificar. 
Evaluar el determinante\(D_x\). Utilice las
constantes para reemplazar los coeficientes de x.
Ampliar por menores usando la columna 1. 
Evaluar los determinantes. 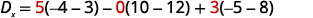
Simplificar. 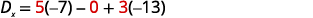
Simplificar. 
Evaluar el determinante Dy.Dy. Utilice las
constantes para reemplazar los coeficientes de y.

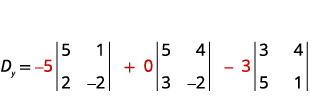
Evaluar los determinantes. 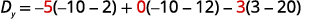
Simplificar. 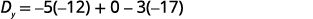
Simplificar. 
Simplificar. 
Evaluar el determinante Dz.Dz. Utilice las
constantes para reemplazar los coeficientes de z.

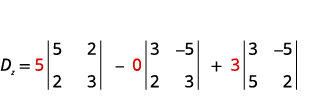
Evaluar los determinantes. 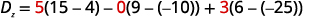
Simplificar. 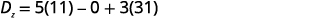
Simplificar. 
Simplificar. 
Encuentra x, y y z. 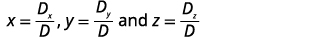
Sustituto en los valores. 
Simplificar. 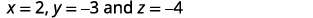
Escribe la solución como un triple ordenado. 
Verifique que el triple ordenado sea una solución
a las tres ecuaciones originales.Te dejamos el cheque a ti. La solución es\((2,−3,−4)\).
Resuelve el sistema de ecuaciones usando la Regla de Cramer:\(\left\{\begin{array} {l} 3x+8y+2z=−5\\2x+5y−3z=0\\x+2y−2z=−1 \end{array} \right.\)
- Contestar
-
\((−9,3,−1)\)
Resuelve el sistema de ecuaciones usando la Regla de Cramer:\(\left\{\begin{array} {l} 3x+y−6z=−3\\2x+6y+3z=0\\3x+2y−3z=−6 \end{array} \right.\)
- Contestar
-
\((−6,3,−2)\)
La regla de Cramer no funciona cuando el valor del determinante D es 0, ya que esto significaría que estaríamos dividiendo por 0. Pero cuando\(D=0\), el sistema es inconsistente o dependiente.
Cuando el valor de\(D=0\) y\(D_x,\space D_y\) y D son todos cero, el sistema es consistente y dependiente y hay infinitamente muchas soluciones.
Cuando el valor de\(D=0\) y\(D_x,\space D_y\) y no\(D_z\) son todos cero, el sistema es inconsistente y no hay solución.
Para cualquier sistema de ecuaciones, donde el valor del determinante\(D=0\),
\[ \begin{array} {lll} \textbf{Value of determinants} &\textbf{Type of system} &\textbf{Solution} \\ {D=0\text{ and }D_x,\space D_y\text{ and }D_z\text{ are all zero}} &\text{consistent and dependent} &\text{infinitely many solutions} \\ {D=0\text{ and }D_x,\space D_y\text{ and }D_z\text{ are not all zero}} &\text{inconsistent} &\text{no solution} \end{array} \nonumber\]
En el siguiente ejemplo, utilizaremos los valores de los determinantes para encontrar la solución del sistema.
Resuelve el sistema de ecuaciones usando la regla de Cramer:\(\left\{\begin{array} {l} x+3y=4\\−2x−6y=3 \end{array} \right.\)
- Contestar
-
\(\begin{array} {ll} {} &{\left\{\begin{array} {l} x+3y=4\\−2x−6y=3 \end{array} \right.} \\ {\begin{array} {l} \text{Evaluate the determinantD,using the} \\ \text{coefficients of the variables.} \end{array}} &{D=\left|\begin{matrix} 1&3\\−2&−6\end{matrix}\right|} \\ {} &{D=−6−(−6)} \\ {} &{D=0} \end{array} \)
No podemos usar la Regla de Cramer para resolver este sistema. Pero al mirar el valor de los determinantes\(D_x\) y\(D_y\), podemos determinar si el sistema es dependiente o inconsistente.
\(\begin{array} {ll} {\text{Evaluate the determinant }D_x.} &{D_x=\left|\begin{matrix} 4&3\\3&−6\end{matrix}\right|} \\ {} &{D_x=−24−9} \\ {} &{D_x=15} \end{array} \)
Dado que todos los determinantes no son cero, el sistema es inconsistente. No hay solución.
Resuelve el sistema de ecuaciones usando la regla de Cramer:\(\left\{\begin{array} {l} 4x−3y=8\\8x−6y=14 \end{array} \right.\)
- Contestar
-
no hay solución
Resuelve el sistema de ecuaciones usando la regla de Cramer:\(\left\{\begin{array} {l} x=−3y+4\\2x+6y=8 \end{array} \right.\)
- Contestar
-
infinitas soluciones
Resolver aplicaciones usando determinantes
Una interesante aplicación de determinantes nos permite probar si los puntos son colineales. Tres puntos\((x_1,y_1)\),\((x_2,y_2)\) y\((x_3,y_3)\) son colineales si y sólo si el determinante abajo es cero.
\[\left|\begin{matrix}x_1&y_1&1\\x_2&y_2&1\\x_3&y_3&1\end{matrix}\right|=0\nonumber\]
Tres puntos\((x_1,y_1)\),\((x_2,y_2)\) y\((x_3,y_3)\) son colineales si y solo si
\[\left|\begin{matrix}x_1&y_1&1\\x_2&y_2&1\\x_3&y_3&1\end{matrix}\right|=0\nonumber\]
Utilizaremos esta propiedad en el siguiente ejemplo.
Determinar si los puntos\((5,−5)\),\((4,−3)\), y\((3,−1)\) son colineales.
- Contestar
-
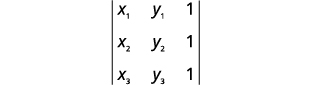
Sustituir los valores en el determinante.
\((5,−5)\),\((4,−3)\), y\((3,−1)\)
Evaluar el determinante expandiendo
por menores usando la columna 3.
Evaluar los determinantes. 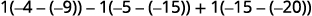
Simplificar. 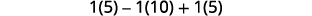
Simplificar. 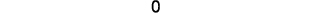
El valor del determinado es 0, por lo que los
puntos son colineales.
Determinar si los puntos\((3,−2)\),\((5,−3)\), y\((1,−1)\) son colineales.
- Contestar
-
si
Determinar si los puntos\((−4,−1)\),\((−6,2)\), y\((−2,−4)\) son colineales.
- Contestar
-
si
Acceda a estos recursos en línea para obtener instrucción y práctica adicionales con la resolución de sistemas de desigualdades lineales mediante gráficos.
- Resolver sistemas de desigualdades lineales mediante gráficos
- Sistemas de Desigualdades Lineales
Conceptos clave
- Determinante: El determinante de cualquier matriz cuadrada\(\left[\begin{matrix}a&b\\c&d\end{matrix}\right]\), donde a, b, c y d son números reales, es
\[\left|\begin{matrix}a&b\\c&d\end{matrix}\right|=ad−bc\nonumber\]
- Ampliar por menores a lo largo de la primera fila para evaluar un determinante de 3 × 3: Para evaluar un\(3×3\) determinante expandiendo por menores a lo largo de la primera fila, el siguiente patrón:
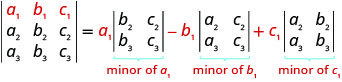
- Patrón de señal: Al expandirse por menores usando una fila o columna, el signo de los términos en la expansión sigue el siguiente patrón.
\[\left|\begin{matrix}+&−&+\\−&+&−\\+&−&+\end{matrix}\right|\nonumber\]
- Regla de Cramer: Para el sistema de ecuaciones\(\left\{\begin{array} {l} a_1x+b_1y=k_1\\a_2x+b_2y=k_2\end{array}\right.\), la solución\((x,y)\) puede ser determinada por

Aviso que para formar el determinante D, usamos tomar los coeficientes de las variables. - Cómo resolver un sistema de dos ecuaciones usando la regla de Cramer.
- Evaluar el determinante D, utilizando los coeficientes de las variables.
- Evaluar el determinante\(D_x\). Utilice las constantes en lugar de los coeficientes x.
- Evaluar el determinante\(D_y\). Utilice las constantes en lugar de los coeficientes y.
- Encuentra x e y. \(x=\frac{D_x}{D}\),\(y=\frac{D_y}{D}\).
- Escribe la solución como un par ordenado.
- Comprobar que el par ordenado es una solución a ambas ecuaciones originales.
- Sistemas de Ecuaciones Dependientes e Inconsistentes: Para cualquier sistema de ecuaciones, donde el valor del determinante\(D=0\),\[ \begin{array} {lll} \textbf{Value of determinants} &\textbf{Type of system} &\textbf{Solution} \\ {D=0\text{ and }D_x,\space D_y\text{ and }D_z\text{ are all zero}} &\text{consistent and dependent} &\text{infinitely many solutions} \\ {D=0\text{ and }D_x,\space D_y\text{ and }D_z\text{ are not all zero}} &\text{inconsistent} &\text{no solution} \end{array} \nonumber\]
- Prueba para puntos colineales: Tres puntos\((x_1,y_1)\)\((x_2,y_2)\), y\((x_3,y_3)\) son colineales si y solo si
\[\left|\begin{matrix}x_1&y_1&1\\x_2&y_2&1\\x_3&y_3&1\end{matrix}\right|=0\nonumber\]
Glosario
- determinante
- Cada matriz cuadrada tiene un número real asociado a ella llamado su determinante.
- menor de una entrada en un determinante 3×33×3
- El menor de una entrada en un determinante 3×33×3 es el determinante 2×22×2 encontrado al eliminar la fila y columna en el determinante 3×33×3que contiene la entrada.
- matriz cuadrada
- Una matriz cuadrada es una matriz con el mismo número de filas y columnas.


