6.2: Mayor factor común y factor por agrupación
- Page ID
- 112430
Al final de esta sección, podrás:
- Encuentra el mayor factor común de dos o más expresiones
- Factor el mayor factor común de un polinomio
- Factor por agrupación
Encuentra el factor común más grande de dos o más expresiones
Antes multiplicamos factores juntos para obtener un producto. Ahora, invertiremos este proceso; comenzaremos con un producto y luego lo descompondremos en sus factores. Dividir un producto en factores se llama factorización.
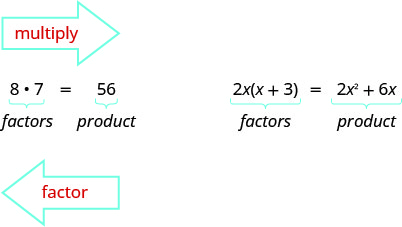
Hemos aprendido a factorizar números para encontrar el múltiplo menos común (MCM) de dos o más números. Ahora vamos a factorizar expresiones y encontrar el mayor factor común de dos o más expresiones. El método que utilizamos es similar al que usamos para encontrar el LCM.
El mayor factor común (GCF) de dos o más expresiones es la expresión más grande que es un factor de todas las expresiones.
Resumimos los pasos que utilizamos para encontrar el mayor factor común.
- Factorizar cada coeficiente en primos. Escribe todas las variables con exponentes en forma expandida.
- Enumere todos los factores: coincidan con los factores comunes en una columna. En cada columna, circule los factores comunes.
- Derribar los factores comunes que comparten todas las expresiones.
- Multiplicar los factores.
El siguiente ejemplo nos mostrará los pasos para encontrar el mayor factor común de tres expresiones.
Encuentra el mayor factor común de\(21x^3,\space 9x^2,\space 15x\).
- Contestar
-
Factorizar cada coeficiente en primos y escribir las variables con exponentes en forma expandida. Encierra en un círculo los factores comunes en cada columna. Derribar los factores comunes. 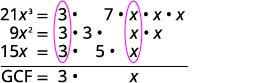
Multiplicar los factores. GCF\(=3x\) El GCF de\(21x^3\),\(9x^2\) y\(15x\) es\(3x\).
Encuentra el mayor factor común:\(25m^4,\space 35m^3,\space 20m^2.\)
- Contestar
-
\(5m^2\)
Encuentra el mayor factor común:\(14x^3,\space 70x^2,\space 105x\).
- Contestar
-
\(7x\)
Factor el mayor factor común de un polinomio
A veces es útil representar un número como producto de factores, por ejemplo, 12 como\(2·6\) o\(3·4\). En álgebra, también puede ser útil para representar un polinomio en forma factorizada. Comenzaremos con un producto, como\(3x^2+15x\), y terminaremos con sus factores,\(3x(x+5)\). Para ello aplicamos la Propiedad Distributiva “a la inversa”.
Aquí señalamos la Propiedad Distributiva tal como la viste en capítulos anteriores y “a la inversa”.
Si a, b y c son números reales, entonces
\[a(b+c)=ab+ac \quad \text{and} \quad ab+ac=a(b+c)\nonumber\]
El formulario de la izquierda se utiliza para multiplicar. El formulario de la derecha se utiliza para factorizar.
Entonces, ¿cómo se utiliza la Propiedad Distributiva para factorizar un polinomio? ¡Simplemente encuentra el GCF de todos los términos y escribe el polinomio como producto!
Factor:\(8m^3−12m^2n+20mn^2\).
- Contestar
-




Factor:\(9xy^2+6x^2y^2+21y^3\).
- Contestar
-
\(3y^2(3x+2x^2+7y)\)
Factor:\(3p^3−6p^2q+9pq^3\).
- Contestar
-
\(3p(p^2−2pq+3q^3)\)
- Encuentra el GCF de todos los términos del polinomio.
- Reescribe cada término como un producto usando el GCF.
- Utilice la Propiedad Distributiva “inversa” para factorizar la expresión.
- Verificar multiplicando los factores.
Usamos “factor” como sustantivo y verbo:
\[\begin{array} {ll} \text{Noun:} &\hspace{50mm} 7 \text{ is a factor of }14 \\ \text{Verb:} &\hspace{50mm} \text{factor }3 \text{ from }3a+3\end{array}\nonumber\]
Factor:\(5x^3−25x^2\).
- Contestar
-
Encuentre el GCF de\(5x^3\) y\(25x^2\). 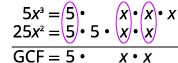
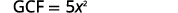
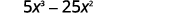
Reescribir cada término. 
Facturar el GCF. 
Comprobar:
\[5x^2(x−5) \nonumber\]\[5x^2·x−5x^2·5 \nonumber\]
\[5x^3−25x^2 \checkmark\nonumber\]
Factor:\(2x^3+12x^2\).
- Contestar
-
\(2x^2(x+6)\)
Factor:\(6y^3−15y^2\).
- Contestar
-
\(3y^2(2y−5)\)
Factor:\(8x^3y−10x^2y^2+12xy^3\).
- Contestar
-
El GCF de\(8x^3y,\space −10x^2y^2,\) y\(12xy^3\)
es\(2xy\).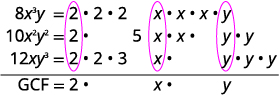

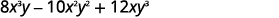
Reescribir cada término usando el GCF,\(2xy\). 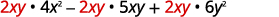
Facturar el GCF. 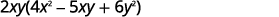
Comprobar:
\[2xy(4x^2−5xy+6y^2)\nonumber\]\[2xy·4x^2−2xy·5xy+2xy·6y^2\nonumber\]
\[8x^3y−10x^2y^2+12xy^3\checkmark\nonumber\]
Factor:\(15x^3y−3x^2y^2+6xy^3\).
- Contestar
-
\(3xy(5x^2−xy+2y^2)\)
Factor:\(8a^3b+2a^2b^2−6ab^3\).
- Contestar
-
\(2ab(4a^2+ab−3b^2)\)
Cuando el coeficiente principal es negativo, factorizamos lo negativo como parte del GCF.
Factor:\(−4a^3+36a^2−8a\).
- Contestar
-
El coeficiente principal es negativo, por lo que el GCF será negativo.
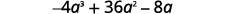
Reescribir cada término usando el GCF,\(−4a\). 
Facturar el GCF. 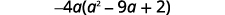
Comprobar:
\[−4a(a^2−9a+2)\nonumber\]\[−4a·a^2−(−4a)·9a+(−4a)·2\nonumber\]
\[−4a^3+36a^2−8a\checkmark\nonumber\]
Factor:\(−4b^3+16b^2−8b\).
- Contestar
-
\(−4b(b^2−4b+2)\)
Factor:\(−7a^3+21a^2−14a\).
- Contestar
-
\(−7a(a^2−3a+2)\)
Hasta ahora nuestros mayores factores comunes han sido los monomios. En el siguiente ejemplo, el mayor factor común es un binomio.
Factor:\(3y(y+7)−4(y+7)\).
- Contestar
-
El GCF es el binomio\(y+7\).
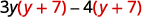
Factorizar el GCF,\((y+7)\). \((y+7)(3 y-4)\) Verifica por tu cuenta multiplicando.
Factor:\(4m(m+3)−7(m+3)\).
- Contestar
-
\((m+3)(4m−7)\)
Factor:\(8n(n−4)+5(n−4)\).
- Contestar
-
\((n−4)(8n+5)\)
Factor por Agrupación
A veces no hay un factor común de todos los términos de un polinomio. Cuando hay cuatro términos separamos el polinomio en dos partes con dos términos en cada parte. Entonces busca el GCF en cada parte. Si el polinomio puede ser factorizado, encontrarás un factor común que emerge de ambas partes. No todos los polinomios pueden ser factorizados. Al igual que algunos números son primos, algunos polinomios son primos.
Factor por agrupación:\(xy+3y+2x+6\).
- Contestar
-




Factor por agrupación:\(xy+8y+3x+24\).
- Contestar
-
\((x+8)(y+3)\)
Factor por agrupación:\(ab+7b+8a+56\).
- Contestar
-
\((a+7)(b+8)\)
- Términos de grupo con factores comunes.
- Factorizar el factor común en cada grupo.
- Factorizar el factor común a partir de la expresión.
- Verificar multiplicando los factores.
Factor por agrupación: ⓐ\(x^2+3x−2x−6\) ⓑ\(6x^2−3x−4x+2\).
- Responder
-
ⓐ
\(\begin{array} {ll} \text{There is no GCF in all four terms.} &x^2+3x−2x−6 \\ \text{Separate into two parts.} &x^2+3x\quad −2x−6 \\ \begin{array} {l} \text{Factor the GCF from both parts. Be careful} \\ \text{with the signs when factoring the GCF from} \\ \text{the last two terms.} \end{array} &x(x+3)−2(x+3) \\ \text{Factor out the common factor.} &(x+3)(x−2) \\ \text{Check on your own by multiplying.} & \end{array}\)
ⓑ
\(\begin{array} {ll} \text{There is no GCF in all four terms.} &6x^2−3x−4x+2 \\ \text{Separate into two parts.} &6x^2−3x\quad −4x+2\\ \text{Factor the GCF from both parts.} &3x(2x−1)−2(2x−1) \\ \text{Factor out the common factor.} &(2x−1)(3x−2) \\ \text{Check on your own by multiplying.} & \end{array}\)
Factor por agrupación: ⓐ\(x^2+2x−5x−10\) ⓑ\(20x^2−16x−15x+12\).
- Responder
-
ⓐ\((x−5)(x+2)\)
ⓑ\((5x−4)(4x−3)\)
Factor por agrupación: ⓐ\(y^2+4y−7y−28\) ⓑ\(42m^2−18m−35m+15\).
- Responder
-
ⓐ\((y+4)(y−7)\)
ⓑ\((7m−3)(6m−5)\)
Conceptos clave
- Cómo encontrar el mayor factor común (GCF) de dos expresiones.
- Factorizar cada coeficiente en primos. Escribe todas las variables con exponentes en forma expandida.
- Enumere todos los factores: coincidan con los factores comunes en una columna. En cada columna, circule los factores comunes.
- Derribar los factores comunes que comparten todas las expresiones.
- Multiplicar los factores.
- Propiedad distributiva: Si\(a\),\(b\) y\(c\) son números reales, entonces
\[a(b+c)=ab+ac\quad \text{and}\quad ab+ac=a(b+c)\nonumber\]
El formulario de la izquierda se utiliza para multiplicar. El formulario de la derecha se utiliza para factorizar. - Cómo factorizar el mayor factor común a partir de un polinomio.
- Encuentra el GCF de todos los términos del polinomio.
- Reescribe cada término como un producto usando el GCF.
- Utilice la Propiedad Distributiva “inversa” para factorizar la expresión.
- Verificar multiplicando los factores.
- Factor como sustantivo y verbo: Utilizamos “factor” tanto como sustantivo como verbo.
\[\begin{array} {ll} \text{Noun:} &\quad 7 \text{ is a factor of } 14\\ \text{Verb:} &\quad \text{factor }3 \text{ from }3a+3\end{array}\nonumber\]
- Cómo factorizar por agrupación.
- Términos de grupo con factores comunes.
- Factorizar el factor común en cada grupo.
- Factorizar el factor común a partir de la expresión.
- Verificar multiplicando los factores.
Glosario
- factorización
- La división de un producto en factores se llama factorización.
- mayor factor común
- El mayor factor común (GCF) de dos o más expresiones es la expresión más grande que es un factor de todas las expresiones.


