6.4: Factor Productos Especiales
- Page ID
- 112445
Al final de esta sección, podrás:
- Trinomios cuadrados perfectos
- Diferencias factoriales de cuadrados
- Sumas de factores y diferencias de cubos
Antes de comenzar, toma este cuestionario de preparación.
- Simplificar:\((3x^2)^3\).
- Multiplicar:\((m+4)^2\).
- Multiplicar:\((x−3)(x+3)\).
Hemos visto que algunos binomios y trinomios resultan de productos especiales: binomios al cuadrado y multiplicación de conjugados. Si aprendes a reconocer este tipo de polinomios, puedes usar los patrones de productos especiales para factorizarlos mucho más rápidamente.
Trinomios cuadrados perfectos de factor
Algunos trinomios son cuadrados perfectos. Resultan de multiplicar un binomio por sí mismo. Cuadramos un binomio usando el patrón Cuadrados Binomiales en un capítulo anterior.
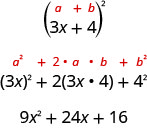
Al trinomio\(9x^2+24x+16\) se le llama trinomio cuadrado perfecto. Es el cuadrado del binomio\(3x+4\).
En este capítulo, comenzarás con un trinomio cuadrado perfecto y lo factorizarás en sus factores primos. Se podría factorizar este trinomio utilizando los métodos descritos en la última sección, ya que es de la forma\(ax^2+bx+c\). Pero si reconoces que el primer y último término son cuadrados y el trinomio se ajusta al patrón perfecto de trinomios cuadrados, te ahorrarás mucho trabajo. Aquí está el patrón, el reverso del patrón de cuadrados binomiales.
Si\(a\) y\(b\) son números reales
\[a^2+2ab+b^2=(a+b)^2\nonumber\]
\[a^2−2ab+b^2=(a−b)^2\nonumber\]
Para hacer uso de este patrón, hay que reconocer que un trinomio dado le encaja. Verifique primero para ver si el coeficiente inicial es un cuadrado perfecto,\(a^2\). Siguiente comprobar que el último término es un cuadrado perfecto,\(b^2\). Entonces revisa el término medio, ¿es el producto,\(2ab\)? Si todo lo comprueba, puedes escribir fácilmente los factores.
Factor:\(9x^2+12x+4\).
- Responder
-



Factor:\(4x^2+12x+9\).
- Responder
-
\((2x+3)^2\)
Factor:\(9y^2+24y+16\).
- Responder
-
\((3y+4)^2\)
El signo del término medio determina qué patrón usaremos. Cuando el término medio es negativo, usamos el patrón\(a^2−2ab+b^2\), que factores a\((a−b)^2\).
Aquí se resumen los pasos.
\(\begin{array} {lllll} \textbf{Step 1.} &\text{Does the trinomial fit the pattern?} &\quad &\hspace{7mm} a^2+2ab+b^2 &\hspace{7mm} a^2−2ab+b^2 \\ &\text{Are the first and last terms perfect squares?} &\quad & &\\ &\text{Write them as squares.} &\quad &\hspace{5mm}(a)^2\hspace{16mm} (b)^2 &\hspace{6mm}(a)^2\hspace{16mm} (b)^2 \\ &\text{Check the middle term. Is it }2ab? &\quad &\hspace{12mm} {\,}^{\searrow}{\,}_{2·a·b}{\,}^{\swarrow} &\hspace{12mm} {\,}^{\searrow}{\,}_{2·a·b}{\,}^{\swarrow} \\ \textbf{Step 2.} &\text{Write the square of the binomial.} &\quad &\hspace{13mm} (a+b)^2 &\hspace{13mm} (a−b)^2 \\ \textbf{Step 3.} &\text{Check by multiplying.} & & & \end{array}\)
Trabajaremos uno ahora donde el término medio sea negativo.
Factor:\(81y^2−72y+16\).
- Responder
-
El primer y último término son cuadrados. Ver si el término medio se ajusta al patrón de un trinomio cuadrado perfecto. El término medio es negativo, por lo que el cuadrado binomial lo sería\((a−b)^2\).
\(81 y^{2}-72 y+16\) ¿Los primeros y últimos términos son cuadrados perfectos? 
Consulta el término medio. 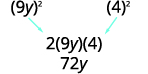
¿Coincide\((a−b)^2\)? Sí. 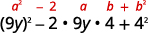
Escribir como el cuadrado de un binomio. \((9 y-4)^{2}\) Verificar multiplicando:
\[(9y−4)^2\nonumber\]\[(9y)^2−2·9y·4+4^2\nonumber\]\[81y^2−72y+16\checkmark\nonumber\]
Factor:\(64y^2−80y+25\).
- Responder
-
\((8y−5)^2\)
Factor:\(16z^2−72z+81\).
- Responder
-
\((4z−9)^2\)
El siguiente ejemplo será un trinomio cuadrado perfecto con dos variables.
Factor:\(36x^2+84xy+49y^2\).
- Responder
-
\(36 x^{2}+84 x y+49 y^{2}\) Pruebe cada término para verificar el patrón. 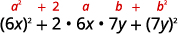
Factor. \((6 x+7 y)^{2}\) Verificar multiplicando.
\[(6x+7y)^2\nonumber\]\[(6x)^2+2·6x·7y+(7y)^2\nonumber\]\[36x^2+84xy+49y^2\checkmark\nonumber\]
Factor:\(49x^2+84xy+36y^2\).
- Responder
-
\((7x+6y)^2\)
Factor:\(64m^2+112mn+49n^2\).
- Responder
-
\((8m+7n)^2\)
Recuerde que el primer paso en la factorización es buscar un mayor factor común. Los trinomios cuadrados perfectos pueden tener un GCF en los tres términos y debe tenerse en cuenta primero. Y, a veces, una vez factorizado el GCF, reconocerás un trinomio cuadrado perfecto.
Factor:\(100x^2y−80xy+16y\).
- Responder
-
\(100 x^{2} y-80 x y+16 y\) ¿Existe un GCF? Sí\(4y\), así que factírelo. \(4 y\left(25 x^{2}-20 x+4\right)\) ¿Es este un trinomio cuadrado perfecto? Verificar el patrón. 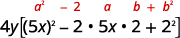
Factor. \(4 y(5 x-2)^{2}\) Recuerde: Mantener el factor 4 y en el producto final. Comprobar:
\[4y(5x−2)^2\nonumber\]\[4y[(5x)2−2·5x·2+22]\nonumber\]\[4y(25x2−20x+4)\nonumber\]100x2y−80xy+16y\ marca de verificación\]
Factor:\(8x^2y−24xy+18y\).
- Responder
-
\(2y(2x−3)^2\)
Factor:\(27p^2q+90pq+75q\).
- Responder
-
\(3q(3p+5)^2\)
Diferencias factoriales de cuadrados
El otro producto especial que viste en el capítulo anterior fue el patrón Producto de Conconjugados. Se utilizó esto para multiplicar dos binomios que eran conjugados. Aquí hay un ejemplo:
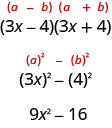
Una diferencia de factores cuadrados a un producto de conjugados.
Si\(a\) y\(b\) son números reales,
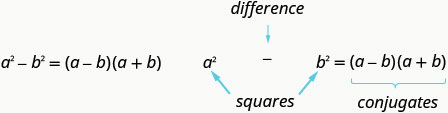
Recuerde, “diferencia” se refiere a la resta. Entonces, para usar este patrón debes asegurarte de tener un binomio en el que se están restando dos cuadrados.
Factor:\(64y^2−1\).
- Responder
-




Factor:\(121m^2−1\).
- Responder
-
\((11m−1)(11m+1)\)
Factor:\(81y^2−1\).
- Responder
-
\((9y−1)(9y+1)\)
\(\begin{array} {llll} \textbf{Step 1.} &\text{Does the binomial fit the pattern?} &\qquad &\hspace{5mm} a^2−b^2 \\ &\text{Is this a difference?} &\qquad &\hspace{2mm} \text{____−____} \\ &\text{Are the first and last terms perfect squares?} & & \\ \textbf{Step 2.} &\text{Write them as squares.} &\qquad &\hspace{3mm} (a)^2−(b)^2 \\ \textbf{Step 3.} &\text{Write the product of conjugates.} &\qquad &(a−b)(a+b) \\ \textbf{Step 4.} &\text{Check by multiplying.} & & \end{array}\)
Es importante recordar que las sumas de cuadrados no factorizan en un producto de binomios. No hay factores binomiales que se multipliquen juntos para obtener una suma de cuadrados. Después de eliminar cualquier GCF, ¡la expresión\(a^2+b^2\) es prime!
El siguiente ejemplo muestra variables en ambos términos.
Factor:\(144x^2−49y^2\).
- Responder
-
\(\begin{array} {lll} &\quad &144x^2−49y^2 \\ \text{Is this a difference of squares? Yes.} &\quad &(12x)^2−(7y)^2 \\ \text{Factor as the product of conjugates.} &\quad &(12x−7y)(12x+7y) \\ \text{Check by multiplying.} &\quad &(12x−7y)(12x+7y) \\ \text{Check by multiplying.} &\quad & \\ &\quad & \\ &\quad & \\ \hspace{14mm} (12x−7y)(12x+7y) &\quad & \\ \hspace{21mm} 144x^2−49y^2\checkmark &\quad & \end{array}\)
Factor:\(196m^2−25n^2\).
- Responder
-
\((14m−5n)(14m+5n)\)
Factor:\(121p^2−9q^2\).
- Responder
-
\((11p−3q)(11p+3q)\)
Como siempre, primero debes buscar un factor común cada vez que tengas una expresión a factor. A veces un factor común puede “disfrazar” la diferencia de cuadrados y no reconocerás los cuadrados perfectos hasta que factorices el GCF.
Además, para factorizar completamente el binomio en el siguiente ejemplo, ¡factorizaremos una diferencia de cuadrados dos veces!
Factor:\(48x^4y^2−243y^2\).
- Responder
-
\(\begin{array} {ll} &48x^4y^2−243y^2 \\ \text{Is there a GCF? Yes, }3y^2\text{—factor it out!} &3y^2(16x^4−81) \\ \text{Is the binomial a difference of squares? Yes.} &3y^2\left((4x^2)^2−(9)^2\right) \\ \text{Factor as a product of conjugates.} &3y^2(4x^2−9)(4x^2+9) \\ \text{Notice the first binomial is also a difference of squares!} &3y^2((2x)^2−(3)^2)(4x^2+9) \\ \text{Factor it as the product of conjugates.} &3y^2(2x−3)(2x+3)(4x^2+9) \end{array}\)
El último factor, la suma de cuadrados, no se puede factorizar.
\(\begin{array} {l} \text{Check by multiplying:} \\ \hspace{10mm} 3y^2(2x−3)(2x+3)(4x^2+9) \\ \\ \\ \hspace{15mm} 3y^2(4x^2−9)(4x^2+9) \\ \hspace{20mm} 3y^2(16x^4−81) \\ \hspace{19mm} 48x^4y^2−243y^2\checkmark\end{array}\)
Factor:\(2x^4y^2−32y^2\).
- Responder
-
\(2y^2(x−2)(x+2)(x^2+4)\)
Factor:\(7a^4c^2−7b^4c^2\).
- Responder
-
\(7c^2(a−b)(a+b)(a^2+b^2)\)
El siguiente ejemplo tiene un polinomio con 4 términos. Hasta el momento, cuando esto ocurrió agrupamos los términos en dos y factorizamos a partir de ahí. Aquí notaremos que los tres primeros términos forman un trinomio cuadrado perfecto.
Factor:\(x^2−6x+9−y^2\).
- Responder
-
Observe que los tres primeros términos forman un trinomio cuadrado perfecto.
\(x^{2}-6 x+9-y^{2}\) Factorizar agrupando los tres primeros términos. \(\underbrace{x^{2}-6 x+9} - y^{2}\) Usa el patrón trinomio cuadrado perfecto. \((x-3)^{2}-y^{2}\) ¿Es esto una diferencia de cuadrados? Sí. Sí, escríbelos como cuadrados. 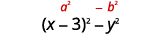
Factor como producto de conjugados. 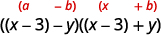
\((x-3-y)(x-3+y)\) Es posible que desee reescribir la solución como\((x−y−3)(x+y−3)\).
Factor:\(x^2−10x+25−y^2\).
- Responder
-
\((x−5−y)(x−5+y)\)
Factor:\(x^2+6x+9−4y^2\).
- Responder
-
\((x+3−2y)(x+3+2y)\)
Sumas de Factores y Diferencias de Cubos
Hay otro patrón especial para factorizar, uno que no usamos cuando multiplicamos polinomios. Este es el patrón para la suma y diferencia de cubos. Primero escribiremos estas fórmulas y luego las revisaremos por multiplicación.
\[a^3+b^3=(a+b)(a^2−ab+b^2\nonumber\]
\[a^3−b^3=(a−b)(a^2+ab+b^2)\nonumber\]
Revisaremos el primer patrón y te dejaremos el segundo a ti.
| \(\color{red}(a+b) \color{black} \left(a^{2}-a b+b^{2}\right)\) | |
| Distribuir. | \(\color{red}a \color{black}\left(a^{2}-a b+b^{2}\right)+ \color{red}b \color{black}\left(a^{2}-a b+b^{2}\right)\) |
| Multiplicar. | \(a^{3}-a^{2} b+a b^{2}+a^{2} b-a b^{2}+b^{3}\) |
| Combina términos similares. | \(a^{3}+b^{3}\) |
\[a^3+b^3=(a+b)(a^2−ab+b^2\nonumber\]\[a^3−b^3=(a−b)(a^2+ab+b^2)\nonumber\]
Los dos patrones se ven muy similares, ¿no? Pero fíjense las señales en los factores. El signo del factor binomial coincide con el signo del binomio original. Y el signo del término medio del factor trinomio es lo opuesto al signo en el binomio original. Si reconoces el patrón de los signos, puede ayudarte a memorizar los patrones.

El factor trinomio en el patrón de suma y diferencia de cubos no se puede factorizar.
Será muy útil si aprendes a reconocer los cubos de los enteros del 1 al 10, igual que has aprendido a reconocer cuadrados. Hemos enumerado los cubos de los enteros del 1 al 10 en la Tabla.
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| \(n^3\) | 1 | 8 | 27 | 64 | 125 | 216 | 343 | 512 | 729 | 1000 |
Factor:\(x^3+64\).
- Responder
-





Factor:\(x^3+27\).
- Responder
-
\((x+3)(x^2−3x+9)\)
Factor:\(y^3+8\).
- Responder
-
\((y+2)(y^2−2y+4)\)
- ¿El binomio se ajusta al patrón de suma o diferencia de cubos?
¿Es una suma o diferencia?
¿Los primeros y últimos términos son los cubos perfectos? - Escríbelos como cubos.
- Utilice el patrón de suma o diferencia de cubos.
- Simplifica dentro de los paréntesis.
- Verificar multiplicando los factores.
Factor:\(27u^3−125v^3\).
- Responder
-
\(27 u^{3}-125 v^{3}\) Este binomio es una diferencia. El primer y último
término son cubos perfectos.Escribe los términos como cubos. 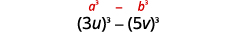
Usa la diferencia de patrón de cubos. 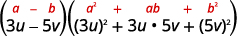
Simplificar. 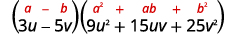
Verificar multiplicando. Te dejaremos el cheque a ti.
Factor:\(8x^3−27y^3\).
- Responder
-
\((2x−3y)(4x^2+6xy+9y^2)\)
Factor:\(1000m^3−125n^3\).
- Responder
-
\((10m−5n)(100m^2+50mn+25n^2)\)
En el siguiente ejemplo, primero factorizamos el GCF. Entonces podemos reconocer la suma de cubos.
Factor:\(6x^3y+48y^4\).
- Responder
-
\(6 x^{3} y+48 y^{4}\) Facturar el factor común. \(6 y\left(x^{3}+8 y^{3}\right)\) Este binomio es una suma Los
términos primero y último son cubos perfectos.Escribe los términos como cubos. 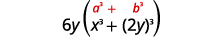
Usa el patrón de suma de cubos. 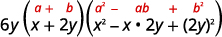
Simplificar. 
Comprobar:
Para verificar, puede resultarle más fácil multiplicar primero la suma de factores de cubos, luego multiplicar ese producto por 6y.6y. Te dejaremos la multiplicación.
Factor:\(500p^3+4q^3\).
- Responder
-
\(4(5p+q)(25p^2−5pq+q^2)\)
Factor:\(432c^3+686d^3\).
- Responder
-
\(2(6c+7d)(36c^2−42cd+49d^2)\)
El primer término en el siguiente ejemplo es un binomio en cubos.
Factor:\((x+5)^3−64x^3\).
- Responder
-
\((x+5)^{3}-64 x^{3}\) Este binomio es una diferencia. El primer y
último término son cubos perfectos.Escribe los términos como cubos. 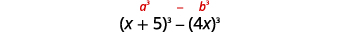
Usa la diferencia de patrón de cubos. 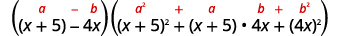
Simplificar. \((x+5-4 x)\left(x^{2}+10 x+25+4 x^{2}+20 x+16 x^{2}\right)\) \((-3 x+5)\left(21 x^{2}+30 x+25\right)\) Verificar multiplicando. Te dejaremos el cheque a ti.
Factor:\((y+1)^3−27y^3\).
- Responder
-
\((−2y+1)(13y^2+5y+1)\)
Factor:\((n+3)^3−125n^3\).
- Responder
-
\((−4n+3)(31n^2+21n+9)\)
Acceda a este recurso en línea para obtener instrucción adicional y práctica con productos especiales de factorización.
Conceptos clave
- Trinomios Cuadrados Perfectos Patrón: Si a y b son números reales,
\[\begin{array} {l} a^2+2ab+b^2=(a+b)^2 \\ a^2−2ab+b^2=(a−b)^2\end{array} \nonumber\]
- Cómo factorizar trinomios cuadrados perfectos.
\(\begin{array} {lllll} \textbf{Step 1.} &\text{Does the trinomial fit the pattern?} &\quad &\hspace{7mm} a^2+2ab+b^2 &\hspace{7mm} a^2−2ab+b^2 \\ &\text{Are the first and last terms perfect squares?} &\quad & &\\ &\text{Write them as squares.} &\quad &\hspace{5mm}(a)^2\hspace{16mm} (b)^2 &\hspace{6mm}(a)^2\hspace{16mm} (b)^2 \\ &\text{Check the middle term. Is it }2ab? &\quad &\hspace{12mm} {\,}^{\searrow}{\,}_{2·a·b}{\,}^{\swarrow} &\hspace{12mm} {\,}^{\searrow}{\,}_{2·a·b}{\,}^{\swarrow} \\ \textbf{Step 2.} &\text{Write the square of the binomial.} &\quad &\hspace{13mm} (a+b)^2 &\hspace{13mm} (a−b)^2 \\ \textbf{Step 3.} &\text{Check by multiplying.} & & & \end{array}\) - Diferencia de Cuadrados Patrón: Si a, ba, b son números reales,
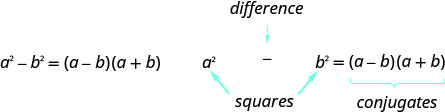
- Cómo factorizar las diferencias de cuadrados.
\(\begin{array} {llll} \textbf{Step 1.} &\text{Does the binomial fit the pattern?} &\qquad &\hspace{5mm} a^2−b^2 \\ &\text{Is this a difference?} &\qquad &\hspace{2mm} \text{____−____} \\ &\text{Are the first and last terms perfect squares?} & & \\ \textbf{Step 2.} &\text{Write them as squares.} &\qquad &\hspace{3mm} (a)^2−(b)^2 \\ \textbf{Step 3.} &\text{Write the product of conjugates.} &\qquad &(a−b)(a+b) \\ \textbf{Step 4.} &\text{Check by multiplying.} & & \end{array}\) - Patrón de suma y diferencia de cubos
\(\begin{array} {l} a^3+b3=(a+b)(a^2−ab+b^2) \\ a^3−b^3=(a−b)(a^2+ab+b^2) \end{array} \) - Cómo factorizar la suma o diferencia de cubos.
- ¿El binomio se ajusta al patrón de suma o diferencia de cubos?
¿Es una suma o diferencia?
¿Los primeros y últimos términos son los cubos perfectos? - Escríbelos como cubos.
- Utilice el patrón de suma o diferencia de cubos.
- Simplificar dentro de los paréntesis
- Verificar multiplicando los factores.
- ¿El binomio se ajusta al patrón de suma o diferencia de cubos?


