Saltar al contenido principal
LibreTexts Español

7.6E: Ejercicios

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    112722

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Resolver proporciones

    En los siguientes ejercicios, resuelve cada proporción.

    1. \(\dfrac{x}{56}=\dfrac{7}{8}\)

    Responder

    \(x=49\)

    2. \(\dfrac{56}{72}=\dfrac{y}{9}\)

    3. \(\dfrac{98}{154}=\dfrac{-7}{p}\)

    Responder

    \(p=-11\)

    4. \(\dfrac{72}{156}=\dfrac{-6}{q}\)

    5. \(\dfrac{a}{a+12}=\dfrac{4}{7}\)

    Responder

    \(a=16\)

    6. \(\dfrac{b}{b-16}=\dfrac{11}{9}\)

    7. \(\dfrac{m+90}{25}=\dfrac{m+30}{15}\)

    Responder

    \(m=60\)

    8. \(\dfrac{n+10}{4}=\dfrac{40-n}{6}\)

    9. \(\dfrac{2 p+4}{8}=\dfrac{p+18}{6}\)

    Responder

    \(p=30\)

    10. \(\dfrac{q-2}{2}=\dfrac{2 q-7}{18}\)

    En los siguientes ejercicios, resuelve.

    1. Kevin quiere mantener su ritmo cardíaco a 160 latidos por minuto mientras entrena. Durante su entrenamiento cuenta 27 latidos en 10 segundos.
      1. ¿Cuántos latidos por minuto es esto?
      2. ¿Kevin ha cumplido con su frecuencia cardíaca objetivo?
    Contestar
    1. 162 latidos por minuto
    2. si
    1. El auto de Jesse obtiene 30 millas por galón de gasolina.
      1. Si Las Vegas está a 285 millas de distancia, ¿cuántos galones de gasolina se necesitan para llegar y luego a casa?
      2. Si el gas es de $3.09 por galón, ¿cuál es el costo total del gas para el viaje?
    2. Los pediatras prescriben 5 mililitros (ml) de acetaminofén por cada 25 libras del peso de un niño. ¿Cuántos mililitros de acetaminofén le recetará el médico a Jocelyn, quien pesa 45 libras?
    Contestar

    9 ml

    1. Un veterinario le recetó a Sunny, un perro de 65 libras, un medicamento antibacteriano en caso de que surja una infección después de limpiarse los dientes. Si la dosis es de 5 mg por cada libra, ¿cuánto medicamento le dio Sunny?
    2. Una nueva bebida energética anuncia 106 calorías por 8 onzas. ¿Cuántas calorías hay en 12 onzas de la bebida?
    Contestar

    159 calorías

    1. Una lata de refresco de 12 onzas tiene 150 calorías. Si Josiah bebe el gran tamaño de 32 onzas del mini-mart local, ¿cuántas calorías obtiene?
    2. Kyra viaja a Canadá y cambiará 250 dólares estadounidenses a dólares canadienses. Al tipo de cambio actual, $1 US equivale a 1.3 dólares canadienses. ¿Cuántos dólares canadienses obtendrá por su viaje?
    Contestar

    325 Dolares Canadienses

    1. Maurice viaja a México y necesita cambiar 450 dólares por pesos mexicanos. Si cada dólar vale 12.29 pesos, ¿cuántos pesos obtendrá por su viaje?
    2. Ronald necesita una bebida matutina para el desayuno que le dé al menos 390 calorías. El jugo de naranja tiene 130 calorías en una taza. ¿Cuántas tazas necesita beber para alcanzar su meta calórica?
    Contestar

    3 tazas

    1. Sonya bebe una bebida energética de 32 onzas que contiene 80 calorías por 12 onza. ¿Cuántas calorías bebió?
    2. Phil quiere fertilizar su césped. Cada bolsa de fertilizante cubre alrededor de 4,000 pies cuadrados de césped. El césped de Phil es aproximadamente 13.500 pies cuadrados. ¿Cuántas bolsas de fertilizante tendrá que comprar?
    Contestar

    4 bolsas

    1. Una receta de galleta de avena requiere una\(\dfrac{1}{2}\) taza de mantequilla para hacer 4 docenas de galletas. Hilda necesita hacer 10 docenas de galletas para la venta de repostería. ¿Cuántas tazas de mantequilla necesitará?

    Resolver aplicaciones de figuras similares

    En los siguientes ejercicios, los triángulos son similares. Encuentra la longitud del lado indicado.

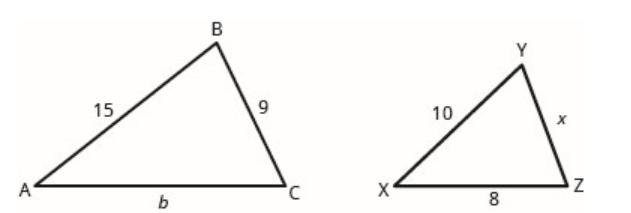
    clipboard_e2f4673192b7c1129ce5356edf37d371a.png

    1. lado x
    2. lado b
    Contestar
    1. 6
    2. 12

    clipboard_e6f2b994e4071945e8c679cdeca0a25e2.png

    1. lado d
    2. lado q

    En los siguientes ejercicios, utilice el mapa que se muestra. En el mapa, la ciudad de Nueva York, Chicago y Memphis forman un triángulo. La distancia real de Nueva York a Chicago es de 800 millas.

    clipboard_ea53c60f88204bada322018a4b3655dde.png

    1. Encuentra la distancia real de Nueva York a Memphis.
    Contestar

    950 millas

    1. Encuentra la distancia real de Chicago a Memphis.

    En los siguientes ejercicios, utilice el mapa que se muestra. En el mapa, Atlanta, Miami y Nueva Orleans forman un triángulo. La distancia real de Atlanta a Nueva Orleans es de 420 millas.

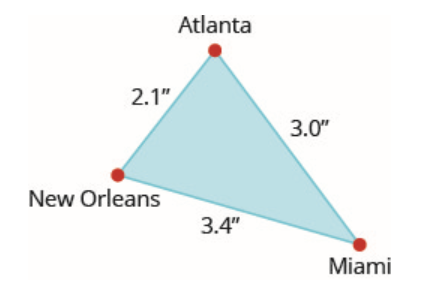
    clipboard_e35cfce340abef1ec8e033b58d4f2c3ae.png

    1. Encuentra la distancia real de Nueva Orleans a Miami.
    Contestar

    680 millas

    1. Encuentra la distancia real de Atlanta a Miami.

    En los siguientes ejercicios, responda a cada pregunta.

    1. Un perro de 2 pies de altura proyecta una sombra de 3 pies al mismo tiempo que un gato proyecta una sombra de un pie. ¿Qué tan alto es el gato?
    Contestar

    \(\dfrac{2}{3}\)pie (8 pulg.)

    1. Larry y Tom estaban parados uno al lado del otro en el patio trasero cuando Tom desafió a Larry a adivinar qué tan alto era. Larry sabía que su propia estatura es de 6.5 pies y cuando midieron sus sombras, la sombra de Larry era de 8 pies y la de Tom tenía 7.75 pies de largo. ¿Cuál es la altura de Tom?
    2. La porción de torre de un molino de viento mide 212 pies de altura. Una persona de seis pies de altura parada junto a la torre proyecta una sombra de siete pies. ¿Cuánto dura la sombra del molino?
    Contestar

    247.3 pies

    1. La altura de la Estatua de la Libertad es de 305 pies. Nikia, que está parada junto a la estatua, proyecta una sombra de 6 pies y mide 5 pies de altura. ¿Cuánto tiempo debe durar la sombra de la estatua?

    Resolver aplicaciones de movimiento uniforme

    En los siguientes ejercicios, resolver el problema de aplicación proporcionado.

    1. Mary realiza un recorrido turístico en un helicóptero que puede volar 450 millas contra un viento en contra de 35 mph en la misma cantidad de tiempo que puede viajar 702 millas con un viento de cola de 35 mph. Encuentra la velocidad del helicóptero.
    Contestar

    160 mph

    1. Un jet privado puede volar 1,210 millas contra un viento en contra de 25 mph en la misma cantidad de tiempo que puede volar 1694 millas con un viento de cola de 25 mph. Encuentra la velocidad del jet.
    2. Un barco viaja 140 millas río abajo al mismo tiempo que viaja 92 millas río arriba. La velocidad de la corriente es de 6mph. ¿Cuál es la velocidad de la embarcación?
    Contestar

    29 mph

    1. Darrin puede andar en patineta 2 millas contra un viento de 4 mph en la misma cantidad de tiempo que patina 6 millas con un viento de 4 mph. Encuentra las patinetas Darrin de velocidad sin viento.
    2. Jane pasó 2 horas explorando una montaña con una moto de cross. Primero, ella montó 40 millas cuesta arriba. Después de llegar a la cima, cabalgó 12 millas a lo largo de la cumbre. Mientras iba cuesta arriba, fue 5 mph más lenta que cuando estaba en la cima. ¿Cuál era su ritmo a lo largo de la cumbre?
    Contestar

    30 mph

    1. Laney quería perder algo de peso así que planeó un día de ejercicio. Pasó un total de 2 horas montando su bicicleta y trotando. Ella viajó en bicicleta por 12 millas y trotó por 6 millas. Su tarifa para trotar era de 10 mph menos que la tasa de ciclismo. ¿Cuál era su tarifa al trotar?
    2. Byron quería probar diferentes embarcaciones acuáticas. Se fue 62 millas río abajo en una lancha a motor y 27 millas río abajo en una moto acuática. Su velocidad en la moto acuática era 10 mph más rápida que en la lancha motora. Bill pasó un total de 4 horas en el agua. ¿Cuál era su tasa de velocidad en la lancha motora?
    Responder

    20 mph

    1. Nancy tomó un viaje de 3 horas. Se fue 50 millas antes de quedar atrapada en una tormenta. Entonces manejó 68 millas a 9 mph menos de lo que había conducido cuando hacía buen tiempo. ¿Cuál era su velocidad conduciendo en la tormenta?
    2. Chester montó su bicicleta cuesta arriba 24 millas y luego regresó cuesta abajo a 2 mph más rápido que su cuesta arriba. Si le tomó 2 horas más andar cuesta arriba que cuesta abajo, ¿cuál era su tarifa cuesta arriba?
    Responder

    4 mph

    1. Matthew corrió a la casa de su amigo a 12 millas de distancia y luego se llevó de regreso a casa. Le tomó 2 horas más trotar ahí que regresar. Su tasa de trote era 25 mph más lenta que la velocidad cuando estaba montando. ¿Cuál era su tasa de jogging?
    2. Hudson recorre 1080 millas en un jet y luego 240 millas en automóvil para llegar a una reunión de negocios. El jet va 300 mph más rápido que la velocidad del automóvil, y el viaje en automóvil dura 1 hora más que el jet. ¿Cuál es la velocidad del auto?
    Responder

    60 mph

    1. Nathan caminó por una vía asfáltica por 12 millas. Caminó las 12 millas de regreso a su auto en un camino de grava a través del bosque. Sobre el asfalto caminó 2 millas por hora más rápido que sobre la grava. El paseo sobre la grava tardó una hora más que el paseo sobre el asfalto. ¿Qué tan rápido caminó sobre la grava?
    2. John puede volar su avión 2800 millas con una velocidad del viento de 50 mph al mismo tiempo que puede viajar 2400 millas contra el viento. Si la velocidad del viento es de 50 mph, encuentra la velocidad de su avión.
    Responder

    650 mph

    1. La lancha rápida de Jim puede viajar 20 millas río arriba contra una corriente de 3 mph en la misma cantidad de tiempo que viaja 22 millas aguas abajo con una velocidad actual de 3 mph. Encuentra la velocidad del bote Jim.
    2. Hazel necesita llegar a la casa de su nieta tomando un avión y un auto de alquiler. Viaja 900 millas en avión y 250 millas en auto. El avión viaja 250 mph más rápido que el auto. Si conduce el auto de alquiler por 2 horas más de lo que viajó en el avión, encuentre la velocidad del auto.
    Responder

    50 mph

    1. Stu entrenó durante 3 horas ayer. Corrió 14 millas y luego viajó en bicicleta 40 millas. Su velocidad de ciclismo es 6 mph más rápida que su velocidad de carrera. ¿Cuál es su velocidad de carrera?
    2. Al conducir el viaje de 9 horas a casa, Sharon condujo 390 millas en la interestatal y 150 millas en carreteras rurales. Su velocidad en la interestatal era 15 más que en las carreteras rurales. ¿Cuál era su velocidad en las carreteras rurales?
    Responder

    50 mph

    1. A dos hermanas les gusta competir en sus paseos en bicicleta. Tamara puede ir 4 mph más rápido que su hermana, Samantha. Si Samantha tarda 1 hora más que Tamara en recorrer 80 millas, ¿qué tan rápido puede Samantha andar en bicicleta?
    2. A Dana le gusta llevar a su perro a pasear, pero a veces su perro se escapa, y tiene que correr tras él. Dana caminó a su perro por 7 millas pero luego tuvo que correr 1 milla, pasando un tiempo total de 2.5 horas con su perro. Su velocidad de carrera era 3 mph más rápida que su velocidad de caminar. Encuentra su velocidad de caminar.
    Responder

    4.2 mph

    1. Ken y Joe salen de su departamento para ir a un partido de fútbol a 45 millas de distancia. Ken conduce su auto 30 mph más rápido Joe puede andar en bicicleta. Si Joe tarda 2 horas más que Ken en llegar al juego, ¿cuál es la velocidad de Joe?

    Resolver aplicaciones de trabajo

    1. Mike, un albañil experimentado, puede construir una pared en 3 horas, mientras que su hijo, que está aprendiendo, puede hacer el trabajo en 6 horas. ¿Cuánto tiempo les toma construir un muro juntos?
    Responder

    2 horas

    1. Sam tarda 4 horas en rastrillar el césped delantero mientras su hermano, Dave, puede rastrillar el césped en 2 horas. ¿Cuánto tiempo les llevará rastrillar el césped trabajando juntos?
    2. Mia puede limpiar su departamento en 6 horas mientras que su compañera de cuarto puede limpiar el departamento en 5 horas. Si trabajan juntos, ¿cuánto tiempo les llevaría limpiar el departamento?
    Responder

    2 horas y 44 minutos

    1. Brian puede colocar una losa de concreto en 6 horas, mientras que Greg puede hacerlo en 4 horas. Si Brian y Greg trabajan juntos, ¿cuánto tiempo tomará?
    2. Josephine puede corregir los papeles de prueba de sus alumnos en 5 horas, pero si la asistente de su maestra ayuda, les tomaría 3 horas. ¿Cuánto tiempo tardaría el asistente en hacerlo solo?
    Responder

    7 horas y 30 minutos

    1. Lavando el auto de su papá solo, Levi de ocho años tarda 2.5 horas y medio. Si su papá le ayuda, entonces toma 1 hora. ¿Cuánto tiempo le toma al papá de Levi's lavar el auto solo?
    2. Al final del día Dodie puede limpiar su peluquería en 15 minutos. Ann, que trabaja con ella, puede limpiar el salón en 30 minutos. ¿Cuánto tiempo les llevaría limpiar la tienda si trabajan juntos?
    Responder

    10 min

    1. Ronald puede palear el camino de entrada en 4 horas, pero si su hermano Donald ayuda tardaría 2 horas. ¿Cuánto tiempo le tomaría a Donald palear el camino de entrada solo?

    Resolver problemas de variación directa

    En los siguientes ejercicios, resuelve.

    1. Si\(y\) varía directamente a medida\(x\) y\(y=14\), cuándo\(x=3\). Encuentra la ecuación que relaciona\(x\) y\(y\).
    Responder

    \(y=\dfrac{14}{3} x\)

    1. Si\(a\) varía directamente a medida\(b\) y\(a=16\), cuándo\(b=4\). Encuentra la ecuación que relaciona\(a\) y\(b\).
    2. Si\(p\) varía directamente a medida\(q\) y\(p=9\), cuándo\(q=3\). Encuentra la ecuación que relaciona\(p\) y\(q\).
    Responder

    \(p=3.2 q\)

    1. Si\(v\) varía directamente a medida\(w\) y\(v=8\), cuándo\(w=12\). Encuentra la ecuación que relaciona\(v\) y\(w\).
    2. El precio,\(P\), que Eric paga por la gasolina varía directamente con el número de galones\(g\),, compra. Le cuesta 50 dólares comprar 20 galones de gas.
      1. Escribe la ecuación que relaciona\(P\) y\(g\).
      2. ¿Cuánto le costarían 33 galones a Eric?
    Responder
    1. \(P=2.5 g\)
    2. \(\$ 82.50\)
    1. Joseph está viajando en un viaje por carretera. La distancia,\(d\), recorre antes de detenerse a almorzar varía directamente con la velocidad,\(v\), recorre. Puede recorrer 120 millas a una velocidad de 60 mph.
      1. Escribe la ecuación que relaciona\(d\) y\(v\).
      2. ¿Hasta dónde viajaría antes de detenerse a almorzar a una velocidad de 65 mph?
    2. La masa de un líquido varía directamente con su volumen. Un líquido con masa 16 kilogramos tiene un volumen de 2 litros.
      1. Escribe la ecuación que relaciona la masa con el volumen.
      2. ¿Cuál es el volumen de este líquido si su masa es de 128 kilogramos?
    Responder
    1. \(m=8 v\)
    2. 16 litros
    1. La longitud que estira un resorte varía directamente con un peso colocado al final del resorte. Cuando Sarah colocó una sandía de 10 libras en una báscula colgante, el resorte se estiró 5 pulgadas.
      1. Escribe la ecuación que relaciona la longitud del resorte con el peso.
      2. ¿Qué peso de la sandía estiraría la primavera 6 pulgadas?
    2. La carga máxima que soportará una viga varía directamente con el cuadrado de la diagonal de la sección transversal de la viga. Una viga con diagonal de 6 pulgadas soportará una carga máxima de 108 libras.
      1. Escribe la ecuación que relaciona la carga con la diagonal de la sección transversal.
      2. ¿Qué carga soportará una viga con una diagonal de 10 pulgadas?
    Responder
    1. \(L=3 d^{2}\)
    2. 300 libras
    1. El área de un círculo varía directamente como el cuadrado del radio. Una pizza circular con un radio de 6 pulgadas tiene un área de 113.04 pulgadas cuadradas.
      1. Escribe la ecuación que relaciona el área con el radio.
      2. ¿Cuál es el área de una pizza personal con un radio de 4 pulgadas?

    Resolver problemas de variación inversa

    En los siguientes ejercicios, resuelve.

    1. I f\(y\) varía inversamente con\(x\) and \(y=5\), when \(x=4\). F ind la ecuación que relaciona\(x\) y\(y\).
    Responder

    \(y=\dfrac{20}{x}\)

    1. I f\(p\) varía inversamente con\(q\) and \(p=2\), when \(q=1\). F ind la ecuación que relaciona\(p\) y\(q\).
    2. I f\(v\) varía inversamente con\(w\) and \(v=6\), when \(w=12\). F ind la ecuación que relaciona\(v\) y\(w\).
    Responder

    \(v=\dfrac{3}{w}\)

    1. I f\(a\) varía inversamente con\(b\) and \(a=12\), when \(b=13\). F ind la ecuación que relaciona\(a\) y\(b\).

    En los siguientes ejercicios, escribe una ecuación de variación inversa para resolver los siguientes problemas.

    1. El consumo de combustible (mpg) de un automóvil varía inversamente con su peso. Un Toyota Corolla pesa 2800 libras consiguiendo 33 mpg en la carretera.
      1. Escribe la ecuación que relaciona el mpg con el peso del auto.
      2. ¿Cuál sería el consumo de combustible para un Toyota Sequoia que pesa 5500 libras?
    Responder
    1. \(g=\dfrac{92,400}{w}\)
    2. 16.8 mpg
    1. El valor de un automóvil varía inversamente con su antigüedad. Jackie compró un auto de 10 años por $2,400.
      1. Escribe la ecuación que relaciona el valor del auto con su antigüedad.
      2. ¿Cuál será el valor del auto de Jackie cuando tenga 15 años?
    2. El tiempo requerido para vaciar un tanque varía inversamente según la velocidad de bombeo. Ada tardó 5 horas en bombear su sótano inundado usando una bomba que tenía una calificación de 200 gpm (galones por minuto).
      1. Escribe la ecuación que relaciona el número de horas con la velocidad de bombeo.
      2. ¿Cuánto tiempo le tomaría a Ada bombear su sótano si usara una bomba con una calificación de 400 gpm?
    Responder
    1. \(t=\dfrac{1000}{r}\)
    2. 2.5 horas
    1. En un instrumento de cuerda, la longitud de una cuerda varía inversamente a medida que la frecuencia de sus vibraciones. Una cuerda de 11 pulgadas en un violín tiene una frecuencia de 400 ciclos por segundo.
      1. Escribe la ecuación que relaciona la longitud de la cadena con su frecuencia.
      2. ¿Cuál es la frecuencia de una cuerda de 10 pulgadas?
    2. Paul, un dentista, determinó que el número de caries que se desarrollan en la boca de su paciente cada año varía inversamente al número de minutos que pasa cepillarse cada noche. Su paciente, Lori, presentaba cuatro caries al cepillarse los dientes 30 segundos (0.5 minutos) cada noche.
      1. Escribe la ecuación que relaciona el número de cavidades con el tiempo dedicado al cepillado.
      2. ¿Cuántas caries esperaría Paul que tuviera Lori si se hubiera cepillado los dientes durante 2 minutos cada noche?
    Responder
    1. \(c=\dfrac{2}{t}\)
    2. 1 cavidad
    1. La ley de Boyle establece que si la temperatura de un gas se mantiene constante, entonces la presión varía inversamente al volumen del gas. Braydon, un buceador, tiene un tanque que contiene 6 litros de aire bajo una presión de 220 psi.
      1. Escribe la ecuación que relaciona la presión con el volumen.
      2. Si la presión aumenta a 330 psi, ¿cuánto aire puede contener el tanque de Braydon?
    2. El costo de un servicio de viaje varía directamente con la distancia recorrida. Cuesta $35 por un viaje desde el centro de la ciudad hasta el aeropuerto, a 14 millas de distancia.
      1. Escribe la ecuación que relaciona el costo,\(c\), con el número de millas,\(m\).
      2. ¿Cuánto costaría viajar 22 millas con este servicio?
    Responder
    1. \(c=2.5 m\)
    2. \(\$ 55\)
    1. El número de horas que tarda Jack en conducir de Boston a Bangor es inversamente proporcional a su velocidad promedio de conducción. Cuando conduce a una velocidad promedio de 40 millas por hora, le toma 6 horas para el viaje.
      1. Escribe la ecuación que relaciona el número de horas,\(h\), con la velocidad,\(s\).
      2. ¿Cuánto tardaría el viaje si su velocidad promedio fuera de 75 millas por hora?

    Ejercicios de escritura

    1. Marisol resuelve la proporción\(\dfrac{144}{a}=\dfrac{9}{4}\) por 'multiplicación cruzada', por lo que su primer paso parece\(4 \cdot 144=9 \cdot a\).Explique en qué se diferencia esto del método de solución mostrado en el Ejemplo 7.6.2.
    Responder

    Las respuestas variarán.

    1. Paula y Yuki son compañeras de cuarto. Paula tarda 3 horas en limpiar su departamento. Yuki tarda 4 horas en limpiar el departamento. La ecuación se\(\dfrac{1}{3}+\dfrac{1}{4}=\dfrac{1}{t}\) puede utilizar para encontrar\(t\), el número de horas que tomaría a ambos, trabajando juntos, para limpiar su departamento. Explique cómo esta ecuación modela la situación.
    2. En sus propias palabras, explique la diferencia entre la variación directa y la variación inversa.
    Responder

    Las respuestas variarán.

    1. Haz un ejemplo a partir de tu experiencia de vida de variación inversa.

    This page titled 7.6E: Ejercicios is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by OpenStax via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.