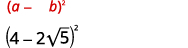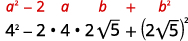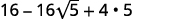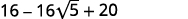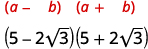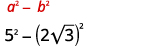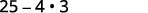Saltar al contenido principal
LibreTexts Español

8.5: Sumar, restar y multiplicar expresiones radicales

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    112540

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de aprendizaje

    Al final de esta sección, podrás:

    • Sumar y restar expresiones radicales
    • Multiplicar expresiones radicales
    • Usar multiplicación polinómica para multiplicar expresiones radicales

    Antes de comenzar, toma este cuestionario de preparación.

    1. Agregar:\(3x^{2}+9x−5−(x^{2}−2x+3)\).
      Si te perdiste este problema, revisa el Ejemplo 5.5.
    2. Simplificar:\((2+a)(4−a)\).
      Si te perdiste este problema, revisa el Ejemplo 5.28.
    3. Simplificar:\((9−5y)^{2}\).
      Si te perdiste este problema, revisa el Ejemplo 5.31.

    Sumar y restar expresiones radicales

    Agregar expresiones radicales con el mismo índice y el mismo radicando es como agregar términos similares. Llamamos radicales con el mismo índice y el mismo radicando como radicales para recordarnos que funcionan igual que términos similares.

    Definición\(\PageIndex{1}\): Like Radicals

    Como radicales son expresiones radicales con el mismo índice y el mismo radicando.

    Sumamos y restamos como radicales de la misma manera que sumamos y restamos términos similares. Sabemos que\(3x+8x\) es\(11x\) .Del mismo modo agregamos\(3 \sqrt{x}+8 \sqrt{x}\) y el resultado es\(11 \sqrt{x}\).

    Piense en agregar términos similares con variables como lo hace en los siguientes ejemplos. Cuando tienes como radicales, simplemente sumas o restas los coeficientes. Cuando los radicales no son como, no se pueden combinar los términos.

    Ejemplo\(\PageIndex{1}\)

    Simplificar:

    1. \(2 \sqrt{2}-7 \sqrt{2}\)
    2. \(5 \sqrt[3]{y}+4 \sqrt[3]{y}\)
    3. \(7 \sqrt[4]{x}-2 \sqrt[4]{y}\)

    Solución:

    a.

    \(2 \sqrt{2}-7 \sqrt{2}\)

    Como los radicales son como, restamos los coeficientes.

    \(-5 \sqrt{2}\)

    b.

    \(5 \sqrt[3]{y}+4 \sqrt[3]{y}\)

    Ya que los radicales son como, sumamos los coeficientes.

    \(9 \sqrt[3]{y}\)

    c.

    \(7 \sqrt[4]{x}-2 \sqrt[4]{y}\)

    Los índices son los mismos pero los radicales son diferentes. Estos no son como radicales. Como los radicales no son como, no podemos restarlos.

    Ejercicio\(\PageIndex{1}\)

    Simplificar:

    1. \(8 \sqrt{2}-9 \sqrt{2}\)
    2. \(4 \sqrt[3]{x}+7 \sqrt[3]{x}\)
    3. \(3 \sqrt[4]{x}-5 \sqrt[4]{y}\)
    Contestar
    1. \(-\sqrt{2}\)
    2. \(11 \sqrt[3]{x}\)
    3. \(3 \sqrt[4]{x}-5 \sqrt[4]{y}\)
    Ejercicio\(\PageIndex{2}\)

    Simplificar:

    1. \(5 \sqrt{3}-9 \sqrt{3}\)
    2. \(5 \sqrt[3]{y}+3 \sqrt[3]{y}\)
    3. \(5 \sqrt[4]{m}-2 \sqrt[3]{m}\)
    Contestar
    1. \(-4 \sqrt{3}\)
    2. \(8 \sqrt[3]{y}\)
    3. \(5 \sqrt[4]{m}-2 \sqrt[3]{m}\)

    Para que los radicales sean como, deben tener el mismo índice y radicando. Cuando los radicandos contienen más de una variable, siempre y cuando todas las variables y sus exponentes sean idénticos, los radicandos son los mismos.

    Ejemplo\(\PageIndex{2}\)

    Simplificar:

    1. \(2 \sqrt{5 n}-6 \sqrt{5 n}+4 \sqrt{5 n}\)
    2. \(\sqrt[4]{3 x y}+5 \sqrt[4]{3 x y}-4 \sqrt[4]{3 x y}\)

    Solución:

    a.

    \(2 \sqrt{5 n}-6 \sqrt{5 n}+4 \sqrt{5 n}\)

    Ya que los radicales son como, los combinamos.

    \(0 \sqrt{5 n}\)

    Simplificar.

    \(0\)

    b.

    \(\sqrt[4]{3 x y}+5 \sqrt[4]{3 x y}-4 \sqrt[4]{3 x y}\)

    Ya que los radicales son como, los combinamos.

    \(2 \sqrt[4]{3 x y}\)

    Ejercicio\(\PageIndex{3}\)

    Simplificar:

    1. \(\sqrt{7 x}-7 \sqrt{7 x}+4 \sqrt{7 x}\)
    2. \(4 \sqrt[4]{5 x y}+2 \sqrt[4]{5 x y}-7 \sqrt[4]{5 x y}\)
    Contestar
    1. \(-2 \sqrt{7 x}\)
    2. \(-\sqrt[4]{5 x y}\)
    Ejercicio\(\PageIndex{4}\)

    Simplificar:

    1. \(4 \sqrt{3 y}-7 \sqrt{3 y}+2 \sqrt{3 y}\)
    2. \(6 \sqrt[3]{7 m n}+\sqrt[3]{7 m n}-4 \sqrt[3]{7 m n}\)
    Contestar
    1. \(-\sqrt{3 y}\)
    2. \(3 \sqrt[3]{7 m n}\)

    Recuerda que siempre simplificamos los radicales al eliminar el factor más grande del radicando que es una potencia del índice. Una vez que se simplifica cada radical, entonces podemos decidir si son como radicales.

    Ejemplo\(\PageIndex{3}\)

    Simplificar:

    1. \(\sqrt{20}+3 \sqrt{5}\)
    2. \(\sqrt[3]{24}-\sqrt[3]{375}\)
    3. \(\frac{1}{2} \sqrt[4]{48}-\frac{2}{3} \sqrt[4]{243}\)

    Solución:

    a.

    \(\sqrt{20}+3 \sqrt{5}\)

    Simplifica los radicales, cuando sea posible.

    \(\sqrt{4} \cdot \sqrt{5}+3 \sqrt{5}\)

    \(2 \sqrt{5}+3 \sqrt{5}\)

    Combina los radicales similares.

    \(5 \sqrt{5}\)

    b.

    \(\sqrt[3]{24}-\sqrt[3]{375}\)

    Simplifica los radicales.

    \(\sqrt[3]{8} \cdot \sqrt[3]{3}-\sqrt[3]{125} \cdot \sqrt[3]{3}\)

    \(2 \sqrt[3]{3}-5 \sqrt[3]{3}\)

    Combina los radicales similares.

    \(-3 \sqrt[3]{3}\)

    c.

    \(\frac{1}{2} \sqrt[4]{48}-\frac{2}{3} \sqrt[4]{243}\)

    Simplifica los radicales.

    \(\frac{1}{2} \sqrt[4]{16} \cdot \sqrt[4]{3}-\frac{2}{3} \sqrt[4]{81} \cdot \sqrt[4]{3}\)

    \(\frac{1}{2} \cdot 2 \cdot \sqrt[4]{3}-\frac{2}{3} \cdot 3 \cdot \sqrt[4]{3}\)

    \(\sqrt[4]{3}-2 \sqrt[4]{3}\)

    Combina los radicales similares.

    \(-\sqrt[4]{3}\)

    Ejercicio\(\PageIndex{5}\)

    Simplificar:

    1. \(\sqrt{18}+6 \sqrt{2}\)
    2. \(6 \sqrt[3]{16}-2 \sqrt[3]{250}\)
    3. \(\frac{2}{3} \sqrt[3]{81}-\frac{1}{2} \sqrt[3]{24}\)
    Contestar
    1. \(9 \sqrt{2}\)
    2. \(2 \sqrt[3]{2}\)
    3. \(\sqrt[3]{3}\)
    Ejercicio\(\PageIndex{6}\)

    Simplificar:

    1. \(\sqrt{27}+4 \sqrt{3}\)
    2. \(4 \sqrt[3]{5}-7 \sqrt[3]{40}\)
    3. \(\frac{1}{2} \sqrt[3]{128}-\frac{5}{3} \sqrt[3]{54}\)
    Contestar
    1. \(7 \sqrt{3}\)
    2. \(-10 \sqrt[3]{5}\)
    3. \(-3 \sqrt[3]{2}\)

    En el siguiente ejemplo, eliminaremos tanto los factores constantes como variables de los radicales. Ahora que hemos practicado tomando tanto las raíces pares como las impares de las variables, es una práctica común en este punto que supongamos que todas las variables son mayores o iguales a cero para que no se necesiten valores absolutos. Utilizaremos esta suposición a lo largo del resto de este capítulo.

    Ejemplo\(\PageIndex{4}\)

    Simplificar:

    1. \(9 \sqrt{50 m^{2}}-6 \sqrt{48 m^{2}}\)
    2. \(\sqrt[3]{54 n^{5}}-\sqrt[3]{16 n^{5}}\)

    Solución:

    a.

    \(9 \sqrt{50 m^{2}}-6 \sqrt{48 m^{2}}\)

    Simplifica los radicales.

    \(9 \sqrt{25 m^{2}} \cdot \sqrt{2}-6 \sqrt{16 m^{2}} \cdot \sqrt{3}\)

    \(9 \cdot 5 m \cdot \sqrt{2}-6 \cdot 4 m \cdot \sqrt{3}\)

    \(45 m \sqrt{2}-24 m \sqrt{3}\)

    Los radicales no son como y así no se pueden combinar.

    b.

    \(\sqrt[3]{54 n^{5}}-\sqrt[3]{16 n^{5}}\)

    Simplifica los radicales.

    \(\sqrt[3]{27 n^{3}} \cdot \sqrt[3]{2 n^{2}}-\sqrt[3]{8 n^{3}} \cdot \sqrt[3]{2 n^{2}}\)

    \(3 n \sqrt[3]{2 n^{2}}-2 n \sqrt[3]{2 n^{2}}\)

    Combina los radicales similares.

    \(n \sqrt[3]{2 n^{2}}\)

    Ejercicio\(\PageIndex{7}\)

    Simplificar:

    1. \(\sqrt{32 m^{7}}-\sqrt{50 m^{7}}\)
    2. \(\sqrt[3]{135 x^{7}}-\sqrt[3]{40 x^{7}}\)
    Contestar
    1. \(-m^{3} \sqrt{2 m}\)
    2. \(x^{2} \sqrt[3]{5 x}\)
    Ejercicio\(\PageIndex{8}\)

    Simplificar:

    1. \(\sqrt{27 p^{3}}-\sqrt{48 p^{3}}\)
    2. \(\sqrt[3]{256 y^{5}}-\sqrt[3]{32 n^{5}}\)
    Contestar
    1. \(-p \sqrt{3 p}\)
    2. \(4 y \sqrt[3]{4 y^{2}}-2 n \sqrt[3]{4 n^{2}}\)

    Multiplicar expresiones radicales

    Hemos utilizado la Propiedad del Producto de Raíces para simplificar las raíces cuadradas eliminando los factores cuadrados perfectos. Podemos utilizar la Propiedad Producto de Raíces 'a la reversa' para multiplicar raíces cuadradas. Recuerde, suponemos que todas las variables son mayores o iguales a cero.

    Reescribiremos la Propiedad del Producto de Raíces para que veamos ambos caminos juntos.

    Definición\(\PageIndex{2}\): Product Property of Roots

    Para cualquier número real,\(\sqrt[n]{a}\) y\(\sqrt[b]{n}\), y para cualquier número entero\(n≥2\)

    \(\sqrt[n]{a b}=\sqrt[n]{a} \cdot \sqrt[n]{b} \quad \text { and } \quad \sqrt[n]{a} \cdot \sqrt[n]{b}=\sqrt[n]{a b}\)

    Cuando multiplicamos dos radicales deben tener el mismo índice. Una vez multiplicamos los radicales, entonces buscamos factores que sean una potencia del índice y simplificamos al radical siempre que sea posible.

    Multiplicar radicales con coeficientes es muy parecido a multiplicar variables con coeficientes. Para multiplicar\(4x⋅3y\) multiplicamos los coeficientes juntos y luego las variables. El resultado es\(12xy\). Ten esto en cuenta al hacer estos ejemplos.

    Ejemplo\(\PageIndex{5}\)

    Simplificar:

    1. \((6 \sqrt{2})(3 \sqrt{10})\)
    2. \((-5 \sqrt[3]{4})(-4 \sqrt[3]{6})\)

    Solución:

    a.

    \((6 \sqrt{2})(3 \sqrt{10})\)

    Multiplicar usando la Propiedad del Producto.

    \(18\sqrt{20}\)

    Simplifica lo radical.

    \(18 \sqrt{4} \cdot \sqrt{5}\)

    Simplificar.

    \(18 \cdot 2 \cdot \sqrt{5}\)

    \(36 \sqrt{5}\)

    b.

    \((-5 \sqrt[3]{4})(-4 \sqrt[3]{6})\)

    Multiplicar usando la Propiedad del Producto.

    \(20 \sqrt[3]{24}\)

    Simplifica lo radical.

    \(20 \sqrt[3]{8} \cdot \sqrt[3]{3}\)

    Simplificar.

    \(20 \cdot 2 \cdot \sqrt[3]{3}\)

    \(40 \sqrt[3]{3}\)

    Ejercicio\(\PageIndex{9}\)

    Simplificar:

    1. \((3 \sqrt{2})(2 \sqrt{30})\)
    2. \((2 \sqrt[3]{18})(-3 \sqrt[3]{6})\)
    Contestar
    1. \(12 \sqrt{15}\)
    2. \(-18 \sqrt[3]{2}\)
    Ejercicio\(\PageIndex{10}\)

    Simplificar:

    1. \((3 \sqrt{3})(3 \sqrt{6})\)
    2. \((-4 \sqrt[3]{9})(3 \sqrt[3]{6})\)
    Contestar
    1. \(27 \sqrt{2}\)
    2. \(-36 \sqrt[3]{2}\)

    Seguimos los mismos procedimientos cuando hay variables en los radicandos.

    Ejemplo\(\PageIndex{6}\)

    Simplificar:

    1. \(\left(10 \sqrt{6 p^{3}}\right)(4 \sqrt{3 p})\)
    2. \(\left(2 \sqrt[4]{20 y^{2}}\right)\left(3 \sqrt[4]{28 y^{3}}\right)\)

    Solución:

    a.

    \(\left(10 \sqrt{6 p^{3}}\right)(4 \sqrt{3 p})\)

    Multiplicar.

    \(40 \sqrt{18 p^{4}}\)

    Simplifica lo radical.

    \(40 \sqrt{9 p^{4}} \cdot \sqrt{2}\)

    Simplificar.

    \(40 \cdot 3 p^{2} \cdot \sqrt{3}\)

    \(120 p^{2} \sqrt{3}\)

    b. Cuando los radicandos involucran grandes números, a menudo es ventajoso faccionarlos para encontrar los poderes perfectos.

    \(\left(2 \sqrt[4]{20 y^{2}}\right)\left(3 \sqrt[4]{28 y^{3}}\right)\)

    Multiplicar.

    \(6 \sqrt[4]{4 \cdot 5 \cdot 4 \cdot 7 y^{5}}\)

    Simplifica lo radical.

    \(6 \sqrt[4]{16 y^{4}} \cdot \sqrt[4]{35 y}\)

    Simplificar.

    \(6 \cdot 2 y \sqrt[4]{35 y}\)

    Multiplicar.

    \(12 y \sqrt[4]{35 y}\)

    Ejercicio\(\PageIndex{11}\)

    Simplificar:

    1. \(\left(6 \sqrt{6 x^{2}}\right)\left(8 \sqrt{30 x^{4}}\right)\)
    2. \(\left(-4 \sqrt[4]{12 y^{3}}\right)\left(-\sqrt[4]{8 y^{3}}\right)\)
    Contestar
    1. \(36 x^{3} \sqrt{5}\)
    2. \(8 y \sqrt[4]{3 y^{2}}\)
    Ejercicio\(\PageIndex{12}\)

    Simplificar:

    1. \(\left(2 \sqrt{6 y^{4}}\right)(12 \sqrt{30 y})\)
    2. \(\left(-4 \sqrt[4]{9 a^{3}}\right)\left(3 \sqrt[4]{27 a^{2}}\right)\)
    Contestar
    1. \(144 y^{2} \sqrt{5 y}\)
    2. \(-36 \sqrt[4]{3 a}\)

    Usar multiplicación polinomial para multiplicar expresiones radicales

    En los siguientes algunos ejemplos, usaremos la Propiedad Distributiva para multiplicar expresiones con radicales. Primero distribuiremos y luego simplificaremos los radicales cuando sea posible.

    Ejemplo\(\PageIndex{7}\)

    Simplificar:

    1. \(\sqrt{6}(\sqrt{2}+\sqrt{18})\)
    2. \(\sqrt[3]{9}(5-\sqrt[3]{18})\)

    Solución:

    a.

    \(\sqrt{6}(\sqrt{2}+\sqrt{18})\)

    Multiplicar.

    \(\sqrt{12}+\sqrt{108}\)

    Simplificar.

    \(\sqrt{4} \cdot \sqrt{3}+\sqrt{36} \cdot \sqrt{3}\)

    Simplificar.

    \(2 \sqrt{3}+6 \sqrt{3}\)

    Combina como radicales.

    \(8\sqrt{3}\)

    b.

    \(\sqrt[3]{9}(5-\sqrt[3]{18})\)

    Distribuir.

    \(5 \sqrt[3]{9}-\sqrt[3]{162}\)

    Simplificar.

    \(5 \sqrt[3]{9}-\sqrt[3]{27} \cdot \sqrt[3]{6}\)

    Simplificar.

    \(5 \sqrt[3]{9}-3 \sqrt[3]{6}\)

    Ejercicio\(\PageIndex{13}\)

    Simplificar:

    1. \(\sqrt{6}(1+3 \sqrt{6})\)
    2. \(\sqrt[3]{4}(-2-\sqrt[3]{6})\)
    Contestar
    1. \(18+\sqrt{6}\)
    2. \(-2 \sqrt[3]{4}-2 \sqrt[3]{3}\)
    Ejercicio\(\PageIndex{14}\)

    Simplificar:

    1. \(\sqrt{8}(2-5 \sqrt{8})\)
    2. \(\sqrt[3]{3}(-\sqrt[3]{9}-\sqrt[3]{6})\)
    Contestar
    1. \(-40+4 \sqrt{2}\)
    2. \(-3-\sqrt[3]{18}\)

    Cuando trabajamos con polinomios, multiplicamos binomios por binomios. Recuerda, esto nos dio cuatro productos antes de combinar cualquier término similar. Para asegurarnos de obtener los cuatro productos, organizamos nuestro trabajo, generalmente por el método FOIL.

    Ejemplo\(\PageIndex{8}\)

    Simplificar:

    1. \((3-2 \sqrt{7})(4-2 \sqrt{7})\)
    2. \((\sqrt[3]{x}-2)(\sqrt[3]{x}+4)\)

    Solución:

    a.

    \((3-2 \sqrt{7})(4-2 \sqrt{7})\)

    Multiplicar.

    \(12-6 \sqrt{7}-8 \sqrt{7}+4 \cdot 7\)

    Simplificar.

    \(12-6 \sqrt{7}-8 \sqrt{7}+28\)

    Combina términos similares.

    \(40-14 \sqrt{7}\)

    b.

    \((\sqrt[3]{x}-2)(\sqrt[3]{x}+4)\)

    Multiplicar.

    \(\sqrt[3]{x^{2}}+4 \sqrt[3]{x}-2 \sqrt[3]{x}-8\)

    Combina términos similares.

    \(\sqrt[3]{x^{2}}+2 \sqrt[3]{x}-8\)

    Ejercicio\(\PageIndex{15}\)

    Simplificar:

    1. \((6-3 \sqrt{7})(3+4 \sqrt{7})\)
    2. \((\sqrt[3]{x}-2)(\sqrt[3]{x}-3)\)
    Contestar
    1. \(-66+15 \sqrt{7}\)
    2. \(\sqrt[3]{x^{2}}-5 \sqrt[3]{x}+6\)
    Ejercicio\(\PageIndex{16}\)

    Simplificar:

    1. \((2-3 \sqrt{11})(4-\sqrt{11})\)
    2. \((\sqrt[3]{x}+1)(\sqrt[3]{x}+3)\)
    Contestar
    1. \(41-14 \sqrt{11}\)
    2. \(\sqrt[3]{x^{2}}+4 \sqrt[3]{x}+3\)
    Ejemplo\(\PageIndex{9}\)

    Simplificar:\((3 \sqrt{2}-\sqrt{5})(\sqrt{2}+4 \sqrt{5})\)

    Solución:

    \((3 \sqrt{2}-\sqrt{5})(\sqrt{2}+4 \sqrt{5})\)

    Multiplicar.

    \(3 \cdot 2+12 \sqrt{10}-\sqrt{10}-4 \cdot 5\)

    Simplificar.

    \(6+12 \sqrt{10}-\sqrt{10}-20\)

    Combina términos similares.

    \(-14+11 \sqrt{10}\)

    Ejercicio\(\PageIndex{17}\)

    Simplificar:\((5 \sqrt{3}-\sqrt{7})(\sqrt{3}+2 \sqrt{7})\)

    Contestar

    \(1+9 \sqrt{21}\)

    Ejercicio\(\PageIndex{18}\)

    Simplificar:\((\sqrt{6}-3 \sqrt{8})(2 \sqrt{6}+\sqrt{8})\)

    Contestar

    \(-12-20 \sqrt{3}\)

    Reconocer algunos productos especiales facilitó nuestro trabajo cuando multiplicamos binomios antes. Esto es cierto cuando multiplicamos los radicales, también. Aquí se muestran las fórmulas especiales de productos que utilizamos.

    Productos Especiales

    Cuadrados Binomiales

    \(\begin{array}{l}{(a+b)^{2}=a^{2}+2 a b+b^{2}} \\ {(a-b)^{2}=a^{2}-2 a b+b^{2}}\end{array}\)

    Producto de Conconjugados

    \((a+b)(a-b)=a^{2}-b^{2}\)

    Usaremos las fórmulas especiales de productos en los siguientes ejemplos. Comenzaremos con el Producto del Patrón de Cuadrados Binomiales.

    Ejemplo\(\PageIndex{10}\)

    Simplificar:

    1. \(2+\sqrt{3})^{2}\)
    2. \((4-2 \sqrt{5})^{2}\)

    Solución:

    a.

      .
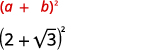    Multiplicar usando el Producto del Patrón de Cuadrados Binomiales. .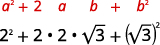
    Simplificar. .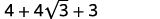
    Combina términos similares. .
    Cuadro 8.4.1

    b.

    Cuadro 8.4.2
     

    .
    Múltiple, utilizando el Producto de Patrón Cuadrados Binomiales.

    .
    Simplificar.

    .
     

    .
    Combina términos similares.

    .
    Ejercicio\(\PageIndex{19}\)

    Simplificar:

    1. \((10+\sqrt{2})^{2}\)
    2. \((1+3 \sqrt{6})^{2}\)
    Contestar
    1. \(102+20 \sqrt{2}\)
    2. \(55+6 \sqrt{6}\)
    Ejercicio\(\PageIndex{20}\)

    Simplificar:

    1. \((6-\sqrt{5})^{2}\)
    2. \((9-2 \sqrt{10})^{2}\)
    Contestar
    1. \(41-12 \sqrt{5}\)
    2. \(121-36 \sqrt{10}\)

    En el siguiente ejemplo, utilizaremos el Patrón Producto de Conconjugados. Observe que el producto final no tiene radical.

    Ejemplo\(\PageIndex{11}\)

    Simplificar:\((5-2 \sqrt{3})(5+2 \sqrt{3})\)

    Solución:

     

    .
    Multiplicar usando el Patrón de Producto de Conconjugados.

    .
    Simplificar.

    .
     

    .
    Cuadro 8.4.3
    Ejercicio\(\PageIndex{21}\)

    Simplificar:\((3-2 \sqrt{5})(3+2 \sqrt{5})\)

    Contestar

    \(-11\)

    Ejercicio\(\PageIndex{22}\)

    Simplificar:\((4+5 \sqrt{7})(4-5 \sqrt{7})\)

    Contestar

    \(-159\)

    Acceda a estos recursos en línea para obtener instrucción y práctica adicionales con sumar, restar y multiplicar expresiones radicales.

    • Multiplicar Sumando Restos Radicales
    • Multiplicando Productos Especiales: Binomios Cuadrados Que Contienen Raíces Cuadradas
    • Multiplicar conjugados

    Conceptos clave

    • Propiedad del producto de las raíces
      • Para cualquier número real,\(\sqrt[n]{a}\) y\(\sqrt[n]{b}\), y para cualquier entero\(n≥2\)\(\sqrt[n]{a b}=\sqrt[n]{a} \cdot \sqrt[n]{b}\) y\(\sqrt[n]{a} \cdot \sqrt[n]{b}=\sqrt[n]{a b}\)
    • Productos Especiales

    \(\begin{array}{c c}{\text { Binomial Squares }}& {\text{Product of Conjugates}} \\ {(a+b)^{2}=a^{2}+2 a b+b^{2}} & {(a+b)(a-b)=a^{2}-b^{2}} \\ {(a-b)^{2}=a^{2}-2 a b+b^{2}}\end{array}\)

    Glosario

    como radicales
    Como radicales son expresiones radicales con el mismo índice y el mismo radicando.

    This page titled 8.5: Sumar, restar y multiplicar expresiones radicales is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by OpenStax via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.