Saltar al contenido principal
LibreTexts Español

9.3E: Ejercicios

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    112685

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    La práctica hace la perfección

    EJERCICIOS 1 - 4: Completar el Cuadrado de una Expresión Binomial

    En los siguientes ejercicios, completa el cuadrado para hacer un trinomio cuadrado perfecto. Después escribe el resultado como un binomio al cuadrado.

      1. \(m^{2}-24 m\)
      2. \(x^{2}-11 x\)
      3. \(p^{2}-\frac{1}{3} p\)
      1. \(n^{2}-16 n\)
      2. \(y^{2}+15 y\)
      3. \(q^{2}+\frac{3}{4} q\)
      1. \(p^{2}-22 p\)
      2. \(y^{2}+5 y\)
      3. \(m^{2}+\frac{2}{5} m\)
      1. \(q^{2}-6 q\)
      2. \(x^{2}-7 x\)
      3. \(n^{2}-\frac{2}{3} n\)
    Contestar

    1. a.\((m-12)^{2}\) b.\(\left(x-\frac{11}{2}\right)^{2}\) c.\(\left(p-\frac{1}{6}\right)^{2}\)

    3. a.\((p-11)^{2}\) b.\(\left(y+\frac{5}{2}\right)^{2}\) c.\(\left(m+\frac{1}{5}\right)^{2}\)

    EJERCICIOS 5 - 28: Resolver ecuaciones cuadráticas de la forma\(x^{2}+b x+c=0\) by Completing the Square

    En los siguientes ejercicios, resuelva completando la plaza.

    5. \(u^{2}+2 u=3\)

    6. \(z^{2}+12 z=-11\)

    7. \(x^{2}-20 x=21\)

    8. \(y^{2}-2 y=8\)

    9. \(m^{2}+4 m=-44\)

    10. \(n^{2}-2 n=-3\)

    11. \(r^{2}+6 r=-11\)

    12. \(t^{2}-14 t=-50\)

    13. \(a^{2}-10 a=-5\)

    14. \(b^{2}+6 b=41\)

    15. \(x^{2}+5 x=2\)

    16. \(y^{2}-3 y=2\)

    17. \(u^{2}-14 u+12=-1\)

    18. \(z^{2}+2 z-5=2\)

    19. \(r^{2}-4 r-3=9\)

    20. \(t^{2}-10 t-6=5\)

    21. \(v^{2}=9 v+2\)

    22. \(w^{2}=5 w-1\)

    23. \(x^{2}-5=10 x\)

    24. \(y^{2}-14=6 y\)

    25. \((x+6)(x-2)=9\)

    26. \((y+9)(y+7)=80\)

    27. \((x+2)(x+4)=3\)

    28. \((x-2)(x-6)=5\)

    Contestar

    5. \(u=-3, u=1\)

    7. \(x=-1, x=21\)

    9. \(m=-2 \pm 2 \sqrt{10} i\)

    11. \(r=-3 \pm \sqrt{2} i\)

    13. \(a=5 \pm 2 \sqrt{5}\)

    15. \(x=-\frac{5}{2} \pm \frac{\sqrt{33}}{2}\)

    17. \(u=1, u=13\)

    19. \(r=-2, r=6\)

    21. \(v=\frac{9}{2} \pm \frac{\sqrt{89}}{2}\)

    23. \(x=5 \pm \sqrt{30}\)

    25. \(x=-7, x=3\)

    27. \(x=-5, x=-1\)

    EJERCICIOS 29 - 40: Resolver ecuaciones cuadráticas de la forma\(a x^{2}+b x+c=0\) by Completing the Square

    En los siguientes ejercicios, resuelva completando la plaza.

    29. \(3 m^{2}+30 m-27=6\)

    30. \(2 x^{2}-14 x+12=0\)

    31. \(2 n^{2}+4 n=26\)

    32. \(5 x^{2}+20 x=15\)

    33. \(2 c^{2}+c=6\)

    34. \(3 d^{2}-4 d=15\)

    35. \(2 x^{2}+7 x-15=0\)

    36. \(3 x^{2}-14 x+8=0\)

    37. \(2 p^{2}+7 p=14\)

    38. \(3 q^{2}-5 q=9\)

    39. \(5 x^{2}-3 x=-10\)

    40. \(7 x^{2}+4 x=-3\)

    Contestar

    29. \(m=-11, m=1\)

    31. \(n=1 \pm \sqrt{14}\)

    33. \(c=-2, c=\frac{3}{2}\)

    35. \(x=-5, x=\frac{3}{2}\)

    37. \(p=-\frac{7}{4} \pm \frac{\sqrt{161}}{4}\)

    39. \(x=\frac{3}{10} \pm \frac{\sqrt{191}}{10} i\)

    EJERCICIOS 41 - 42: ejercicios de escritura

    41. Resolver la ecuación\(x^{2}+10 x=-25\)

    1. mediante el uso de la propiedad Raíz Cuadrada
    2. al Completar la Plaza
    3. ¿Qué método prefieres? ¿Por qué?

    42. Resuelve la ecuación\(y^{2}+8y=48\) completando el cuadrado y explica todos tus pasos.

    Contestar

    41. Las respuestas variarán

    Autocomprobación

    a. después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.

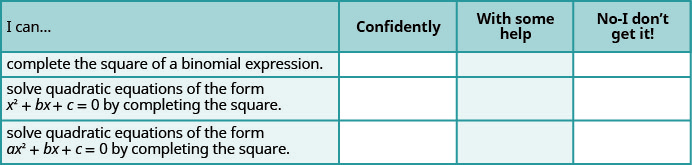
    Esta tabla proporciona una lista de verificación para evaluar el dominio de los objetivos de esta sección. Elige cómo responderías a la declaración “Puedo completar el cuadrado de una expresión binomial.††œconfiadamente, †“con alguna ayuda, †o †œno, donâ €™ t lo conseguirâ € Elige como responderías a la sentencia “Puedo resolver ecuaciones cuadráticas de la forma x cuadrado más b veces x más c es igual a 0 por completando el cuadrado.†œconfiadamente, †“with some help, †o “no, I donâ €™ t get it.†Elige como responderías a la sentencia “I puedo resolver ecuaciones cuadráticas de la forma a veces x al cuadrado más b por x más c es igual a 0 completando el cuadrado.†“confiadamente, †“with some help, †o â €œNo, no lo conseguido’ t lo consigue.â€
    Figura 9.2.103

    b. Después de revisar esta lista de verificación, ¿qué harás para tener confianza en todos los objetivos?

    This page titled 9.3E: Ejercicios is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by OpenStax via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.