Saltar al contenido principal
LibreTexts Español

9.4E: Ejercicios

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    112666

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    La práctica hace la perfección

    EJERCICIOS 1 - 32: Resolver ecuaciones cuadráticas usando la fórmula cuadrá

    En los siguientes ejercicios, resuelva usando la Fórmula Cuadrática.

    1. \(4 m^{2}+m-3=0\)

    2. \(4 n^{2}-9 n+5=0\)

    3. \(2 p^{2}-7 p+3=0\)

    4. \(3 q^{2}+8 q-3=0\)

    5. \(p^{2}+7 p+12=0\)

    6. \(q^{2}+3 q-18=0\)

    7. \(r^{2}-8 r=33\)

    8. \(t^{2}+13 t=-40\)

    9. \(3 u^{2}+7 u-2=0\)

    10. \(2 p^{2}+8 p+5=0\)

    11. \(2 a^{2}-6 a+3=0\)

    12. \(5 b^{2}+2 b-4=0\)

    13. \(x^{2}+8 x-4=0\)

    14. \(y^{2}+4 y-4=0\)

    15. \(3 y^{2}+5 y-2=0\)

    16. \(6 x^{2}+2 x-20=0\)

    17. \(2 x^{2}+3 x+3=0\)

    18. \(2 x^{2}-x+1=0\)

    19. \(8 x^{2}-6 x+2=0\)

    20. \(8 x^{2}-4 x+1=0\)

    21. \((v+1)(v-5)-4=0\)

    22. \((x+1)(x-3)=2\)

    23. \((y+4)(y-7)=18\)

    24. \((x+2)(x+6)=21\)

    25. \(\dfrac{1}{4} m^{2}+\dfrac{1}{12} m=\dfrac{1}{3}\)

    26. \(\dfrac{1}{3} n^{2}+n=-\dfrac{1}{2}\)

    27. \(\dfrac{3}{4} b^{2}+\dfrac{1}{2} b=\dfrac{3}{8}\)

    28. \(\dfrac{1}{9} c^{2}+\dfrac{2}{3} c=3\)

    29. \(16 c^{2}+24 c+9=0\)

    30. \(25 d^{2}-60 d+36=0\)

    31. \(25 q^{2}+30 q+9=0\)

    32. \(16 y^{2}+8 y+1=0\)

    Contestar

    1. \(m=-1, m=\dfrac{3}{4}\)

    3. \(p=\dfrac{1}{3}, p=2\)

    5. \(p=-4, p=-3\)

    7. \(r=-3, r=11\)

    9. \(u=\dfrac{-7 \pm \sqrt{73}}{6}\)

    11. \(a=\dfrac{3 \pm \sqrt{3}}{2}\)

    13. \(x=-4 \pm 2 \sqrt{5}\)

    15. \(y=-\dfrac{2}{3}, y=-1\)

    17. \(x=-\dfrac{3}{4} \pm \dfrac{\sqrt{15}}{4} i\)

    19. \(x=\dfrac{3}{8} \pm \dfrac{\sqrt{7}}{8} i\)

    21. \(v=2 \pm 2 \sqrt{2}\)

    23. \(y=-4, y=7\)

    25. \(m=1, m=\dfrac{-4}{3}\)

    27. \(b=\dfrac{-2 \pm \sqrt{22}}{6}\)

    29. \(c=-\dfrac{3}{4}\)

    31. \(q=-\dfrac{3}{5}\)

    EJERCICIOS 33 - 36 Utilizar el discriminante para predecir el número de soluciones reales de una ecuación cuadrática

    En los siguientes ejercicios, determinar el número de soluciones reales para cada ecuación cuadrática.

      1. \(4 x^{2}-5 x+16=0\)
      2. \(36 y^{2}+36 y+9=0\)
      3. \(6 m^{2}+3 m-5=0\)
      1. \(9 v^{2}-15 v+25=0\)
      2. \(100 w^{2}+60 w+9=0\)
      3. \(5 c^{2}+7 c-10=0\)
      1. \(r^{2}+12 r+36=0\)
      2. \(8 t^{2}-11 t+5=0\)
      3. \(3 v^{2}-5 v-1=0\)
      1. \(25 p^{2}+10 p+1=0\)
      2. \(7 q^{2}-3 q-6=0\)
      3. \(7 y^{2}+2 y+8=0\)
    Contestar

    33. a. no hay soluciones reales b.\(1\) c.\(2\)

    35. a.\(1\) b. no hay soluciones reales c.\(2\)

    EJERCICIOS 37 - 40: Identificar el método más apropiado para resolver una ecuación cuadrática

    En los siguientes ejercicios, identifique el método más apropiado (Factoring, Raíz Cuadrada o Fórmula Cuadrática) a utilizar para resolver cada ecuación cuadrática. No resuelva.

      1. \(x^{2}-5 x-24=0\)
      2. \((y+5)^{2}=12\)
      3. \(14 m^{2}+3 m=11\)
      1. \((8 v+3)^{2}=81\)
      2. \(w^{2}-9 w-22=0\)
      3. \(4 n^{2}-10=6\)
      1. \(6 a^{2}+14=20\)
      2. \(\left(x-\dfrac{1}{4}\right)^{2}=\dfrac{5}{16}\)
      3. \(y^{2}-2 y=8\)
      1. \(8 b^{2}+15 b=4\)
      2. \(\dfrac{5}{9} v^{2}-\dfrac{2}{3} v=1\)
      3. \(\left(w+\dfrac{4}{3}\right)^{2}=\dfrac{2}{9}\)
    Contestar

    37. a. Factor b. Raíz cuadrada c. Fórmula cuadrática

    39. a. Fórmula cuadrática b. Raíz cuadrada c. Factor

    EJERCICIOS 41 - 42: Ejercicios de escritura
    1. Resolver la ecuación\(x^{2}+10 x=120\)
      1. completando la plaza
      2. usando la Fórmula Cuadrática
      3. ¿Qué método prefieres? ¿Por qué?
    2. Resolver la ecuación\(12 y^{2}+23 y=24\)
      1. completando la plaza
      2. usando la Fórmula Cuadrática
      3. ¿Qué método prefieres? ¿Por qué?
    Contestar

    41. Las respuestas variarán

    Autocomprobación

    a. después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.

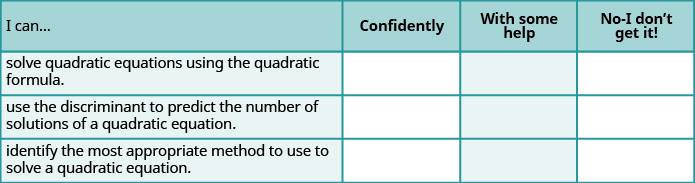
    Esta tabla proporciona una lista de verificación para evaluar el dominio de los objetivos de esta sección. Elige cómo responderías a la declaración “Puedo resolver ecuaciones cuadráticas usando la fórmula cuadrática.†“confiadamente, †“with alguna ayuda, †o †œno, I donâ €™ t get it.†Elige como responderías a la declaración“Puedo usar el discriminante para predecir el nÃomero de soluciones de un cuadrático ecuación.†“confiadamente, †“con alguna ayuda, †o †œno, no lo conseguido’ t loâ € Elige como responderías al enunciado “Puedo identificar el método más apropiado para usar para resolver una ecuacióncuadrática.â € â € œconfiadamente, †“con alguna ayuda, †o “no, donâ € t lo consigue.’
    Figura 9.3.87

    b. ¿Qué te dice esta lista de verificación sobre tu dominio de esta sección? ¿Qué pasos tomarás para mejorar?

    This page titled 9.4E: Ejercicios is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by OpenStax via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.