Saltar al contenido principal
LibreTexts Español

9.6E: Ejercicios

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    112665

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    La práctica hace la perfección

    Ejercicio\(\PageIndex{15}\) Solve Applications Modeled by Quadratic Equations

    En los siguientes ejercicios, resuelve usando cualquier método.

    1. El producto de dos números impares consecutivos es\(255\). Encuentra los números.
    2. El producto de dos números pares consecutivos es\(360\). Encuentra los números.
    3. El producto de dos números pares consecutivos es\(624\). Encuentra los números.
    4. El producto de dos números impares consecutivos es\(1,023\). Encuentra los números.
    5. El producto de dos números impares consecutivos es\(483\). Encuentra los números.
    6. El producto de dos números pares consecutivos es\(528\). Encuentra los números.
    Contestar

    1. Dos números impares consecutivos cuyo producto es\(255\)\(15\) y\(17\), y\(−15\) y\(−17\).

    3. El primer y segundo números impares consecutivos son\(24\) y\(26\), y\(−26\) y\(−24\).

    5. Dos números impares consecutivos cuyo producto es\(483\)\(21\) y\(23\), y\(−21\) y\(−23\).

    Ejercicio\(\PageIndex{16}\) Solve Applications Modeled by Quadratic Equations

    En los siguientes ejercicios, resuelve usando cualquier método. Redondea tus respuestas a la décima más cercana, si es necesario.

    1. Un triángulo con área de pulgadas\(45\) cuadradas tiene una altura que es dos menos de cuatro veces la base Encuentra la base y la altura del triángulo.
    2. La base de un triángulo es seis más del doble de la altura. El área del triángulo es de yardas\(88\) cuadradas. Encuentra la base y la altura del triángulo.
    3. El área de un lecho de flores triangular en el parque tiene una superficie de pies\(120\) cuadrados. La base es\(4\) pies más larga que el doble de la altura. ¿Cuáles son la base y la altura del triángulo?
    4. En el gimnasio cuelga una pancarta triangular para el campeonato de basquetbol. Tiene una superficie de pies\(75\) cuadrados. ¿Cuál es la longitud de la base y la altura, si la base es dos tercios de la altura?
    5. La longitud de una entrada rectangular es de cinco pies más de tres veces el ancho. El área es de pies\(50\) cuadrados. Encuentra el largo y ancho del camino de entrada.
    6. Un césped rectangular tiene área de yardas\(140\) cuadradas. Su longitud es de seis yardas menos del doble de su ancho. ¿Cuál es el largo y ancho del césped?
    7. Una mesa rectangular para el comedor tiene una superficie de pies\(24\) cuadrados. El largo es de dos pies más que el doble del ancho de la mesa. Encuentra el largo y ancho de la mesa.
    8. La nueva computadora tiene una superficie de pulgadas\(168\) cuadradas. Si el ancho es\(5.5\) pulgadas menos que el largo, ¿cuáles son las dimensiones de la computadora?
    9. La hipotenusa de un triángulo rectángulo es el doble de la longitud de una de sus patas. La longitud de la otra pierna es de tres pies. Encuentra las longitudes de los tres lados del triángulo.
    10. La hipotenusa de un triángulo rectángulo mide\(10\) cm de largo. Una de las patas del triángulo es tres veces mayor que la longitud de la otra pierna. Redondear a la décima más cercana. Encuentra las longitudes de los tres lados del triángulo.
    11. Un jardín rectangular se dividirá en dos parcelas cercándolo en diagonal. La distancia diagonal de una esquina del jardín a la esquina opuesta es cinco yardas más larga que el ancho del jardín. La longitud del jardín es tres veces la anchura. Encuentra la longitud de la diagonal del jardín.
    La imagen muestra un segmento rectangular de pasto con barda alrededor de 4 lados y a través de la diagonal. El lado vertical del rectángulo está etiquetado con w y el lado horizontal con la etiqueta 3 w. La cerca diagonal está etiquetada con w más 5.
    Figura 9.5.44

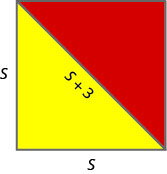
    12. Las banderas náuticas se utilizan para representar letras del alfabeto. La bandera para la letra, O consiste en un triángulo rectángulo amarillo y un triángulo rectángulo rojo que se cosen juntos a lo largo de su hipotenusa para formar un cuadrado. La hipotenusa de los dos triángulos es tres pulgadas más larga que un lado de la bandera. Encuentra la longitud del costado de la bandera.

    En la imagen se muestra un cuadrado con longitudes laterales s. El cuadrado se divide en dos triángulos con una diagonal. El triángulo superior es rojo y el triángulo inferior es amarillo. La diagonal está etiquetada como s más 3.
    Figura 9.5.45

    13. Gerry planea colocar una escalera\(25\) de pie contra el costado de su casa para limpiar sus canalones. El fondo de la escalera estará a\(5\) pies de la casa. ¿Cómo para arriba el costado de la casa alcanzará la escalera?

    14. John tiene un trozo de cuerda\(10\) -pie que quiere usar para sostener su árbol\(8\) -foot. ¿A qué distancia de la base del árbol debe asegurar la cuerda?

    15. Una flecha se dispara verticalmente hacia arriba a una velocidad de\(v_{0} = 220\) pies por segundo. Usa la fórmula del proyectil\(h=-16 t^{2}+v_{0} t\), para determinar cuándo la altura de la flecha será\(400\) pies.

    16. Un cohete de fuegos artificiales es disparado hacia arriba a una velocidad de\(640\) pies/seg. Usa la fórmula del proyectil\(h=-16 t^{2}+v_{0} t\) para determinar cuándo la altura del cohete de fuegos artificiales será de\(1200\) pies.

    17. Se dispara una bala hacia arriba desde una pistola BB con velocidad inicial\(1120\) pies por segundo a una altura inicial de\(8\) pies. Usa la fórmula\(h=-16 t^{2}+v_{0} t+8\) para determinar cuántos segundos tardará en que la bala llegue al suelo. (Es decir, ¿cuándo lo hará\(h=0\)?)

    18. Se deja caer una piedra desde una plataforma de\(196\) -pie. Usa la fórmula\(h=-16 t^{2}+v_{0} t+196\) para determinar cuántos segundos tardará en que la piedra golpee el suelo. (Ya que la piedra se deja caer,\(v_{0}=0\).)

    19. El empresario tomó un pequeño avión para un rápido vuelo por la costa para una reunión de almuerzo y luego regresó a su casa. El avión voló un total de\(4\) horas y en cada sentido el viaje era de\(200\) millas. ¿Cuál fue la velocidad del viento que afectó al avión que volaba a una velocidad de\(120\) mph?

    20. La pareja tomó un pequeño avión para un rápido vuelo hasta la región vinícola para una cena romántica y luego regresó a casa. El avión voló un total de\(5\) horas y en cada sentido el viaje era de\(300\) millas. Si el avión volaba a\(125\) mph, ¿cuál fue la velocidad del viento que afectó al avión?

    21. Roy subió en kayak por el río y luego regresó en un tiempo total de\(6\) horas. El viaje era de\(4\) millas en cada sentido y la corriente era difícil. Si Roy navegaba en kayak a una velocidad de\(5\) mph, ¿cuál era la velocidad de la corriente?

    22. Rick remando río arriba, pasó la noche acampando, y luego remando de regreso. Pasaba\(10\) horas remando y el campamento estaba a\(24\) kilómetros de distancia. Si Rick navegaba en kayak a una velocidad de\(5\) mph, ¿cuál era la velocidad de la corriente?

    23. Dos pintores pueden pintar una habitación en\(2\) horas si trabajan juntos. El pintor menos experimentado tarda\(3\) horas más que el pintor más experimentado en terminar el trabajo. ¿Cuánto tiempo tarda cada pintor en pintar la habitación individualmente?

    24. Dos jardineros pueden hacer el mantenimiento semanal del patio en\(8\) minutos si trabajan juntos. El jardinero mayor tarda\(12\) minutos más que el jardinero más joven en terminar el trabajo solo. ¿Cuánto tiempo tarda cada jardinero en realizar el mantenimiento semanal del patio individualmente?

    25. Dos máquinas tardan dos horas en fabricar\(10,000\) piezas. Si la Máquina #1 puede hacer el trabajo sola en una hora menos de lo que la Máquina #2 puede hacer el trabajo, ¿cuánto tiempo tarda cada máquina en fabricar\(10,000\) piezas sola?

    26. Sully está teniendo una fiesta y quiere llenar su piscina. Si solo usa su manguera tarda\(2\) horas más que si solo usa la manguera de su vecino. Si usa ambas mangueras juntas, la alberca se llena en\(4\) horas. ¿Cuánto tiempo tarda cada manguera en llenar la piscina?

    Contestar

    1. El ancho del triángulo es\(5\) pulgadas y la altura es\(18\) pulgadas.

    3. La base es\(24\) pies y la altura del triángulo es\(10\) pies.

    5. La longitud del camino de entrada es\(15.0\) pies y el ancho es\(3.3\) pies.

    7. El largo de la mesa es\(8\) pies y el ancho es\(3\) pies.

    9. La longitud de las patas del triángulo rectángulo son\(3.2\) y\(9.6\) cm.

    11. La longitud de la esgrima diagonal es de\(7.3\) yardas.

    13. La escalera alcanzará\(24.5\) los pies en el costado de la casa.

    15. La flecha alcanzará\(400\) pies en su camino hacia arriba en\(2.2\) segundos y en el camino hacia abajo en\(11.6\) segundos.

    17. El balazo tardará\(70\) segundos en llegar al suelo.

    19. La velocidad del viento era\(49\) mph.

    21. La velocidad de la corriente era\(4.3\) mph.

    23. El pintor menos experimentado tarda\(6\) horas y el pintor experimentado tarda\(3\) horas en hacer el trabajo solo.

    25. La máquina #1 toma\(3.6\) horas y la máquina #2 tarda\(4.6\) horas en hacer el trabajo sola.

    Ejercicio\(\PageIndex{17}\) writing exercises
    1. Informar un problema que involucre el producto de dos enteros impares consecutivos.
      1. Comience eligiendo dos enteros impares consecutivos. ¿Cuáles son tus enteros?
      2. ¿Cuál es el producto de tus enteros?
      3. Resuelve la ecuación\(n(n+2)=p\), donde\(p\) está el producto que encontraste en la parte (b).
      4. ¿Obtuviste los números con los que empezaste?
    2. Informar un problema que involucre el producto de dos enteros pares consecutivos.
      1. Comience eligiendo dos enteros pares consecutivos. ¿Cuáles son tus enteros?
      2. ¿Cuál es el producto de tus enteros?
      3. Resuelve la ecuación\(n(n+2)=p\), donde\(p\) está el producto que encontraste en la parte (b).
      4. ¿Obtuviste los números con los que empezaste?
    Contestar

    1. Las respuestas variarán.

    Autocomprobación

    a. después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.

    Esta tabla proporciona una lista de verificación para evaluar el dominio de los objetivos de esta sección. Elige cómo responderías a la declaración “Puedo resolver aplicaciones de la fórmula cuadrática.†“confiadamente, †“con alguna ayuda, †o †œno, no lo conseguidoâ €™ t lo conseguirâ €
    Figura 9.5.46

    b. después de mirar la lista de verificación, ¿cree que está bien preparado para la siguiente sección? ¿Por qué o por qué no?

    This page titled 9.6E: Ejercicios is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by OpenStax via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.