Saltar al contenido principal
LibreTexts Español

9.7E: Funciones Cuadráticas Gráficas Usando Propiedades (Ejercicios)

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    112696

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    La práctica hace la perfección

    Ejercicios 1 - 4: Reconocer la Gráfica de una Función Cuadrática

    En los siguientes ejercicios, grafica las funciones trazando puntos.

    1. \(f(x)=x^{2}+3\)

    2. \(f(x)=x^{2}-3\)

    3. \(y=-x^{2}+1\)

    4. \(f(x)=-x^{2}-1\)

    Contestar

    1.

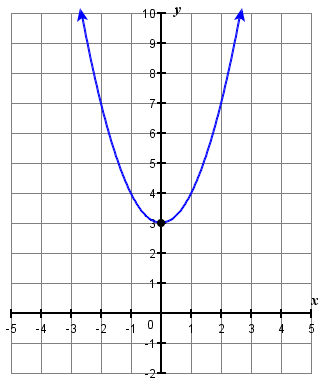
    clipboard_eb78a0f78325e7c8a9cceea709788ca1d.png

    3.

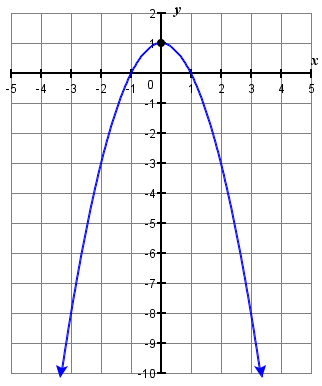
    clipboard_ef318ed788d73edacb2b69f9a778e9ce9.png

    Ejercicios 5 - 8: Reconocer la Gráfica de una Función Cuadrática

    Para cada uno de los siguientes ejercicios, determine si la parábola se abre hacia arriba o hacia abajo.

    5. a.\(f(x)=-2 x^{2}-6 x-7\) b.\(f(x)=6 x^{2}+2 x+3\)

    6. a.\(f(x)=4 x^{2}+x-4\) b.\(f(x)=-9 x^{2}-24 x-16\)

    7. a.\(f(x)=-3 x^{2}+5 x-1\) b.\(f(x)=2 x^{2}-4 x+5\)

    8. a.\(f(x)=x^{2}+3 x-4\) b.\(f(x)=-4 x^{2}-12 x-9\)

    Contestar

    5. a. abajo b. arriba

    7. a. abajo b. arriba

    Ejercicios 9 - 12: Encontrar el eje de simetría y vértice de una parábola

    En las siguientes funciones, encuentra

    1. La ecuación del eje de simetría
    2. El vértice de su gráfica

    9. \(f(x)=x^{2}+8 x-1\)

    10. \(f(x)=x^{2}+10 x+25\)

    11. \(f(x)=-x^{2}+2 x+5\)

    12. \(f(x)=-2 x^{2}-8 x-3\)

    Contestar

    9. a. Eje de simetría:\(x=-4\) b. Vértice:\((-4,-17)\)

    11. a. Eje de simetría:\(x=1\) b. Vértice:\((1,2)\)

    Ejercicios 13 - 24: Encontrar las intercepciones de una parábola

    En los siguientes ejercicios, encuentra las intercepciones de la parábola cuya función se le da.

    13. \(f(x)=x^{2}+7 x+6\)

    14. \(f(x)=x^{2}+10 x-11\)

    15. \(f(x)=x^{2}+8 x+12\)

    16. \(f(x)=x^{2}+5 x+6\)

    17. \(f(x)=-x^{2}+8 x-19\)

    18. \(f(x)=-3 x^{2}+x-1\)

    19. \(f(x)=x^{2}+6 x+13\)

    20. \(f(x)=x^{2}+8 x+12\)

    21. \(f(x)=4 x^{2}-20 x+25\)

    22. \(f(x)=-x^{2}-14 x-49\)

    23. \(f(x)=-x^{2}-6 x-9\)

    24. \(f(x)=4 x^{2}+4 x+1\)

    Contestar

    13. \(y\)-interceptar:\((0,6)\);\(x\) -intercepción (s):\((-1,0), (-6,0)\)

    15. \(y\)-interceptar:\((0,12)\);\(x\) -intercepción (s):\((-2,0), (-6,0)\)

    17. \(y\)-intercepción:\((0,-19)\);\(x\) -intercepción (s): ninguna

    19. \(y\)-intercepción:\((0,13)\);\(x\) -intercepción (s): ninguna

    21. \(y\)-interceptar:\((0,-16)\);\(x\) -intercepción (s):\((\frac{5}{2},0)\)

    23. \(y\)-interceptar:\((0,9)\);\(x\) -intercepción (s):\((-3,0)\)

    Ejercicios 25 - 42: Funciones Cuadráticas Gráficas Usando Propiedades

    En los siguientes ejercicios, grafica la función usando sus propiedades.

    25. \(f(x)=x^{2}+6 x+5\)

    26. \(f(x)=x^{2}+4 x-12\)

    27. \(f(x)=x^{2}+4 x+3\)

    28. \(f(x)=x^{2}-6 x+8\)

    29. \(f(x)=9 x^{2}+12 x+4\)

    30. \(f(x)=-x^{2}+8 x-16\)

    31. \(f(x)=-x^{2}+2 x-7\)

    32. \(f(x)=5 x^{2}+2\)

    33. \(f(x)=2 x^{2}-4 x+1\)

    34. \(f(x)=3 x^{2}-6 x-1\)

    35. \(f(x)=2 x^{2}-4 x+2\)

    36. \(f(x)=-4 x^{2}-6 x-2\)

    37. \(f(x)=-x^{2}-4 x+2\)

    38. \(f(x)=x^{2}+6 x+8\)

    39. \(f(x)=5 x^{2}-10 x+8\)

    40. \(f(x)=-16 x^{2}+24 x-9\)

    41. \(f(x)=3 x^{2}+18 x+20\)

    42. \(f(x)=-2 x^{2}+8 x-10\)

    Contestar

    25.

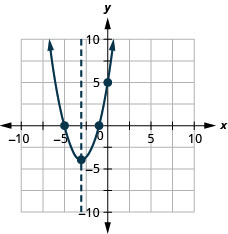
    Esta figura muestra una parábola de apertura hacia arriba graficada en el plano de la coordenada x y. El eje x del plano va de negativo 10 a 10. El eje y del plano va de negativo 10 a 10. La parábola tiene un vértice en (negativo 3, negativo 4). La intercepción y, punto (0, 5), se traza al igual que las intercepciones x, (negativo 5, 0) y (negativo 1, 0).
    Figura 9.6.136

    27.

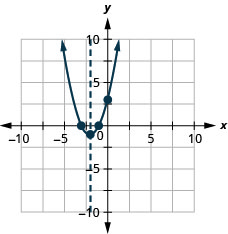
    Esta figura muestra una parábola de apertura hacia arriba graficada en el plano de la coordenada x y. El eje x del plano va de negativo 10 a 10. El eje y del plano va de negativo 10 a 10. La parábola tiene un vértice en (negativo 2, negativo 1). La intercepción y, punto (0, 3), se traza al igual que las intercepciones x, (negativo 3, 0) y (negativo 1, 0).
    Figura 9.6.137

    29.

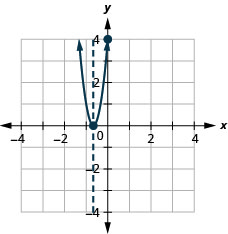
    Esta figura muestra una parábola de apertura hacia arriba graficada en el plano de la coordenada x y. El eje x del plano va de negativo 4 a 4. El eje y del plano va de negativo 4 a 4. La parábola tiene un vértice en (2 tercios negativos, 0). Se traza la intercepción y, punto (0, 4). El eje de simetría, x es igual a 2 tercios negativos, se traza como una línea vertical discontinua.
    Figura 9.6.138

    31.

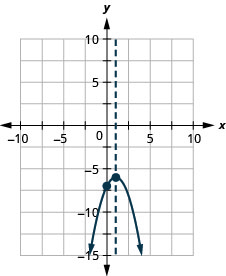
    Esta figura muestra una parábola de apertura hacia abajo graficada en el plano de la coordenada x y. El eje x del plano va de negativo 10 a 10. El eje y del plano va de negativo 15 a 10. La parábola tiene un vértice en (1, negativo 6). Se traza la intercepción y, punto (0, 7 negativo). El eje de simetría, x es igual a 1, se traza como una línea vertical discontinua.
    Figura 9.6.139

    33.

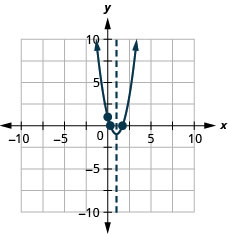
    Esta figura muestra una parábola de apertura hacia arriba graficada en el plano de la coordenada x y. El eje x del plano va de negativo 10 a 10. El eje y del plano va de negativo 10 a 10. La parábola tiene un vértice en (1, negativo 1). La intercepción y, punto (0, 1), se traza al igual que las intercepciones x, aproximadamente (0.3, 0) y (1.7, 0). El eje de simetría es la línea vertical x es igual a 1, trazada como una línea discontinua.
    Figura 9.6.140

    35.

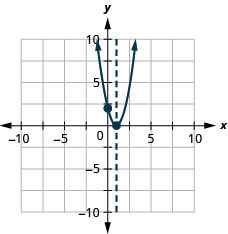
    Esta figura muestra una parábola de apertura hacia arriba graficada en el plano de la coordenada x y. El eje x del plano va de negativo 10 a 10. El eje y del plano va de negativo 10 a 10. La parábola tiene un vértice en (1, 0). Este punto es la única intercepción x. Se traza la intercepción y, punto (0, 2). El eje de simetría es la línea vertical x es igual a 1, trazada como una línea discontinua.
    Figura 9.6.141

    37.

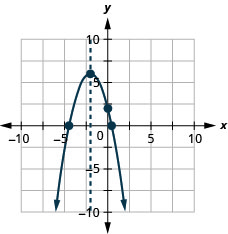
    Esta figura muestra una parábola de apertura hacia abajo graficada en el plano de la coordenada x y. El eje x del plano va de negativo 10 a 10. El eje y del plano va de negativo 10 a 10. La parábola tiene un vértice en (negativo 2, 6). La intercepción y, punto (0, 2), se traza al igual que las intercepciones x, aproximadamente (negativo 4.4, 0) y (0.4, 0). El eje de simetría es la línea vertical x es igual a 2, trazada como una línea discontinua.
    Figura 9.6.142

    39.

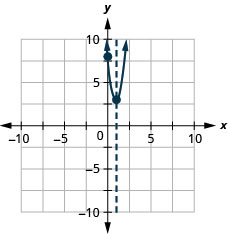
    Esta figura muestra una parábola de apertura hacia arriba graficada en el plano de la coordenada x y. El eje x del plano va de negativo 10 a 10. El eje y del plano va de negativo 10 a 10. La parábola tiene un vértice en (1, 3). Se traza la intercepción y, punto (0, 8); no hay intercepciones x. El eje de simetría es la línea vertical x es igual a 1, trazada como una línea discontinua.
    Figura 9.6.143

    41.

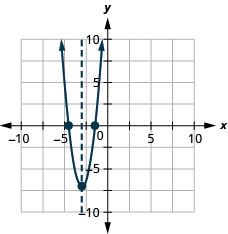
    Esta figura muestra una parábola de apertura hacia arriba graficada en el plano de la coordenada x y. El eje x del plano va de negativo 10 a 10. El eje y del plano va de negativo 10 a 10. La parábola tiene un vértice en (negativo 3, negativo 7). Las intercepciones x se trazan en los puntos aproximados (negativo 4.5, 0) y (negativo 1.5, 0). El eje de simetría es la línea vertical x igual a negativo 3, trazada como una línea discontinua.
    Figura 9.6.144
    Ejercicios 43 - 48: Resolver aplicaciones máximas y mínimas

    En los siguientes ejercicios, encuentra el valor máximo o mínimo de cada función.

    43. \(f(x)=2 x^{2}+x-1\)

    44. \(y=-4 x^{2}+12 x-5\)

    45. \(y=x^{2}-6 x+15\)

    46. \(y=-x^{2}+4 x-5\)

    47. \(y=-9 x^{2}+16\)

    48. \(y=4 x^{2}-49\)

    Contestar

    43. El valor mínimo es\(−\frac{9}{8}\) cuándo\(x=−\frac{1}{4}\).

    45. El valor máximo es\(6\) cuándo\(x=3\).

    47. El valor máximo es\(16\) cuándo\(x=0\).

    Ejercicios 49 - 60: Resolver aplicaciones máximas y mínimas

    En los siguientes ejercicios, resuelve. Respuestas redondas a la décima más cercana.

    49. Una flecha se dispara verticalmente hacia arriba desde una plataforma de\(45\) pies de altura a una velocidad de\(168\) pies/seg. Usa la función cuadrática\(h(t)=-16 t^{2}+168 t+45\) encuentra cuánto tiempo tardará la flecha en alcanzar su altura máxima, y luego encuentra la altura máxima.

    50. Una piedra se lanza verticalmente hacia arriba desde una plataforma que tiene\(20\) pies de altura a una velocidad de\(160\) pies/seg. Usa la función cuadrática\(h(t)=-16 t^{2}+160 t+20\) para encontrar cuánto tiempo tardará la piedra en alcanzar su altura máxima, y luego encontrar la altura máxima.

    51. Se lanza una pelota verticalmente hacia arriba desde el suelo con una velocidad inicial de\(109\) pies/seg. Usa la función cuadrática\(h(t)=-16 t^{2}+109 t+0\) para encontrar cuánto tiempo tardará la pelota en alcanzar su altura máxima, y luego encontrar la altura máxima.

    52. Se lanza una pelota verticalmente hacia arriba desde el suelo con una velocidad inicial de\(122\) pies/seg. Usa la función cuadrática\(h(t)=-16 t^{2}+122 t+0\) para encontrar cuánto tiempo tardará la pelota en alcanzar su altura máxima, y luego encontrar la altura máxima.

    53. El dueño de una tienda de informática estima que al cobrar\(x\) dólares cada uno por una determinada computadora, puede vender\(40 − x\) computadoras cada semana. La función cuadrática\(R(x)=-x^{2}+40 x\) se utiliza para encontrar los ingresos,\(R\), recibidos cuando el precio de venta de una computadora es\(x\), Encontrar el precio de venta que le dará los ingresos máximos, y luego encontrar el monto de los ingresos máximos.

    54. Un minorista que vende mochilas estima que al venderlas por\(x\) dólares cada una, podrá vender\(100 − x\) mochilas al mes. La función cuadrática\(R(x)=-x^{2}+100 x\) se utiliza para encontrar el\(R\), recibido cuando es el precio de venta de una mochila\(x\). Encuentra el precio de venta que le dará los ingresos máximos, y luego encuentra el monto de los ingresos máximos.

    55. Un minorista que vende botas de moda estima que al venderlas por\(x\) dólares cada una, podrá vender\(70 − x\) botas a la semana. Utilice la función cuadrática\(R(x)=-x^{2}+70 x\) para encontrar los ingresos recibidos cuando el precio promedio de venta de un par de botas de moda es\(x\). Encuentra el precio de venta que le dará los ingresos máximos, y luego encuentra el monto de los ingresos máximos por día.

    56. Una compañía de telefonía celular estima que al cobrar\(x\) dólares cada uno por un determinado celular, pueden vender\(8 − x\) celulares por día. Utilice la función cuadrática\(R(x)=-x^{2}+8 x\) para encontrar los ingresos recibidos por día cuando el precio de venta de un celular es\(x\). Encuentra el precio de venta que les dará los ingresos máximos por día, y luego encuentra el monto de los ingresos máximos.

    57. Un ranchero va a cercar tres lados de un corral junto a un río. Necesita maximizar el área del corral usando\(240\) pies de esgrima. La ecuación cuadrática\(A(x)=x(240-2 x)\) da el área del corral,\(A\), para la longitud,\(x\), del corral a lo largo del río. Encuentra la longitud del corral a lo largo del río que dará el área máxima, y luego encuentra el área máxima del corral.

    58. Un veterinario encierra un área rectangular para correr al aire libre contra su edificio para los perros que cuida. Necesita maximizar el área usando\(100\) pies de esgrima. La función cuadrática\(A(x)=x(100-2 x)\) da el área,\(A\), de la carrera canina por la longitud\(x\),, del edificio que bordeará la carrera canina. Encuentra la longitud del edificio que debe bordear la carrera canina para dar el área máxima, y luego encontrar el área máxima de la carrera canina.

    59. Un dueño de tierra planea construir un patio cercado en rectangular detrás de su cochera, usando su cochera como una de las “paredes”. Quiere maximizar el área usando\(80\) pies de esgrima. La función cuadrática\(A(x)=x(80-2 x)\) da el área del patio, donde\(x\) está el ancho de un lado. Encuentra el área máxima del patio.

    60. Una familia de tres niños pequeños acaba de mudarse a una casa con un patio que no está cercado. El dueño anterior les dio\(300\) pies de esgrima para que los usaran para encerrar parte de su patio trasero. Utilice la función cuadrática\(A(x)=x(300-2 x)\) para determinar el área máxima del patio cercado.

    Contestar

    49. En\(5.3\) segundos la flecha alcanzará la altura máxima de\(486\) ft.

    51. En\(3.4\) segundos la pelota alcanzará su máxima altura de\(185.6\) pies.

    53. \(20\)computadoras darán el máximo de $\(400\) en recibos.

    55. Podrá vender\(35\) pares de botas al ingreso máximo de $\(1,225\).

    57. La longitud del costado a lo largo del río del corral es de\(120\) pies y el área máxima es de pies\(7,200\) cuadrados.

    59. El área máxima del patio es\(800\) pies.

    Ejercicios 61 - 64: Ejercicios de escritura

    61. ¿En qué se\(f(x)=x^{2}−1\) diferencian las gráficas de las funciones\(f(x)=x^{2}\) y? Los graficamos al inicio de esta sección. ¿Cuál es la diferencia entre sus gráficas? ¿Cómo son iguales sus gráficas?

    62. Explicar el proceso de encontrar el vértice de una parábola.

    63. Explicar cómo encontrar las intercepciones de una parábola.

    64. ¿Cómo puedes usar el discriminante cuando estás graficando una función cuadrática?

    Contestar

    1. Las respuestas variarán.

    3. Las respuestas variarán.

    Autocomprobación

    a. después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.

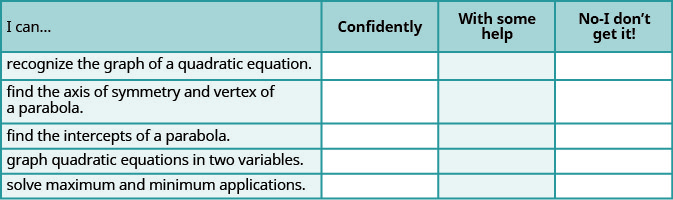
    Esta tabla proporciona una lista de verificación para evaluar el dominio de los objetivos de esta sección. Elige cómo responderías a la declaración “Puedo reconocer la gráfica de una ecuación cuadrática.â € â € œconfiadamente, †“con alguna ayuda, †o †œno, no, no lo consiga.â € Elige como responderías a la declaraciónâ € Puedo encontrar el eje de simetría y vértice de una parabola.â € â € â € â € â € œConfiadamente, †€œcon™ alguna ayuda, †o “no, yo donâ €™ t lo consigoâ € Elige como responderías a la declaración “Puedo encontrar las intercepciones de una parabola.††“confiadamente, ††“con alguna ayuda, †o “no, yo donâ €™ t lo conseguiríaâ € Elige como responderías a la declaraciónâ € Puedo graficar cuadrático ecuaciones en dos variables.††œConfiadamente, †“con alguna ayuda, †o †œno, yo donâ €™ t lo consigoâ € Elige como responderías al enunciado “Puedo resolver las solicitudes máximas y mínimas. â € â € œconfiadamente, †“con alguna ayuda, †o †œno, no lo consigo.’
    Figura 9.6.145

    b. después de mirar la lista de verificación, ¿cree que está bien preparado para la siguiente sección? ¿Por qué o por qué no?

    This page titled 9.7E: Funciones Cuadráticas Gráficas Usando Propiedades (Ejercicios) is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by OpenStax via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.