10.2: Búsqueda de funciones compuestas e inversas
- Page ID
- 112513
Al final de esta sección, podrás:
- Buscar y evaluar funciones compuestas
- Determinar si una función es uno a uno
- Encontrar la inversa de una función
Antes de comenzar, toma este cuestionario de preparación.
- Si\(f(x)=2 x-3\) y\(g(x)=x^{2}+2 x-3\), encuentra\(f(4)\).
Si te perdiste este problema, revisa el Ejemplo 3.48. - Resolver para\(x\),\(3x+2y=12\).
Si te perdiste este problema, revisa el Ejemplo 2.31. - Simplificar:\(5 \frac{(x+4)}{5}-4\).
Si te perdiste este problema, revisa el Ejemplo 1.25.
En este capítulo, presentaremos dos nuevos tipos de funciones, funciones exponenciales y funciones logarítmicas. Estas funciones se utilizan ampliamente en los negocios y las ciencias como veremos.
Buscar y evaluar funciones compuestas
Antes de introducir las funciones, necesitamos mirar otra operación sobre funciones llamada composición. En composición, la salida de una función es la entrada de una segunda función. Para funciones\(f\) y\(g\), la composición está escrita\(f∘g\) y está definida por\((f∘g)(x)=f(g(x))\).
Leemos\(f(g(x))\) como “\(f\)\(g\)de”\(x\).
Para hacer una composición, la salida de la primera función,\(g(x)\), se convierte en la entrada de la segunda función\(f\),, y así debemos estar seguros de que es parte del dominio de\(f\).
La composición de funciones\(f\) y\(g\) está escrita\(f \cdot g\) y se define por
\((f \circ g)(x)=f(g(x))\)
Leemos\(f(g(x))\) a partir\(f\)\(g\) de\(x\).
De hecho, hemos usado la composición sin usar la notación muchas veces antes. Cuando graficamos funciones cuadráticas usando traducciones, estábamos componiendo funciones. Por ejemplo, si primero graficamos\(g(x)=x^{2}\) como una parábola y luego la desplazamos hacia abajo verticalmente cuatro unidades, estábamos usando la composición definida por\((f∘g)(x)=f(g(x))\) donde\(f(x)=x−4\).
Para funciones\(f(x)=4x-5\) y\(g(x)=2x+3\), encontrar
- \((f \circ g)(x)\)
- \((g \circ f)(x)\)
- \((f \cdot g)(x)\)
Solución:
-
Utilice la definición de\((f \circ g)(x)\). 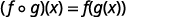

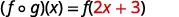

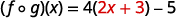
Distribuir. 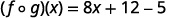
Simplificar. 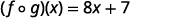
Cuadro 10.1.1 -
Utilice la definición de\((f \circ g)(x)\). 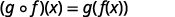

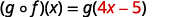

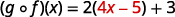
Distribuir. 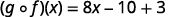
Simplificar. 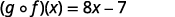
Cuadro 10.1.2
Observe la diferencia en el resultado en la parte a. y la parte b.
c. Aviso que\((f \cdot g)(x)\) es diferente a\((f \circ g)(x)\). En la parte a. hicimos la composición de las funciones. Ahora en la parte c. no los estamos componiendo, los estamos multiplicando.
Utilice la definición de\((f \cdot g)(x)\).
\((f \cdot g)(x)=f(x) \cdot g(x)\)
Sustituto\(f(x)=4 x-5\) y\(g(x)=2 x+3\).
\((f \cdot g)(x)=(4 x-5) \cdot(2 x+3)\)
Multiplicar.
\((f \cdot g)(x)=8 x^{2}+2 x-15\)
Para funciones\(f(x)=3x-2\) y\(g(x)=5x+1\), encontrar
- \((f \circ g)(x)\)
- \((g \circ f)(x)\)
- \((f \cdot g)(x)\)
- Contestar
-
- \(15x+1\)
- \(15x-9\)
- \(15 x^{2}-7 x-2\)
Para funciones\(f(x)=4 x-3\), y\(g(x)=6x-5\), encontrar
- \((f \circ g)(x)\)
- \((g \circ f)(x)\)
- \((f \cdot g)(x)\)
- Contestar
-
- \(24 x-23\)
- \(24 x-23\)
- \(24 x^{2}-38 x+15\)
En el siguiente ejemplo evaluaremos una composición para un valor específico.
Para funciones\(f(x)=x^{2}-4\), y\(g(x)=3 x+2\), encontrar:
- \((f \circ g)(-3)\)
- \((g \circ f)(-1)\)
- \((f \circ f)(2)\)
Solución:
-
Utilice la definición de\((f \circ g)(-3)\). 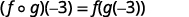

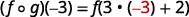
Simplificar. 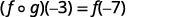

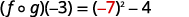
Simplificar. 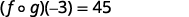
Cuadro 10.1.3 -
Utilice la definición de\((g \circ f)(-1)\). 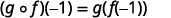

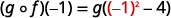
Simplificar. 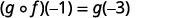

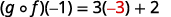
Simplificar. 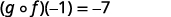
Cuadro 10.1.4 -
Utilice la definición de\((f \circ f)(2)\). 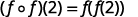

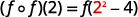
Simplificar. 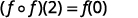

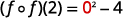
Simplificar. 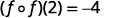
Cuadro 10.1.5
Para funciones\(f(x)=x^{2}-9\), y\(g(x)=2x+5\), encontrar
- \((f \circ g)(-2)\)
- \((g \circ f)(-3)\)
- \((f \circ f)(4)\)
- Contestar
-
- \(-8\)
- \(5\)
- \(40\)
Para funciones\(f(x)=x^{2}+1\), y\(g(x)=3x-5\), encontrar
- \((f \circ g)(-1)\)
- \((g \circ f)(2)\)
- \((f \circ f)(-1)\)
- Contestar
-
- \(65\)
- \(10\)
- \(5\)
Determine si una función es uno a uno
Cuando introdujimos funciones por primera vez, dijimos que una función es una relación que asigna a cada elemento en su dominio exactamente un elemento en el rango. Para cada par ordenado en la relación, cada\(x\) -valor se hace coincidir con un solo\(y\) -valor.
Usamos el ejemplo de cumpleaños para ayudarnos a entender la definición. Cada persona tiene un cumpleaños, pero nadie tiene dos cumpleaños y está bien que dos personas compartan un cumpleaños. Dado que cada persona tiene exactamente un cumpleaños, esa relación es una función.

Una función es uno a uno si cada valor en el rango tiene exactamente un elemento en el dominio. Por cada par ordenado en la función, cada valor y se hace coincidir con un solo\(x\) -valor.
Nuestro ejemplo de la relación de cumpleaños no es una función uno a uno. Dos personas pueden compartir el mismo cumpleaños. El valor de rango el 2 de agosto es el cumpleaños de Liz y junio, por lo que un valor de rango tiene dos valores de dominio. Por lo tanto, la función no es uno a uno.
Una función es uno a uno si cada valor en el rango corresponde a un elemento en el dominio. Para cada par ordenado en la función, cada\(y\) -valor se hace coincidir con un solo\(x\) -valor. No hay\(y\) valores repetidos.
Para cada conjunto de pares ordenados, determine si representa una función y, si es así, si la función es uno a uno.
- \(\{(-3,27),(-2,8),(-1,1),(0,0),(1,1),(2,8),(3,27)\}\)
- \(\{(0,0),(1,1),(4,2),(9,3),(16,4)\}\)
Solución:
- \(\{(-3,27),(-2,8),(-1,1),(0,0),(1,1),(2,8),(3,27)\}\)
Cada\(x\) valor -se corresponde con un solo\(y\) -valor. Entonces esta relación es una función.
Pero cada\(y\) -valor no está emparejado con un solo\(x\) -valor,\((−3,27)\) y\((3,27)\), por ejemplo. Entonces esta función no es uno-a-uno.
- \(\{(0,0),(1,1),(4,2),(9,3),(16,4)\}\)
Cada\(x\) valor -se corresponde con un solo\(y\) -valor. Entonces esta relación es una función.
Dado que cada\(y\) -valor está emparejado con un solo\(x\) -valor, esta función es uno a uno.
Para cada conjunto de pares ordenados, determine si representa una función y si es así, es la función uno a uno.
- \(\{(-3,-6),(-2,-4),(-1,-2),(0,0),(1,2),(2,4),(3,6)\}\)
- \(\{(-4,8),(-2,4),(-1,2),(0,0),(1,2),(2,4),(4,8)\}\)
- Contestar
-
- Función uno a uno
- Función; no uno a uno
Para cada conjunto de pares ordenados, determine si representa una función y si es así, es la función uno a uno.
- \(\{(27,-3),(8,-2),(1,-1),(0,0),(1,1),(8,2),(27,3)\}\)
- \(\{(7,-3),(-5,-4),(8,0),(0,0),(-6,4),(-2,2),(-1,3)\}\)
- Contestar
-
- No es una función
- Función; no uno a uno
Para ayudarnos a determinar si una relación es una función, utilizamos la prueba de línea vertical. Un conjunto de puntos en un sistema de coordenadas rectangulares es la gráfica de una función si cada línea vertical intersecta la gráfica en como máximo un punto. Además, si alguna línea vertical intersecta la gráfica en más de un punto, la gráfica no representa una función.
La línea vertical representa un\(x\) -value y comprobamos que intersecta la gráfica en un solo\(y\) -valor. Entonces es una función.
Para verificar si una función es uno a uno, utilizamos un proceso similar. Usamos una línea horizontal y verificamos que cada línea horizontal intersecta la gráfica en un solo punto. La línea horizontal representa un\(y\) -valor y comprobamos que intersecta la gráfica en un solo\(x\) -valor. Si cada línea horizontal intersecta la gráfica de una función como máximo en un punto, es una función uno a uno. Esta es la prueba de línea horizontal.
Prueba de Línea Horizontal
Si cada línea horizontal intersecta la gráfica de una función como máximo en un punto, es una función uno a uno.
Podemos probar si una gráfica de una relación es una función usando la prueba de línea vertical. Entonces podemos decir si la función es uno a uno aplicando la prueba de línea horizontal.
Determinar
- si cada gráfica es la gráfica de una función y, en caso afirmativo,
- si es uno a uno
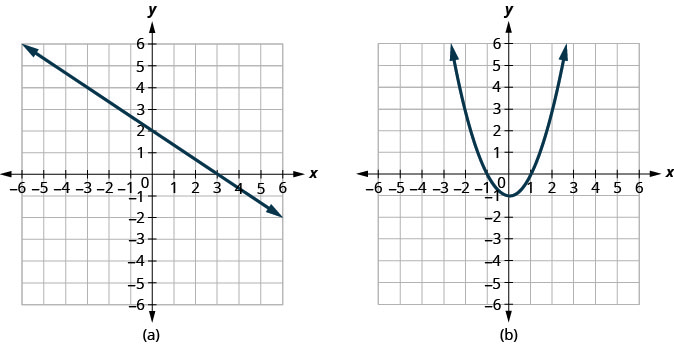
Solución:
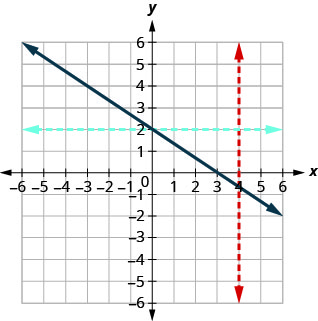
Figura 10.1.40
Dado que cualquier línea vertical intersecta la gráfica en como máximo un punto, la gráfica es la gráfica de una función. Dado que cualquier línea horizontal intersecta la gráfica como máximo en un punto, la gráfica es la gráfica de una función uno a uno.
b.
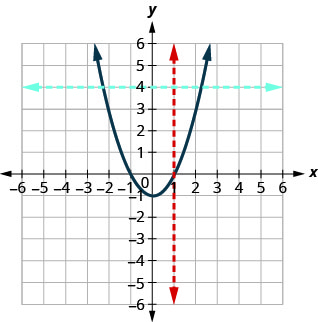
Dado que cualquier línea vertical intersecta la gráfica en como máximo un punto, la gráfica es la gráfica de una función. La línea horizontal que se muestra en la gráfica la cruza en dos puntos. Esta gráfica no representa una función uno a uno.
Determinar
- si cada gráfica es la gráfica de una función y, en caso afirmativo,
- si es uno a uno
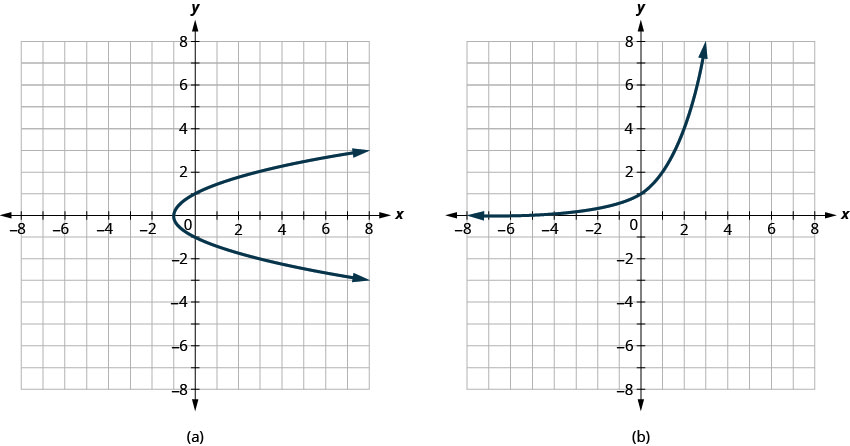
- Contestar
-
- No es una función
- Función uno a uno
Determinar
- si cada gráfica es la gráfica de una función y, en caso afirmativo,
- si es uno a uno
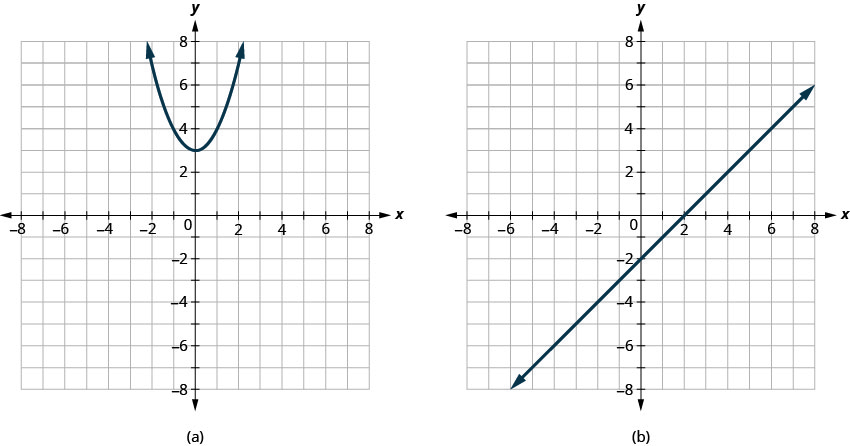
- Contestar
-
- Función; no uno a uno
- Función uno a uno
Encontrar la inversa de una función
Veamos una función uno a uno,\(f\), representada por los pares ordenados\(\{(0,5),(1,6),(2,7),(3,8)\}\). Por cada\(x\) -valor,\(f\) suma\(5\) para obtener el\(y\) -valor. Para 'deshacer' la suma de\(5\), restamos\(5\) de cada\(y\) -valor y volvemos al\(x\) valor -original. Podemos llamar a esto “tomando la inversa de\(f\)” y nombrar la función\(f^{−1}\).
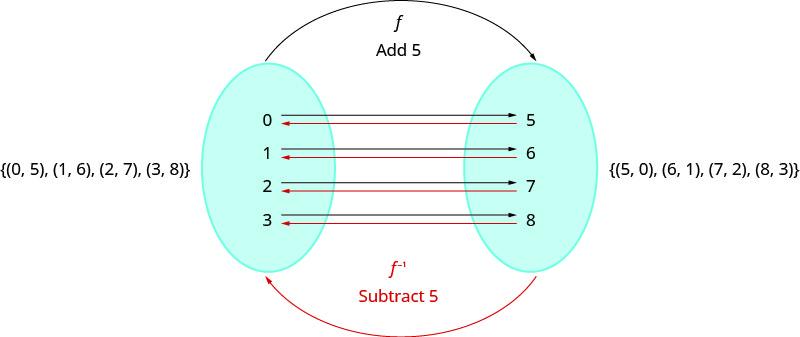
Observe que los pares ordenados de\(f\) y\(f^{−1}\) tienen sus\(x\) -valores y\(y\) -valores invertidos. El dominio de\(f\) es el rango de\(f^{−1}\) y el dominio de\(f^{−1}\) es el rango de\(f\).
Inverso de una función definida por pares ordenados
Si\(f(x)\) es una función uno a uno cuyos pares ordenados son de la forma\((x,y)\), entonces su función inversa\(f^{−1}(x)\) es el conjunto de pares ordenados\((y,x)\).
En el siguiente ejemplo encontraremos la inversa de una función definida por pares ordenados.
Encuentra la inversa de la función\(\{(0,3),(1,5),(2,7),(3,9)\}\). Determinar el dominio y el rango de la función inversa.
Solución:
Esta función es uno a uno ya que cada\(x\) -valor está emparejado con exactamente un\(y\) -valor.
Para encontrar la inversa invertimos los\(x\) -valores y\(y\) -valores en los pares ordenados de la función.
\(\begin{array}{ll} {\text{Function}}&{\{(0,3),(1,5),(2,7),(3,9)\}} \\ {\text{Inverse Function}}& {\{(3,0), (5,1), (7,2), (9,3)\}} \\ {\text{Domain of Inverse Function}}&{\{3, 5, 7, 9\}} \\ {\text{Range of Inverse Function}}&{\{0, 1, 2, 3\}} \end{array}\)
Encuentra la inversa de\(\{(0,4),(1,7),(2,10),(3,13)\}\). Determinar el dominio y el rango de la función inversa.
- Contestar
-
Función inversa:\(\{(4,0),(7,1),(10,2),(13,3)\}\). Dominio:\(\{4,7,10,13\}\). Rango:\(\{0,1,2,3\}\).
Encuentra la inversa de\(\{(-1,4),(-2,1),(-3,0),(-4,2)\}\). Determinar el dominio y el rango de la función inversa.
- Contestar
-
Función inversa:\(\{(4,-1),(1,-2),(0,-3),(2,-4)\}\). Dominio:\(\{0,1,2,4\}\). Rango:\(\{-4,-3,-2,-1\}\).
Acabamos de señalar que si\(f(x)\) es una función uno a uno cuyos pares ordenados son de la forma\((x,y)\), entonces su función inversa\(f^{−1}(x)\) es el conjunto de pares ordenados\((y,x)\).
Entonces, si un punto\((a,b)\) está en la gráfica de una función\(f(x)\), entonces el par ordenado\((b,a)\) está en la gráfica de\(f^{−1}(x)\). Ver Figura 10.1.43.
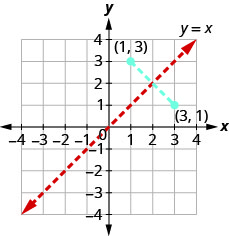
La distancia entre dos pares cualesquiera\((a,b)\) y\((b,a)\) se corta a la mitad por la línea\(y=x\). Entonces decimos que los puntos son imágenes especular entre sí a través de la línea\(y=x\).
Dado que cada punto en la gráfica de una función\(f(x)\) es una imagen especular de un punto en la gráfica de\(f^{−1}(x)\), decimos que las gráficas son imágenes especular entre sí a través de la línea\(y=x\). Utilizaremos este concepto para graficar la inversa de una función en el siguiente ejemplo.
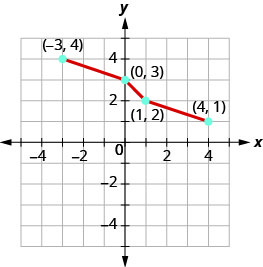
Gráfica, en el mismo sistema de coordenadas, la inversa de la función uno a uno que se muestra.
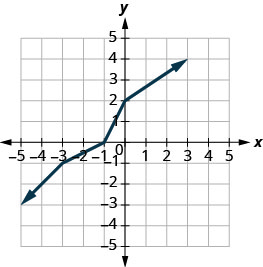
Solución:
Podemos usar puntos en la gráfica para encontrar puntos en la gráfica inversa. Algunos puntos en la gráfica son:\((−5,−3),(−3,−1),(−1,0),(0,2),(3,4)\).
Entonces, la función inversa contendrá los puntos:\((−3,−5),(−1,−3),(0,−1),(2,0),(4,3)\).
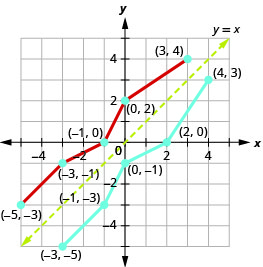
Observe cómo la gráfica de la función original y la gráfica de las funciones inversas son imágenes especulares a través de la línea\(y=x\).
Gráfica, en el mismo sistema de coordenadas, la inversa de la función uno a uno.
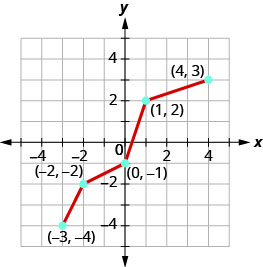
- Contestar
-
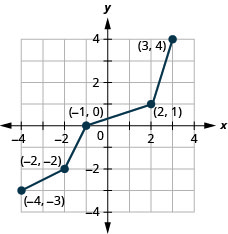
Figura 10.1.49
Gráfica, en el mismo sistema de coordenadas, la inversa de la función uno a uno.
- Contestar
-
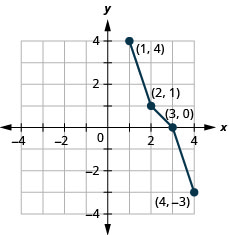
Figura 10.1.51
Cuando comenzamos nuestra discusión sobre una función inversa, hablamos sobre cómo la función inversa 'deshace' lo que la función original hizo a un valor en su dominio para volver al\(x\) valor original.

Funciones inversas
\(f^{-1}(f(x))=x\), para todos\(x\) en el dominio de\(f\)
\(f\left(f^{-1}(x)\right)=x\), para todos\(x\) en el dominio de\(f^{-1}\)
Podemos utilizar esta propiedad para verificar que dos funciones son inversas entre sí.
Verificar que\(f(x)=5x−1\) y\(g(x)=\frac{x+1}{5}\) son funciones inversas.
Solución:
Las funciones son inversas entre sí si\(g(f(x))=x\) y\(f(g(x))=x\).
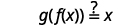 |
|
| Sustituir\(5x-1\) por\(f(x)\). | 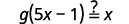 |
 |
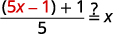 |
| Simplificar. | 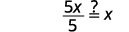 |
| Simplificar. | 
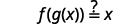
|
| Sustituto\(\frac{x+1}{5}\) de\(g(x)\). | 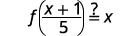 |
 |
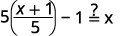 |
| Simplificar. | 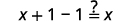 |
| Simplificar. |  |
Ya que ambos\(g(f(x))=x\) y\(f(g(x))=x\) son verdaderos, las funciones\(f(x)=5x−1\) y\(g(x)=\frac{x+1}{5}\) son funciones inversas. Es decir, son inversos el uno del otro.
Verificar que las funciones sean funciones inversas. \(f(x)=4 x-3\)y\(g(x)=\frac{x+3}{4}\).
- Contestar
-
\(g(f(x))=x\), y\(f(g(x))=x\), entonces son inversos.
Verificar que las funciones sean funciones inversas. \(f(x)=2 x+6\)y\(g(x)=\frac{x-6}{2}\)
- Contestar
-
\(g(f(x))=x,\)y\(f(g(x))=x,\) así son inversos.
Hemos encontrado inversos de función definidos por pares ordenados y a partir de una gráfica. Ahora veremos cómo encontrar una inversa usando una ecuación algebraica. El método utiliza la idea de que si\(f(x)\) es una función uno a uno con pares ordenados\((x,y)\), entonces su función inversa\(f^{−1}(x)\) es el conjunto de pares ordenados\((y,x)\).
Si invertimos el\(x\) y\(y\) en la función y luego resolvemos para\(y\), obtenemos nuestra función inversa.
Encuentra la inversa de\(f(x)=4 x+7\).
Solución:
| Paso 1. Sustituto\(y\) de\(f(x)\). | Reemplazar\(f(x)\) con\(y\). | \(\begin{aligned} f(x) &=4 x+7 \\ y &=4 x+7 \end{aligned}\) |
| Paso 2: Intercambiar las variables\(x\) y\(y\). | Reemplazar\(x\) con\(y\) y luego\(y\) con\(x\). | \(x=4y+7\) |
| Paso 3: Resolver para\(y\). |
Restar\(7\) de cada lado. Dividir por\(4\). |
\(x-7=4 y\) \(\frac{x-7}{4}=y\) |
| Paso 4: Sustituir\(f^{-1}(x)\) por\(y\). | Reemplazar\(y\) con\(f^{-1}(x)\). | \(\frac{x-7}{4}=f^{-1}(x)\) |
| Paso 5: Verificar que las funciones sean inversas. |
Mostrar\(f^{-1}(f(x))=x\) y\(f\left(f^{-1}(x)\right)=x\) |
\(\begin{aligned} f^{-1}(f(x)) & \stackrel{?}{=} x \\f^{-1}(4x+7)&\stackrel{?}{=}x\\ \frac{(4x+7)-7}{4}&\stackrel{?}{=}x \\ \frac{4x}{4}&\stackrel{?}{=}x\\x&=x \\ \\f(f^{-1}(x))&\stackrel{?}{=}x \\f \left(\frac{x-7}{4} \right)&\stackrel{?}{=}x \\ 4\left(\frac{x-7}{4} \right) + 7 &\stackrel{?}{=}x \\ x-7+7&\stackrel{?}{=}x \\x&=x \end{aligned}\) |
Encuentra la inversa de la función\(f(x)=5x-3\).
- Contestar
-
\(f^{-1}(x)=\frac{x+3}{5}\)
Encuentra la inversa de la función\(f(x)=8 x+5\).
- Contestar
-
\(f^{-1}(x)=\frac{x-5}{8}\)
Resumimos los pasos a continuación.
Cómo encontrar la inversa de una función uno a uno
- Sustituto\(y\) de\(f(x)\).
- Intercambiar las variables\(x\) y\(y\).
- Resolver para\(y\).
- Sustituto\(f^{−1}(x)\) de\(y\).
- Verifique que las funciones sean inversas.
Encuentra la inversa de\(f(x)=\sqrt[5]{2 x-3}\).
Solución:
\(f(x)=\sqrt[5]{2 x-3}\)
Sustituto\(y\) de\(f(x)\).
\(y=\sqrt[5]{2 x-3}\)
Intercambiar las variables\(x\) y\(y\).
\(x=\sqrt[5]{2 y-3}\)
Resolver para\(y\).
\(\begin{aligned}(x)^{5} &=(\sqrt[5]{2 y-3})^{5} \\ x^{5} &=2 y-3 \\ x^{5}+3 &=2 y \\ \frac{x^{5}+3}{2} &=y \end{aligned}\)
Sustituto\(f^{-1}(x)\) de\(y\).
\(f^{-1}(x)=\frac{x^{5}+3}{2}\)
Verifique que las funciones sean inversas.
\(\begin{array}{rr} {f^{-1}(f(x)) \stackrel{?}{=} x} & {f\left(f^{-1}(x)\right) \stackrel{?}{=} x} \\ {f^{-1}(\sqrt[5]{2x-3})\stackrel{?}{=}x}&{f\left(\frac{x^{5}+3}{2} \right)}\stackrel{?}{=}x \\ {\frac{(\sqrt[5]{2x-3})^{5}+3}{2}\stackrel{?}{=}x}&{\sqrt[5]{2\left(\frac{x^{5}+3}{2} \right)-3}\stackrel{?}{=}x} \\ {\frac{2x-3+3}{2}\stackrel{?}{=}x}&{\sqrt[5]{x^{5}+3-3}\stackrel{?}{=}x}\\ {\frac{2x}{2}\stackrel{?}{=}x}&{\sqrt[5]{x^{5}}\stackrel{?}{=}x} \\ {x=x}&{x=x} \end{array}\)
Encuentra la inversa de la función\(f(x)=\sqrt[5]{3 x-2}\).
- Contestar
-
\(f^{-1}(x)=\frac{x^{5}+2}{3}\)
Encuentra la inversa de la función\(f(x)=\sqrt[4]{6 x-7}\).
- Contestar
-
\(f^{-1}(x)=\frac{x^{4}+7}{6}\)
Conceptos clave
- Composición de Funciones: La composición de funciones\(f\) y\(g\), está escrita\(f∘g\) y está definida por
\((f \circ g)(x)=f(g(x))\)
Leemos\(f(g(x))\) a partir\(f\)\(g\) de\(x\). - Prueba de Línea Horizontal: Si cada línea horizontal, intersecta la gráfica de una función como máximo en un punto, es una función uno a uno.
- Inverso de una función definida por pares ordenados: Si\(f(x)\) es una función uno a uno cuyos pares ordenados son de la forma\((x,y)\), entonces su función inversa\(f^{−1}(x)\) es el conjunto de pares ordenados\((y,x)\).
- Funciones inversas: Para cada uno\(x\) en el dominio de la función uno-a-uno\(f\) y\(f^{−1}\),
\(f^{-1}(f(x))=x\)
\(f\left(f^{-1}(x)\right)=x\) - Cómo encontrar el inverso de una función uno a uno:
- Sustituto\(y\) de\(f(x)\).
- Intercambiar las variables\(x\) y\(y\).
- Resolver para\(y\).
- Sustituto\(f^{−1}(x)\) de\(y\).
- Verifique que las funciones sean inversas.
Glosario
- función uno-a-uno
- Una función es uno a uno si cada valor en el rango tiene exactamente un elemento en el dominio. Para cada par ordenado en la función, cada\(y\) -valor se hace coincidir con un solo\(x\) -valor.


