10.3E: Ejercicios
- Page ID
- 112554
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
La práctica hace la perfección
En los siguientes ejercicios, grafica cada función exponencial.
- \(f(x)=2^{x}\)
- \(g(x)=3^{x}\)
- \(f(x)=6^{x}\)
- \(g(x)=7^{x}\)
- \(f(x)=(1.5)^{x}\)
- \(g(x)=(2.5)^{x}\)
- \(f(x)=\left(\frac{1}{2}\right)^{x}\)
- \(g(x)=\left(\frac{1}{3}\right)^{x}\)
- \(f(x)=\left(\frac{1}{6}\right)^{x}\)
- \(g(x)=\left(\frac{1}{7}\right)^{x}\)
- \(f(x)=(0.4)^{x}\)
- \(g(x)=(0.6)^{x}\)
- Contestar
-
1.
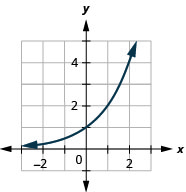
Figura 10.2.22 3.
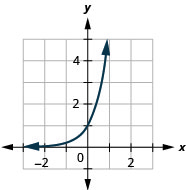
Figura 10.2.23 5.
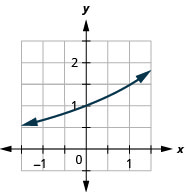
Figura 10.2.24 7.
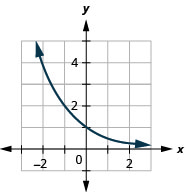
Figura 10.2.25 9.
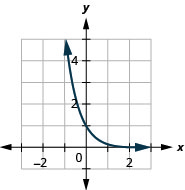
Figura 10.2.26 11.
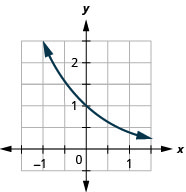
Figura 10.2.27
En los siguientes ejercicios, grafica cada función en un mismo sistema de coordenadas.
- \(f(x)=4^{x}, g(x)=4^{x-1}\)
- \(f(x)=3^{x}, g(x)=3^{x-1}\)
- \(f(x)=2^{x}, g(x)=2^{x-2}\)
- \(f(x)=2^{x}, g(x)=2^{x+2}\)
- \(f(x)=3^{x}, g(x)=3^{x}+2\)
- \(f(x)=4^{x}, g(x)=4^{x}+2\)
- \(f(x)=2^{x}, g(x)=2^{x}+1\)
- \(f(x)=2^{x}, g(x)=2^{x}-1\)
- Contestar
-
1.
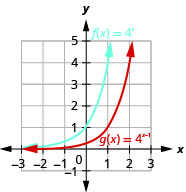
Figura 10.2.28 3.
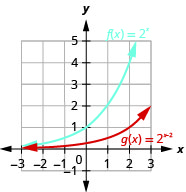
Figura 10.2.29 5.
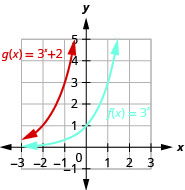
Figura 10.2.30 7.
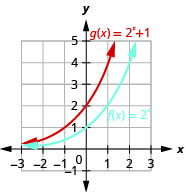
Figura 10.2.31
En los siguientes ejercicios, grafica cada función exponencial.
- \(f(x)=3^{x+2}\)
- \(f(x)=3^{x-2}\)
- \(f(x)=2^{x}+3\)
- \(f(x)=2^{x}-3\)
- \(f(x)=\left(\frac{1}{2}\right)^{x-4}\)
- \(f(x)=\left(\frac{1}{2}\right)^{x}-3\)
- \(f(x)=e^{x}+1\)
- \(f(x)=e^{x-2}\)
- \(f(x)=-2^{x}\)
- \(f(x)=2^{-x-1}-1\)
- Contestar
-
1.
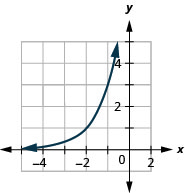
Figura 10.2.32 3.
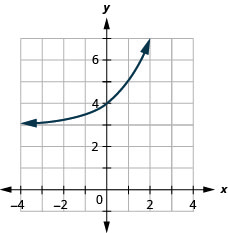
Figura 10.2.33 5.
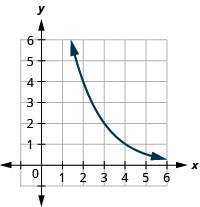
Figura 10.2.34 7.
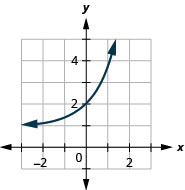
Figura 10.2.35 9.
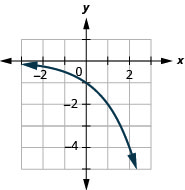
Figura 10.2.36
En los siguientes ejercicios, resuelve cada ecuación.
- \(2^{3 x-8}=16\)
- \(2^{2 x-3}=32\)
- \(3^{x+3}=9\)
- \(3^{x^{2}}=81\)
- \(4^{x^{2}}=4\)
- \(4^{x}=32\)
- \(4^{x+2}=64\)
- \(4^{x+3}=16\)
- \(2^{x^{2}+2 x}=\frac{1}{2}\)
- \(3^{x^{2}-2 x}=\frac{1}{3}\)
- \(e^{3 x} \cdot e^{4}=e^{10}\)
- \(e^{2 x} \cdot e^{3}=e^{9}\)
- \(\frac{e^{x^{2}}}{e^{2}}=e^{x}\)
- \(\frac{e^{x^{2}}}{e^{3}}=e^{2 x}\)
- Contestar
-
1. \(x=4\)
3. \(x=-1\)
5. \(x=-1, x=1\)
7. \(x=1\)
9. \(x=-1\)
11. \(x=2\)
13. \(x=-1, x=2\)
En los siguientes ejercicios, haga coincidir las gráficas con una de las siguientes funciones:
- \(2^{x}\)
- \(2^{x+1}\)
- \(2^{x-1}\)
- \(2^{x}+2\)
- \(2^{x}-2\)
- \(3^{x}\)
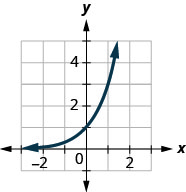
Figura 10.2.37
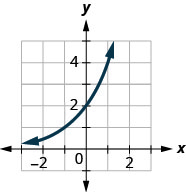
Figura 10.2.38
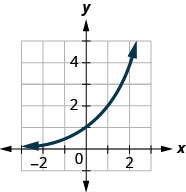
Figura 10.2.39
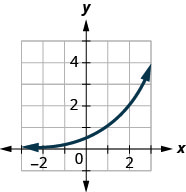
Figura 10.2.40
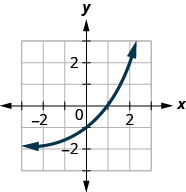
Figura 10.2.41
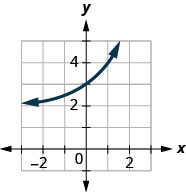
Figura 10.2.42
- Contestar
-
1. f
3. a
5. e
En los siguientes ejercicios, utilizar un modelo exponencial para resolver.
- Edgar acumuló $\(5,000\) en deuda de tarjetas de crédito. Si la tasa de interés es\(20\)% anual, y no realiza ningún pago por\(2\) años, ¿cuánto deberá sobre esta deuda en\(2\) años por cada método de composición?
- compuesto trimestral
- compuesto mensual
- compuesto continuamente
- Cynthia invirtió $\(12,000\) en una cuenta de ahorros. Si la tasa de interés es\(6\)%, ¿cuánto habrá en la cuenta en\(10\) años por cada método de composición?
- compuesto trimestral
- compuesto mensual
- compuesto continuamente
- Rochelle deposita $\(5,000\) en una IRA. ¿Cuál será el valor de su inversión en\(25\) años si la inversión está ganando\(8\)% anual y se complica continuamente?
- Nazerhy deposita $\(8,000\) en un certificado de depósito. La tasa de interés anual es\(6\)% y el interés se computará trimestralmente. ¿Cuánto valdrá el certificado en\(10\) años?
- Un investigador del Centro para el Control y la Prevención de Enfermedades está estudiando el crecimiento de una bacteria. Comienza su experimento con\(100\) de la bacteria que crece a una tasa de\(6\)% por hora. Él revisará la bacteria cada\(8\) hora. ¿Cuántas bacterias encontrará en\(8\) horas?
- Un biólogo está observando el patrón de crecimiento de un virus. Comienza con\(50\) del virus que crece a una tasa de\(20\)% por hora. Ella revisará el virus en\(24\) horas. ¿Cuántos virus va a encontrar?
- En los últimos diez años la población de Indonesia ha crecido a una tasa de\(1.12\)% anual a\(258,316,051\). Si esta tasa continúa, ¿cuál será la población en\(10\) más años?
- En los últimos diez años la población de Brasil ha crecido a una tasa de\(0.9\)% anual a\(205,823,665\). Si esta tasa continúa, ¿cuál será la población en\(10\) más años?
- Contestar
-
1.
- $\(7,387.28\)
- $\(7,434.57\)
- $\(7,459.12\)
3. $\(36,945.28\)
5. \(223\)bacterias
7. \(288,929,825\)
- Explica cómo puedes distinguir entre funciones exponenciales y funciones polinómicas.
- Comparar y contrastar las gráficas de\(y=x^{2}\) y\(y=2^{x}\).
- ¿Qué sucede con una función exponencial como los valores de las\(x\) disminuciones? ¿Alguna vez la gráfica cruzará el\(x\) eje -eje? Explique.
- Contestar
-
1. Las respuestas variarán
3. Las respuestas variarán
Autocomprobación
a. después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.
b. Después de revisar esta lista de verificación, ¿qué harás para tener confianza en todos los objetivos?