11.2: Fórmulas y círculos de distancia y punto medio
- Page ID
- 112788
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Al final de esta sección, podrás:
- Usa la Fórmula de Distancia
- Utilice la fórmula de punto medio
- Escribir la ecuación de un círculo en forma estándar
- Graficar un círculo
Antes de comenzar, toma este cuestionario de preparación.
- Encuentra la longitud de la hipotenusa de un triángulo rectángulo cuyas patas son\(12\) y\(16\) pulgadas.
Si te perdiste este problema, revisa el Ejemplo 2.34. - Factor:\(x^{2}-18 x+81\).
Si te perdiste este problema, revisa el Ejemplo 6.24. - Resuelve completando la plaza:\(x^{2}-12 x-12=0\).
Si te perdiste este problema, revisa el Ejemplo 9.22.
En este capítulo veremos las secciones cónicas, generalmente llamadas las cónicas, y sus propiedades. Las cónicas son curvas que resultan de un plano que interseca un cono doble, dos conos colocados punto a punto. Cada mitad de un cono doble se llama nappe.
Hay cuatro cónicas: el círculo, la parábola, la elipse y la hipérbola. La siguiente figura muestra cómo el plano que interseca el doble cono resulta en cada curva.
Cada una de las curvas tiene muchas aplicaciones que afectan tu vida diaria, desde tu celular hasta sistemas acústicos y de navegación. En esta sección veremos las propiedades de un círculo.
Usa la Fórmula de Distancia
Hemos utilizado el Teorema de Pitágoras para encontrar las longitudes de los lados de un triángulo rectángulo. Aquí volveremos a utilizar este teorema para encontrar distancias en el sistema de coordenadas rectangulares. Al encontrar la distancia en el sistema de coordenadas rectangulares, podemos establecer una conexión entre la geometría de una cónica y el álgebra, lo que abre un mundo de oportunidades de aplicación.
Nuestro primer paso es desarrollar una fórmula para encontrar distancias entre puntos en el sistema de coordenadas rectangulares. Trazaremos los puntos y crearemos un triángulo rectángulo tanto como lo hicimos cuando encontramos pendiente en Gráficas y Funciones. Luego damos un paso más allá y usamos el Teorema de Pitágoras para encontrar la longitud de la hipotenusa del triángulo, que es la distancia entre los puntos.
Utilice el sistema de coordenadas rectangulares para encontrar la distancia entre los puntos\((6,4)\) y\((2,1)\).
Solución
| Trazar los dos puntos. Conecta los dos puntos con una línea. Dibuja un triángulo rectángulo como si fueras a encontrar pendiente. |
|
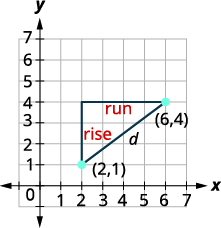
| Encuentra la longitud de cada pierna. |
|
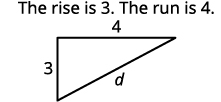
| Usa el Teorema de Pitágoras para encontrar\(d\), la distancia entre los dos puntos. | \(a^{2}+b^{2}=c^{2}\) |
| Sustituto en los valores. | \(3^{2}+4^{2}=d^{2}\) |
| Simplificar. | \(9+16=d^{2}\) |
| \(25=d^{2}\) | |
| Utilice la Propiedad Raíz Cuadrada. | \(d=5\quad\cancel{d=-5}\) |
| Ya que la distancia,\(d\) es positiva, podemos eliminar\(d=-5\). | La distancia entre los puntos\((6,4)\) y\((2,1)\) es\(5\). |
Utilice el sistema de coordenadas rectangulares para encontrar la distancia entre los puntos\((6,1)\) y\((2,-2)\).
- Contestar
-
\(d=5\)
Utilice el sistema de coordenadas rectangulares para encontrar la distancia entre los puntos\((5,3)\) y\((-3,-3)\).
- Contestar
-
\(d=10\)
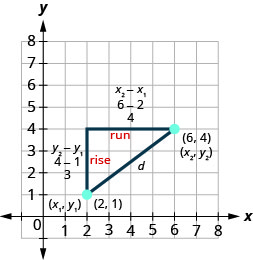
El método que utilizamos en el último ejemplo nos lleva a la fórmula para encontrar la distancia entre los dos puntos\(\left(x_{1}, y_{1}\right)\) y\(\left(x_{2}, y_{2}\right)\).
Cuando encontramos la longitud de la pata horizontal restamos\(6−2\) que es\(x_{2}-x_{1}\).
Cuando encontramos la longitud de la pata vertical restamos\(4−1\) cual es\(y_{2}-y_{1}\).
Si el triángulo hubiera estado en una posición diferente, es posible que hayamos restado\(x_{1}-x_{2}\) o\(y_{1}-y_{2}\). Las expresiones\(x_{2}-x_{1}\) y\(x_{1}-x_{2}\) varían sólo en el signo del número resultante. Para obtener el valor positivo -ya que la distancia es positiva- podemos usar el valor absoluto. Entonces para generalizar diremos\(\left|x_{2}-x_{1}\right|\) y\(\left|y_{2}-y_{1}\right|\).
En el Teorema de Pitágoras, sustituimos las expresiones generales\(\left|x_{2}-x_{1}\right|\) y\(\left|y_{2}-y_{1}\right|\) más que los números.
\(\begin{array}{l c}{} & {a^{2}+b^{2}=c^{2}} \\ {\text {Substitute in the values. }}&{(|x_{2}-x_{1}|)^{2}+(|y_{2}-y_{1}|)^{2}=d^{2}} \\ {\text{Squaring the expressions makes}}&{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}=d^{2}} \\ \text{them positive, so we eliminate} \\\text{the absolute value bars.}\\ {\text{Use the Square Root Property.}}&{d=\pm\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}\\ {\text{Distance is positive, so eliminate}}&{d=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}\\\text{the negative value.}\end{array}\)
Esta es la Fórmula de Distancia que utilizamos para encontrar la distancia\(d\) entre los dos puntos\((x_{1},y_{1})\) y\((x_{2}, y_{2})\).
Fórmula de distancia
La distancia\(d\) entre los dos puntos\((x_{1},y_{1})\) y\((x_{2}, y_{2})\) es
\(d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
Usa la Fórmula de Distancia para encontrar la distancia entre los puntos\((-5,-3)\) y\((7,2)\).
Solución:
Escribe la Fórmula de Distancia.
\(d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
Etiquete los puntos,\(\left( \begin{array}{c}{x_{1}, y_{1}} \\ {-5,-3}\end{array}\right)\),\(\left( \begin{array}{l}{x_{2}, y_{2}} \\ {7,2}\end{array}\right)\) y sustituya.
\(d=\sqrt{(7-(-5))^{2}+(2-(-3))^{2}}\)
Simplificar.
\(d=\sqrt{12^{2}+5^{2}}\)
\(d=\sqrt{144+25}\)
\(d=\sqrt{169}\)
\(d=13\)
Respuesta:
\(d=13\)
Usa la Fórmula de Distancia para encontrar la distancia entre los puntos\((-4,-5)\) y\((5,7)\).
- Contestar
-
\(d=15\)
Usa la Fórmula de Distancia para encontrar la distancia entre los puntos\((-2,-5)\) y\((-14,-10)\).
- Contestar
-
\(d=13\)
Usa la Fórmula de Distancia para encontrar la distancia entre los puntos\((10,−4)\) y\((−1,5)\). Escribe la respuesta en forma exacta y luego encuentra la aproximación decimal, redondeada a la décima más cercana si es necesario.
Solución:
Escribe la Fórmula de Distancia.
\(d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
Etiquete los puntos,\(\left( \begin{array}{c}{x_{1}, y_{1}} \\ {10,-4}\end{array}\right)\),\(\left( \begin{array}{c}{x_{2}, y_{2}} \\ {-1,5}\end{array}\right)\) y sustituya.
\(d=\sqrt{(-1-10)^{2}+(5-(-4))^{2}}\)
Simplificar.
\(d=\sqrt{(-11)^{2}+9^{2}}\)
\(d=\sqrt{121+81}\)
\(d=\sqrt{202}\)
Como no\(202\) es un cuadrado perfecto, podemos dejar la respuesta en forma exacta o encontrar una aproximación decimal.
\(d=\sqrt{202}\)
o
\(d \approx 14.2\)
Usa la Fórmula de Distancia para encontrar la distancia entre los puntos\((−4,−5)\) y\((3,4)\). Escribe la respuesta en forma exacta y luego encuentra la aproximación decimal, redondeada a la décima más cercana si es necesario.
- Contestar
-
\(d=\sqrt{130}, d \approx 11.4\)
Usa la Fórmula de Distancia para encontrar la distancia entre los puntos\((−2,−5)\) y\((−3,−4)\). Escribe la respuesta en forma exacta y luego encuentra la aproximación decimal, redondeada a la décima más cercana si es necesario.
- Contestar
-
\(d=\sqrt{2}, d \approx 1.4\)
Utilice la fórmula de punto medio
A menudo es útil poder encontrar el punto medio de un segmento. Por ejemplo, si tiene los extremos del diámetro de un círculo, es posible que desee encontrar el centro del círculo que es el punto medio del diámetro. Para encontrar el punto medio de un segmento de línea, encontramos el promedio\(x\) de las coordenadas y el promedio\(y\) de las coordenadas de los puntos finales.
Fórmula de punto medio
El punto medio del segmento de línea cuyos extremos son los dos puntos\(\left(x_{1}, y_{1}\right)\) y\(\left(x_{2}, y_{2}\right)\) es
\(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\)
Para encontrar el punto medio de un segmento de línea, encontramos el promedio\(x\) de las coordenadas y el promedio\(y\) de las coordenadas de los puntos finales.
Utilice la Fórmula de punto medio para encontrar el punto medio de los segmentos de línea cuyos extremos son\((−5,−4)\) y\((7,2)\). Trazar los puntos finales y el punto medio en un sistema de coordenadas rectangulares.
Solución:
| Escribe la Fórmula de Punto Medio. | \(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\) |
| Etiquete los puntos\(\left( \begin{array}{c}{x_{1}, y_{1}} \\ {-5,-4}\end{array}\right), \left( \begin{array}{l}{x_{2}, y_{2}} \\ {7,2}\end{array}\right)\) y sustituya. | \(\left(\frac{-5+7}{2}, \frac{-4+2}{2}\right)\) |
| Simplificar. | \(\left(\frac{2}{2}, \frac{-2}{2}\right)\) |
|
\((1,-1)\) El punto medio del segmento es el punto \((1,-1)\). |
|
| Trazar los puntos finales y el punto medio. |
|
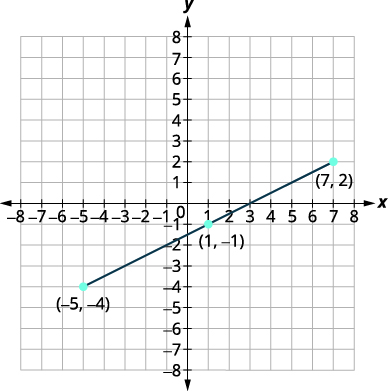
Utilice la Fórmula de punto medio para encontrar el punto medio de los segmentos de línea cuyos extremos son\((−3,−5)\) y\((5,7)\). Trazar los puntos finales y el punto medio en un sistema de coordenadas rectangulares.
- Contestar
-
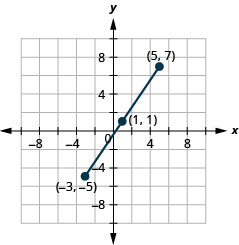
Figura 11.1.7
Utilice la Fórmula de punto medio para encontrar el punto medio de los segmentos de línea cuyos extremos son\((−2,−5)\) y\((6,−1)\). Trazar los puntos finales y el punto medio en un sistema de coordenadas rectangulares.
- Contestar
-
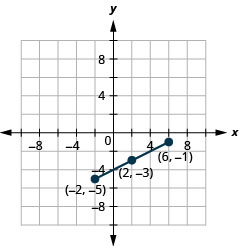
Figura 11.1.8
Tanto la Fórmula de Distancia como la Fórmula de Punto Medio dependen de dos puntos,\(\left(x_{1}, y_{1}\right)\) y\(\left(x_{2}, y_{2}\right)\). Es fácil confundir qué fórmula requiere suma y qué resta de las coordenadas. Si recordamos de dónde vienen las fórmulas, puede ser más fácil recordar las fórmulas.
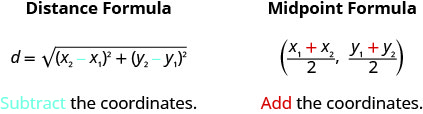
Escribir la Ecuación de un Círculo en Forma Estándar
Como mencionamos, nuestro objetivo es conectar la geometría de una cónica con el álgebra. Al usar el plano de coordenadas, podemos hacer esto fácilmente.
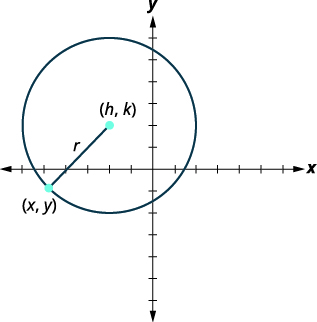
Definimos un círculo como todos los puntos en un plano que están a una distancia fija desde un punto dado en el plano. El punto dado se llama el centro,\((h,k)\), y la distancia fija se llama el radio\(r\),, del círculo.
Un círculo son todos los puntos en un plano que están a una distancia fija de un punto dado en el plano. El punto dado se llama el centro,\((h,k)\), y la distancia fija se llama el radio\(r\),, del círculo.
Observamos un círculo en el sistema de coordenadas rectangulares. El radio es la distancia desde el centro,\((h,k)\), a un punto en el círculo,\((x,y)\). |
|
| Para derivar la ecuación de un círculo, podemos usar la fórmula de distancia con los puntos\((h,k)\),\((x,y)\) y la distancia,\(r\). |
\(d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\) |
| Sustituir los valores. | \(r=\sqrt{(x-h)^{2}+(y-k)^{2}}\) |
| Cuadrado a ambos lados. | \(r^{2}=(x-h)^{2}+(y-k)^{2}\) |
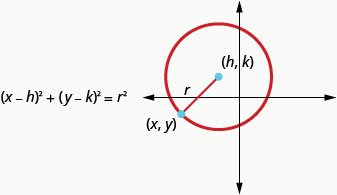
Esta es la forma estándar de la ecuación de un círculo con centro,\((h,k)\), y radio,\(r\).
La forma estándar de la ecuación de un círculo con centro\((h,k)\), y radio,\(r\), es
Escribe la forma estándar de la ecuación del círculo con radio\(3\) y centro\((0,0)\).
Solución:
| Usar la forma estándar de la ecuación de un círculo | \((x-h)^{2}+(y-k)^{2}=r^{2}\) |
| Sustituir en los valores\(r=3, h=0\), y\(k=0\). | \((x-0)^{2}+(y-0)^{2}=3^{2}\) |
 |
|
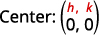| Simplificar. | \(x^{2}+y^{2}=9\) |
Escribe la forma estándar de la ecuación del círculo con un radio de\(6\) y centro\((0,0)\).
- Contestar
-
\(x^{2}+y^{2}=36\)
Escribe la forma estándar de la ecuación del círculo con un radio de\(8\) y centro\((0,0)\).
- Contestar
-
\(x^{2}+y^{2}=64\)
En el último ejemplo, el centro fue\((0,0)\). Observe lo que pasó con la ecuación. Siempre que el centro está\((0,0)\), la forma estándar se convierte\(x^{2}+y^{2}=r^{2}\).
Escribe la forma estándar de la ecuación del círculo con radio\(2\) y centro\((−1,3)\).
Solución:
| Utilice la forma estándar de la ecuación de un círculo. | \((x-h)^{2}+(y-k)^{2}=r^{2}\) |
| Sustituto en los valores. | \((x-(-1))^{2}+(y-3)^{2}=2^{2}\) |
 |
|
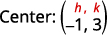| Simplificar. | \((x+1)^{2}+(y-3)^{2}=4\) |
Escribe la forma estándar de la ecuación del círculo con un radio de\(7\) y centro\((2,−4)\).
- Contestar
-
\((x-2)^{2}+(y+4)^{2}=49\)
Escribe la forma estándar de la ecuación del círculo con un radio de\(9\) y centro\((−3,−5)\).
- Contestar
-
\((x+3)^{2}+(y+5)^{2}=81\)
En el siguiente ejemplo, no se da el radio. Para calcular el radio, utilizamos la Fórmula de Distancia con los dos puntos dados.
Escribe la forma estándar de la ecuación del círculo con centro\((2,4)\) que también contiene el punto\((−2,1)\).
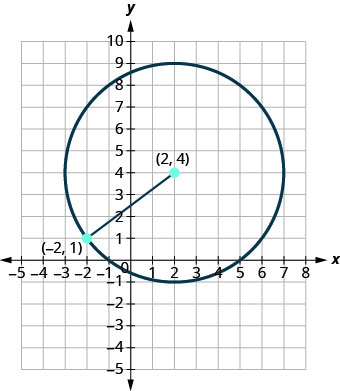
Solución:
El radio es la distancia desde el centro a cualquier punto del círculo para que podamos usar la fórmula de distancia para calcularlo. Usaremos el centro\((2,4)\) y el punto\((−2,1)\)
Usa la Fórmula de Distancia para encontrar el radio.
\(r=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
Sustituir los valores. \(\left( \begin{array}{l}{x_{1}, y_{1}} \\ {2,4}\end{array}\right), \left( \begin{array}{c}{x_{2}, y_{2}} \\ {-2,1}\end{array}\right)\)
\(r=\sqrt{(-2-2)^{2}+(1-4)^{2}}\)
Simplificar.
\(r=\sqrt{(-4)^{2}+(-3)^{2}}\)
\(r=\sqrt{16+9}\)
\(r=\sqrt{25}\)
\(r=5\)
Ahora que conocemos el radio,\(r=5\), y el centro,\((2,4)\), podemos usar la forma estándar de la ecuación de un círculo para encontrar la ecuación.
Utilice la forma estándar de la ecuación de un círculo.
\((x-h)^{2}+(y-k)^{2}=r^{2}\)
Sustituto en los valores.
\((x-2)^{2}+(y-4)^{2}=5^{2}\)
Simplificar.
\((x-2)^{2}+(y-4)^{2}=25\)
Escribe la forma estándar de la ecuación del círculo con centro\((2,1)\) que también contiene el punto\((−2,−2)\).
- Contestar
-
\((x-2)^{2}+(y-1)^{2}=25\)
Escribe la forma estándar de la ecuación del círculo con centro\((7,1)\) que también contiene el punto\((−1,−5)\).
- Contestar
-
\((x-7)^{2}+(y-1)^{2}=100\)
Graficar un círculo
Cualquier ecuación de la forma\((x-h)^{2}+(y-k)^{2}=r^{2}\) es la forma estándar de la ecuación de un círculo con centro,\((h,k)\), y radio,\(r\). Luego podemos graficar el círculo en un sistema de coordenadas rectangulares.
Tenga en cuenta que el formulario estándar requiere sustracción de\(x\) y\(y\). En el siguiente ejemplo, la ecuación tiene\(x+2\), por lo que necesitamos reescribir la suma como resta de un negativo.
Encuentra el centro y el radio, luego grafica el círculo:\((x+2)^{2}+(y-1)^{2}=9\).
Solución:
 |
|
|
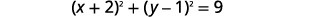Utilice la forma estándar de la ecuación de un círculo. Identificar el centro,\((h,k)\) y el radio,\(r\). |
 |
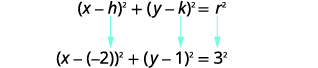| Centro:\((-2,1)\) radio:\(3\) | |
| Grafica el círculo. |  |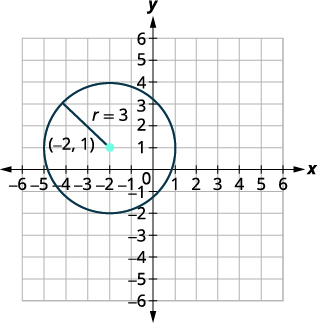
- Encuentra el centro y el radio, luego
- Grafica el círculo:\((x-3)^{2}+(y+4)^{2}=4\).
- Contestar
-
- El círculo está centrado en\((3,-4)\) con un radio de\(2\).
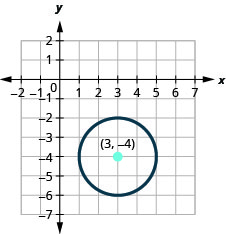
Figura 11.1.19
- Encuentra el centro y el radio, luego
- Grafica el círculo:\((x-3)^{2}+(y-1)^{2}=16\).
- Contestar
-
- El círculo está centrado en\((3,1)\) con un radio de\(4\).
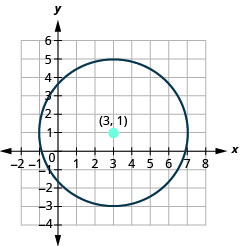
Figura 11.1.20
Para encontrar el centro y el radio, debemos escribir la ecuación en forma estándar. En el siguiente ejemplo, primero debemos obtener el coeficiente de\(x^{2}, y^{2}\) ser uno.
Encuentra el centro y el radio y luego grafica el círculo,\(4 x^{2}+4 y^{2}=64\).
Solución:
 |
|
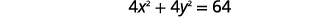| Dividir cada lado por\(4\). |  |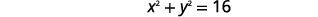
| Utilice la forma estándar de la ecuación de un círculo. Identificar el centro,\((h,k)\) y el radio,\(r\). |
 |
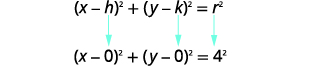| Centro:\((0,0)\) radio:\(4\) | |
| Grafica el círculo. |  |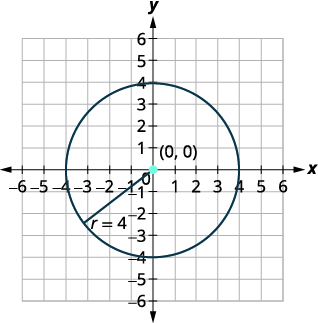
- Encuentra el centro y el radio, luego
- Grafica el círculo:\(3 x^{2}+3 y^{2}=27\)
- Contestar
-
- El círculo está centrado en\((0,0)\) con un radio de\(3\).
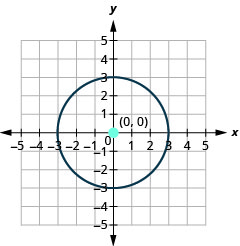
Figura 11.1.25
- Encuentra el centro y el radio, luego
- Grafica el círculo:\(5 x^{2}+5 y^{2}=125\)
- Contestar
-
- El círculo está centrado en\((0,0)\) con un radio de\(5\).
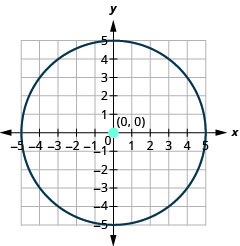
Figura 11.1.26
Si ampliamos la ecuación del Ejemplo 11.1.8,\((x+2)^{2}+(y-1)^{2}=9\), la ecuación del círculo se ve muy diferente.
\((x+2)^{2}+(y-1)^{2}=9\)
Cuadrar los binomios.
\(x^{2}+4 x+4+y^{2}-2 y+1=9\)
Organice los términos en orden descendente de grados y obtenga cero a la derecha
\(x^{2}+y^{2}+4 x-2 y-4=0\)
Esta forma de la ecuación se llama la forma general de la ecuación del círculo.
La forma general de la ecuación de un círculo es
\(x^{2}+y^{2}+a x+b y+c=0\)
Si se nos da una ecuación en forma general, podemos cambiarla a forma estándar completando los cuadrados en ambos\(x\) y\(y\). Entonces podemos graficar el círculo usando su centro y radio.
- Encuentra el centro y el radio, luego
- Grafica el círculo:\(x^{2}+y^{2}-4 x-6 y+4=0\)
Solución:
Necesitamos reescribir esta forma general en forma estándar para encontrar el centro y el radio.
|
|
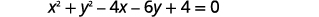
| Agrupe los\(x\) -términos y\(y\) -términos. Recoge las constantes en el lado derecho. |
|
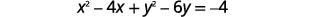
| Completa los cuadrados. |
|
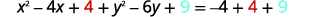
| Reescribir como cuadrados binomiales. |
|
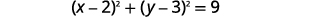
| Identificar el centro y el radio. | Centro:\((2,3)\) radio:\(3\) |
| Grafica el círculo. |
|
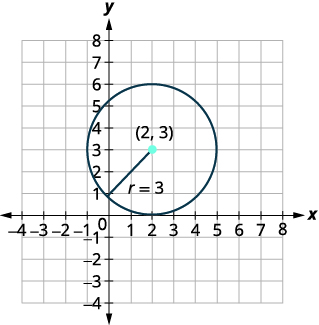
- Encuentra el centro y el radio, luego
- Grafica el círculo:\(x^{2}+y^{2}-6 x-8 y+9=0\).
- Contestar
-
- El círculo está centrado en\((3,4)\) con un radio de\(4\).
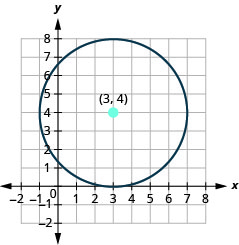
Figura 11.1.32
- Encuentra el centro y el radio, luego
- Grafica el círculo:\(x^{2}+y^{2}+6 x-2 y+1=0\)
- Contestar
-
- El círculo está centrado en\((-3,1)\) con un radio de\(3\).
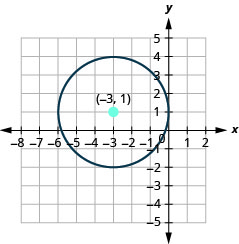
Figura 11.1.33
En el siguiente ejemplo, hay un\(y\) -término y un\(y^{2}\) -término. Pero fíjense que no hay\(x\) -término, sólo un\(x^{2}\) -término. Esto lo hemos visto antes y sabemos que significa que\(h\) es\(0\). Tendremos que completar el cuadrado para los\(y\) términos, pero no para los\(x\) términos.
- Encuentra el centro y el radio, luego
- Grafica el círculo:\(x^{2}+y^{2}+8 y=0\)
Solución:
Necesitamos reescribir esta forma general en forma estándar para encontrar el centro y el radio.
 |
|
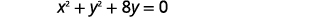| Agrupe los\(x\) -términos y\(y\) -términos. |  |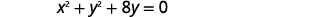
| No hay constantes que recoger en el lado derecho. | |
| Completa el cuadrado para\(y^{2}+8y\). |  |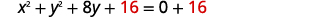
| Reescribir como cuadrados binomiales. |  |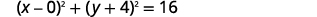
| Identificar el centro y el radio. | Centro:\((0,-4)\) radio:\(4\) |
| Grafica el círculo. |  |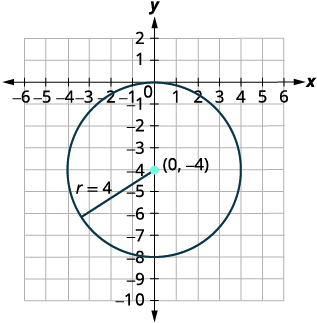
- Encuentra el centro y el radio, luego
- Grafica el círculo:\(x^{2}+y^{2}-2 x-3=0\).
- Contestar
-
- El círculo está centrado en\((-1,0)\) con un radio de\(2\).
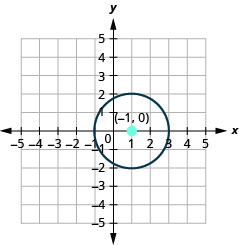
Figura 11.1.39
- Encuentra el centro y el radio, luego
- Grafica el círculo:\(x^{2}+y^{2}-12 y+11=0\).
- Contestar
-
- El círculo está centrado en\((0,6)\) con un radio de\(5\).
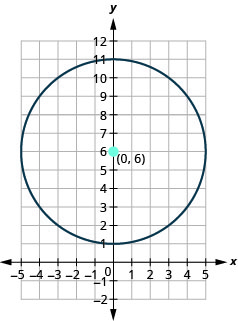
Figura 11.1.40
Acceda a estos recursos en línea para obtener instrucciones adicionales y practique con el uso de las fórmulas de distancia y punto medio, y graficando círculos.
- Fórmulas y círculos de distancia-punto medio
- Encontrar la distancia y el punto medio entre dos puntos
- Completar la ecuación de Cuadrado para Escribir en Forma Estándar de un Círculo
Conceptos clave
- Fórmula de distancia: La distancia\(d\) entre los dos puntos\(\left(x_{1}, y_{1}\right)\) y\(\left(x_{2}, y_{2}\right)\) es
\(d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
- Fórmula de punto medio: El punto medio del segmento de línea cuyos extremos son los dos puntos\(\left(x_{1}, y_{1}\right)\) y\(\left(x_{2}, y_{2}\right)\) es
\(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\)
Para encontrar el punto medio de un segmento de línea, encontramos el promedio\(x\) de las coordenadas y el promedio\(y\) de las coordenadas de los puntos finales. - Círculo: Un círculo es todos los puntos en un plano que están a una distancia fija de un punto fijo en el plano. El punto dado se llama el centro,\((h,k)\), y la distancia fija se llama el radio\(r\),, del círculo.
- Forma estándar de la ecuación a círculo: La forma estándar de la ecuación de un círculo con centro\((h,k)\),, y radio\(r\), es
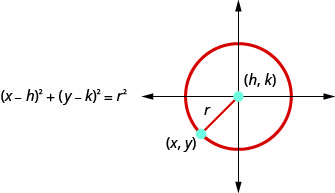
- Forma general de la ecuación de un círculo: La forma general de la ecuación de un círculo es
\(x^{2}+y^{2}+a x+b y+c=0\)
Glosario
- círculo
- Un círculo es todos los puntos en un plano que están a una distancia fija de un punto fijo en el plano.