Saltar al contenido principal
LibreTexts Español

11.6E: Ejercicios

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    112784

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    La práctica hace la perfección

    Ejercicio\(\PageIndex{17}\) Solve a System of Nonlinear Equations Using Graphing

    En los siguientes ejercicios, resuelve el sistema de ecuaciones mediante la gráfica.

    1. \(\left\{\begin{array}{l}{y=2 x+2} \\ {y=-x^{2}+2}\end{array}\right.\)
    2. \(\left\{\begin{array}{l}{y=6 x-4} \\ {y=2 x^{2}}\end{array}\right.\)
    3. \(\left\{\begin{array}{l}{x+y=2} \\ {x=y^{2}}\end{array}\right.\)
    4. \(\left\{\begin{array}{l}{x-y=-2} \\ {x=y^{2}}\end{array}\right.\)
    5. \(\left\{\begin{array}{l}{y=\frac{3}{2} x+3} \\ {y=-x^{2}+2}\end{array}\right.\)
    6. \(\left\{\begin{array}{l}{y=x-1} \\ {y=x^{2}+1}\end{array}\right.\)
    7. \(\left\{\begin{array}{l}{x=-2} \\ {x^{2}+y^{2}=4}\end{array}\right.\)
    8. \(\left\{\begin{array}{l}{y=-4} \\ {x^{2}+y^{2}=16}\end{array}\right.\)
    9. \(\left\{\begin{array}{l}{x=2} \\ {(x+2)^{2}+(y+3)^{2}=16}\end{array}\right.\)
    10. \(\left\{\begin{array}{l}{y=-1} \\ {(x-2)^{2}+(y-4)^{2}=25}\end{array}\right.\)
    11. \(\left\{\begin{array}{l}{y=-2 x+4} \\ {y=\sqrt{x}+1}\end{array}\right.\)
    12. \(\left\{\begin{array}{l}{y=-\frac{1}{2} x+2} \\ {y=\sqrt{x}-2}\end{array}\right.\)
    Responder

    2.

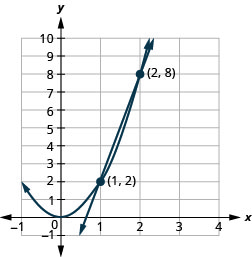
    Esta gráfica muestra las ecuaciones de un sistema, y es igual a 6 x menos 4 que es una línea e y es igual a 2 x cuadrado que es una parábola, en el plano de coordenadas x y. El vértice de la parábola es (0, 0) y la parábola se abre hacia arriba. La línea tiene una pendiente de 6. La línea y la parábola se cruzan en los puntos (1, 2) y (2, 8), los cuales están etiquetados. Las soluciones son (1, 2) y (2, 8).
    Figura 11.5.61

    4.

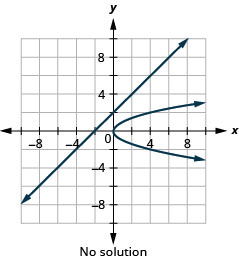
    Esta gráfica muestra las ecuaciones de un sistema, x menos y es igual a negativo 2 que es una línea y x es igual a y cuadrado que es una parábola de apertura hacia la derecha, en el plano de coordenadas x y. El vértice de la parábola es (0, 0) y pasa por los puntos (1, 1) y (1, negativo 1). La línea tiene una pendiente de 1 y una intersección en Y en 2. La línea y la parábola no se cruzan, por lo que el sistema no tiene solución.
    Figura 11.5.62

    6.

    Esta gráfica muestra las ecuaciones de un sistema, y es x menos 1 que es una línea e y es igual a x cuadrado más 1 que es una parábola de apertura hacia arriba, en el plano de coordenadas x y. El vértice de la parábola es (0, 1) y pasa por los puntos (negativo 1, 2) y (1, 2). La línea tiene una pendiente de 1 y una intersección y en negativo 1. La línea y la parábola no se cruzan, por lo que el sistema no tiene solución.
    Figura 11.5.63

    8.

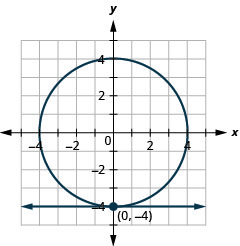
    Esta gráfica muestra las ecuaciones de un sistema, x es igual a negativo 2 que es una línea y x cuadrado más y cuadrado es igual a 16 que es un círculo, en el plano de la coordenada x y. La línea es horizontal. El centro del círculo es (0, 0) y el radio del círculo es 4. La línea y el círculo se cruzan en (negativo 2, 0), por lo que la solución del sistema es (negativo 2, 0).
    Figura 11.5.64

    10.

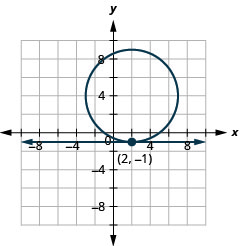
    Esta gráfica muestra las ecuaciones de un sistema, x es igual a 2 que es una línea y la cantidad x menos 2 cantidad final al cuadrado más la cantidad y menos 4 cantidad final cuadrada es igual a 25 que es un círculo, en el plano de la coordenada x y. La línea es horizontal. El centro del círculo es (2, 4) y el radio del círculo es 5. La línea y el círculo se cruzan en (2, negativo 1), por lo que la solución del sistema es (2, negativo 1).
    Figura 11.5.65

    12.

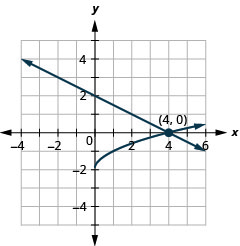
    Esta gráfica muestra las ecuaciones de un sistema, y es igual a la mitad negativa x más 2 que es una línea y la y es igual a la raíz cuadrada de x menos 2, en el plano de la coordenada x y. La curva para y es igual a la raíz cuadrada de x menos 2 La curva para y es igual a la raíz cuadrada de x más 1 donde x es mayor o igual a 0 e y es mayor o igual a negativo 2. La línea y la curva de raíz cuadrada se cruzan en (4, 0), por lo que la solución es (4, 0).
    Figura 11.5.66
    Ejercicio\(\PageIndex{18}\) Solve a System of Nonlinear Equations Using Substitution

    En los siguientes ejercicios, resolver el sistema de ecuaciones mediante la sustitución.

    1. \(\left\{\begin{array}{l}{x^{2}+4 y^{2}=4} \\ {y=\frac{1}{2} x-1}\end{array}\right.\)
    2. \(\left\{\begin{array}{l}{9 x^{2}+y^{2}=9} \\ {y=3 x+3}\end{array}\right.\)
    3. \(\left\{\begin{array}{l}{9 x^{2}+y^{2}=9} \\ {y=x+3}\end{array}\right.\)
    4. \(\left\{\begin{array}{l}{9 x^{2}+4 y^{2}=36} \\ {x=2}\end{array}\right.\)
    5. \(\left\{\begin{array}{l}{4 x^{2}+y^{2}=4} \\ {y=4}\end{array}\right.\)
    6. \(\left\{\begin{array}{l}{x^{2}+y^{2}=169} \\ {x=12}\end{array}\right.\)
    7. \(\left\{\begin{array}{l}{3 x^{2}-y=0} \\ {y=2 x-1}\end{array}\right.\)
    8. \(\left\{\begin{array}{l}{2 y^{2}-x=0} \\ {y=x+1}\end{array}\right.\)
    9. \(\left\{\begin{array}{l}{y=x^{2}+3} \\ {y=x+3}\end{array}\right.\)
    10. \(\left\{\begin{array}{l}{y=x^{2}-4} \\ {y=x-4}\end{array}\right.\)
    11. \(\left\{\begin{array}{l}{x^{2}+y^{2}=25} \\ {x-y=1}\end{array}\right.\)
    12. \(\left\{\begin{array}{l}{x^{2}+y^{2}=25} \\ {2 x+y=10}\end{array}\right.\)
    Responder

    2. \((-1,0),(0,3)\)

    4. \((2,0)\)

    6. \((12,-5),(12,5)\)

    8. Sin solución

    10. \((0,-4),(1,-3)\)

    12. \((3,4),(5,0)\)

    Ejercicio\(\PageIndex{19}\) Solve a System of Nonlinear Equations Using Elimination

    En los siguientes ejercicios, resuelve el sistema de ecuaciones mediante el uso de la eliminación.

    1. \(\left\{\begin{array}{l}{x^{2}+y^{2}=16} \\ {x^{2}-2 y=8}\end{array}\right.\)
    2. \(\left\{\begin{array}{l}{x^{2}+y^{2}=16} \\ {x^{2}-y=4}\end{array}\right.\)
    3. \(\left\{\begin{array}{l}{x^{2}+y^{2}=4} \\ {x^{2}+2 y=1}\end{array}\right.\)
    4. \(\left\{\begin{array}{l}{x^{2}+y^{2}=4} \\ {x^{2}-y=2}\end{array}\right.\)
    5. \(\left\{\begin{array}{l}{x^{2}+y^{2}=9} \\ {x^{2}-y=3}\end{array}\right.\)
    6. \(\left\{\begin{array}{l}{x^{2}+y^{2}=4} \\ {y^{2}-x=2}\end{array}\right.\)
    7. \(\left\{\begin{array}{l}{x^{2}+y^{2}=25} \\ {2 x^{2}-3 y^{2}=5}\end{array}\right.\)
    8. \(\left\{\begin{array}{l}{x^{2}+y^{2}=20} \\ {x^{2}-y^{2}=-12}\end{array}\right.\)
    9. \(\left\{\begin{array}{l}{x^{2}+y^{2}=13} \\ {x^{2}-y^{2}=5}\end{array}\right.\)
    10. \(\left\{\begin{array}{l}{x^{2}+y^{2}=16} \\ {x^{2}-y^{2}=16}\end{array}\right.\)
    11. \(\left\{\begin{array}{l}{4 x^{2}+9 y^{2}=36} \\ {2 x^{2}-9 y^{2}=18}\end{array}\right.\)
    12. \(\left\{\begin{array}{l}{x^{2}-y^{2}=3} \\ {2 x^{2}+y^{2}=6}\end{array}\right.\)
    13. \(\left\{\begin{array}{l}{4 x^{2}-y^{2}=4} \\ {4 x^{2}+y^{2}=4}\end{array}\right.\)
    14. \(\left\{\begin{array}{l}{x^{2}-y^{2}=-5} \\ {3 x^{2}+2 y^{2}=30}\end{array}\right.\)
    15. \(\left\{\begin{array}{l}{x^{2}-y^{2}=1} \\ {x^{2}-2 y=4}\end{array}\right.\)
    16. \(\left\{\begin{array}{l}{2 x^{2}+y^{2}=11} \\ {x^{2}+3 y^{2}=28}\end{array}\right.\)
    Responder

    2. \((0,-4),(-\sqrt{7}, 3),(\sqrt{7}, 3)\)

    4. \((0,-2),(-\sqrt{3}, 1),(\sqrt{3}, 1)\)

    6. \((-2,0),(1,-\sqrt{3}),(1, \sqrt{3})\)

    8. \((-2,-4),(-2,4),(2,-4),(2,4)\)

    10. \((-4,0),(4,0)\)

    12. \((-\sqrt{3}, 0),(\sqrt{3}, 0)\)

    14. \((-2,-3),(-2,3),(2,-3),(2,3)\)

    16. \((-1,-3),(-1,3),(1,-3),(1,3)\)

    Ejercicio\(\PageIndex{20}\) Use a System of Nonlinear Equations to Solve Applications

    En los siguientes ejercicios, resolver el problema utilizando un sistema de ecuaciones.

    1. La suma de dos números es\(−6\) y el producto es\(8\). Encuentra los números.
    2. La suma de dos números es\(11\) y el producto es\(−42\). Encuentra los números.
    3. La suma de los cuadrados de dos números es\(65\). La diferencia del número es\(3\). Encuentra los números.
    4. La suma de los cuadrados de dos números es\(113\). La diferencia del número es\(1\). Encuentra los números.
    5. La diferencia de los cuadrados de dos números es\(15\). La diferencia de dos veces el cuadrado del primer número y el cuadrado del segundo número es\(30\). Encuentra los números.
    6. La diferencia de los cuadrados de dos números es\(20\). La diferencia del cuadrado del primer número y dos veces el cuadrado del segundo número es\(4\). Encuentra los números.
    7. El perímetro de un rectángulo es de\(32\) pulgadas y su área es de pulgadas\(63\) cuadradas. Encuentra el largo y ancho del rectángulo.
    8. El perímetro de un rectángulo es\(52\) cm y su área es\(165\)\(\mathrm{cm}^{2}\). Encuentra el largo y ancho del rectángulo.
    9. Dion compró un nuevo microondas. La diagonal de la puerta mide\(17\) pulgadas. La puerta también tiene un área de pulgadas\(120\) cuadradas. ¿Cuál es el largo y ancho de la puerta del microondas?
    10. Jules compró un microondas para su cocina. La diagonal del frente del microondas mide\(26\) pulgadas. El frente también tiene un área de pulgadas\(240\) cuadradas. ¿Cuál es el largo y ancho del microondas?
    11. Roman encontró a la venta un televisor de pantalla ancha, pero no está seguro de si encajará en su centro de entretenimiento. El televisor es\(60\)”. El tamaño de un televisor se mide en la diagonal de la pantalla y una pantalla ancha tiene una longitud que es mayor que el ancho. La pantalla también tiene un área de pulgadas\(1728\) cuadradas. Su centro de entretenimiento tiene un inserto para el televisor con un largo de\(50\) pulgadas y ancho de\(40\) pulgadas. ¿Cuál es el largo y ancho de la pantalla del televisor y encajará en el centro de entretenimiento de Roman?
    12. Donnette encontró un televisor de pantalla ancha en una venta de garaje, pero no está seguro de si se ajustará a su centro de entretenimiento. El televisor es\(50\)”. El tamaño de un televisor se mide en la diagonal de la pantalla y una pantalla ancha tiene una longitud que es mayor que el ancho. La pantalla también tiene un área de pulgadas\(1200\) cuadradas. Su centro de entretenimiento tiene un inserto para el televisor con un largo de\(38\) pulgadas y ancho de\(27\) pulgadas. ¿Cuál es el largo y ancho de la pantalla del televisor y encajará en el centro de entretenimiento de Donnette?
    Responder

    2. \(-3\)y\(14\)

    4. \(-7\)y\(-8\) o\(8\) y\(7\)

    6. \(-6\)y\(-4\) o\(-6\) y\(4\) o\(6\) y\(-4\) o\(6\) y\(4\)

    8. Si el largo es\(11\) cm, el ancho es\(15\) cm. Si el largo es\(15\) cm, el ancho es\(11\) cm.

    10. Si el largo es\(10\) pulgadas, el ancho es\(24\) pulgadas. Si el largo es\(24\) pulgadas, el ancho es\(10\) pulgadas.

    12. El largo es\(40\) pulgadas y el ancho es\(30\) pulgadas. El televisor no encajará en el centro de entretenimiento de Donnette.

    Ejercicio\(\PageIndex{21}\) Writing Exercises
    1. En sus propias palabras, explique las ventajas y desventajas de resolver un sistema de ecuaciones mediante la gráfica.
    2. Explica con tus propias palabras cómo resolver un sistema de ecuaciones usando la sustitución.
    3. Explica con tus propias palabras cómo resolver un sistema de ecuaciones usando la eliminación.
    4. Un círculo y una parábola pueden cruzarse de maneras que resultarían en\(0, 1, 2, 3,\)\(4\) soluciones. Dibuja un boceto de cada una de las posibilidades.
    Responder

    2. Las respuestas pueden variar

    4. Las respuestas pueden variar

    Autocomprobación

    a. después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.

    Esta tabla tiene cuatro columnas y cinco filas. La primera fila es un encabezado y etiqueta a cada columna, “I can…â€, “confiadamente, ††“Con algo de ayuda, †y †œNo-I don’ t get it! †En la fila 2, el I can fue resolver un sistema de ecuaciones no lineales usando gráficos. En la fila 3, el puedo resolver un sistema de ecuaciones no lineales usando la sustitución. En la fila 4, el yo puedo fue resolver un sistema de ecuaciones no lineales usando la eliminación. En la fila 5, el I can fue usar un sistema de ecuaciones no lineales para resolver aplicaciones.
    Figura 11.5.67

    b. después de mirar la lista de verificación, ¿cree que está bien preparado para la siguiente sección? ¿Por qué o por qué no?

    This page titled 11.6E: Ejercicios is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by OpenStax via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.