3.5: Resta de números firmados
- Page ID
- 112483
Descripción general
- Definición de resta
- Resta de números firmados
Definición de resta
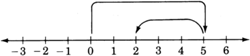
Sabemos por nuestra experiencia con la aritmética que la resta\(5−2\) produce\(3\), es decir,\(5−2=3\). Ilustrar este proceso en la recta numérica sugiere una regla para restar números firmados.

Empezamos en\(0\), el origen.
Ya que\(5\) es positivo, movemos\(5\) unidades a la derecha.
Después, movemos 2 unidades a la izquierda para llegar a\(3\). (Esto nos recuerda a la suma con un número negativo.)
Esta ilustración sugiere que\(5−2\) es lo mismo que\(5+(−2)\).
Esto nos lleva directamente a la definición de resta.
Si\(a\) y\(b\) son números reales,\(a−b\) es lo mismo que\(a+(−b)\), donde\(−b\) es lo contrario de\(b\).
Resta de números firmados
La definición anterior sugiere la regla para restar números con signo.
Para realizar la resta\(a−b\), sumar lo contrario de\(b\) a\(a\), es decir, cambiar el signo de\(b\) y sumar.
Conjunto de Muestras A
Realizar las restaciones.
\(5−3=5+(−3)=2\)
\(4−9=4+(−9)=−5\)

\(−4−6=−4+(−6)=−10\)

\(−3−(−12)=−3+12=9\)

\(0−(−15)=0+15=15\)

La alta temperatura hoy en Lake Tahoe era de 26F. Se espera que la baja temperatura de esta noche sea −7F. ¿Cuántos grados se espera que baje la temperatura?
Necesitamos encontrar la diferencia entre 26 y −7.
\(26−(−7)=26+7=33\)
Por lo tanto, la caída de temperatura esperada es de 33F.
\ (\ begin {alineado}
-6- (-5) -10 &=-6+5+ (-10)\\
& =( -6+5) + (-10)\\
&=-1+ (-10)\\
&=-11
\ end {alineado}\)
Conjunto de práctica A
Realizar las restaciones.
\(9−6\)
- Responder
-
\(3\)
\(6-9\)
- Responder
-
\(-3\)
\(0-7\)
- Responder
-
\(-7\)
\(1-14\)
- Responder
-
\(-13\)
\(-8-12\)
- Responder
-
\(-20\)
\(-21-6\)
- Responder
-
\(-27\)
\(-6-(-4)\)
- Responder
-
\(-2\)
\(8-(-10)\)
- Responder
-
\(18\)
\(1-(-12)\)
- Responder
-
\(13\)
\(86-(-32)\)
- Responder
-
\(118\)
\(0-16\)
- Responder
-
\(-16\)
\(0-(-16)\)
- Responder
-
\(16\)
\(0-(8)\)
- Responder
-
\(-8\)
\(5-(-5)\)
- Responder
-
\(10\)
\(24-(-(-24))\)
- Responder
-
\(0\)
Ejercicios
Para los siguientes ejercicios, realice las operaciones indicadas.
\(8-3\)
- Responder
-
\(5\)
\(12 - 7\)
- Responder
-
\(5\)
\(5-6\)
- Responder
-
\(-1\)
\(14 - 30\)
\(2 - 15\)
- Responder
-
\(-13\)
\(5 - 18\)
- Responder
-
\(-13\)
\(1 - 7\)
- Responder
-
\(-6\)
\(4 - 11\)
\(-6 - 5\)
- Responder
-
\(-11\)
\(-8 - 14\)
\(-1 - 12\)
- Responder
-
\(-13\)
\(-4 - 4\)
\(-6 - 8\)
- Responder
-
\(-14\)
\(-1 - 12\)
- Responder
-
\(-13\)
\(-5 - (-3)\)
- Responder
-
\(-2\)
\(-11 - (-8)\)
\(-7 -(-12)\)
- Responder
-
\(5\)
\(-2 -(-10)\)
\(-4 -(-15)\)
- Responder
-
\(11\)
\(-11 -(-16)\)
\(-1 -(-6)\)
- Responder
-
\(5\)
\(-8 -(-14)\)
\(-15 -(-10)\)
- Responder
-
\(-5\)
\(-11 -(-4)\)
\(-16 -(-8)\)
- Responder
-
\(-8\)
\(-12 -(-11)\)
\(0 - 6\)
- Responder
-
\(-6\)
\(0 - 15\)
\(0 - (-7)\)
- Responder
-
\(7\)
\(0 - (-10)\)
\(67 - 38\)
- Responder
-
\(29\)
\(142 - 85\)
\(816 - 1140\)
- Responder
-
\(-324\)
\(105-421\)
\(-550 - (-121)\)
- Responder
-
\(-429\)
\(−15.016−(4.001)\)
\(−26+7−52\)
- Responder
-
\(-71\)
\(−15−21−(−2)\)
\(−104−(−216)−(−52)\)
- Responder
-
\(164\)
\(−0.012−(−0.111)−(0.035)\)
\([5+(−6)]−[2+(−4)]\)
- Responder
-
\(1\)
\([2+(−8)]−[5+(−7)]\)
\([4+(−11)]−[2+(−10)]\)
- Responder
-
\(1\)
\([9+(−6)]−[4+(−12)]\)
\((11−8)−(1−6)\)
- Responder
-
\(8\)
\((5−12)−(4−10)\)
\((1−10)−(2−15)\)
- Responder
-
\(4\)
\((0−8)−(4−12)\)
\((−4+7)−(2−5)\)
- Responder
-
\(6\)
\((−6+2)−(5−11)\)
\([−8+(−5+3)]−[9−(−3−5)]\)
- Responder
-
\(-27\)
\([−4+(−1+6)]−[7−(−6−1)]\)
\([2−(−6+10)]−[1−(2−11)]\)
- Responder
-
\(-12\)
\([5−(−2−5)]−[2−(−1−4)]\)
Cuando una máquina en particular está funcionando correctamente, su medidor leerá 34. Si un rodamiento roto en la máquina hace que la lectura del medidor baje 45 unidades, ¿cuál es la lectura del medidor?
- Responder
-
\(-11\)
La baja temperatura hoy en Denver fue de −4F y la alta fue de 42F. ¿Cuál es la diferencia de temperatura?
Ejercicios para revisión
Utilice la propiedad distributiva para expandir\(4x(5y+11)\)
- Responder
-
\(20xy + 44x\)
Simplificar\(\dfrac{2(3x^2y^2)^3(2x^4y^3)^0}{27x^4y^3}\). Supongamos\(x \not = 0\),\(y \not = 0\)
Simplificar\(|-(4^2+2^2-3^2)|\).
- Responder
-
\(11\)
Encuentra la suma. \(-8 + (-14)\)
Encuentra la suma. \(3 + (-6)\).
- Responder
-
\(-3\)


