7.2: Graficar ecuaciones lineales y desigualdades en una variable

Última actualización
Guardar como PDF

Page ID: 112321

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Gráficas

Hasta el momento en nuestro estudio del álgebra, hemos desarrollado y utilizado varios métodos para obtener soluciones a ecuaciones lineales tanto en una como en dos variables. Muy a menudo es útil obtener una imagen de las soluciones a una ecuación. Estas imágenes se llaman gráficas y pueden revelar información que puede no ser evidente solo a partir de la ecuación.

La Gráfica de una Ecuación

La representación geométrica (imagen) de las soluciones a una ecuación se llama la gráfica de la ecuación.

Ejes, sistemas de coordenadas y cotas

Axis

La estructura básica de la gráfica es el eje. Es con respecto al eje donde se localizan todas las soluciones a una ecuación. El tipo de eje más fundamental es la recta numérica.

La línea numérica es un eje

$Una línea numérica con flechas en cada extremo y está etiquetada de cinco negativos a cinco en incrementos de uno. Hay una flecha apuntando hacia la recta numérica con la etiqueta, 'Esta recta numérica es un eje'.$

Tenemos las siguientes reglas generales respecto a los ejes.

Número de variables y número de ejes

Una ecuación en una variable requiere un eje.
Una ecuación en dos variables requiere dos ejes.
Una ecuación en tres variables requiere tres ejes.
... Una ecuación en nn variables requiere nn ejes.

Siempre dibujaremos un eje como línea recta, y si se requiere más de un eje, los dibujaremos para que todos sean mutuamente perpendiculares (las líneas que forman los ejes estarán en ángulos de 90° entre sí).

Sistema de coordenadas

Un sistema de ejes construidos para graficar una ecuación se llama sistema de coordenadas.

La Frase, Graficando una Ecuación La frase que grafica una ecuación se usa con frecuencia y debe interpretarse como que significa ubicar geométricamente las soluciones a una ecuación.

Relacionar el número de variables y el número de ejes

No empezaremos realmente a graficar ecuaciones hasta la Sección 7.3, pero en los siguientes ejemplos, relacionaremos el número de variables en una ecuación con el número de ejes en el sistema de coordenadas.

1. Gráficas unidimensionales:

Si queremos graficar la ecuación$5x+2=17$, necesitaríamos construir un sistema de coordenadas que consista en un solo eje (una sola línea numérica) ya que la ecuación consiste en una sola variable. Etiquetamos el eje con la variable que aparece en la ecuación.

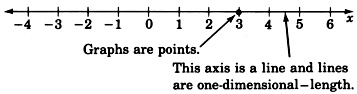
$Una línea numérica con flechas en cada lado etiquetadas de cuatro negativos a seis en incrementos de uno. La línea numérica está etiquetada x. Hay una flecha que apunta hacia la recta numérica con la etiqueta, 'Este eje es una línea y las líneas son de longitud unidimensional. ' Hay otra flecha apuntando hacia el número tres con una etiqueta, 'Las gráficas son puntos'.$

Podríamos interpretar una ecuación en una variable como dar información en un espacio unidimensional. Dado que vivimos en el espacio tridimensional, el espacio unidimensional puede ser difícil de imaginar. Los objetos en el espacio unidimensional solo tendrían longitud, sin ancho ni profundidad.

2. Gráficas bidimensionales:

Para graficar una ecuación en dos variables como$y=2x–3y$, necesitaríamos construir un sistema de coordenadas consistente en dos líneas numéricas mutuamente perpendiculares (ejes). Llamamos origen a la intersección de los dos ejes y la etiquetamos con un 0. Los dos ejes son simplemente líneas numéricas; uno dibujado horizontalmente, otro dibujado verticalmente.

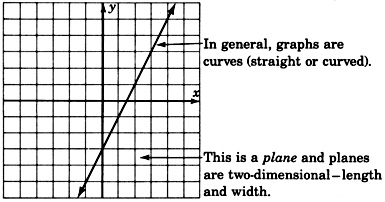
$Un plano xy con líneas de cuadrícula y una línea recta que pasa por los cuadrantes uno, tres y cuatro. Hay una flecha apuntando hacia esta línea con la etiqueta 'En general, las gráficas son curvas (rectas o curvas) '. Hay otra flecha apuntando hacia el plano xy con la etiqueta 'Este es un plano y los planos son bidimensionales: largo y ancho'.$

Recordemos que una ecuación en dos variables requiere de una solución para ser un par de números. Las soluciones se pueden escribir como pares ordenados$(x,y)$. Ya que la ecuación$y=2x–3$ involucra las variables$x$ y$y$, etiquetamos un eje$x$ y el otro eje$y$. En matemáticas, se acostumbra etiquetar el eje horizontal con la variable independiente y el eje vertical con la variable dependiente.

Podríamos interpretar ecuaciones en dos variables como dar información en el espacio bidimensional. Los objetos en el espacio bidimensional tendrían longitud y anchura, pero no profundidad.

3. Gráficas tridimensionales:

Una ecuación en tres variables, tales como$3x^2–4y^2+5z=0$, requiere tres ejes mutuamente perpendiculares, uno para cada variable. Construiríamos el siguiente sistema de coordenadas y gráfica.

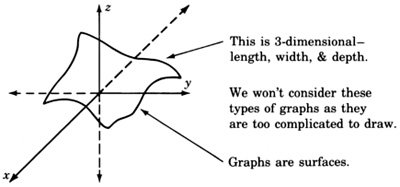
$Un plano tridimensional x y z y una gráfica de una superficie arbitraria. Hay flechas apuntando hacia la superficie con las siguientes etiquetas: 'Esto es tridimensional: largo, ancho y profundidad. Las gráficas son superficies. No vamos a considerar este tipo de gráficas ya que son demasiado complicadas de dibujar. '$

Podríamos interpretar ecuaciones en tres variables como información sobre el espacio tridimensional.

4. Gráficas cuatridimensionales

Para graficar una ecuación en cuatro variables, tales como$3x–2y+8x–5w=–7$, requeriría cuatro líneas numéricas mutuamente perpendiculares. Estas gráficas se dejan a la imaginación.

Podríamos interpretar ecuaciones en cuatro variables como dar información en el espacio de cuatro dimensiones. Los objetos de cuatro dimensiones tendrían longitud, anchura, profundidad y alguna otra dimensión.

Agujeros Negros

Estos otros espacios son difíciles de imaginar para nosotros, pero la existencia de “agujeros negros” hace que la posibilidad de otros universos de una, dos, cuatro o n dimensiones no sea del todo improbable. Aunque puede ser difícil para nosotros personas “3-D” viajar en otro espacio dimensional, ¡al menos podríamos estar bastante seguros de que nuestras matemáticas seguirían funcionando (ya que no se restringe a solo tres dimensiones)!

Graficar en una dimensión

Graficar una ecuación lineal en una variable implica resolver la ecuación, luego ubicar la solución en el eje (línea numérica) y marcar un punto en esta ubicación. Hemos observado que las gráficas pueden revelar información que puede no ser evidente a partir de la ecuación original. Las gráficas de ecuaciones lineales en una variable no arrojan mucha, si la hay, información, sino que sirven como base para gráficas de mayor dimensión (gráficas de dos variables y tres variables).

Conjunto de Muestras A

Ejemplo$\PageIndex{1}$

Grafica la ecuación$3x–5=10$.

Resolver la ecuación$x$ y construir un eje. Como solo hay una variable, necesitamos un solo eje. Etiquete el eje$x$.

\ (\ begin {alineado}
3x-5&=&10\\
3x&=&15\
x&=&5
\ end {alineado}\)

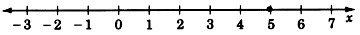
$Una línea numérica etiquetada con x con flechas en cada extremo, etiquetada de tres a siete negativos, en incrementos de uno. Hay un círculo cerrado en cinco.$

Ejemplo$\PageIndex{2}$

Grafica la ecuación$3x + 4 + 7x - 1 + 8 = 31$.

Resolviendo la ecuación que obtenemos,

\ (\ begin {alineado}
10x+11&=&31\\
10x&+&20\
x&=&2
\ end {alineado}\)

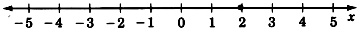
$Una línea numérica etiquetada con x con flechas en cada extremo, etiquetada de cinco a cinco negativos, en incrementos de uno. Hay un círculo cerrado en dos.$

Conjunto de práctica A

Problema de práctica$\PageIndex{1}$

Graficar la ecuación$4x + 1 = -7$

$Una línea horizontal con flechas en ambos extremos.$

Contestar

$x = -2$

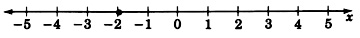
$Una línea numérica etiquetada con x con flechas en cada extremo, etiquetada de cinco a cinco negativos, en incrementos de uno. Hay un círculo cerrado en negativo dos.$

Conjunto de Muestras B

Ejemplo$\PageIndex{3}$

Grafica la desigualdad lineal$4x /ge 12$.

Se procede resolviendo la desigualdad.

\ (\ begin {alineado}
4x&\ ge&12&\ text {Divide cada lado por} 4\\
x&\ ge&3
\ end {alineado}\)

Como sabemos, cualquier valor mayor o igual a 3 satisfará la desigualdad original. De ahí que tengamos infinitamente muchas soluciones y, así, infinitamente muchos puntos para marcar en nuestra gráfica.

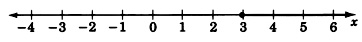
$Una línea numérica etiquetada con x con flechas en cada extremo, etiquetada de cuatro a seis negativos, en incrementos de uno. Hay un círculo cerrado en tres con una flecha sombreada oscura a la derecha de tres.$

El círculo cerrado a 3 significa que 3 se incluye como solución. Todos los puntos que comienzan en 3 y en la dirección de la flecha son soluciones.

Ejemplo$\PageIndex{4}$

Grafica la desigualdad lineal$-2y-1 > 3$.

Primero resolvemos la desigualdad.

\ (\ begin {aligned}
-2y-1& > &3\\
-2y& > &4\\
y& < &-2&\ text {El símbolo de desigualdad invertió dirección porque dividimos por} -2
\ end {alineado}\)

Así, todos los números estrictamente menores que$-2$ satisfarán la desigualdad y, por lo tanto, son soluciones.

Dado que$-2$ en sí mismo no se debe incluir como solución, dibujamos un círculo abierto en$−2$. Las soluciones están a la izquierda de$−2$ por lo que dibujamos una flecha apuntando a la izquierda de$−2$ para denotar la región de soluciones.

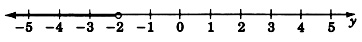
$Una línea numérica etiquetada y con flechas en cada extremo, etiquetada de cinco a cinco negativos, en incrementos de uno. Hay un círculo abierto sobre el negativo dos con una flecha oscura sombreada a la izquierda del negativo dos.$

Ejemplo$\PageIndex{5}$

Grafica la desigualdad$-2 \le y+1 < 1$.

Reconocemos esta desigualdad como una desigualdad compuesta y la resolvemos restando 1 de las tres partes.

\ (\ begin {alineado}
-2\ le y+1 < 1\\
-3\ le y < 0
\ end {alineado}\)

Así, la solución son todos los números entre −3 y 0, más precisamente, todos los números mayores o iguales a −3 pero estrictamente menores que 0.

$Una línea numérica etiquetada y con flechas en cada extremo, y etiquetada de cinco a cinco negativos en incrementos de uno. Hay un círculo cerrado en negativo tres y un círculo abierto en cero, con una línea sombreada negra que conecta los dos círculos.$

Ejemplo$\PageIndex{6}$

Grafica la ecuación lineal$5x = -125$.

La solución es$x = -25$. Escalando el eje por unidades de$5$ más que$1$, obtenemos

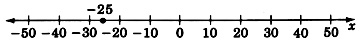
$Una línea numérica etiquetada x con flechas en cada extremo, y etiquetada de cincuenta a cincuenta negativos en incrementos de diez. Hay un círculo cerrado etiquetado como negativo veinticinco, a medio camino entre treinta negativos y veinte negativos.$

Set de práctica B

Problema de práctica$\PageIndex{2}$

Graficar la desigualdad$3x \le 18$

$Una línea horizontal con flechas en ambos extremos.$

Contestar

$x \le 6$

$Una línea numérica etiquetada con x con flechas en cada extremo, etiquetada de negativo dos a ocho, en incrementos de uno. Hay un círculo cerrado en seis con una flecha oscura sombreada a la izquierda de seis.$

Problema de práctica$\PageIndex{3}$

Grafica la desigualdad$−3m+1<13$.

$Una línea horizontal con flechas en ambos extremos.$

Contestar

$m>−4$

$Una línea numérica etiquetada con m con flechas en cada extremo, etiquetada de cinco a cinco negativos, en incrementos de uno. Hay un círculo abierto sobre el cuatro negativo con una flecha sombreada oscura a la derecha del cuatro negativo.$

Problema de práctica$\PageIndex{4}$

Grafica la desigualdad$−3≤x−5<5$.

$Una línea horizontal con flechas en ambos extremos.$

Contestar

$2≤x<10$

$Una línea numérica etiquetada x con flechas en cada extremo, y etiquetada de uno a once en incrementos de uno. Hay un círculo cerrado a las dos y un círculo abierto a las diez, con una línea sombreada negra que conecta los dos círculos.$

Problema de práctica$\PageIndex{5}$

Grafica la ecuación lineal$−6y=480$.

$Una línea horizontal con flechas en ambos extremos.$

Contestar

$y=−80$

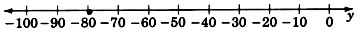
$Una línea numérica etiquetada y con flechas en cada extremo, etiquetada de cien negativo a cero, en incrementos de diez. Hay un círculo cerrado en negativo ochenta.$

Ejercicios

Para los problemas 1 - 25, graficar las ecuaciones lineales y las desigualdades.

Ejercicio$\PageIndex{1}$

$4x+7=19$

$Una línea horizontal con flechas en ambos extremos.$

Contestar

$x=3$

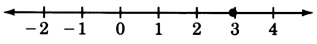
$Una línea numérica con flechas en cada extremo, etiquetada de dos negativos a cuatro en incrementos de uno. Hay un círculo cerrado a las tres.$

Ejercicio$\PageIndex{2}$

$8x−1=7$

$Una línea horizontal con flechas en ambos extremos.$

Ejercicio$\PageIndex{3}$

$2x+3=4$

$Una línea horizontal con flechas en ambos extremos.$

Contestar

$x = \dfrac{1}{2}$

$Una línea numérica con flechas en cada extremo, etiquetada de dos negativos a cuatro en incrementos de uno. Hay un círculo cerrado en un punto entre cero y uno.$

Ejercicio$\PageIndex{4}$

$x+3=15$

$Una línea horizontal con flechas en ambos extremos.$

Ejercicio$\PageIndex{5}$

$6y+3=y+8$

$Una línea horizontal con flechas en ambos extremos.$

Contestar

$y=1$

$Una línea numérica con flechas en cada extremo, etiquetada de dos negativos a cuatro en incrementos de uno. Hay un círculo cerrado a la una.$

Ejercicio$\PageIndex{6}$

$2x=0$

$Una línea horizontal con flechas en ambos extremos.$

Ejercicio$\PageIndex{7}$

$4+1−4=3z$

$Una línea horizontal con flechas en ambos extremos.$

Contestar

$z = \dfrac{1}{3}$

$Una línea numérica con flechas en cada extremo, etiquetada de uno a dos negativos en incrementos de un tercio. Hay un círculo cerrado a un tercio.$

Ejercicio$\PageIndex{8}$

$x + \dfrac{1}{2} = \dfrac{4}{3}$

$Una línea horizontal con flechas en ambos extremos.$

Ejercicio$\PageIndex{9}$

$7r = \dfrac{1}{4}$

$Una línea horizontal con flechas en ambos extremos.$

Responder

$r = \dfrac{1}{28}$

$Una línea numérica con flechas en cada extremo, etiquetada de uno negativo sobre veintiocho a tres sobre veintiocho en incrementos de un veintiocho. Hay un círculo cerrado en negativo uno sobre veintiocho.$

Ejercicio$\PageIndex{10}$

$2x - 6 = \dfrac{2}{5}$

$Una línea horizontal con flechas en ambos extremos.$

Ejercicio$\PageIndex{11}$

$x+7≤12$

$Una línea horizontal con flechas en ambos extremos.$

Responder

$x≤5$

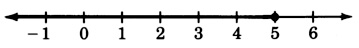
$Una línea numérica con flechas en cada extremo, etiquetada de negativo uno a seis, en incrementos de uno. Hay un círculo cerrado a las cinco. De este círculo se origina una flecha oscura, y que se dirige hacia la izquierda de cinco.$

Ejercicio$\PageIndex{12}$

$y−5<3$

$Una línea horizontal con flechas en ambos extremos.$

Ejercicio$\PageIndex{13}$

$x+19>2$

$Una línea horizontal con flechas en ambos extremos.$

Responder

$x>−17$

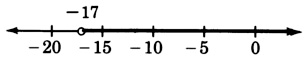
$Una línea numérica con flechas en cada extremo, etiquetada de veinte negativo a cero, en incrementos de cinco. Hay un círculo abierto a los diecisiete negativos. Una flecha oscura se origina de este círculo, y rumbo hacia la derecha de diecisiete negativos.$

Ejercicio$\PageIndex{14}$

$z+5>11$

$Una línea horizontal con flechas en ambos extremos.$

Ejercicio$\PageIndex{15}$

$3m−7≤8$

$Una línea horizontal con flechas en ambos extremos.$

Responder

$m≤5$

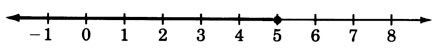
$Una línea numérica con flechas en cada extremo, etiquetada de negativo uno a ocho, en incrementos de uno. Hay un círculo cerrado a las cinco. De este círculo se origina una flecha oscura, y que se dirige hacia la izquierda de cinco.$

Ejercicio$\PageIndex{16}$

$−5t≥10$

$Una línea horizontal con flechas en ambos extremos.$

Ejercicio$\PageIndex{17}$

$−8x−6≥34$

$Una línea horizontal con flechas en ambos extremos.$

Responder

$x≤−5$

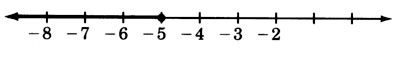
$Una línea numérica con flechas en cada extremo, etiquetada de ocho negativo a negativo dos, en incrementos de uno. Hay un círculo cerrado en negativo cinco. Una flecha oscura se origina en este círculo, y que se dirige hacia la izquierda de cinco negativos.$

Ejercicio$\PageIndex{18}$

$\dfrac{x}{4} < 2$

$Una línea horizontal con flechas en ambos extremos.$

Ejercicio$\PageIndex{19}$

$\dfrac{y}{7} \le 3$

$Una línea horizontal con flechas en ambos extremos.$

Responder

$y≤21$

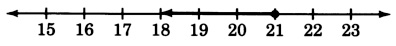
$Una línea numérica con flechas en cada extremo, etiquetada de quince a veintitrés, en incrementos de uno. Hay un círculo cerrado a los veintiún años. De este círculo se origina una flecha oscura, y se dirige hacia la izquierda de veintiún.$

Ejercicio$\PageIndex{20}$

$\dfrac{2y}{9} \ge 4$

$Una línea horizontal con flechas en ambos extremos.$

Ejercicio$\PageIndex{21}$

$\dfrac{-5y}{8} \le 4$

$Una línea horizontal con flechas en ambos extremos.$

Responder

$y \ge -\dfrac{32}{5}$

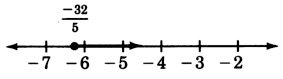
$Una línea numérica con flechas en cada extremo, etiquetada de siete negativos a dos negativos, en incrementos de uno. Hay un círculo cerrado en un punto entre seis negativos y siete negativos etiquetados como negativos treinta y dos sobre cinco. Una flecha oscura se origina de este círculo, y rumbo hacia la derecha de treinta y dos negativos.$

Ejercicio$\PageIndex{22}$

$\dfrac{-6a}{7} < -4$

$Una línea horizontal con flechas en ambos extremos.$

Ejercicio$\PageIndex{23}$

$−1≤x−3<0$

$Una línea horizontal con flechas en ambos extremos.$

Responder

$2≤x<3$

$Una línea numérica con flechas en cada extremo, etiquetada de cero a cuatro en incrementos de uno. Hay un círculo cerrado a las dos, y un círculo abierto a las tres. Estos círculos están conectados por una línea negra.$

Ejercicio$\PageIndex{24}$

$6≤x+4≤7$

$Una línea horizontal con flechas en ambos extremos.$

Ejercicio$\PageIndex{25}$

$−12<−2x−2≤−8$

$Una línea horizontal con flechas en ambos extremos.$

Responder

$3≤x<5$

$Una línea numérica con flechas en cada extremo, etiquetada de dos a cinco en incrementos de uno. Hay un círculo cerrado a las tres y un círculo abierto a las cinco. Estos círculos están conectados por una línea negra.$

Ejercicios para revisión

Ejercicio$\PageIndex{26}$

Simplificar$(3x^8y^2)^3$.

Ejercicio$\PageIndex{27}$

Enumerar, en su caso, los factores comunes en la expresión$10x^4−15x^2+5x^6$.

Responder: $5x^2$

Ejercicio$\PageIndex{28}$

Resolver la desigualdad$−4(x+3)<−3x+1$.

Ejercicio$\PageIndex{29}$

Resuelve la ecuación$y=−5x+8$ si$x=−2$.

Responder: $(−2,18)$

Ejercicio$\PageIndex{30}$

Resuelve la ecuación$2y=5(3x+7)$ si$x=−1$.

Gráficas

La Gráfica de una Ecuación

Ejes, sistemas de coordenadas y cotas

Sistema de coordenadas

Graficar en una dimensión

Conjunto de Muestras A

Ejemplo\(\PageIndex{1}\)

Ejemplo\(\PageIndex{2}\)

Conjunto de práctica A

Problema de práctica\(\PageIndex{1}\)

Conjunto de Muestras B

Ejemplo\(\PageIndex{3}\)

Ejemplo\(\PageIndex{4}\)

Ejemplo\(\PageIndex{5}\)

Ejemplo\(\PageIndex{6}\)

Set de práctica B

Problema de práctica\(\PageIndex{2}\)

Problema de práctica\(\PageIndex{3}\)

Problema de práctica\(\PageIndex{4}\)

Problema de práctica\(\PageIndex{5}\)

Ejercicios

Ejercicio\(\PageIndex{1}\)

Ejercicio\(\PageIndex{2}\)

Ejercicio\(\PageIndex{3}\)

Ejercicio\(\PageIndex{4}\)

Ejercicio\(\PageIndex{5}\)

Ejercicio\(\PageIndex{6}\)

Ejercicio\(\PageIndex{7}\)

Ejercicio\(\PageIndex{8}\)

Ejercicio\(\PageIndex{9}\)

Ejercicio\(\PageIndex{10}\)

Ejercicio\(\PageIndex{11}\)

Ejercicio\(\PageIndex{12}\)

Ejercicio\(\PageIndex{13}\)

Ejercicio\(\PageIndex{14}\)

Ejercicio\(\PageIndex{15}\)

Ejercicio\(\PageIndex{16}\)

Ejercicio\(\PageIndex{17}\)

Ejercicio\(\PageIndex{18}\)

Ejercicio\(\PageIndex{19}\)

Ejercicio\(\PageIndex{20}\)

Ejercicio\(\PageIndex{21}\)

Ejercicio\(\PageIndex{22}\)

Ejercicio\(\PageIndex{23}\)

Ejercicio\(\PageIndex{24}\)

Ejercicio\(\PageIndex{25}\)

Ejercicios para revisión

Ejercicio\(\PageIndex{26}\)

Ejercicio\(\PageIndex{27}\)

Ejercicio\(\PageIndex{28}\)

Ejercicio\(\PageIndex{29}\)

Ejercicio\(\PageIndex{30}\)