7.3: Trazando puntos en el plano

Última actualización
Guardar como PDF

Page ID: 112300

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

El avión

Pares Pedidos

Ahora nos interesa estudiar gráficas de ecuaciones lineales en dos variables. Sabemos que las soluciones a ecuaciones en dos variables consisten en un par de valores, un valor por cada variable. Hemos llamado a estos pares de valores pares ordenados. Ya que tenemos un par de valores para graficar, debemos tener un par de ejes (líneas numéricas) sobre los que se puedan ubicar los valores.

Origen

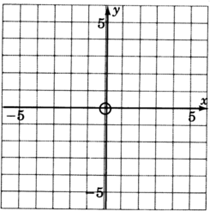
Dibujamos los ejes para que sean perpendiculares entre sí y para que se crucen entre sí en sus 0's, a este punto se le llama origen.

$Un plano de coordenadas xy con líneas de cuadrícula, etiquetado como cinco negativos y cinco con incrementos de uno en ambos ejes.$

Sistema de coordenadas rectangulares

Estas dos líneas forman lo que se llama un sistema de coordenadas rectangulares. También determinan un avión.

$xy$-avión

Un plano es una superficie plana, y un resultado de la geometría establece que a través de dos líneas de intersección cualesquiera (los ejes) se puede pasar exactamente un plano (superficie plana). Si estamos tratando con una ecuación lineal en las dos variables$x$ y$y$, a veces decimos que estamos graficando la ecuación usando un sistema de coordenadas rectangulares, o que estamos graficando la ecuación en el$xy$ plano.

Cuadrante

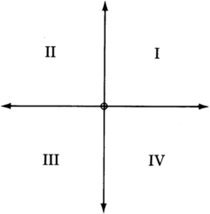
Observe que los dos ejes de coordenadas que se cruzan dividen el plano en cuatro regiones iguales. Dado que hay cuatro regiones, llamamos a cada una un cuadrante y las numeramos en sentido contrario a las agujas del reloj usando números romanos.

$Un sistema de coordenadas rectangulares con cuadrantes etiquetados como I, II, III y IV comenzando en el cuadrante ubicado en la parte superior derecha y dando vueltas en sentido antihorario.$

Recordemos que cuando estudiamos por primera vez la recta numéricaobservamos lo siguiente:

Para cada número real existe un punto único en la recta numérica, y para cada punto de la recta numérica podemos asociar un número real único.

Tenemos una situación similar para el avión.

Para cada par ordenado$(a, b)$, existe un punto único en el plano, y a cada punto del plano podemos asociar un par ordenado único$(a, b)$ de números reales.

Coordenadas de un punto

Coordenadas de un punto

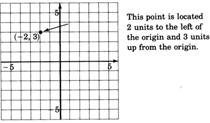
Los números en un par ordenado que están asociados a un punto en particular se denominan las coordenadas del punto. El primer número del par ordenado expresa la distancia horizontal del punto y la dirección (izquierda o derecha) desde el origen. El segundo número expresa la distancia vertical del punto y la dirección (arriba o abajo) desde el origen.

Las coordenadas determinan la distancia y la dirección

Un número positivo significa una dirección hacia la derecha o hacia arriba. Un número negativo significa una dirección hacia la izquierda o hacia abajo.

$Un punto con coordenadas negativas dos, tres trazadas en sistema de coordenadas rectangulares con el mensaje de texto 'Este punto se ubica dos unidades a la izquierda del origen y tres unidades hacia arriba del origen'. escrito en la zona exterior del plano.$

Puntos de trazado

Dado que los puntos y los pares ordenados están tan estrechamente relacionados, los dos términos a veces se usan indistintamente. Las siguientes dos frases tienen el mismo significado:

Trazar el punto$(a, b)$.
Trazar el par ordenado$(a, b)$.

Trazado de un punto

Ambas frases significan: Localizar, en el plano, el punto asociado al par ordenado$(a, b)$ y dibujar una marca en esa posición.

Conjunto de Muestras A

Ejemplo$\PageIndex{1}$

Trazar el par ordenado$(2, 6)$.

Comenzamos en el origen. El primer número del par ordenado, 2, nos dice que movemos 2 unidades a la derecha ($+2$significa 2 unidades a la derecha) El segundo número en el par ordenado, 6, nos dice que movemos 6 unidades hacia arriba ($+6$significa 6 unidades hacia arriba).

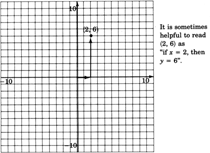
$Un plano de coordenadas xy de diez negativos a diez con incrementos de uno. La gráfica contiene una flecha desde el origen hasta un punto dos unidades a la derecha del origen y otra flecha desde el final de la primera flecha hasta un punto seis unidades arriba. La coordenada del punto donde termina la segunda flecha son dos, seis. Hay un mensaje de texto con la gráfica que dice: 'A veces es útil leer dos, seis' como 'si x es igual a dos, entonces y igual a seis'.$

A veces es útil leer$(2,6)$ como “si$x = 2$, entonces$y = 6$.

Conjunto de práctica A

Problema de práctica$\PageIndex{1}$

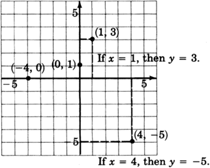
Trazar los pares ordenados.

$(1, 3), (4, −5), (0, 1), (−4, 0)$.

$Un plano de coordenadas xy con líneas de cuadrícula, etiquetado como cinco negativos y cinco con incrementos de uno en ambos ejes.$

Contestar

(Observe que las líneas punteadas en la gráfica son solo para ilustración y no deben incluirse al trazar puntos).

$Un plano de coordenadas xy con líneas de cuadrícula, etiquetado como cinco negativos y cinco con incrementos de uno en ambos ejes. La gráfica contiene cuatro pares de coordenadas trazadas: cuatro negativos, cero; uno, tres; cero, uno; y cuatro, cinco negativos.$

Ejercicios

Ejercicio$\PageIndex{1}$

Trazar los siguientes pares ordenados. (No dibujar las flechas como en el Conjunto de Práctica A.)
$(8, 2), (10, −3), (−3, 10), (0, 5), (5, 0), (0, 0), (−7, -\dfrac{3}{2})$.

$Un plano de coordenadas xy con líneas de cuadrícula, etiquetado negativo diez y diez con incrementos de uno en ambos ejes.$

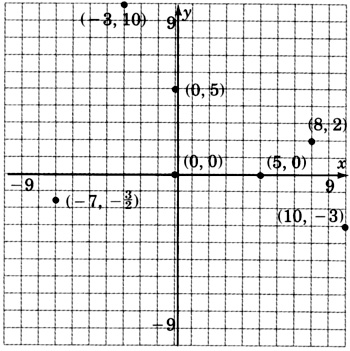
Contestar: $Total de siete puntos trazados en un plano de coordenadas xy. Las coordenadas de estos puntos son negativas tres, diez; cero, cinco; cero, cero; cinco, cero; ocho, dos; diez, negativo tres; y negativo siete, negativo tres sobre dos.$

Ejercicio$\PageIndex{2}$

Con la mayor precisión posible, indique las coordenadas de los puntos que se hayan trazado en la siguiente gráfica.

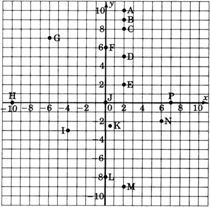
$Un plano de coordenadas xy con líneas de cuadrícula, etiquetado negativo diez y diez con incrementos de uno en ambos ejes y etiquetas cada dos unidades. Se trazan los puntos A, B, C, D, E, F, G, H, I, J, K, L, M, N, P sin especificar las coordenadas de cada punto.$

Ejercicio$\PageIndex{3}$

Usando notación de pares ordenados, ¿cuáles son las coordenadas del origen?

Contestar: Las coordenadas del origen son$(0,0)$.

Ejercicio$\PageIndex{4}$

Sabemos que las soluciones a ecuaciones lineales en dos variables se pueden expresar como pares ordenados. De ahí que las soluciones se puedan representar como puntos en el plano. Considera la ecuación lineal$y=2x−1$. Encuentre al menos diez soluciones a esta ecuación eligiendo$x$ -valores entre$−4$ y$5$ y calculando los valores y correspondientes. Trazar estas soluciones en el sistema de coordenadas a continuación. Rellena la tabla para ayudarte a realizar un seguimiento de los pares ordenados.

$x$

$y$

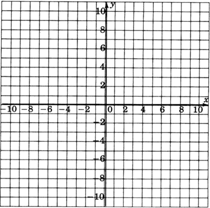
$Un plano de coordenadas xy con líneas de cuadrícula, de diez a diez negativos en incrementos de uno en ambos ejes y etiquetas cada dos unidades.$

Teniendo en cuenta que hay infinitamente muchas soluciones de pares ordenados para$y=2x−1$, especular sobre la estructura geométrica de la gráfica de todas las soluciones. Complete la siguiente declaración:

El nombre del tipo de estructura geométrica de la gráfica de todas las soluciones a la ecuación lineal
$y=2x−1$ parece ser __________.

¿Dónde cruza esta figura el eje y? ¿Este número aparece en la ecuación$y=2x−1$?

Coloca tu lápiz en cualquier punto de la figura (es posible que tengas que conectar los puntos para ver la figura con claridad). Mueve tu lápiz exactamente una unidad hacia la derecha (horizontalmente). Para volver a la figura, debes mover tu lápiz ya sea hacia arriba o hacia abajo un número determinado de unidades. ¿Cuántas unidades debes moverte verticalmente para volver a la figura, y ves este número en la ecuación$y=2x−1$?

Ejercicio$\PageIndex{5}$

Considera el$xy$ -avión.

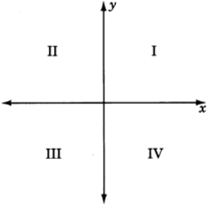
$Un sistema de coordenadas rectangulares con cuadrantes etiquetados I, II, III y IV comenzando en el cuadrante ubicado en la parte superior derecha y dando vueltas en sentido antihorario.$

Completar la tabla escribiendo las desigualdades apropiadas.

I	II	III	IV
$x > 0$	$x < 0$	$x$	$x$
$y > 0$	$y$	$y$	$y$

En los siguientes problemas, las gráficas de puntos se denominan diagramas de dispersión y frecuentemente son utilizadas por los estadísticos para determinar si existe una relación entre las dos variables en consideración. El primer componente del par ordenado se llama la variable de entrada y el segundo componente se llama la variable de salida. Construye los diagramas de dispersión. Determinar si parece existir una relación entre las dos variables bajo consideración haciendo las siguientes observaciones: Puede existir una relación si

a medida que aumenta una variable, la otra variable aumenta
a medida que aumenta una variable, la otra variable disminuye

Contestar

I	II	III	IV
$x > 0$	$x < 0$	$x < 0$	$x > 0$
$y > 0$	$y > 0$	$y < 0$	$y < 0$

Ejercicio$\PageIndex{6}$

Un psicólogo, al estudiar los efectos de un placebo en los trabajadores de la línea de montaje en un sitio industrial en particular, señaló el tiempo que tardó en ensamblar un determinado artículo antes de que se le diera el placebo al sujeto,$x$, y el tiempo que tardó en ensamblar un artículo similar después de que al sujeto se le diera el placebo,$y$. Los datos del psicólogo son

$x$	$y$
10	8
12	9
11	9
10	7
14	11
15	12
13	10

$Un plano de coordenadas xy sin líneas de rejilla. El eje x va a quince y el eje y va a doce. El eje x se rompe para comenzar a las diez y luego aumenta en un intervalo de una unidad. El eje y se rompe para comenzar a las seis y luego aumenta en un intervalo de doce.$

Ejercicio$\PageIndex{7}$

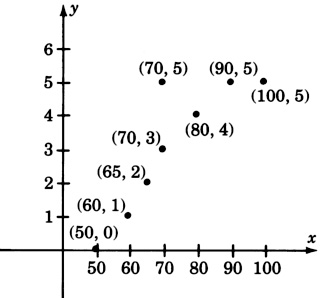
Los siguientes datos se obtuvieron en un estudio de ingeniería sobre la relación entre la cantidad de presión utilizada para formar una pieza de maquinaria$x$, y el número de piezas defectuosas de maquinaria producidas,$y$.

$x$	$y$
50	0
60	1
65	2
70	3
80	4
70	5
90	5
100	5

$Un plano de coordenadas xy sin líneas de rejilla. El eje x va a cien y el eje y va a seis. El eje x se rompe para comenzar a los cincuenta y luego aumenta en un intervalo de diez unidades. El eje y va a seis en incrementos de uno.$

Contestar

Sí, sí parece haber una relación.

$Total de ocho puntos trazados en un plano de coordenadas xy sin líneas de rejilla. El eje x va a cien y el eje y va a seis. El eje x comienza a los cincuenta y luego aumenta en un intervalo de diez unidades. El eje y va a seis en incrementos de uno. Las coordenadas de los puntos son cincuenta, cero; sesenta, uno; sesenta y cinco, dos; setenta, tres; setenta, cinco; ochenta, cuatro; noventa, cinco; y ciento cinco.$

Ejercicio$\PageIndex{8}$

Los siguientes datos representan el número de días de trabajo perdidos por año,$x$, por los empleados de una compañía de seguros y el número de minutos que llegan tarde del almuerzo,$y$.

$x$	$y$
1	3
6	4
2	2
2	3
3	1
1	4
4	4
6	3
5	2
6	1

$Un plano de coordenadas xy sin líneas de rejilla. El eje x va a siete en incrementos de uno y el eje y va a cinco en incrementos de uno.$

Ejercicio$\PageIndex{9}$

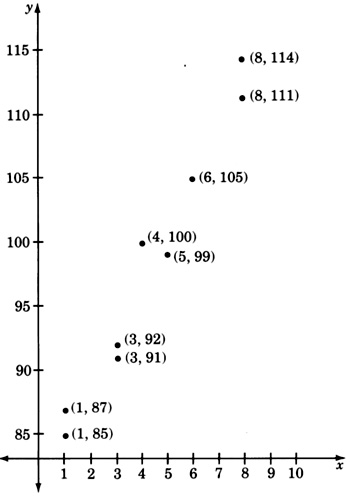
Un fabricante de equipo dental cuenta con los siguientes datos sobre el costo unitario (en dólares),$y$, de un artículo en particular y el número de unidades,$x$, fabricadas para cada pedido.

$x$	$y$
1	85
3	92
5	99
3	91
4	100
1	87
6	105
8	111
8	114

$Un plano de coordenadas xy sin líneas de rejilla. El eje x va a diez en incrementos de uno. El eje y se rompe para comenzar en ochenta y cinco e ir en incrementos de quince a partir de entonces, con la última etiqueta como ciento quince. El eje x va a diez en incrementos de uno.$

Contestar

Sí, sí parece haber una relación.

$Total de nueve puntos trazados en un plano de coordenadas xy sin líneas de rejilla. El eje x va a diez y el eje y va a ciento quince. El eje y comienza en ochenta y cinco y luego aumenta en un intervalo de cinco unidades. El eje x va a diez en incrementos de uno. Las coordenadas de los puntos son uno, ochenta y cinco; uno, ochenta y siete; tres, noventa y uno; tres, noventa y dos; cuatro, cien; cinco, noventa y nueve; seis, ciento cinco; ocho, ciento once; y ocho, ciento catorce.$

Ejercicios para la revisión

Ejercicio$\PageIndex{10}$

Simplificar$(\dfrac{18x^5y^6}{9x^2y^4})^5$

Ejercicio$\PageIndex{11}$

Suministrar la palabra faltante. An es una declaración de que dos expresiones algebraicas son iguales.

Contestar: ecuación

Ejercicio$\PageIndex{12}$

Simplifica la expresión$5xy(xy−2x+3y)−2xy(3xy−4x)−15xy^2$.

Ejercicio$\PageIndex{13}$

Identificar la ecuación$x + 2 = x + 1$ como una identidad, una contradicción o una ecuación condicional.

Contestar: contradicción

Ejercicio$\PageIndex{14}$

Suministrar la frase que falta. Un sistema de ejes construidos para graficar una ecuación se llama

I	II	III	IV
\(x > 0\)	\(x < 0\)	\(x\)	\(x\)
\(y > 0\)	\(y\)	\(y\)	\(y\)

I	II	III	IV
\(x > 0\)	\(x < 0\)	\(x < 0\)	\(x > 0\)
\(y > 0\)	\(y > 0\)	\(y < 0\)	\(y < 0\)

Search

Ejemplo\(\PageIndex{1}\)

Problema de práctica\(\PageIndex{1}\)

Ejercicio\(\PageIndex{1}\)

Ejercicio\(\PageIndex{2}\)

Ejercicio\(\PageIndex{3}\)

Ejercicio\(\PageIndex{4}\)

Ejercicio\(\PageIndex{5}\)

Ejercicio\(\PageIndex{6}\)

Ejercicio\(\PageIndex{7}\)

Ejercicio\(\PageIndex{8}\)

Ejercicio\(\PageIndex{9}\)

Ejercicio\(\PageIndex{10}\)

Ejercicio\(\PageIndex{11}\)

Ejercicio\(\PageIndex{12}\)

Ejercicio\(\PageIndex{13}\)

Ejercicio\(\PageIndex{14}\)