7.5: La forma de pendiente-interceptación de una línea
- Page ID
- 112284
La forma general de una línea
Hemos visto que la forma general de una ecuación lineal en dos variables es ax+por=c (Sección 7.4). Cuando esta ecuación se resuelve para y, la forma resultante se llama la forma pendiente-intercepción. Vamos a generar esta nueva forma.
\ (\ begin {alineado}
ax + por &=c&\ text {Restar} hacha\ texto {de ambos lados.}\\
por &= -ax + c&\ text {Divide ambos lados por} b
\\\ dfrac {por} {b} &=\ dfrac {-ax} {b} +\ dfrac {c} {b}
\\ dfrac {\ no b} y} {\ not {b}} &=\ dfrac {-ax} {b} +\ dfrac {c} { b}\\
y&=\ dfrac {-ax} {b} +\ dfrac {c} {b}\\
\ final {alineado}\)
Esta ecuación es de la forma\(y = mx + b\) si reemplazamos\(\dfrac{-a}{b}\) con\(m\) y constante\(\dfrac{c}{b}\) con\(b\). (Nota El hecho de que dejemos\(b = \dfrac{c}{b}\) es lamentable y ocurre por las letras que hemos optado por usar en la forma general. La letra\(b\) aparece en ambos lados del signo igual y puede no representar el mismo valor en absoluto. Este problema es una de las convenciones históricas y, afortunadamente, no ocurre muy a menudo).
Los siguientes ejemplos ilustran este procedimiento.
Resolver\(3x + 2y = 6\) para\(y\).
\ (\ begin {alineado}
3x + 2y&= 6&\ text {Restar} 3x\ texto {de ambos lados}\\
2y&= -3x + 6&\ text {Divide ambos lados por} 2\\
y &= -\ dfrac {3} {2} x + 3
\ end {alineado}\)
La ecuación es de la forma\(y = mx + b\). En este caso,\(m = -\dfrac{3}{2}\) y\(b = 3\).
Resolver\(-15x + 5y = 20\) para\(y\).
\ (\ comenzar {alineado}
-15x + 5y&=20\\
5y&=15x + 20\\
y&=3x+4
\ final {alineado}\)
Esta ecuación es de la forma\(y = mx + b\). En este caso,\(m = 3\) y\(b = 4\).
Resolver\(4x-y = 0\) para\(y\).
\ (\ begin {alineado}
4x-y&=0\\
-y&=-4x\\
y&=4x
\ end {alineado}\)
Esta ecuación es de la forma\(y = mx + b\). En este caso,\(m=4\) y\(b=0\). Observe que podemos escribir\(y=4x\) como\(y = 4x + 0\)
La forma pendiente-interceptación de una línea
La forma pendiente-intersección de una línea\(y=mx+b\)
Se dice que una ecuación lineal en dos variables escritas en la forma\(y=mx+b\) está en forma de pendiente-intercepción.
Conjunto de Muestras A
Las siguientes ecuaciones están en forma de pendiente-intersección:
\(y = 6x - 7\). En este caso\(m = 6\) y\(b = -7\)
\(y = -2x + 9\). En este caso\(m = -2\) y\(b = 9\)
\(y = \dfrac{1}{5}x + 4.8\). En este caso\(m = \dfrac{1}{5}\) y\(b = 4.8\)
\(y = 7x\). En este caso\(m = 7\) y\(b = 0\) ya que podemos escribir\(y = 7x\) como\(y = 7x + 0\).
Las siguientes ecuaciones no están en forma de pendiente-intersección.
\(2y = 4x - 1\). El coeficiente de\(y\) es\(2\). Para estar en forma pendiente-intercepción, el coeficiente de\(y\) debe ser\(1\).
\(y + 4x = 5\). La ecuación no está resuelta para\(y\). EL\(x\) y\(y\) aparecen en el mismo lado del signo igual.
\(y + 1 = 2x\). La ecuación no se resuelve para\(y\)
Conjunto de práctica A
Las siguientes ecuaciones están en forma de pendiente-intercepción. En cada caso, especifique la pendiente y\(y\) -interceptar.
\(y=2x+7; m=?, b=?\)
- Contestar
-
\(m=2, b=7\)
\(y=−4x+2; m=?, b=?\)
- Contestar
-
\(m=−4,b=2\)
\(y=−5x−1; m=?, b=?\)
- Contestar
-
\(m=−5,b=−1\)
\(y=\dfrac{2}{3}x−10; m=?, b=?\)
- Contestar
-
\(m = \dfrac{2}{3}, b = -10\)
\(y = \dfrac{-5}{8}x + \dfrac{1}{2}; m=?, b=?\)
- Contestar
-
\(m = \dfrac{-5}{8}, b=\dfrac{1}{2}\)
\(y=−3x; m=?, b=?\)
- Contestar
-
\(m=−3, b=0\)
Pendiente e Intercepción
Cuando la ecuación de una línea se escribe en forma de pendiente-intercepción, se pueden ver dos propiedades importantes de la línea: la pendiente y la intercepción. Veamos estas dos propiedades graficando varias líneas y observándolas cuidadosamente.
Conjunto de Muestras B
Grafica la línea\(y=x−3\).
| \(x\) | \(y\) | \((x, y)\) |
| \(0\) | \(−3\) | \((0, −3)\) |
| \(4\) | \(1\) | \((4, 1)\) |
| \(−2\) | \(−5\) | \((−2, −5)\) |
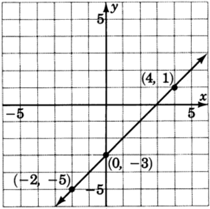
Mirando cuidadosamente esta línea, conteste las siguientes dos preguntas.
¿En qué número esta línea cruza el eje y? ¿Ves este número en la ecuación?
La línea cruza el eje y en −3.
Coloca tu lápiz en cualquier punto de la línea. Mueve tu lápiz exactamente una unidad horizontalmente hacia la derecha. Ahora bien, ¿cuántas unidades hacia arriba o hacia abajo debes mover tu lápiz para volver a la línea? ¿Ves este número en la ecuación?
Después de mover horizontalmente una unidad a la derecha, debemos mover exactamente una unidad vertical hacia arriba. Este número es el coeficiente de\(x\).
Grafica la línea\(y = \dfrac{2}{3}x + 1\)
| \(x\) | \(y\) | \((x, y)\) |
| \(0\) | \(1\) | \((0, 1)\) |
| \(3\) | \(3\) | \((3, 3)\) |
| \(−3\) | \(−1\) | \((−3, −1)\) |
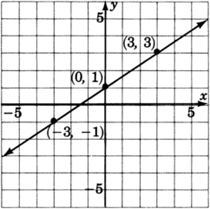
Mirando cuidadosamente esta línea, conteste las siguientes dos preguntas.
¿En qué número esta línea cruza el\(y\) eje -eje? ¿Ves este número en la ecuación?
La línea cruza el\(y\) eje -en\(+1\).
Coloca tu lápiz en cualquier punto de la línea. Mueve tu lápiz exactamente una unidad horizontalmente hacia la derecha. Ahora bien, ¿cuántas unidades hacia arriba o hacia abajo debes mover tu lápiz para volver a la línea? ¿Ves este número en la ecuación?
Después de mover horizontalmente una unidad a la derecha, debemos mover exactamente la\(\dfrac{2}{3}\) unidad hacia arriba. Este número es el coeficiente de\(x\).
Set de práctica B
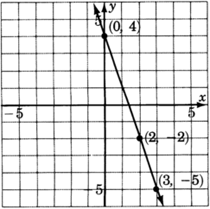
Grafica la línea\(y = -3x + 4\)
| \(x\) | \(y\) | \((x, y)\) |
| \(0\) | - | - |
| \(3\) | - | - |
| \(2\) | - | - |
Mirando cuidadosamente esta línea, conteste las siguientes dos preguntas.
¿En qué número cruza la línea el\(y\) eje -eje? ¿Ves este número en la ecuación?
- Contestar
-
La línea cruza el\(y\) eje -en\(+4\). Después de mover horizontalmente la\(1\) unidad hacia la derecha, debemos mover exactamente\(3\) las unidades hacia abajo.
Coloca tu lápiz en cualquier punto de la línea. Mueve tu lápiz exactamente una unidad horizontalmente hacia la derecha. Ahora bien, ¿cuántas unidades hacia arriba o hacia abajo debes mover tu lápiz para volver a la línea? ¿Ves este número en la ecuación?
- Contestar
-
En las gráficas construidas en el Conjunto de Muestras B y el Conjunto de Práctica B, cada ecuación tenía la forma\(y=mx+b\). Podemos responder las mismas preguntas usando esta forma de la ecuación (mostrada en el diagrama).
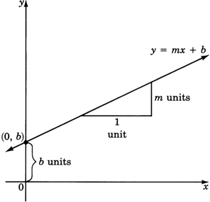
\(y\)-Interceptar
¿En qué número cruza la línea el\(y\) eje -eje? ¿Ves este número en la ecuación?
- Contestar
-
En cada caso, la línea cruza el\(y\) eje -en la constante\(b\). El número\(b\) es el número en el que la línea cruza el\(y\) eje -y se llama la\(y\) -intercepción. El par ordenado correspondiente a la\(y\) -intercepción es\((0, b)\).
Coloca tu lápiz en cualquier punto de la línea. Mueve tu lápiz exactamente una unidad horizontalmente hacia la derecha. Ahora bien, ¿cuántas unidades hacia arriba o hacia abajo debes mover tu lápiz para volver a la línea? ¿Ves este número en la ecuación?
- Contestar
-
Para volver a la línea, debemos mover nuestro lápiz exactamente unidades\(m\) verticales.
Talud
El número\(m\) es el coeficiente de la variable\(x\). El número\(m\) se llama pendiente de la línea y es el número de unidades que\(y\) cambia cuando\(x\) se incrementa por\(1\) unidad. Por lo tanto, si\(x\) cambia por\(1\) unidad,\(y\) cambia por\(m\) unidades.
Dado que la ecuación\(y=mx+b\) contiene tanto la pendiente de la línea como la\(y\) intersección, llamamos a la forma\(y=mx+b\) la forma pendiente-intercepción.
La forma pendiente-intercepción de una línea recta es\(y=mx+b\)
La pendiente de la línea es\(m\), y la\(y\) -intercepción es el punto\((0 , b)\).
La Pendiente es una Medida de la Inclinación de una Línea
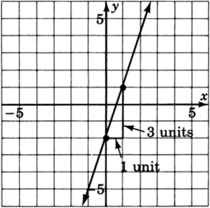
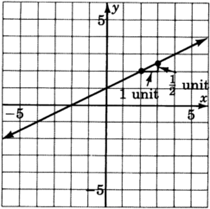
La palabra pendiente es realmente bastante apropiada. Nos da una medida de la pendiente de la línea. Considera dos líneas, una con pendiente\(\dfrac{1}{2}\) y la otra con pendiente\(3\). La línea con pendiente\(3\) es más pronunciada que la línea con pendiente\(\dfrac{1}{2}\). Imagina que tu lápiz se coloca en cualquier punto de las líneas. Hacemos un incremento de\(1\) -unidad en el\(x\) -valor moviendo el lápiz una unidad hacia la derecha. Para volver a una línea solo necesitamos movernos verticalmente\(\dfrac{1}{2}\) unidad, mientras que para volver a la otra línea necesitamos mover\(3\) unidades verticalmente.
Conjunto de Muestras C
Encuentra la pendiente y la intersección y de las siguientes líneas.
\(y = 2x + 7\)
La línea está en forma de pendiente-intercepción\(y=mx+b\). La pendiente es\(m\), el coeficiente de\(x\). Por lo tanto,\(m=2\). El\(y\) -intercepto es el punto\((0, b)\). Ya que\(b=7\), la\(y\) -intercepción es\((0, 7)\).
Pendiente:\(2\)
\(y\)-interceptar:\((0, 7)\)
\(y = -4x + 1\)
La línea está en forma de pendiente-intercepción\(y=mx+b\). La pendiente es\(m\), el coeficiente de\(x\). Por lo tanto,\(m=-4\). El\(y\) -intercepto es el punto\((0, b)\). Ya que\(b=1\), la\(y\) -intercepción es\((0, 1)\).
Pendiente:\(-4\)
\(y\)-interceptar:\((0, 1)\)
\(3x + 2y = 5\).
Esta ecuación está escrita en forma general. Podemos poner la ecuación en forma de pendiente-intercepción resolviendo para\(y\).
\ (\ begin {alineado}
3x+2y&=5\\
2y&=-3x+5\
y&=-\ dfrac {3} {2} x +\ dfrac {5} {2}
\ end {alineado}\)
Ahora la ecuación está en forma de pendiente-intercepción.
Pendiente:\(-\dfrac{3}{2}\)
\(y\)-interceptar:\((0, \dfrac{5}{2})\)
Set de práctica C
Encuentra la pendiente y\(y\) -intercepción de la línea\(2x+5y=15\).
- Contestar
-
Resolviendo para\(y\) nosotros conseguimos\(y = \dfrac{-2}{5}x + 3\). Ahora\(m = \dfrac{-2}{5}\) y\(b = 3\).
La fórmula para la pendiente de una línea
Hemos observado que la pendiente es una medida de la inclinación de una línea. Deseamos desarrollar una fórmula para medir esta pendiente.
Parece razonable desarrollar una fórmula de pendiente que produzca los siguientes resultados:
Inclinación de la\(1>\) pendiente de línea de la línea 2.
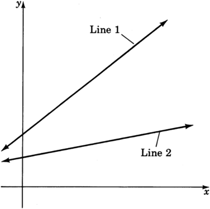
Considera una línea en la que seleccionamos dos puntos cualesquiera. Denotaremos estos puntos con los pares ordenados\((x_1, y_1 )\) y\((x_2, y_2 )\). Los subíndices nos ayudan a identificar los puntos.
\((x_1, y_1)\)es el primer punto. El subíndice\(1\) indica el primer punto.
\((x_2, y_2)\)es el segundo punto. El subíndice\(2\) indica el segundo punto.
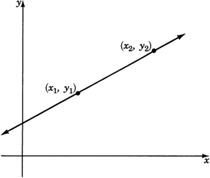
La diferencia de\(x\) valores nos\((x_2−x_1)\) da el cambio horizontal, y la diferencia de\(y\) valores nos\((y_2−y_1)\) da el cambio vertical. Si la línea es muy empinada, entonces al ir del primer punto al segundo punto, esperaríamos un gran cambio vertical en comparación con el cambio horizontal. Si la línea no es muy empinada, entonces al ir del primer punto al segundo punto, esperaríamos un pequeño cambio vertical en comparación con el cambio horizontal.
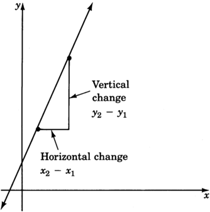
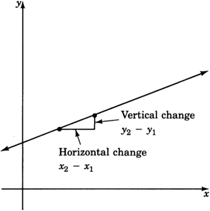
Estamos comparando cambios. Vemos que estamos comparando:
\ (\ begin {alineado}
\ text {El cambio vertical} &\ text {a} &\ text {el cambio horizontal}\\
\ text {El cambio en} y&\ text {a} &\ text {el cambio en} x\
y_1-y_1&\ text {a} &x_2-x_1
\ end {alineado}\)
Esto es una comparación y por lo tanto es una relación. Las relaciones se pueden expresar como fracciones. Así, una medida de la inclinación de una línea se puede expresar como una relación.
La pendiente de una línea se define como la relación
\(\text{Slope } = \dfrac{\text{ change in } y}{\text{ change in } x}\)
Matemáticamente, podemos escribir estos cambios como
\(\text{Slope } = \dfrac{y_2-y_1}{x_2-x_1}\)
La pendiente de una línea no vertical que pasa por los puntos\((x_1, y_1)\) y\((x_2, y_2)\) se encuentra mediante la fórmula:
\(m = \dfrac{y_2 - y_1}{x_2 - x_1}\)
Conjunto de Muestras D
Para los dos puntos dados, encuentra la pendiente de la línea que pasa por ellos.
\((0,1)\)y\((1,3)\).
Mirando de izquierda a derecha en la línea podemos\((x_1, y_1)\) elegir ser\((0,1)\), y\((x_2, y_2)\) ser\((1, 3)\). Entonces,
\(m = \dfrac{y_2-y_1}{x_2-x_1} = \dfrac{3-1}{1-0} = \dfrac{2}{1} = 2\)
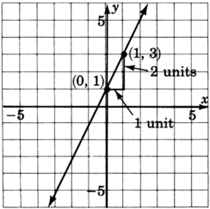
Esta línea tiene pendiente\(2\). Parece bastante empinado. Cuando la pendiente se escribe en forma de fracción,\(2 = \dfrac{2}{1}\), podemos ver, recordando la fórmula de pendiente, que a medida que\(x\) cambia\(1\) unidad a la derecha (debido a la\(+1\))\(y\) cambia\(2\) unidades hacia arriba (debido a la\(+2\).
\(m = \dfrac{\text{ change in } y}{\text{ change in } x} = \dfrac{2}{1}\).
Observe que a medida que miramos de izquierda a derecha, la línea sube.
\((2,2)\)y\((4,3)\).
Mirando de izquierda a derecha en la línea podemos\((x_1, y_1)\) elegir ser\((2,2)\), y\((x_2, y_2)\) ser\((4, 3)\). Entonces,
\(m = \dfrac{y_2-y_1}{x_2-x_1} = \dfrac{3-2}{4-2} = \dfrac{1}{2}\)
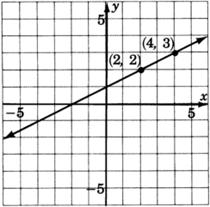
Esta línea tiene pendiente\(\dfrac{1}{2}\). Así, a medida que\(x\) cambia\(2\) unidades a la derecha (debido a la\(+2\),\(y\) cambia\(1\) unidad hacia arriba (debido a la\(+1\)).
\(m = \dfrac{\text{ change in } y}{\text{ change in } x} = \dfrac{1}{2}\).
Observe que en los ejemplos 16 y 17, ambas líneas tienen pendientes positivas,\(+2\) y\(+\dfrac{1}{2}\), y ambas líneas se elevan a medida que miramos de izquierda a derecha.
\((-2, 4)\)y\((1,1)\).
Mirando de izquierda a derecha en la línea podemos\((x_1, y_1)\) elegir ser\((-2,4)\), y\((x_2, y_2)\) ser\((1,1)\). Entonces,
\(m = \dfrac{y_2-y_1}{x_2-x_1} = \dfrac{1-4}{1-(-2)} = \dfrac{-3}{1 + 2} = \dfrac{-3}{3} = -1\)
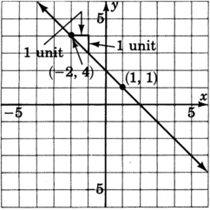
Esta línea tiene pendiente\(-1\).
Cuando la pendiente se escribe en forma de fracción,\(m = -1 = \dfrac{-1}{+1}\), podemos ver que a medida que\(x\) cambia\(1\) unidad a la derecha (debido a la\(+1\),\(y\) cambia\(1\) unidad hacia abajo (debido a la\(-1\)).
Observe también que esta línea tiene una pendiente negativa y disminuye a medida que miramos de izquierda a derecha.
\((1, 3)\)y\((5, 3)\).
\(m = \dfrac{y_2-y_1}{x_2-x_1} = \dfrac{3-3}{5-1} = \dfrac{0}{4} = 0\)
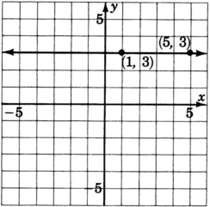
Esta línea tiene\(0\) pendiente. Esto quiere decir que no tiene subida y, por lo tanto, es una línea horizontal. Esto no quiere decir que la línea no tenga pendiente, sin embargo.
\((4,4)\)y\((4,0)\).
\(m = \dfrac{y_2-y_1}{x_2-x_1} = \dfrac{0-4}{4-4} = \dfrac{-4}{0}\)
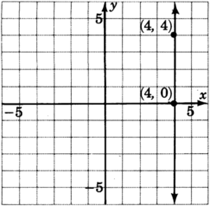
Dado que la división por\(0\) es indefinida, decimos que las líneas verticales tienen pendiente indefinida. Como no hay un número real que represente la pendiente de esta línea, a veces decimos que las líneas verticales tienen pendiente indefinida, o ninguna pendiente.
Set de Práctica D
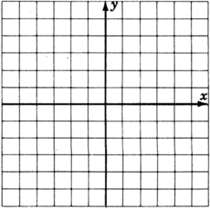
Encuentra la pendiente de la línea que pasa por\((2,1)\) y\((6,3)\). Grafica esta línea en la gráfica del problema 2 a continuación.
- Contestar
-
\(m = \dfrac{3-1}{6-2} = \dfrac{2}{4} = \dfrac{1}{2}\)
Encuentra la pendiente de la línea que pasa por\((3,4)\) y\((5,5)\). Grafica esta línea.
- Contestar
-
La línea tiene pendiente\(\dfrac{1}{2}\)
Compara las líneas de los siguientes problemas. ¿Las líneas parecen cruzarse? ¿Cómo se llama cuando las líneas no se encuentran (paralelas o intersectadas)? Compara sus pendientes. Hacer una declaración sobre el estado de estas líneas y sus pendientes.
- Contestar
-
Las líneas parecen ser paralelas. Las líneas paralelas tienen la misma pendiente, y las líneas que tienen la misma pendiente son paralelas
Antes de intentar algunos problemas, resumimos lo que hemos observado.
- La ecuación\(y=mx+b\) se llama la forma pendiente-intersección de la ecuación de una línea. El número\(m\) es la pendiente de la línea y el punto\((0,b)\) es la\(y\) -intercepción.
- La pendiente,\(m\), de una línea se define como la inclinación de la línea, y es el número de unidades que\(y\) cambia cuando\(x\) cambia de\(1\) unidad.
- La fórmula para encontrar la pendiente de una línea a través de dos puntos dados\((x_1,y_1)\) y\((x_2,y_2)\) es:
- \(m = \dfrac{y_2-y_1}{x_2-x_1}\)
- La fracción\(\dfrac{y_2-y_1}{x_2-x_1}\) representa el\ dfrac {\ text {cambio en} y} {\ text {cambio en} x}
- Al observar una gráfica de izquierda a derecha, las líneas con pendiente positiva suben y las líneas con pendiente negativa disminuyen.
- Las líneas paralelas tienen la misma pendiente.
- Las líneas horizontales tienen pendiente 0.
- Las líneas verticales tienen pendiente indefinida (o ninguna pendiente).
Ejercicios
Para los siguientes problemas, determinar la pendiente y la intersección en y de las líneas.
\(y=3x+4\)
- Contestar
-
pendiente =\(3\);\(y\) -intercept=\((0,4)\)
\(y=2x+9\)
\(y=9x+1\)
- Contestar
-
pendiente =\(9\);\(y\) -intercept=\((0,1)\)
\(y=7x+10\)
\(y=−4x+5\)
- Contestar
-
pendiente =\(-4\);\(y\) -intercept=\((0,5)\)
\(y=−2x+8\)
\(y=−6x−1\)
- Contestar
-
pendiente =\(-6\);\(y\) -intercept=\((0,-1)\)
\(y=−x−6\)
\(y=−x+2\)
- Contestar
-
pendiente =\(-1\);\(y\) -intercept=\((0,2)\)
\(2y=4x+8\)
\(4y=16x+20\)
- Contestar
-
pendiente =\(4\);\(y\) -intercept=\((0,5)\)
\(−5y=15x+55\)
\(−3y=12x−27\)
- Contestar
-
pendiente =\(-4\);\(y\) -intercept=\((0,9)\)
\(y = \dfrac{3}{5} - 8\)
\(y = \dfrac{2}{7} - 12\)
- Contestar
-
pendiente =\(\dfrac{2}{7}\);\(y\) -intercept=\((0,-12)\)
\(y = \dfrac{-1}{8}x + \dfrac{2}{3}\)
\(y = \dfrac{-4}{5} - \dfrac{4}{7}\)
- Contestar
-
pendiente =\(-\dfrac{4}{5}\);\(y\) -intercept=\((0,-\dfrac{4}{7})\)
\(−3y=5x+8\)
\(−10y=−12x+1\)
- Contestar
-
pendiente =\(\dfrac{6}{5}\);\(y\) -intercept=\((0,-\dfrac{1}{10})\)
\(−y=x+1\)
\(−y=−x+3\)
- Contestar
-
pendiente =\(1\);\(y\) -intercept=\((0,-3)\)
\(3x−y=7\)
\(5x+3y=6\)
- Contestar
-
pendiente =\(-\dfrac{5}{3}\);\(y\) -intercept=\((0,2)\)
\(−6x−7y=−12\)
\(−x+4y=−1\)
- Contestar
-
pendiente =\(\dfrac{1}{4}\);\(y\) -intercept=\((0,-\dfrac{1}{4})\)
Para los siguientes problemas, encuentra la pendiente de la línea a través de los pares de puntos.
\((1, 6), (4,9)\)
\((1, 3), (4,7)\)
- Contestar
-
\(m = \dfrac{4}{3}\)
\((3, 5), (4,7)\)
\((6, 1), (2,8)\)
- Contestar
-
\(m = -\dfrac{7}{4}\)
\((0, 5), (2,−6)\)
\((−2, 1), (0,5)\)
- Contestar
-
\(m=2\)
\((3, −9), (5,1)\)
\((4, −6), (−2,1)\)
- Contestar
-
\(m = -\dfrac{7}{6}\)
\((−5, 4), (−1,0)\)
\((−3, 2), (−4,6)\)
- Contestar
-
\(m=−4\)
\((9, 12), (6,0)\)
\((0, 0), (6,6)\)
- Contestar
-
\(m=1\)
\((−2, −6), (−4,−1)\)
\((−1, −7), (−2,−9)\)
- Contestar
-
\(m=2\)
\((−6, −6), (−5,−4)\)
\((−1, 0), (−2,−2)\)
- Contestar
-
\(m=2\)
\((−4, −2), (0,0)\)
\((2, 3), (10,3)\)
- Contestar
-
\(m=0\)(línea horizontal\(y=3\))
Hacer una declaración sobre las pendientes de las líneas paralelas.
\((4, −2), (4,7)\)
\((8, −1), (8,3)\)
- Contestar
-
Sin pendiente (línea vertical en\(x=8\))
\((4, 2), (6,2)\)
\((5, −6), (9,−6)\)
- Contestar
-
\(m=0\)(línea horizontal en\(y=−6\))
¿Las líneas con pendiente positiva suben o bajan a medida que miramos de izquierda a derecha?
¿Las líneas con pendiente negativa suben o bajan a medida que miramos de izquierda a derecha?
- Contestar
-
declinar
Para los siguientes problemas, determinar la pendiente y la intersección en y de las líneas. Redondear a dos decimales.
\(3.8x+12.1y=4.26\)
- Contestar
-
pendienta=\(−0.31\)
\(y\)−intercept=\((0,0.35)\)
\(8.09x+5.57y=−1.42\)
\(10.813x−17.0y=−45.99\)
- Contestar
-
pendienta=\(0.64\)
\(y\)−intercept=\((0,2.71)\)
\(−6.003x−92.388y=0.008\)
Para los siguientes problemas, encuentra la pendiente de la línea a través de los pares de puntos. Redondear a dos decimales.
\((5.56, 9.37), (2.16, 4.90)\)
- Contestar
-
\(m=1.31\)
\((33.1, 8.9), (42.7, −1.06)\)
\((155.89, 227.61), (157.04,227.61)\)
- Contestar
-
\(m=0\)(línea horizontal en\(y=227.61\))
\((0.00426, −0.00404), (−0.00191, −0.00404)\)
\((88.81, −23.19), (88.81, −26.87)\)
- Contestar
-
Sin pendiente (línea vertical\(x=88.81\))
\((−0.0000567, −0.0000567), (−0.00765, 0.00764)\)
Ejercicios para la revisión
Simplificar\((x^2y^3w^4)^0\).
- Contestar
-
\(1\)si\(xyw≠0\)
Resuelve la ecuación\(3x−4(2−x)−3(x−2)+4=0\).
Cuando cuatro veces un número se divide por cinco, y ese resultado se disminuye en ocho, el resultado es cero. ¿Cuál es el número original?
- Contestar
-
\(10\)
Resolver\(−3y+10=x+2\) si\(x=−4\).
Grafica la ecuación lineal\(x+y=3\).
- Contestar
-