7.6: Graficar ecuaciones en forma de pendiente-intercepción

Última actualización
Guardar como PDF

Page ID: 112312

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Uso de la pendiente y la intercepción para graficar una línea

Cuando se da una ecuación lineal en la forma general,$ax+by=c$, observamos que un enfoque gráfico eficiente fue el método de intercepción. Dejamos$x=0$ y calculamos el valor correspondiente de$y$, luego let$y=0$ y calculamos el valor correspondiente de$x$.

Cuando una ecuación se escribe en la forma pendiente-intercepción$y=mx+b$,, también hay formas eficientes de construir la gráfica. Una forma, pero menos eficiente, es elegir dos o tres$x$ valores y calcular para encontrar los$y$ valores correspondientes. Sin embargo, los cálculos son tediosos, consumen mucho tiempo y pueden generar errores. Otra forma, el método que se indica a continuación, hace uso de la pendiente y la$y$ -intercepción para graficar la línea. Es rápido, sencillo y no implica cálculos.

Método de graficación

Trazar la$y$ -intercepción$(0, b)$.
Determinar otro punto usando la pendiente m.
Dibuja una línea a través de los dos puntos.

Recordemos que definimos la pendiente$m$ como la relación$\dfrac{y_2-y_1}{x_2-x_1}$. El numerador$y_2−y_1$ representa el número de unidades que$y$ cambia y el denominador$x_2 - x_1$ representa el número de unidades que$x$ cambia. Supongamos$m=pq$. Entonces$p$ es el número de unidades que$y$ cambia y$q$ es el número de unidades que$x$ cambia. Dado que estos cambios ocurren simultáneamente, comience con su lápiz en la$y$ -intercepción, mueva$p$ las unidades en la dirección vertical apropiada y luego mueva$q$ las unidades en la dirección horizontal apropiada. Marcar un punto en esta ubicación.

Conjunto de Muestras A

Grafica las siguientes líneas.

Ejemplo$\PageIndex{1}$

$y = \dfrac{3}{4}x + 2$

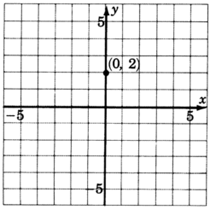
1. El$y$ -intercepto es el punto$(0,2)$. Así, la línea cruza las$2$ unidades$y$ del eje por encima del origen. Marcar un punto en$(0,2)$.

$Un plano de coordenadas xy con líneas de cuadrícula de cinco a cinco negativas en incrementos de una unidad para ambos ejes. El punto cero, dos se traza y se etiqueta en la cuadrícula.$

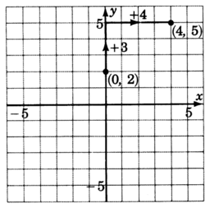
2. La pendiente,$m$, es$\dfrac{3}{4}$. Esto significa que si empezamos en algún punto de la línea y movemos nuestras$3$ unidades de lápiz hacia arriba y luego$4$ las unidades a la derecha, volveremos a estar en la línea. Empezar en un punto conocido, la$y$ -intercepción$(0, 2)$. Mueva$3$ las unidades hacia arriba, luego mueva$4$ las unidades a la derecha. Marcar un punto en esta ubicación. (Tenga en cuenta también que\ dfrac {3} {4} =\ dfrac {-3} {-4}\). Esto significa que si empezamos en algún punto de la línea y movemos nuestras$3$ unidades de lápiz hacia abajo y$4$ las unidades a la izquierda, volveremos a estar en la línea. Tenga en cuenta también eso$\dfrac{3}{4} = \dfrac{\dfrac{3}{4}}{1}$. Esto significa que si empezamos en algún punto de la línea y nos movemos a la$1$ unidad derecha, tendremos que subir$\dfrac{3}{4}$ unidad para volver a la línea.)

$Comenzando en punto con coordenadas cero, dos mueven tres unidades hacia arriba y cuatro unidades a la derecha para llegar al punto con las coordenadas cuatro, cinco.$

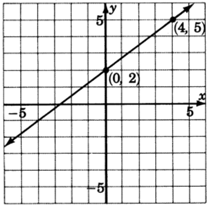
3. Dibuja una línea a través de ambos puntos.

$Gráfica de una línea que pasa por dos puntos con coordenadas cero, dos, y cuatro, cinco.$

Ejemplo$\PageIndex{2}$

$y = -\dfrac{1}{2}x + \dfrac{7}{2}$

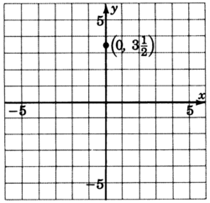
1. El$y$ -intercepto es el punto$(0, \dfrac{7}{2})$. Así, la línea cruza las$\dfrac{7}{2}$ unidades$y$ del eje por encima del origen. Marcar un punto$(0, \dfrac{7}{2})$, o$(0, 3\dfrac{1}{2})$.

$Un plano de coordenadas xy con líneas de cuadrícula de cinco a cinco negativas e incrementos de una unidad para ambos ejes. Se traza y etiqueta el punto cero, tres y medio.$

2. La pendiente,$m$, es$-\dfrac{1}{2}$. Podemos escribir$-\dfrac{1}{2}$ como$\dfrac{-1}{2}$. Así, partimos en un punto conocido, la$y$ -intercepción$(0, 3\dfrac{1}{2})$, nos desplazamos hacia abajo una unidad (debido a la$-1$), luego movemos$2$ las unidades a la derecha. Marcar un punto en esta ubicación.

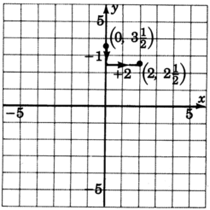
$Comenzando en punto con coordenadas cero, tres y media mueven una unidad hacia abajo y dos unidades a la derecha para llegar al punto con las coordenadas dos, dos y media.$

3. Dibuja una línea a través de ambos puntos.

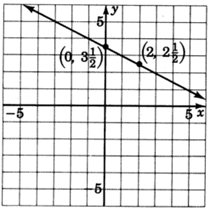
$Gráfica de una línea que pasa por dos puntos con coordenadas cero, tres y medio; y dos, dos y medio.$

Ejemplo$\PageIndex{3}$

$y = \dfrac{2}{5}x$

1. Podemos poner esta ecuación en pendiente-intercepción explícita escribiéndola como$y = \dfrac{2}{5}x + 0$.

El$y$ -intercepto está en el punto$(0, 0)$, el origen. Esta línea va justo por el origen.

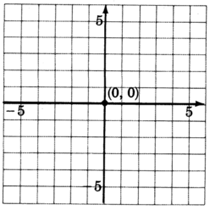
$Un plano de coordenadas xy con líneas de cuadrícula de cinco a cinco negativas e incrementos de una unidad para ambos ejes. El origen se etiqueta con el par de coordenadas cero, cero.$

2. La pendiente,$m$, es$\dfrac{2}{5}$. Comenzando por el origen, subimos$2$ unidades, luego nos movemos a las$5$ unidades correctas. Marcar un punto en esta ubicación.

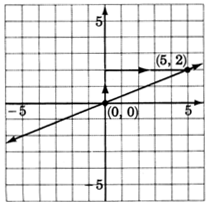
$Una gráfica de una línea que pasa por dos puntos con coordenadas cero, cero; y cinco, dos. Comenzando en un punto con coordenadas cero, cero mueve dos unidades hacia arriba y cinco unidades a la derecha para llegar al punto con las coordenadas cinco, dos.$

3. Dibuja una línea a través de los dos puntos.

Ejemplo$\PageIndex{4}$

$y = 2x - 4$

1. El$y$ -intercepto es el punto$(0, -4)$. Así, la línea cruza las$4$ unidades$y$ del eje por debajo del origen. Marcar un punto en$(0, -4)$.

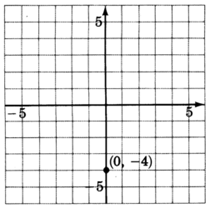
$Un punto con las coordenadas cero, negativo cuatro trazadas en un plano xy.$

2. La pendiente,$m$, es$2$. Si escribimos la pendiente como una fracción$2 = \dfrac{2}{1}$,, podemos leer cómo hacer los cambios. Comience en el punto conocido$(0, -4)$, mueva hacia arriba$2$ las unidades, luego mueva la$1$ unidad derecha. Marcar un punto en esta ubicación.

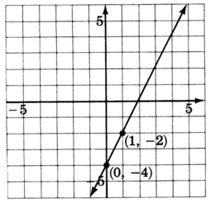
$Una gráfica de una línea que pasa por dos puntos con coordenadas cero, negativo cuatro y uno, negativo dos.$

3. Dibuja una línea a través de los dos puntos.

Conjunto de práctica A

Utilice la$y$ -intercepción y la pendiente para graficar cada línea.

Problema de práctica$\PageIndex{1}$

$y = \dfrac{-2}{3} + 4$

$Un plano xy con líneas de cuadrícula, etiquetadas como cinco y cinco negativas e incrementos de una unidad para ambos ejes.$

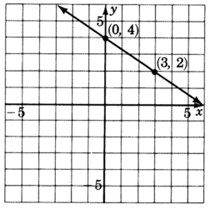
Responder: $Una gráfica de una línea que pasa por dos puntos con coordenadas cero, cuatro y tres, dos.$

Problema de práctica$\PageIndex{2}$

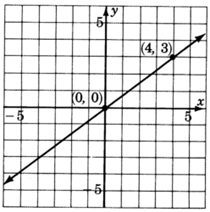
$y = \dfrac{3}{4}x$

$Un plano xy con líneas de cuadrícula, etiquetado negativo cinco y cinco en ambos ejes.$

Responder: $Una gráfica de una línea que pasa por dos puntos con las coordenadas cero, cero y cuatro, tres.$

Ejercicios

Para los siguientes problemas, grafica las ecuaciones.

Ejercicio$\PageIndex{1}$

$y = \dfrac{2}{3} + 1$

$Un plano xy con líneas de cuadrícula, etiquetado negativo cinco y cinco en ambos ejes.$

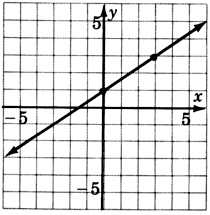
Responder: $Una gráfica de una línea que pasa por dos puntos con coordenadas cero, uno y tres, tres.$

Ejercicio$\PageIndex{2}$

$y = \dfrac{1}{4}x - 2$

$Un plano xy con líneas de cuadrícula, etiquetado negativo cinco y cinco en ambos ejes.$

Ejercicio$\PageIndex{3}$

$y = 5x - 4$

$Un plano xy con líneas de cuadrícula, etiquetado negativo cinco y cinco en ambos ejes.$

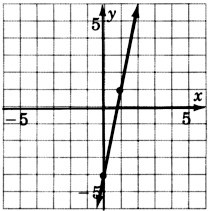
Responder: $Una gráfica de una línea que pasa por dos puntos con coordenadas cero, negativo cuatro y uno, uno.$

Ejercicio$\PageIndex{4}$

$y = -\dfrac{6}{5} - 3$

$Un plano xy con líneas de cuadrícula, etiquetado negativo cinco y cinco en ambos ejes.$

Ejercicio$\PageIndex{5}$

$y = \dfrac{3}{2} - 5$

$Un plano xy con líneas de cuadrícula, etiquetado negativo cinco y cinco en ambos ejes.$

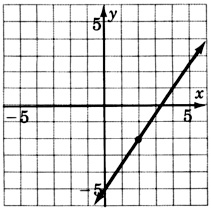
Responder: $Una gráfica de una línea que pasa por dos puntos con coordenadas cero, negativo cinco y dos, negativo dos.$

Ejercicio$\PageIndex{6}$

$y = \dfrac{1}{5}x + 2$

$Un plano xy con líneas de cuadrícula, etiquetado negativo cinco y cinco en ambos ejes.$

Ejercicio$\PageIndex{7}$

$y = -\dfrac{8}{3} + 4$

$Un plano xy con líneas de cuadrícula, etiquetado negativo cinco y cinco en ambos ejes.$

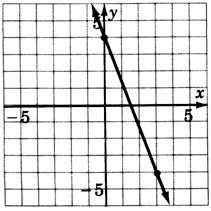
Responder: $Gráfica de una línea que pasa por dos puntos con coordenadas cero, cuatro y tres, cuatro negativas.$

Ejercicio$\PageIndex{8}$

$y = -\dfrac{10}{3} + 6$

$Un plano xy con líneas de cuadrícula, etiquetado negativo cinco y cinco en ambos ejes.$

Ejercicio$\PageIndex{9}$

$y = 1x - 4$

$Un plano xy con líneas de cuadrícula, etiquetado negativo cinco y cinco en ambos ejes.$

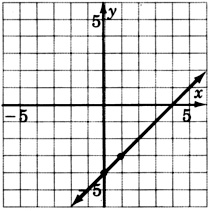
Responder: $Una gráfica de una línea que pasa por dos puntos con coordenadas cero, negativo cuatro y uno, negativo tres.$

Ejercicio$\PageIndex{10}$

$y = -2x + 1$

$Un plano xy con líneas de cuadrícula, etiquetado negativo cinco y cinco en ambos ejes.$

Ejercicio$\PageIndex{11}$

$y = x + 2$

$Un plano xy con líneas de cuadrícula, etiquetado negativo cinco y cinco en ambos ejes.$

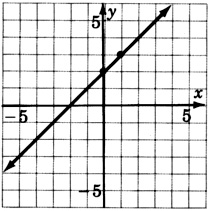
Responder: $Una gráfica de una línea que pasa por dos puntos con coordenadas cero, dos y uno, tres.$

Ejercicio$\PageIndex{12}$

$y = \dfrac{3}{5}x$

$Un plano xy con líneas de cuadrícula, etiquetado negativo cinco y cinco en ambos ejes.$

Ejercicio$\PageIndex{13}$

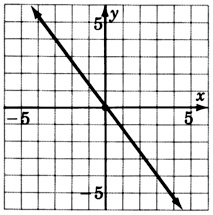
$y = -\dfrac{4}{3}$

$Un plano xy con líneas de cuadrícula, etiquetado negativo cinco y cinco en ambos ejes.$

Responder: $Una gráfica de una línea que pasa por dos puntos con las coordenadas cero, cero y negativo tres, cuatro.$

Ejercicio$\PageIndex{14}$

$y = x$

$Un plano xy con líneas de cuadrícula, etiquetado negativo cinco y cinco en ambos ejes.$

Ejercicio$\PageIndex{15}$

$y = -x$

$Un plano xy con líneas de cuadrícula, etiquetado negativo cinco y cinco en ambos ejes.$

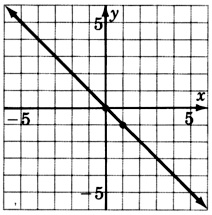
Responder: $Una gráfica de una línea que pasa por dos puntos con las coordenadas cero, cero y uno, uno negativo.$

Ejercicio$\PageIndex{16}$

$3y−2x=−3$

$Un plano xy con líneas de cuadrícula, etiquetado negativo cinco y cinco en ambos ejes.$

Ejercicio$\PageIndex{17}$

$6x+10y=30$

$Un plano xy con líneas de cuadrícula, etiquetado negativo cinco y cinco en ambos ejes.$

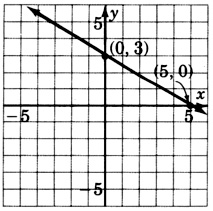
Responder: $Una gráfica de una línea que pasa por dos puntos con coordenadas cero, tres y cinco, cero.$

Ejercicio$\PageIndex{18}$

$x+y=0$

$Un plano xy con líneas de cuadrícula, etiquetado negativo cinco y cinco en ambos ejes.$

Ejercicios para revisión

Ejercicio$\PageIndex{19}$

Resolver la desigualdad$2 - 4x \ge x - 3$

Responder: $x≤1$

Ejercicio$\PageIndex{20}$

Graficar la desigualdad$y+3>1.$

$Una línea horizontal con flechas en ambos extremos.$

Ejercicio$\PageIndex{21}$

Grafica la ecuación$y = -2$.

$Un plano xy con líneas de cuadrícula, etiquetado negativo cinco y cinco en ambos ejes.$

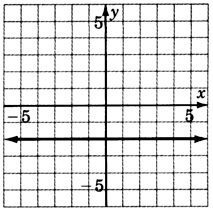
Responder: $Un gráfico de una línea paralela al eje x en un plano xy. La línea cruza el eje y en y es igual a dos negativos.$

Ejercicio$\PageIndex{22}$

Determinar la pendiente y$y$ -intercepción de la línea$−4y−3x=16$.

Ejercicio$\PageIndex{23}$

Encuentra la pendiente de la línea que pasa por los puntos$(−1, 5)$ y$(2, 3)$.

Responder: $m = \dfrac{-2}{3}$

Search

Método de graficación

Ejemplo\(\PageIndex{1}\)

Ejemplo\(\PageIndex{2}\)

Ejemplo\(\PageIndex{3}\)

Ejemplo\(\PageIndex{4}\)

Problema de práctica\(\PageIndex{1}\)

Problema de práctica\(\PageIndex{2}\)

Ejercicio\(\PageIndex{1}\)

Ejercicio\(\PageIndex{2}\)

Ejercicio\(\PageIndex{3}\)

Ejercicio\(\PageIndex{4}\)

Ejercicio\(\PageIndex{5}\)

Ejercicio\(\PageIndex{6}\)

Ejercicio\(\PageIndex{7}\)

Ejercicio\(\PageIndex{8}\)

Ejercicio\(\PageIndex{9}\)

Ejercicio\(\PageIndex{10}\)

Ejercicio\(\PageIndex{11}\)

Ejercicio\(\PageIndex{12}\)

Ejercicio\(\PageIndex{13}\)

Ejercicio\(\PageIndex{14}\)

Ejercicio\(\PageIndex{15}\)

Ejercicio\(\PageIndex{16}\)

Ejercicio\(\PageIndex{17}\)

Ejercicio\(\PageIndex{18}\)

Ejercicio\(\PageIndex{19}\)

Ejercicio\(\PageIndex{20}\)

Ejercicio\(\PageIndex{21}\)

Ejercicio\(\PageIndex{22}\)

Ejercicio\(\PageIndex{23}\)