7.7: Encontrar la ecuación de una línea
- Page ID
- 112330
Las formas de pendiente-intercepción y punto-pendiente
En los apartados anteriores se nos ha dado una ecuación y hemos construido la línea a la que corresponde. Ahora, sin embargo, supongamos que se nos da alguna información geométrica sobre la línea y deseamos construir la ecuación correspondiente. Deseamos encontrar la ecuación de una línea.
Sabemos que la fórmula para la pendiente de una línea es\(m - \dfrac{y_2 - y_1}{x_2-x_1}\). Podemos encontrar la ecuación de una línea usando la fórmula de pendiente de cualquiera de dos maneras:
Si se nos da la pendiente\(m\), y cualquier punto\((x_1, y_1)\) de la línea, podemos sustituir esta información en la fórmula para pendiente.
Dejar\((x_1, y_1)\) ser el punto conocido en la línea y dejar\((x,y)\) ser cualquier otro punto en la línea. Entonces
\ (\ begin {aligned}
m&=\ dfrac {y-y_1} {x-x_1} &\ text {Multiplicar ambos lados por} x - x_1\\
m (x-x_1) & =( x-x_1)\ cdot\ dfrac {y-y_1} {x-x_1}\\
m (x-x_1) &=y-y_1&\ text {Por conveniencia, vamos a reescribir la ecuación.}\\
y-y_1&=m (x-x_1)
\ end {alineado}\)
Dado que esta ecuación se derivó usando un punto y la pendiente de una línea, se llama la forma punto-pendiente de una línea.
Si se nos da la pendiente,\(m\),\(y\) -interceptar\((0,b)\),, podemos sustituir esta información en la fórmula para pendiente.
\((0,b)\)Sea la\(y\) -intercepción y (x, y) sea cualquier otro punto de la línea. Entonces,
\ (\ begin {aligned}
m&=\ dfrac {y-b} {x-0}\\
m&=\ dfrac {y-b} {x} &\ text {Multiplica ambos lados por} x\
m\ cdot x&=\ not {x}\ cdot\ dfrac {y-b} {\ not {x}}\\
mx&=y-b&\ text {Resolver para} y\\
mx+b&=y&\ text {Para mayor comodidad, nosotros voy a reescribir esta ecuación}\\
y&=mx+b
\ end {alineado}\)
Dado que esta ecuación se derivó usando la pendiente y la intercepción, se llamó la forma pendiente-intercepción de una línea.
Resumimos estas dos derivaciones de la siguiente manera.
Formas de la Ecuación de una Línea
Podemos encontrar la ecuación de una línea si se nos da alguno de los siguientes conjuntos de información:
La pendiente,\(m\), y la\(y\) -intercepción\((0, b)\),, sustituyendo estos valores en:
\(y = mx + b\)
Esta es la forma pendiente-intercepción.
La pendiente\(m\), y cualquier punto\((x_1, y_1)\), sustituyendo estos valores en
\(y-y_1 = m(x-x_1)\)
Esta es la forma punto-pendiente.
Observe que ambas formas se basan en conocer la pendiente. Si nos dan dos puntos en la línea aún podemos encontrar la ecuación de la línea que pasa a través de ellos encontrando primero la pendiente de la línea, luego usando la forma de punto-pendiente.
Se acostumbra utilizar ya sea la forma pendiente-intercepción o la forma general para la forma final de la línea. Utilizaremos la forma pendiente-intercepción como forma final.
Conjunto de Muestras A
Encuentra la ecuación de la línea usando la información dada.
\(m = 6\),\(y\) -interceptar\((0, 4)\)
Ya que nos dan la pendiente y la\(y\) -intercepción, usaremos la forma pendiente-intercepción. \(m = 6, b = 4\).
\(y = mx + b\)
\(y = 6x + 4\)
\(m = -\dfrac{3}{4}\),\(y\) -interceptar\((0, \dfrac{1}{8})\)
Ya que nos dan la pendiente y la\(y\) -intercepción, usaremos la forma pendiente-intercepción. \(m = \dfrac{-3}{4}\),
\(b = \dfrac{1}{8}\)
\(y=mx + b\)
\(y = -\dfrac{3}{4}x + \dfrac{1}{8}\)
\(m = 2\), el punto\((4, 3)\).
Como se nos da la pendiente y algún punto, usaremos la forma punto-pendiente.
\(y - y_1 = m(x - x_1)\). Déjalo\((x_1, y_1)\) ser\((4,3)\).
\(y-3=2(x-4)\)Ponga esta ecuación en forma de pendiente-intercepción resolviendo para\(y\).
\(y-3=2x-8\)
\(y = 2x-5\)
\(m = -5\), el punto\((-3, 0)\)
Escribe la ecuación en forma de pendiente-intercepción.
Como se nos da la pendiente y algún punto, usaremos la forma punto-pendiente.
\ (\ begin {alineado}
y-y_1&=m (x-x_1) &\ text {Dejar} (x_1, y_1)\ texto {ser} (-3,0)\\
y-0&=-5 [x- (-3)]\
y&=-5 (x+3) &\ text {Resolver para} y\\
y&=-5x-15
\ end {alineado}\)
\(m = -1\), el punto\((0, 7)\).
Escribe la ecuación en forma de pendiente-intercepción.
Se nos da la pendiente y un punto, pero una observación cuidadosa revela que este punto es en realidad la\(y\) -intercepción. Así, usaremos la forma pendiente-intercepción. Si no hubiéramos visto este punto era la\(y\) -intercepción habríamos procedido con la forma punto-pendiente. Esto crearía un poco más de trabajo, pero aún así daría el mismo resultado.
Forma de Inclinación de Inclinación:
\ (\ begin {alineado}
y&=mx + b\\
y&= -1x + 7\\
y&= -x + 7
\ end {alineado}\)
Forma de punto-pendiente:
\ (\ begin {alineado}
y-y_1&=m (x-x_1)\\
y-7&=-1 (x-0)\\
y-7&=-x\
y&=-x+7
\ end {alineado}\)
Los dos puntos\((4, 1)\) y\((3, 5)\).
Escribe la ecuación en forma de pendiente-intercepción.
Ya que nos dan dos puntos, primero encontraremos la pendiente.
\(m = \dfrac{y_2-y_1}{x_2-x_1} = \dfrac{5-1}{3-4} = \dfrac{4}{-1} = -4\)
Ahora, tenemos la pendiente y dos puntos, podemos usar cualquiera de los puntos y la forma punto-pendiente.
Usando\((4, 1)\)
\ (\ begin {alineado}
y-y_1&=m (x-x_1)\\
y-1&=-4 (x-4)\\
y&=-4x+17
\ end {alineado}\)
Usando\((3, 5)\)
\ (\ begin {alineado}
y-y_1&=m (x-x_1)\\
y-5&=-4 (x-3)\\
y-5&=-4x + 12\\
y&=-4x+17
\ end {alineado}\)
Podemos ver que el uso de cualquiera da el mismo resultado.
Conjunto de práctica A
Encuentra la ecuación de cada línea dada la siguiente información. Utilice la forma pendiente-intercepción como la forma final de la ecuación.
\(m=5\),\(y\) -interceptar\((0,8)\).
- Contestar
-
\(y=5x+8\)
\(m=-8\),\(y\) -interceptar\((0,3)\).
- Contestar
-
\(y=−8x+3\)
\(m=2\),\(y\) -interceptar\((0,-7)\).
- Contestar
-
\(y=2x−7\)
\(m=1\),\(y\) -interceptar\((0,-1)\).
- Contestar
-
\(y=x−1\)
\(m=-1\),\(y\) -interceptar\((0,-10)\).
- Contestar
-
\(y=−x−10\)
\(m=4\), el punto\((5,2)\).
- Contestar
-
\(y=4x−18\)
\(m=-6\), el punto\((-1,0)\).
- Contestar
-
\(y=−6x−6\)
\(m=-1\), el punto\((-5,-5)\).
- Contestar
-
\(y=−x−10\)
Los dos puntos\((4, 1)\) y\((6, 5)\)
- Contestar
-
\(y=2x−7\)
Los dos puntos\((−7,−1)\) y\((−4,8)\).
- Contestar
-
\(y=3x+20\)
Conjunto de Muestras B
Encuentra la ecuación de la línea que pasa por el punto\((4, -7)\) que tiene pendiente\(0\).
Se nos da la pendiente y algún punto, así que usaremos la forma punto-pendiente. Con\(m = 0\) y\(x_1, y_1)\) como\((4, -7)\), tenemos:
\ (\ begin {alineado}
y-y_1 &= m (x-x_1)\\
y- (-7) &=0 (x-4)\\
y+7&=0\\
y&=-7
\ end {alineado}\)
Esta es una línea horizontal
Encuentra la ecuación de la línea que pasa por el punto\((1,3)\) dado que la línea es vertical.
Dado que la línea es vertical, la pendiente no existe. Por lo tanto, no podemos usar ni la forma pendiente-intercepción ni la forma punto-pendiente. Debemos recordar lo que sabemos de las líneas verticales. La ecuación de esta línea es simplemente\(x=1\).
Set de práctica B
Encuentra la ecuación de la línea que pasa por el punto\((2, 9)\) que tiene pendiente\(0\).
- Contestar
-
\(y=9\)
Encuentra la ecuación de la línea que pasa por el punto\((−1,6)\) dado que la línea es vertical.
- Contestar
-
\(x=−1\)
Conjunto de Muestras C
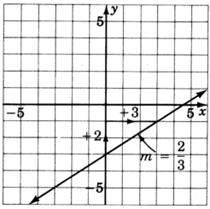
Al leer solo de la gráfica, determinar la ecuación de la línea.
La pendiente de la línea es\(\dfrac{2}{3}\), y la línea cruza el\(y\) eje -en el punto\((0, -3)\). Usando el formulario pendiente-intercepción obtenemos:
\(y = \dfrac{2}{3}x - 3\)
Set de práctica C
Al leer solo de la gráfica, determinar la ecuación de la línea.
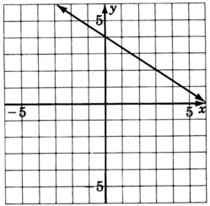
- Contestar
-
\(y = \dfrac{-2}{3}x + 4\)
Ejercicios
Para los siguientes problemas, escriba la ecuación de la línea usando la información dada en forma de pendiente-intercepción.
\(m=3\),\(y\) -interceptar\((0,4)\)
- Contestar
-
\(y=3x+4\)
\(m=2\),\(y\) -interceptar\((0,5)\)
\(m=8\),\(y\) -interceptar\((0,1)\)
- Contestar
-
\(y=8x+1\)
\(m=5\),\(y\) -interceptar\((0,-3)\)
\(m=-6\),\(y\) -interceptar\((0,-1)\)
- Contestar
-
\(y=−6x−1\)
\(m=-4\),\(y\) -interceptar\((0,0)\)
\(m=-\dfrac{3}{2}\),\(y\) -interceptar\((0,0)\)
- Contestar
-
\(y = -\dfrac{3}{2}x\)
\(m=3, (1,4)\)
\(m=1, (3,8)\)
- Contestar
-
\(y=x+5\)
\(m=2, (1,4)\)
\(m=8, (4,0)\)
- Contestar
-
\(y=8x−32\)
\(m=−3, (3,0)\)
\(m=−1, (6,0)\)
- Contestar
-
\(y=−x+6\)
\(m=−6, (0,0)\)
\(m=−2, (0,1)\)
- Contestar
-
\(y=−2x+1\)
\((0,0), (3,2)\)
\((0,0), (5,8)\)
- Contestar
-
\(y = \dfrac{8}{5}x\)
\((4,1), (6,3)\)
\((2,5), (1,4)\)
- Contestar
-
\(y=x+3\)
\((5,−3), (6,2)\)
\((2,3), (5,3)\)
- Contestar
-
\(y=3\)(línea horizontal)
\((−1,5), (4,5)\)
\((4,1), (4,2)\)
- Contestar
-
\(x=4\)(línea vertical)
\((2,7), (2,8)\)
\((3,3), (5,5)\)
- Contestar
-
\(y=x\)
\((0,0), (1,1)\)
\((−2,4), (3,−5)\)
- Contestar
-
\(y = -\dfrac{9}{5}x + \dfrac{2}{5}\)
\((1,6), (−1,−6)\)
\((14,12), (−9,−11)\)
- Contestar
-
\(y=x−2\)
\((0,−4), (5,0)\)
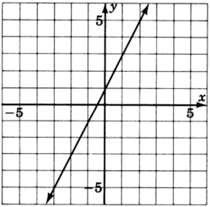
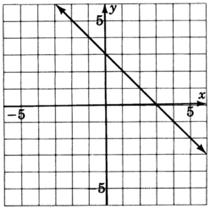
Para los siguientes problemas, lea solo de la gráfica y determine la ecuación de las líneas.
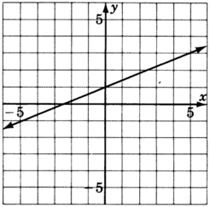
- Contestar
-
\(y = \dfrac{2}{5}x + 1\)
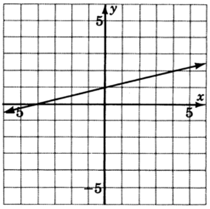
- Contestar
-
\(y = \dfrac{1}{4}x + 1\)
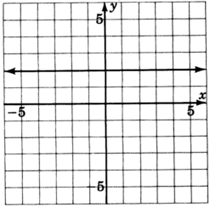
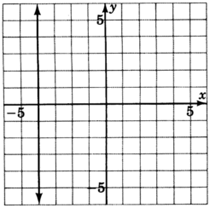
- Contestar
-
\(x=−4\)
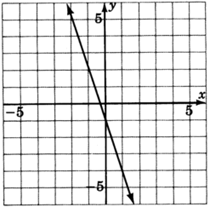
- Contestar
-
\(y=−3x−1\)
Ejercicios para la revisión
Graficar la ecuación\(x-3 = 0\)

Suministrar la palabra faltante. El punto en el que una línea cruza el\(y\) eje -se llama ____
- Contestar
-
\(y\)-interceptar
Suministrar la palabra faltante. El ____ de una línea es una medida de la inclinación de la línea.
Encuentra la pendiente de la línea que pasa por los puntos\((4,0)\) y\((−2,−6)\).
- Contestar
-
\(m=1\)
Graficar la ecuación\(3y = 2x + 3\)