8.6: Sumando y restando expresiones racionales
- Page ID
- 112143
Regla básica
Ahora estamos en condiciones de estudiar el proceso de sumar y restar expresiones racionales. Existe una regla de lo más básica a la que debemos adherirnos estrictamente si queremos sumar o restar convenientemente expresiones racionales.
Para sumar o restar convenientemente expresiones racionales, deben tener los mismos denominadores.
Así, para sumar o restar convenientemente dos o más expresiones racionales, debemos asegurarnos de que todas tengan el mismo denominador. El denominador que es más conveniente es el LCD.
Fracciones con el mismo denominador
Para sumar (o restar) dos o más expresiones racionales con los mismos denominadores, sumar (o restar) los numeradores y colocar el resultado sobre la LCD. Reducir si es necesario. Simbólicamente,
\(\dfrac{a}{c} + \dfrac{b}{c} = \dfrac{a+b}{c}\)
\(\dfrac{a}{c} - \dfrac{b}{c} = \dfrac{a-b}{c}\)
Tenga en cuenta que combinamos solo los numeradores.
Conjunto de Muestras A
Sumar o restar las siguientes expresiones racionales.
\ (\ begin {array} {vaciado a la izquierda}
\ dfrac {1} {6} +\ dfrac {3} {6} &&\ text {Los denominadores son los mismos. Añadir los numeradores.} \\
\ dfrac {1} {6} +\ dfrac {3} {6} &=\ dfrac {1+3} {6} =\ dfrac {4} {6} &\ text {Reducir}\
\ dfrac {1} {6} +\ dfrac {3} {6} &=\ dfrac {2} {3}
\ end {array}\)
\ (\ begin {array} {vaciado a la izquierda}
\ dfrac {5} {x} +\ dfrac {8} {x} &\ text {Los denominadores son los mismos. Añadir los numeradores}\\
\ dfrac {5} {x} +\ dfrac {5+8} {x} =\ dfrac {13} {x}
\ end {array}\)
\ (\ begin {array} {vaciado a la izquierda}
\ dfrac {2ab} {y^2w} -\ dfrac {5b} {y^2w} &\ text {Los denominadores son los mismos. Restar los numeradores}\\
\ dfrac {2ab} {y^2w} -\ dfrac {5b} {y^2w} =\ dfrac {2ab - 5b} {y^2w}
\ end {array}\)
\ (\ begin {array} {vaciado a la izquierda}
\ dfrac {3x^2 + x + 2} {x-7} +\ dfrac {x^2 - 4x + 1} {x-7} &\ text {Los denominadores son los mismos. Añadir los numeradores}\\
\ dfrac {3x^2 + x + 2} {x-7} +\ dfrac {x^2 - 4x + 1} {x-7} &=\ dfrac {3x^2 + x + 2 + x^2 - 4x + 1} {x-7}\\
&=\ dfrac {4x^2 - 3x + 3} {x-7}
\ end {array}\)
\ (\ begin {array} {vaciado a la izquierda}
\ dfrac {5y + 3} {2y - 5} -\ dfrac {2y + 4} {2y - 5} &&\ text {Los denominadores son los mismos. Restar los numeradores.}\\
&&\ text {Pero ten cuidado de restar todo el numerador. ¡Usa paréntesis!} \\
\ dfrac {5y + 3} {2y - 5} -\ dfrac {2y + 4} {2y - 5} &=\ dfrac {5y + 3 - (2y + 4)} {2y - 5}\\
& =\ dfrac {5y + 3 - 2y - 4} {2y - 5}\\
& =\ dfrac {3y - 1} {2y - 5}
\ end {array}\)
\(\text{ Note: } \dfrac{5y + 3}{2y - 5} - \dfrac{2y + 4}{2y - 5}\)
\(\text{ The term } -\dfrac{2y + 4}{2y - 5} \text{ could be written as}\)
\(+\dfrac{-(2y + 4)}{2y - 5} = \dfrac{-2y - 4}{2y - 5}\)
Un error común es escribir:
\(-\dfrac{2y + 4}{2y - 5}\)como\(\dfrac{-2y + 4}{2y - 5}\)
Esto no es correcto, ya que el signo negativo no se está aplicando a todo el numerador
\(\dfrac{3x^2 + 4x + 5}{(x+6)(x-2)} + \dfrac{2x^2 + x + 6}{x^2 + 4x - 12} - \dfrac{x^2 - 4x - 6}{x^2 + 4x - 12}\)
Facturar los denominadores para determinar si son los mismos:
\(\dfrac{3x^2 + 4x + 5}{(x+6)(x-2)} + \dfrac{2x^2 + x + 6}{(x+6)(x-2)} - \dfrac{x^2 - 4x - 6}{(x+6)(x-2)}\)
Los denominadores son los mismos. Combina los numeradores teniendo cuidado de anotar el signo negativo.
\(\dfrac{3x^2 + 4x + 5 + 2x^2 + x + 6 - (x^2 - 4x + 6)}{(x+6)(x-2)}\)
\(\dfrac{3x^2 + 4x + 5 + 2x^2 + x + 6 - x^2 + 4x + 6}{(x+6)(x-2)}\)
\(\dfrac{4x^2 + 9x + 17}{(x+6)(x-2)}\)
Conjunto de práctica A
Sumar o restar las siguientes expresiones racionales.
\(\dfrac{4}{9} + \dfrac{2}{9}\)
- Contestar
-
\(\dfrac{2}{3}\)
\(\dfrac{3}{b} + \dfrac{2}{b}\)
- Contestar
-
\(\dfrac{5}{b}\)
\(\dfrac{5x}{2y^2} - \dfrac{3x}{2y^2}\)
- Contestar
-
\(\dfrac{x}{y^2}\)
\(\dfrac{x+y}{x-y} + \dfrac{2x + 3y}{x - y}\)
- Contestar
-
\(\dfrac{3x + 4y}{x - y}\)
\(\dfrac{4x^2 - x + 4}{3x + 10} - \dfrac{x^2 + 2x + 5}{3x + 10}\)
- Contestar
-
\(\dfrac{3x^2 - 3x - 1}{3x + 10}\)
\(\dfrac{x(x+1)}{x(2x + 3)} + \dfrac{3x^2 - x + 7}{2x^2 + 3x}\)
- Contestar
-
\(\dfrac{4x^2 + 7}{x(2x + 3)}\)
\(\dfrac{4x + 3}{x^2 - x - 6} - \dfrac{8x - 4}{(x+2)(x-3)}\)
- Contestar
-
\(\dfrac{-4x + 7}{(x+2)(x - 3)}\)
\(\dfrac{5a^2 + a - 4}{2a(a - 6)} + \dfrac{2a^2 + 3a + 4}{2a^2 - 12a} + \dfrac{a^2 + 2}{2a^2 - 12a}\)
- Contestar
-
\(\dfrac{4a^2 + 2a + 1}{a(a-6)}\)
\(\dfrac{8x^2 + x - 1}{x^2 - 6x + 8} + \dfrac{2x^2 + 3x}{x^2 - 6x + 8} - \dfrac{5x^2 + 3x - 4}{(x-4)(x-2)}\)
- Contestar
-
\(\dfrac{5x^2 + x + 3}{(x-4)(x-2)}\)
Fracciones con diferentes denominadores
Conjunto de Muestras B
Sumar o restar las siguientes expresiones racionales.
\ (\ begin {array} {vaciado a la izquierda}
\ dfrac {4a} {3y} +\ dfrac {2a} {8y^2}. &\ text {Los denominadores no son los mismos. Encuentra la pantalla LCD. Por inspección, el LCD es} 9y^2\\
&\ text {El denominador de la primera expresión racional se ha multiplicado por} 3y\\
\ dfrac {?} {9y^2} +\ dfrac {2a} {9y^2} &\ text {así se debe multiplicar el numerador por} 3y\\
4a\ cdot 3y = 12ay\
\ dfrac {12ay} {9y^2} +\ dfrac {2a} {9y^2} &\ text {Los denominadores son ahora los mismos. Añadir los numeradores.} \\
\ dfrac {12ay + 2a} {9y^2}
\ end {array}\)
\ (\ begin {array} {vaciado a la izquierda}
\ dfrac {3b} {b + 2} +\ dfrac {5b} {b-3} &\ text {Los denominadores no son los mismos. El LCD es} (b + 2) (b-3)\\
\ dfrac {?} {(b+2) (b-3)} +\ dfrac {?} {(b+2) (b-3)} &\ text {El denominador de la primera expresión racional se ha multiplicado por} b-3,\\
&\ text {así que el numerador debe multiplicarse por} b-3. \\
3b (b-3)\\
\ dfrac {3b (b-3)} {(b+2) (b-3)} +\ dfrac {?} {(b+2) (b-3)} &\ text {El denominador de la segunda expresión racional se ha multiplicado por} b + 2,\\
&\ text {por lo que el numerador debe multiplicarse por} b + 2. \\
5b (b + 2). \\
\ dfrac {3b (b-3)} {(b+2) (b-3)} +\ dfrac {5b (b+2)} {(b+2) (b-3)} &\ text {Los denominadores son ahora los mismos. Añadir los numeradores.}
\ end {array}\)
\ (\ begin {array} {vaciado a la izquierda}
\ dfrac {3b (b-3) + 5b (b + 2)} {(b-3) (b+2)} &=\ dfrac {3b^2 - 9b + 5b^2 + 10b} {(b-3) (b+2)}
& =\ dfrac {8b^2 + b} {(b-3) (b+2)}
\ end {array}\)
\ (\ begin {array} {vaciado a la izquierda}
\ dfrac {x+3} {x-1} +\ dfrac {x-2} {4x + 4} &\ text {Los denominadores no son iguales}\\
&\ text {Encuentra la pantalla LCD}
\\ dfrac {x + 3} {x-1} +\ dfrac {x - 2} {4 (x+1)} &\ texto {El LCD es} (x + 1) (x - 1)\\
\ dfrac {?} {4 (x+1) (x-1)} +\ dfrac {?} {4 (x+1) (x-1)} &\ text {El denominador de la primera expresión racional se ha multiplicado por} 4 (x+1)\\
&\ text {el numerador debe multiplicarse por} 4 (x+1)\\
4 (x + 3) (x+1)
\\ dfrac {4 (x+3) (x+1)} {4 (x+1) (x-1)} +\ frac {?} {4 (x+1) (x-1)} &\ text {El denominador de la segunda expresión racional se ha multiplicado por} (x-1)\\
&\ text {así el numerador debe multiplicarse por} x-1\\
(x-1) (x-2)
\\ dfrac {4 (x+3) (x+1)} {4 (x+1) (x-1)} +\ dfrac {(-1) (x-2)} {4 (x+1) (x-2)} &\ text {El denominador ahora son los mismos.} \\
&\ text {Agrega los numeradores}\\
\ dfrac {4 (x+3) (x+1) + (x-1) (x-2)} {4 (x+1) (x-1)}\
\ dfrac {4 (x^2 + 4x + 3) + x^2 - 3x + 2} {4 (x + 1) (x-1)}
\ end {array}\)
\(\dfrac{4x^2 + 16x + 12 + x^2 - 3x + 2}{4(x+1)(x-1)} = \dfrac{5x^2 + 13x + 14}{4(x+1)(x-1)}\)
\ (\ begin {array} {vaciado a la izquierda}
\ dfrac {x+5} {x^2 - 7x + 12} +\ dfrac {3x - 1} {x^2 - 2x - 3} &\ text {Determina la pantalla LCD}\\
\ dfrac {x+5} {(x-4) (x-3)} +\ dfrac {3x - 1} {(x-3) (x+1) (x+1))} &\ text {El LCD es} (x-4) (x-3) (x+1)\
\\ dfrac {?} {(x-4) (x-3) (x+1)} +\ dfrac {?} {(x-4) (x-3) (x+1)} &\ text {El primer numerador debe ser multiplicado por} x + 1\ texto {y el segundo por} x-4\\
\ dfrac {(x+5) (x+1)} {(x-4) (x-3) (x+1)} +\ dfrac {(3x - 1) (x - 4)} {(x-4) (x-3) (x+1)} &\ text {Los denominadores son ahora los mismos. Agregar los numeradores}\\
\ dfrac {(x+5) (x+1) + (3x-1) (x-4)} {(x-4) (x-3) (x+1)}\
\ dfrac {x^2 + 6x + 5 = 3x^2 + -13x + 4} {(x-4) (x-3) (x+1)}\
\ dfrac {4x^2 - 7x + 9} {(x-4) (x-3) (x+1)}
\ end {array}\)
\ (\ begin {array} {vaciado a la izquierda}
\ dfrac {a+4} {a^2 + 5a + 6} -\ dfrac {a-4} {a^2 - 5a - 24} &\ text {Determinar la pantalla LCD}
\\\ dfrac {a+4} {(a+3) (a+3) (a+2)} -\ dfrac {a-4} {(a+3)} &\ text {El LCD es} (a+3) (a+2) (a-8)\\
\ dfrac {?} {(a+3) (a+2) (a-8)} -\ dfrac {?} {(a+3) (a+2) (a-8)} &\ text {El primer numerador debe ser multiplicado por} a-8\ text {y el segundo por} a+2. \
\ dfrac {(a+4) (a-8)} {(a+3) (a+2) (a-8)} -\ dfrac {(a-4) (a+2)} {(a+3) (a+2) (a-8)} &\ text {Los denominadores son ahora los mismos. Restar los numeradores.} \\
\ dfrac {(a+4) (a-8) - (a-4) (a+2)} {(a+3) (a+2) (a-8)}\
\ dfrac {a^2 - 4a - 32 - (a^2 - 2a - 8)} {(a+3) (a+2) (a-8)}\
\ dfrac {a^2 - 4a - 32 - a^^2 + 2a + 8} {(a+3) (a+2) (a-8)}\
\\ dfrac {-2a-24} {(a+3) (a+2) (a-8)} &\ text {Factor} -2\ texto {del numerador.} \
\ dfrac {-2 (a+12)} {(a+3) (a+2) (a-8)}
\ end {array}\)
\ (\ begin {array} {vaciado a la izquierda}
\ dfrac {3x} {7-x} +\ dfrac {5x} {x-7} &&\ text {Los denominadores son casi los mismos. Se diferencian solo en signo}\\
&&\ text {Nuestra técnica es factorial} -1\ text {de uno de ellos}\
\\ dfrac {3x} {7-x} =\ dfrac {3x} {- (x-7)} &=\ dfrac {-3x} {x-7}\
\ dfrac {3x} {7-x} +\ dfrac {5x} {x-7} &=\ dfrac {-3x} {x-7} +\ dfrac {5x} {x-7}\\
&=\ dfrac {-3x + 5x} {x-7}\\
&=\ dfrac {2x} {x-7}
\ end {array}\)
Set de práctica B
Sumar o restar las siguientes expresiones racionales.
\(\dfrac{3x}{4a^2} + \dfrac{5x}{12a^3}\)
- Contestar
-
\(\dfrac{9ax + 5x}{12a^3}\)
\(\dfrac{5b}{b+1} + \dfrac{3b}{b-2}\)
- Contestar
-
\(\dfrac{8b^2 - 7b}{(b+1)(b-2)}\)
\(\dfrac{a-7}{a+2} + \dfrac{a-2}{a+3}\)
- Contestar
-
\(\dfrac{2a^2 - 4a - 25}{(a+2)(a+3)}\)
\(\dfrac{4x + 1}{x+3} - \dfrac{x+5}{x-3}\)
- Contestar
-
\(\dfrac{3x^2 - 19x - 18}{(x+3)(x-3)}\)
\(\dfrac{2y-3}{y} + \dfrac{3y + 1}{y + 4}\)
- Contestar
-
\(\dfrac{5y^2 + 6y - 12}{y(y + 4)}\)
\(\dfrac{a-7}{a^2 - 3a + 2} + \dfrac{a + 2}{a^2 - 6a + 8}\)
- Contestar
-
\(\dfrac{2a^2 - 10a + 26}{(a-2)(a-1)(a-4)}\)
\(\dfrac{6}{b^2 + 6b + 9} - \dfrac{2}{b^2 + 4b + 4}\)
- Contestar
-
\(\dfrac{4b^2 + 12b + 6}{(b+3)^2(b+2)^2}\)
\(\dfrac{x}{x+4} - \dfrac{x-2}{3x-3}\)
- Contestar
-
\(\dfrac{2x^2 - 5x + 8}{3(x+4)(x-2)}\)
\(\dfrac{5x}{4-x} + \dfrac{7x}{x-4}\)
- Contestar
-
\(\dfrac{2x}{x-4}\)
Conjunto de Muestras C
Combina las siguientes expresiones racionales.
\ (\ begin {array} {vaciado izquierdo}
3 +\ dfrac {7} {x-1} &\ text {Reescribe la expresión}\\
\ dfrac {3} {1} +\ dfrac {7} {x-1} &\ text {La pantalla es} x-1\
\ dfrac {3 (x-1)} {x-1} +\ dfrac {7} {x-1} +\ dfrac {7} {-1} =\ dfrac {3x-3} {x-1} +\ dfrac {7} {x-1} &=\ dfrac {3x-3+7} {x-1}\\
&= \ dfrac {3x + 4} {x-1}
\ end {array}\)
\ (\ begin {array} {vaciado a la izquierda}
3y + 4 -\ dfrac {y^2 - y +3} {y-6} &\ text {Reescribe la expresión.} \\
\ dfrac {3y + 4} {1} -\ dfrac {y^2 - y + 3} {y - 6} &\ text {La pantalla es} y-6\
\ dfrac {(3y+4) (y-6)} {y-6} -\ dfrac {y^-y+3} {y-6} &=\ dfrac {(3y+4) (y-6) - (y^2 - y +3)} {y-6}\\
&=\ dfrac {3y^2 - 14y - 24 - y^2 + y - 3} {y-6}\\
&=\ dfrac {2y^2 - 13y - 27} {y-6}
\ end {array}\)
Set de práctica C
Simplificar\(8 + \dfrac{3}{x-6}\)
- Contestar
-
\(\dfrac{8x - 45}{x-6}\)
Simplificar\(2a - 5 - \dfrac{a^2 + 2a - 1}{a+3}\)
- Contestar
-
\(\dfrac{a^2 - a - 14}{a + 3}\)
Ejercicios
Para los siguientes problemas, sumar o restar las expresiones racionales.
\(\dfrac{3}{8} + \dfrac{1}{8}\)
- Contestar
-
\(\dfrac{1}{2}\)
\(\dfrac{1}{9} + \dfrac{4}{9}\)
\(\dfrac{7}{10} - \dfrac{2}{5}\)
- Contestar
-
\(\dfrac{3}{10}\)
\(\dfrac{3}{4} - \dfrac{5}{12}\)
\(\dfrac{3}{4x} + \dfrac{5}{4x}\)
- Contestar
-
\(\dfrac{2}{x}\)
\(\dfrac{2}{7y} + \dfrac{3}{7y}\)
\(\dfrac{6y}{5x} + \dfrac{8y}{5x}\)
- Contestar
-
\(\dfrac{14y}{5x}\)
\(\dfrac{9a}{7b} + \dfrac{3a}{7b}\)
\(\dfrac{15n}{2m} - \dfrac{6n}{2m}\)
- Contestar
-
\(\dfrac{9n}{2m}\)
\(\dfrac{8p}{11q} - \dfrac{3p}{11q}\)
\(\dfrac{y+4}{y-6} + \dfrac{y+8}{y-6}\)
- Contestar
-
\(\dfrac{2y + 12}{y - 6}\)
\(\dfrac{y-1}{y+4} + \dfrac{y+7}{y+4}\)
\(\dfrac{a+6}{a-1} + \dfrac{3a+5}{a-1}\)
- Contestar
-
\(\dfrac{4a + 11}{a - 1}\)
\(\dfrac{5a + 1}{a+7} + \dfrac{2a - 6}{a + 7}\)
\(\dfrac{x + 1}{5x} + \dfrac{x + 3}{5x}\)
- Contestar
-
\(\dfrac{2x + 4}{5x}\)
\(\dfrac{a - 6}{a + 2} + \dfrac{a - 2}{a+2}\)
\(\dfrac{b + 1}{b - 3} + \dfrac{b + 2}{b - 3}\)
- Contestar
-
\(\dfrac{2b + 3}{b-3}\)
\(\dfrac{a + 2}{a - 5} - \dfrac{a+3}{a-5}\)
\(\dfrac{b + 7}{b-6} - \dfrac{b-1}{b-6}\)
- Contestar
-
\(\dfrac{8}{b-6}\)
\(\dfrac{2b + 3}{b+1} - \dfrac{b-4}{b+1}\)
\(\dfrac{3y + 4}{y + 8} - \dfrac{2y - 5}{y + 8}\)
- Contestar
-
\(\dfrac{y + 9}{y + 8}\)
\(\dfrac{2a - 7}{a - 9} + \dfrac{3a + 5}{a - 9}\)
\(\dfrac{8x - 1}{x + 2} - \dfrac{15x + 7}{x + 2}\)
- Contestar
-
\(\dfrac{-7x - 8}{x + 2}\)
\(\dfrac{7}{2x^2} + \dfrac{1}{6x^3}\)
\(\dfrac{2}{3x} + \dfrac{4}{6x^2}\)
- Contestar
-
\(\dfrac{2(x+1)}{3x^2}\)
\(\dfrac{5}{6y^3} - \dfrac{2}{18y^5}\)
\(\dfrac{2}{5a^2} - \dfrac{1}{10a^3}\)
- Contestar
-
\(\dfrac{4a - 1}{10a^3}\)
\(\dfrac{3}{x+1} + \dfrac{5}{x-2}\)
\(\dfrac{4}{x-6} + \dfrac{1}{x-1}\)
- Contestar
-
\(\dfrac{5(x-2)}{(x-6)(x-1)}\)
\(\dfrac{2a}{a+1} - \dfrac{3a}{a+4}\)
\(\dfrac{6y}{y + 4} + \dfrac{2y}{y + 3}\)
- Contestar
-
\(\dfrac{2y(4y + 13)}{(y+4)(y+3)}\)
\(\dfrac{x-1}{x-3} + \dfrac{x + 4}{x-4}\)
\(\dfrac{x+2}{x-5} + \dfrac{x-1}{x+2}\)
- Contestar
-
\(\dfrac{2x^2 - 2x + 9}{(x-5)(x+2)}\)
\(\dfrac{a+3}{a-3} - \dfrac{a+2}{a-2}\)
\(\dfrac{y+1}{y-1} - \dfrac{y+4}{y-4}\)
- Contestar
-
\(\dfrac{-6y}{(y-1)(y-4)}\)
\(\dfrac{x-1}{(x+2)(x-3)} + \dfrac{x+4}{x-3}\)
\(\dfrac{y+2}{(y+1)(y+6)} + \dfrac{y-2}{y+6}\)
- Contestar
-
\(\dfrac{y^2}{(y+1)(y+6)}\)
\(\dfrac{2a + 1}{(a+3)(a-3)} - \dfrac{a+2}{a+3}\)
\(\dfrac{3a + 5}{(a+4)(a-1)} - \dfrac{2a - 1}{a - 1}\)
- Contestar
-
\(\dfrac{-2a^2 - 4a + 9}{(a+4)(a-1)}\)
\(\dfrac{2x}{x^2 - 3x + 2} + \dfrac{3}{x-2}\)
\(\dfrac{4a}{a^2 - 2a - 3} + \dfrac{3}{a + 1}\)
- Contestar
-
\(\dfrac{7a - 9}{(a+1)(a-3)}\)
\(\dfrac{3y}{y^2 - 7y + 12} - \dfrac{y^2}{y-3}\)
\(\dfrac{x-1}{x^2 + 6x + 8} + \dfrac{x+3}{x^2 + 2x - 8}\)
- Contestar
-
\(\dfrac{2(x^2 + x + 4)}{(x+2)(x-2)(x+4)}\)
\(\dfrac{a-4}{a^2 + 2a - 3} + \dfrac{a+2}{a^2 + 3a - 4}\)
\(\dfrac{x-1}{x^2 + 6x + 8} + \dfrac{x + 3}{x^2 + 2x - 8}\)
- Contestar
-
\(\dfrac{2(x^2 + x + 4)}{(x+2)(x-2)(x+4)}\)
\(\dfrac{a-4}{a^2 + 2a - 3} + \dfrac{a + 2}{a^2 + 3a - 4}\)
\(\dfrac{b-3}{b^2 + 9b + 20} + \dfrac{b+4}{b^2 + b - 12}\)
- Contestar
-
\(\dfrac{2b^2 + 3b + 29}{(b-3)(b+4)(b+5)}\)
\(\dfrac{y-1}{y^2 + 4y - 12} - \dfrac{y + 3}{y^2 + 6y - 16}\)
\(\dfrac{x+3}{x^2 + 9x + 13} - \dfrac{x - 5}{x^2 - 4}\)
- Contestar
-
\(\dfrac{-x + 29}{(x-2)(x+2)(x+7)}\)
\(\dfrac{x-1}{x^2 - 4x + 3} + \dfrac{x + 3}{x^2 - 5x + 6} + \dfrac{2x}{x^2 - 3x + 2}\)
\(\dfrac{4x}{x^2 + 6x + 8} + \dfrac{3}{x^2 + x - 6} + \dfrac{x-1}{x^2 + x - 12}\)
- Contestar
-
\(\dfrac{5x^4 - 3x^3 - 34x^2 + 34x - 60}{(x-2)(x+2)(x-3)(x+3)(x+4)}\)
\(\dfrac{y + 2}{y^2 - 1} + \dfrac{y-3}{y^2 - 3y - 4} - \dfrac{y + 3}{y^2 - 5y + 4}\)
\(\dfrac{a - 2}{a^2 - 9a + 18} + \dfrac{a - 2}{a^2 - 4a - 12} - \dfrac{a - 2}{a^2 - a - 6}\)
- Contestar
-
\(\dfrac{(a+5)(a-2)}{(a+2)(a-3)(a-6)}\)
\(\dfrac{y-2}{y^2 + 6y} + \dfrac{y + 4}{y^2 + 5y - 6}\)
\(\dfrac{a + 1}{a^3 + 3a^2} - \dfrac{a + 6}{a^2 - a}\)
- Contestar
-
\(\dfrac{-a^3 - 8a^2 - 18a - 1}{a^2(a+3)(a-1)}\)
\(\dfrac{4}{3b^2 - 12b} - \dfrac{2}{6b^2 - 6b}\)
\(\dfrac{3}{2x^5 - 4x^4} + \dfrac{-2}{8x^3 + 24x^2}\)
- Contestar
-
\(\dfrac{-x^3 + 2x^2 + 6x + 18}{4x^4(x-2)(x+3)}\)
\(\dfrac{x + 2}{12x^3} + \dfrac{x + 1}{4x^2 + 8x - 12} - \dfrac{x + 3}{16x^2 - 32x + 16}\)
\(\dfrac{2x}{x^2 - 9} - \dfrac{x + 1}{4x^2 - 12x} - \dfrac{x-4}{8x^3}\)
- Contestar
-
\(\dfrac{14x^4 - 9x^3 - 2x^2 + 9x - 36}{8x^3(x + 3)(x - 3)}\)
\(4 + \dfrac{3}{x+2}\)
\(8 + \dfrac{2}{x+6}\)
- Contestar
-
\(\dfrac{8x + 50}{x + 6}\)
\(1 + \dfrac{4}{x-7}\)
\(3 + \dfrac{5}{x-6}\)
- Contestar
-
\(\dfrac{3x - 13}{x - 6}\)
\(-2 + \dfrac{4x}{x+5}\)
\(-1 + \dfrac{3a}{a-1}\)
- Contestar
-
\(\dfrac{2a + 1}{a - 1}\)
\(6 - \dfrac{4y}{y + 2}\)
\(2x + \dfrac{x^2 - 4}{x + 1}\)
- Contestar
-
\(\dfrac{3x^2 + 2x - 4}{x + 1}\)
\(-3y + \dfrac{4y^2 + 2y - 5}{y + 3}\)
\(x + 2 + \dfrac{x^2 + 4}{x-1}\)
- Contestar
-
\(\dfrac{2x^2 + x + 2}{x - 1}\)
\(b + 6 + \dfrac{2b + 5}{b-2}\)
\(\dfrac{3x - 1}{x - 4} - 8\)
- Contestar
-
\(\dfrac{-5x + 31}{x - 4}\)
\(\dfrac{4y + 5}{y + 1} - 9\)
\(\dfrac{2y^2 + 11y - 1}{y + 4} - 3y\)
- Contestar
-
\(\dfrac{-(y^2 + y + 1)}{y+4}\)
\(\dfrac{5y^2 - 2y + 1}{y^2 + y - 6} - 2\)
\(\dfrac{4a^3 + 2a^2 + a - 1}{a^2 + 11a + 28} + 3a\)
- Contestar
-
\(\dfrac{7a^3 + 35a^2 + 85a - 1}{(a+7)(a+4)}\)
\(\dfrac{2x}{1-x} + \dfrac{6x}{x-1}\)
\(\dfrac{5m}{6-m} + \dfrac{3m}{m-6}\)
- Contestar
-
\(\dfrac{-2m}{m-6}\)
\(\dfrac{-a+7}{8-3a} + \dfrac{2a + 1}{3a - 8}\)
Ejercicios para revisión
Simplificar\((x^3y^2z^5)^6(x^2yz)^2\)
- Contestar
-
\(x^{22}y^{14}z^{32}\)
Escribe\(6a^{-3}b^4c^{-2}a^{-1}b^{-5}c^3\) para que solo aparezcan exponentes positivos.
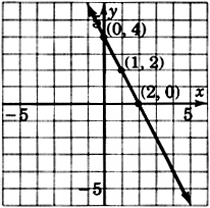
Construye la gráfica de\(y = -2x + 4\)
- Contestar
-
Encuentra el producto\(\dfrac{x^2 - 3x - 4}{x^2 + 6x + 5} \cdot \dfrac{x^2 + 5x + 6}{x^2 - 2x - 8}\)
Reemplazar \(N\)con la cantidad adecuada:\(\dfrac{x+3}{x-5} = \dfrac{N}{x^2 - 7x + 10}\)
- Contestar
-
\((x+3)(x−2)\)


