9.2: Expresiones de raíz cuadrada
- Page ID
- 112394
Raíces Cuadradas
Cuando estudiamos exponentes en la Sección 2.5, notamos que\(4^2 = 16\) y\((-4)^2 = 16\). Podemos ver que\(16\) es un cuadrado de ambos\(4\) y\(-4\). Ya que\(16\) proviene de la cuadratura\(4\) o\(-4\),\(4\) y\(-4\) se llaman las raíces cuadradas de\(16\). Así,\(16\) tiene dos raíces cuadradas,\(4\) y\(-4\). Observe que estas dos raíces cuadradas son opuestas entre sí.
Podemos decir que
La raíz cuadrada de un número positivo\(x\) es un número tal que cuando se cuadra el número\(x\) resulta.
Cada número positivo tiene dos raíces cuadradas, una raíz cuadrada positiva y una raíz cuadrada negativa. Además, las dos raíces cuadradas de un número positivo son opuestas entre sí. La raíz cuadrada de 0 es 0.
Conjunto de Muestras A
Las dos raíces cuadradas de\(49\) son\(7\) y\(-7\) desde:
\(7^2 = 49\)y\((-7)^2 = 49\).
Las dos raíces cuadradas de\(\dfrac{49}{64}\) son\(\dfrac{7}{8}\) y\(\dfrac{-7}{8}\) desde:
\((\dfrac{7}{8})^2 = \dfrac{7}{8} \cdot \dfrac{7}{8} = \dfrac{49}{64}\)y\((\dfrac{-7}{8})^2 = \dfrac{-7}{8} \cdot \dfrac{-7}{8} = \dfrac{49}{64}\)
Conjunto de práctica A
Nombra ambas raíces cuadradas de cada uno de los siguientes números.
\(36\)
- Contestar
-
\(6\)y\(-6\)
\(25\)
- Contestar
-
\(5\)y\(-5\).
\(100\)
- Contestar
-
\(10\)y\(-10\)
\(64\)
- Contestar
-
\(8\)y\(-8\)
\(1\)
- Contestar
-
\(1\)y\(-1\)
\(\dfrac{1}{4}\)
- Contestar
-
\(\dfrac{1}{2}\)y\(-\dfrac{1}{2}\)
\(\dfrac{9}{16}\)
- Contestar
-
\(\dfrac{3}{4}\)y\(-\dfrac{3}{4}\)
\(0.1\)
- Contestar
-
\(0.1\)y\(−0.1\)
\(0.09\)
- Contestar
-
\(0.03\)y\(−0.03\)
Raíz cuadrada principal y secundaria
Hay una notación para distinguir la raíz cuadrada positiva de un número\(x\) de la raíz cuadrada negativa de\(x\).
Si\(x\) es un número real positivo, entonces
\(\sqrt{x}\)representa la raíz cuadrada positiva de\(x\). La raíz cuadrada positiva de un número se llama la raíz cuadrada principal del número.
\(-\sqrt{x}\)representa la raíz cuadrada negativa de\(x\). La raíz cuadrada negativa de un número se llama raíz cuadrada secundaria del número.
\(-\sqrt{x}\)indica la raíz cuadrada secundaria de\(x\).
En la expresión\(\sqrt{x}\),
\(\sqrt{}\)se llama un signo radical.
\(x\)se llama el radicando.
\(\sqrt{x}\)se llama radical
La barra horizontal que aparece unida al signo radical,\(\sqrt{}\), es un símbolo de agrupación que especifica el radicando.
Porque\(\sqrt{x}\) y\(-\sqrt{x}\) son las dos raíces cuadradas de\(x\),
\((\sqrt{x})(\sqrt{x}) = x\)y\((-\sqrt{x})(-\sqrt{x}) = x\).
Conjunto de Muestras B
Escriba las raíces cuadradas principal y secundaria de cada número.
\(9\)
Raíz cuadrada principal:\(\sqrt{9} = 3\)
Raíz cuadrada secundaria:\(-\sqrt{9} = -3\)
\(15\)
Raíz cuadrada principal:\(\sqrt{15}\)
Raíz cuadrada secundaria:\(-\sqrt{15}\)
Utilice una calculadora para obtener una aproximación decimal para las dos raíces cuadradas de\(34\). Redondear a dos decimales.
En la calculadora:
Tipo:\(34\)
Prensa:\(\sqrt{}\)
La pantalla lee:\(5.8309519\)
Redondeo a\(5.83\)
Observe que el símbolo de raíz cuadrada en la calculadora es\(\sqrt{}\). Esto significa, por supuesto, que una calculadora producirá sólo la raíz cuadrada positiva. Debemos suministrar nosotros mismos la raíz cuadrada negativa.
\(\sqrt{34}\)\ aprox 5.83\) y\(-\sqrt{34} \approx -5.83\)
Aviso: el símbolo\(\approx\) significa “aproximadamente igual a”.
¿El número\(\sqrt{50}\) está entre qué dos números enteros?
Ya que\(7^2 = 49, \sqrt{49} = 7\).
Ya que\(8^2 = 64, \sqrt{64} = 8\). Así,
\(7 < \sqrt{50} < 8\)
Así,\(\sqrt{50}\) es un número entre\(7\) y\(8\).

Set de práctica B
Escriba las raíces cuadradas principal y secundaria de cada número.
\(100\)
- Contestar
-
\(\sqrt{100} = 10\)y\(-\sqrt{100} = -10\)
\(121\)
- Contestar
-
\(\sqrt{121} = 11\)y\(-\sqrt{121} = -11\)
\(35\)
- Contestar
-
\(\sqrt{35}\)y\(-\sqrt{35}\)
Utilice una calculadora para obtener una aproximación decimal para las dos raíces cuadradas de\(35\). Redondear a dos decimales.
- Contestar
-
\ 95.92\) y\(-5.92\)
Expresiones significativas
Ya que sabemos que el cuadrado de cualquier número real es un número positivo o cero, podemos ver que expresiones como\(\sqrt{-16}\) no describen números reales. No hay un número real que pueda ser cuadrado que produzca\(-16\). \(\sqrt{x}\)Para ser un número real, debemos tener\(x \ge 0\). En nuestro estudio del álgebra, asumiremos que todas las variables y todas las expresiones en los radicandos representan números no negativos (números mayores o iguales a cero).
Conjunto de Muestras C
Escribe las restricciones adecuadas que se deben colocar en la variable para que cada expresión represente un número real.
\(\sqrt{x-3}\)para ser un número real, debemos tener:
\(x - 3 \ge 0\)o\(x \ge 3\)
\(\sqrt{2m + 7}\)Para ser un número real, debemos tener:
\(2m + 7 \ge 0\)\(2m \ge -7\)o\(m \ge \dfrac{-7}{2}\)
Set de práctica C
Escribe las restricciones adecuadas que se deben colocar en la variable para que cada expresión represente un número real.
\(\sqrt{x+5}\)
- Contestar
-
\(x \ge -5\)
\(\sqrt{y - 8}\)
- Contestar
-
\(y≥8\)
\(\sqrt{3a + 2}\)
- Contestar
-
\(a \ge -\dfrac{2}{3}\)
\(\sqrt{5m - 6}\)
- Contestar
-
\(m \ge \dfrac{6}{5}\)
Simplificando las raíces cuadradas
Cuando las variables ocurren en el radicando, muchas veces podemos simplificar la expresión eliminando el signo radical. Podemos hacerlo teniendo presente que el radicando es el cuadrado de alguna otra expresión. Podemos simplificar a un radical buscando una expresión cuyo cuadrado es el radicando. Las siguientes observaciones nos ayudarán a encontrar la raíz cuadrada de una cantidad variable.
Ya que\((x^3)^2 = x^{3 \cdot 2} - x^6, x^3\) es una raíz cuadrada de\(x^6\). También
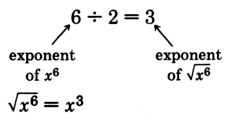
Ya que\((x^4)^2 = x^{4 \cdot 2} = x^8, x^4\) es una raíz cuadrada de\(x^8\). También
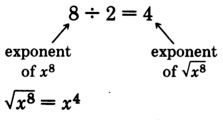
Ya que\((x^6)^2 = x^{6 \cdot 2} = x^{12}, x^6\) es una raíz cuadrada de\(x^{12}\). También
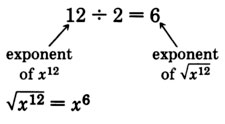
Estos ejemplos sugieren la siguiente regla:
Si una variable tiene un exponente par, su raíz cuadrada se puede encontrar dividiendo ese exponente por\(2\).
Los ejemplos del Conjunto de Muestras B ilustran el uso de esta regla.
Conjunto de Muestras D
Simplifica cada expresión eliminando el signo radical. Supongamos que cada variable es no negativa.
\(\sqrt{a^2}\)Buscamos una expresividad cuya plaza es\(a^2\). Dado que\((a)^2 = a^2\),
\(\sqrt{a^2} = a\)Observe que\(2 \div 2 = 1\)
\(\sqrt{y^8}\)Buscamos una expresión cuya plaza es\(y^8\). Dado que\((y^4)^2 = y^8\),
\(\sqrt{y^8} = y^4\)Observe eso\(8 \div 2 = 4\).
\(\sqrt{25m^2n^6}\). Buscamos una expresión cuya plaza es\(25m^2n^6\). Dado que\((5mn^3)^2 = 25m^2n^6\),
\(\sqrt{25m^2n^6} = 5mn^3\)Observe que\(2 \div 2 = 1\) y\(6 \div 2 = 3\).
\(-\sqrt{121a^{10}(b-1)^4}\)Buscamos una expresión cuya plaza es\(121a^{10}(b-1)^4\). Desde
\ (\ begin {array} {Flushleft}
\ left [11 a^ {5} (b-1) ^ {2}\ derecha] ^ {2} &= 121a^ {10} (b-1) ^4,\
\\ sqrt {121a^ {10} (b-1) ^4} &= 1a^5 (b-1) ^2\
\ text {Entonces,} -\ sqrt {121a^ {10} (b-1) ^4} &= -11a^5 (b-1) ^2 &\ text {Observe que} 10\ div 2 = 5\ texto {y} 4\ div 2 = 2
\ end {array}\)
Set de Práctica D
Simplifica cada expresión eliminando el signo radical. Supongamos que cada variable es no negativa.
\(\sqrt{y^8}\)
- Contestar
-
\(y^4\)
\(\sqrt{16a^4}\)
- Contestar
-
\(4a^2\)
\(\sqrt{49x^4y^6}\)
- Contestar
-
\(7x^2y^3\)
\(-\sqrt{100x^8y^{12}z^2}\)
- Contestar
-
\(-10x^4y^6z\)
\(-\sqrt{36(a+5)^4}\)
- Contestar
-
\(-6a(a+5)^2\)
\(\sqrt{225w^4(z^2-1)^2}\)
- Contestar
-
\(15w^2(z^2 - 1)\)
\(\sqrt{0.25y^6z^{14}}\)
- Contestar
-
\(0.5y^3z^7\)
\(\sqrt{x^{2n}}\), donde\(n\) es un número natural
- Contestar
-
\(x^n\)
\(\sqrt{x^{4n}}\), donde\(n\) es un número natural.
- Contestar
-
\(x^{2n}\)
Ejercicios
¿Cuántas raíces cuadradas tiene cada número real positivo?
- Contestar
-
dos
El símbolo\(\sqrt{}\) representa qué raíz cuadrada de un número?
El símbolo\(-\sqrt{}\) representa qué raíz cuadrada de un número?
- Contestar
-
secundaria
Para los siguientes problemas, encuentra las dos raíces cuadradas del número dado.
64
81
- Contestar
-
9 y −9
25
121
- Contestar
-
11 y −11
144
225
- Contestar
-
15 y −15
10,000
\(\dfrac{1}{16}\)
- Contestar
-
\(\dfrac{1}{4}\)y\(-\dfrac{1}{4}\)
\(\dfrac{1}{49}\)
\(\dfrac{25}{36}\)
- Contestar
-
\(\dfrac{5}{6}\)y\(-\dfrac{5}{6}\)
\(\dfrac{121}{225}\)
\(0.04\)
- Contestar
-
\(0.2\)y\(-0.2\)
\(0.16\)
\(1.21\)
- Contestar
-
\(1.1\)y\(−1.1\)
Para los siguientes problemas, evalúe cada expresión. Si la expresión no representa un número real, escriba “no un número real”.
\(\sqrt{49}\)
\(\sqrt{64}\)
- Contestar
-
\(8\)
\(-\sqrt{36}\)
\(-\sqrt{100}\)
- Contestar
-
\(-10\)
\(-\sqrt{169}\)
\(-\sqrt{\dfrac{36}{81}}\)
- Contestar
-
\(\dfrac{2}{3}\)
\(-\sqrt{\dfrac{121}{169}}\)
\(\sqrt{-225}\)
- Contestar
-
no es un número real
\(\sqrt{-36}\)
\(-\sqrt{-1}\)
- Contestar
-
no es un número real
\(-\sqrt{-5}\)
\(-(-\sqrt{9})\)
- Contestar
-
\(3\)
\(-(-\sqrt{0.81})\)
Para los siguientes problemas, escriba las restricciones adecuadas que se deben colocar en la variable para que la expresión represente un número real.
\(\sqrt{y + 10}\)
- Contestar
-
\(y≥−10\)
\(\sqrt{x + 4}\)
\(\sqrt{a - 16}\)
- Contestar
-
\(a≥16\)
\(\sqrt{h - 11}\)
\(\sqrt{2k - 1}\)
- Contestar
-
\(k \ge \dfrac{1}{2}\)
\(\sqrt{7x + 8}\)
\(\sqrt{-2x - 8}\)
- Contestar
-
\(x≤−4\)
\(\sqrt{-5y + 15}\)
Para los siguientes problemas, simplifique cada expresión eliminando el signo radical.
\(\sqrt{m^6}\)
- Contestar
-
\(m^3\)
\(\sqrt{k^{10}}\)
\(\sqrt{a^8}\)
- Contestar
-
\(a^4\)
\(\sqrt{h^{16}}\)
\(\sqrt{x^4y^{10}}\)
- Contestar
-
\(x^2y^5\)
\(\sqrt{a^6b^{20}}\)
\(\sqrt{a^4b^6}\)
- Contestar
-
\(a^2b^3\)
\(\sqrt{x^8y^{14}}\)
\(\sqrt{81a^2b^2}\)
- Contestar
-
\(9ab\)
\(\sqrt{49x^6y^4}\)
\(\sqrt{100m^8n^2}\)
- Contestar
-
\(10m^4n\)
\(\sqrt{225p^{14}r^{16}}\)
\(\sqrt{36x^{22}y^{44}}\)
- Contestar
-
\(6x^{11}y^{22}\)
\(\sqrt{169w^4z^6(m-1)^2}\)
\(\sqrt{25x^{12}(y-1)^4}\)
- Contestar
-
\(5x^6(y-1)^2\)
\(\sqrt{64a^{10}(a+4)^{14}}\)
\(\sqrt{9m^6n^4(m + n)^{18}}\)
- Contestar
-
\(3m^3n^2(m + n)^9\)
\(\sqrt{25m^{26}n^{42}r^{66}s^{84}}\)
\(\sqrt{(f-2)^2(g+6)^4}\)
- Contestar
-
\((f-2)(g+6)^4\)
\(\sqrt{(2c - 3)^6 + (5c + 1)^2}\)
\(-\sqrt{64r^4s^{22}}\)
- Contestar
-
\(-8r^2s^{11}\)
\(-\sqrt{121a^6(a-4)^8}\)
\(-[-\sqrt{(w+6)^2}]\)
- Contestar
-
\(w + 6\)
\(-[-\sqrt{4a^2b^2(c^2 + 8)^2}]\)
\(\sqrt{1.21h^4k^4}\)
- Contestar
-
\(1.1h^2k^2\)
\(\sqrt{2.25m^6p^6}\)
\(-\sqrt{\dfrac{169a^2b^4c^6}{196x^4y^6z^8}}\)
- Contestar
-
\(-\dfrac{12ab^2c^3}{14x^2y^3z^4}\)
\(-[\sqrt{\dfrac{81y^4(z-1)^2}{225x^8z^4w^6}}]\)
Ejercicios para la revisión
Encuentra el cociente. \(\dfrac{x^2 - 1}{4x^2 - 1} \div \dfrac{x-1}{2x + 1}\)
- Contestar
-
\(\dfrac{x+1}{2x-1}\)
Encuentra la suma. \(\dfrac{1}{x+1} + \dfrac{3}{x+1} + \dfrac{2}{x^2 - 1}\)
Resuelve la ecuación, si es posible:\(\dfrac{1}{x-2} = \dfrac{3}{x^2 - x - 2} - \dfrac{3}{x+1}\)
- Contestar
-
Ninguna solución;\(x=2\) está excluida.
Realizar la división:\(\dfrac{15x^3 - 5x^2 + 10x}{5x}\)
Realizar la división:\(\dfrac{x^3 - 5x^2 + 13x - 21}{x-3}\)
- Contestar
-
\(x^2 - 2x + 7\)


