10.5: Resolver ecuaciones cuadráticas usando el método de completar el cuadrado
- Page ID
- 112101
La lógica detrás del método
Supongamos que deseamos resolver la ecuación cuadrática\(x^2 - 3x - 1 = 0\). Como la ecuación no es de la forma\(x^2 = K\), no podemos utilizar la extracción de raíces. A continuación, intentamos factorizar, pero después de algunos ensayos vemos que no\(x^2 - 3x - 1\) es factorizable. Necesitamos otro método para resolver ecuaciones cuadráticas.
El método que estudiaremos se basa en trinomios cuadrados perfectos y extracción de raíces. El método se llama resolver ecuaciones cuadráticas completando el cuadrado. Considera la ecuación
\[x^2 + 6x + 5 = 0.\]
Esta ecuación cuadrática podría resolverse factorizando, pero usaremos el método de completar el cuadrado. Vamos a explicar el método en detalle después de que veamos este ejemplo. Primero reescribiremos la ecuación como
\[x^2 + 6x = -5\]
Después, agregaremos\(9\) a cada lado. Obtenemos
\[x^2 + 6x + 9 = -5 + 9\]
Los factores del lado izquierdo como trinomio cuadrado perfecto.
\[(x + 3)^2 = 4\]
Esto lo podemos resolver mediante la extracción de raíces.
\ [\ begin {array} {Flushleft}
x + 3 &=\ pm\ sqrt {4}\\
x + 3 &=\ pm 2\\
x &=\ pm 2 - 3\\
x &= + 2 - 3 &\ texto {y} & x = -2 - 3\\
x &= -1 &\ texto {y} -5
\ end {array}\]
Observe que cuando las raíces son números racionales, la ecuación es factorizable.
La gran pregunta es: “¿Cómo sabíamos sumar 9 a cada lado de la ecuación?” Podemos convertir cualquier trinomio cuadrático que aparezca en una ecuación en un trinomio cuadrado perfecto si sabemos qué número sumar a ambos lados. Podemos determinar ese número en particular observando la siguiente situación:
Considera el cuadrado del binomio y el trinomio cuadrado perfecto resultante
\[(x + p)^2 = x^2 + 2px + p^2\]
Observe que el término constante (el número que estamos buscando) se puede obtener del término lineal\(2px\). Si tomamos la mitad del coeficiente de\(x\),\(\dfrac{20}{2} = p\), y lo cuadramos, obtenemos el término constante\(p^2\). Esto es cierto para cada trinomio cuadrado perfecto con un coeficiente principal\(1\).
En un trinomio cuadrado perfecto con coeficiente principal\(1\), el término constante es el cuadrado de la mitad del coeficiente del término lineal.
Estudia estos ejemplos para ver qué término constante convertirá al binomio dado en un trinomio cuadrado perfecto.
\(x^2 + 6x\). La constante debe ser el cuadrado de la mitad del coeficiente de\(x\). Desde el coeficiente de\(x\) es\(6\), tenemos
\(\dfrac{6}{2} = 3\)y\(3^2 = 9\)
La constante es\(9\).
\[x^2 + 6x + 9 = (x + 3)^2\]
Este es un trinomio cuadrado perfecto.
\(a^2 + 10a\). La constante debe ser el cuadrado de la mitad del coeficiente de\(a\). Desde el coeficiente de\(a\) es\(10\), tenemos
\(\dfrac{10}{2} = 5\)y\(5^2 = 25\).
La constante es\(25\)
\[a^2 + 10a + 25 = (a + 5)^2\]
\(y^2 + 3y\). La constante debe ser el cuadrado de la mitad del coeficiente de\(y\). Desde el coeficiente de\(y\) es\(3\), tenemos
\(\dfrac{3}{2}\)y\((\dfrac{3}{2})^2 = \dfrac{9}{4}\)
La constante es\(\dfrac{9}{4}\).
\[y^2 + 3y + \dfrac{9}{4} = (y + \dfrac{3}{2})^2\]
El Método De Completar La Plaza
Ahora, con estas observaciones, podemos describir el método para completar el cuadrado.
- Escribe la ecuación para que el término constante aparezca en el lado derecho de la ecuación.
- Si el coeficiente principal es diferente de 1, divida cada término de la ecuación por ese coeficiente.
- Tomar la mitad del coeficiente del término lineal, cuadrarlo, luego agregarlo a ambos lados de la ecuación.
- El trinomio de la izquierda es ahora un trinomio cuadrado perfecto y se puede factorizar como\(()^2\). El primer término entre paréntesis es la raíz cuadrada del término cuadrático. El último término entre paréntesis es la mitad del coeficiente del término lineal.
- Resolver esta ecuación por extracción de raíces.
Conjunto de Muestras A
Resuelve las siguientes ecuaciones.
\ (\ begin {array} {Flushleft}
x^2 + 8x - 9 &= 0 &\ text {Agregar} 9\ texto {a ambos lados.} \\
x^2 + 8x &= 9 &\ text {La mitad del coeficiente de} x\ text {es} 4,\ text {y} 4^2\ text {es} 16. \ texto {Agregar} 16\ texto {a ambos lados.}\\
x^2 + 8x + 16 &= 9 + 16\\
x^2 + 8x + 16 &= 25 &\ text {Factor.}\\
(x+4) ^2 &= 25 &\ text {Toma raíces cuadradas.}\\
x + 4 &=\ pm 5\\
x &=\ pm 5 - 4 & +5 - 4 = 4 1, -5 - 4 = -9\\
x &= 1, -9
\ end {array}\)
\ (\ begin {array} {Flushleft}
x^2 - 3x - 1 &= 0 &\ text {Agregar} 1\ texto {a ambos lados.} \\
&&\ text {La mitad del coeficiente de} x\ text {es}\ dfrac {-3} {2}. \\
x^2 - 3x &= 1 &\ text {Cuadrarlo:} (\ dfrac {-3} {2}) ^2 =\ dfrac {9} {4}. \ texto {Agregar}\ dfrac {9} {4}\ texto {a cada lado.} \\
x^2 - 3x +\ dfrac {9} {4} &= 1 +\ dfrac {9} {4}\
x^2 - 3x +\ dfrac {9} {4} &=\ dfrac {13} {4} &\ text {Factor. Observe que dado que el signo del término medio del trinomio es “-”, su forma factorizada tiene un signo de “-”.} \\
(x -\ dfrac {3} {2}) ^2 &=\ dfrac {13} {4} &\ text {Ahora toma raíces cuadradas}\\
x -\ dfrac {3} {2} &=\ pm\ sqrt {\ dfrac {13} {4}}\\
x -\ dfrac {3} {2} &=\ pm\ sqrt\ dfrac {13} {2}}\\
x &=\ pm\ dfrac {\ sqrt {13}} {2} +\ dfrac {3} {2}\\
x &=\ dfrac {\ pm\ sqrt {13} + 3} {2}\\
x &=\ dfrac {3\ pm\ sqrt {13}} {2}
\ end {array}\)
\ (\ begin {array} {Flushleft}
3a^2 - 36a - 39 &= 0 &\ text {Agregar} 39\ texto {a ambos lados.} \\
3a^2 - 36a &= 39 &\ text {El coeficiente principal es} 3\ text {y necesitamos que sea} 1. \ text {Divide cada término por} 3\ text {. La mitad del coeficiente de} a\ text {es} -6\\
a^2 - 12a &= 13 &\ text {Cuadrarlo:} (-6) ^2 = 36\ text {Agregar} 36\ text {a cada lado.}\\
a^2 - 12a + 36 &= 13 + 36\
a^2 - 12a + 36 &= 49\
(a-6) ^2 &= 49 &\ text {Factor.}\\
a - 6 &=\ pm 7\\
a &=\ pm 7 + 6 & +7 + 6 = 13, -7 + 6 = -1
\ end {array}\)
\(a = 13, -1\).
\ (\ begin {array} {Flushleft}
2x^2 + x + 4 &= 0\\
2x^2 + x &= -4\\
x^2 +\ dfrac {1} {2} x &= -2\
x^2 +\ dfrac {1} {2} x + (\ dfrac {1} {4}) ^2 &= -2 + (\ dfrac {1}} {4}) ^2
\ end {array}\)
\((x + \dfrac{1}{4})^2 = -2 + \dfrac{1}{16} = \dfrac{-32}{16} + \dfrac{1}{16} = \dfrac{-31}{16}\)
Como sabemos que el cuadrado de cualquier número es positivo, esta ecuación no tiene solución de número real.
Problema de la calculadora:
Resolver\(7a^2 - 5a - 1 = 0\). Redondear cada solución a la décima más cercana.
\ (\ begin {array} {Flushleft}
7a^2 - 5a - 1 &= 0\\
7a^2 - 5a &= 1\\
a^2 -\ dfrac {5} {7} a &=\ dfrac {1} {7}\\
a^2 -\ dfrac {5} {7} a + (\ dfrac {5} {14}) ^2 &=\ dfrac {1} {7} + (\ dfrac {5} {14}) ^2\\
(a -\ dfrac {5} {14}) ^2 &=\ dfrac {1} {7} +\ dfrac {25} {196} &=\ dfrac {28} {196} +\ dfrac {25} {196} =\ dfrac {53} {196}\
a -\ dfrac {5} {14} &=\ pm\ sqrt {53} {196}} &=\ pm\ dfrac {53} {14}
\ end {array}\)
\(a = \dfrac{5}{14} \pm \dfrac{\sqrt{53}}{14} = \dfrac{5 \pm \sqrt{53}}{14}\)
Redondeando a décimas, obtenemos\(a \approx -0.2\). Así,\(a \approx 0.9\) y\(-0.2\) a la décima más cercana.
Conjunto de práctica A
Resuelve cada una de las siguientes ecuaciones cuadráticas utilizando el método de completar el cuadrado.
\(x^2 - 2x - 48 = 0\)
- Contestar
-
\(x=−6, 8\)
\(x^2 + 3x - 5 = 0\)
- Contestar
-
\(x = \dfrac{-3 \pm \sqrt{29}}{2}\)
\(4m^2 + 5m = -1\)
- Contestar
-
\(m = \dfrac{-1}{4}, -1\)
\(5y^2 - 2y - 4 = 0\)
- Contestar
-
\(y = \dfrac{1 \pm \sqrt{21}}{5}\)
Problema de la calculadora:
Resolver\(3x^2 - x - 1= 0\). Redondear cada solución a la décima más cercana.
- Contestar
-
\(x = 0.8, -0.4\)
Ejercicios
Para los siguientes problemas, resuelve las ecuaciones completando el cuadrado.
\(x^2 +2x - 8 = 0\)
- Contestar
-
\(x=−4, 2\)
\(y^2 - 5y - 6 = 0\)
\(a^2 + 7a + 12 = 0\)
- Contestar
-
\(a=−3, −4\)
\(x^2 - 10x + 16 = 0\)
\(y^2 - 2y - 24 = 0\)
- Contestar
-
\(y = -4, 6\)
\(a^2 + 2a - 35 = 0\)
\(x^2 + 2x + 5 = 0\)
- Contestar
-
Sin solución de números reales.
\(x^2 - 6x + 1 = 0\)
\(x^2 + 4x + 4 = 0\)
- Contestar
-
\(x=−2\)
\(a^2 + 4a + 7 = 0\)
\(b^2 + 5b - 3 = 0\)
- Contestar
-
\(b = \dfrac{-5 \pm \sqrt{37}}{2}\)
\(b^2 - 6b = 72\)
\(a^2 + 10a - 9 = 0\)
- Contestar
-
\(a = -5 \pm \sqrt{34}\)
\(a^2 - 2a - 3 = 0\)
\(x^2 - 10x = 0\)
- Contestar
-
\(x=10, 0\)
\(y^2 - 8y = 0\)
\(a^2 - 6a = 0\)
- Contestar
-
\(a = 6, 0\)
\(b^2 + 6b = 0\)
\(-x^2 - 14x = 13\)
- Contestar
-
\(x=−13, −1\)
\(-x^2 +8x = -84\)
\(2a^2 + 2a - 1 = 0\)
- Contestar
-
\(a = \dfrac{-1 \pm \sqrt{3}}{2}\)
\(4b^2 - 8b = 16\)
\(9x^2 + 12x - 5 = 0\)
- Contestar
-
\(x = \dfrac{1}{3}, -\dfrac{5}{3}\)
\(16y^2 - 8y - 3 = 0\)
\(2x^2 + 5x - 4 = 0\)
- Contestar
-
\(x = \dfrac{-5 \pm \sqrt{57}}{4}\)
\(3a^2 + 2a - 24 = 0\)
\(x^2 + 2x + 8 = 0\)
- Contestar
-
Sin solución de números reales.
\(y^2 - 3y + 10 = 0\)
\(7a^2 + 3a - 1 = 0\)
- Contestar
-
\(a = \dfrac{-3 \pm \sqrt{37}}{14}\)
Problemas con la calculadora
Para los siguientes problemas, redondear cada solución a la centésima más cercana.
\(5m^2 - 2m - 6 = 0\)
\(3y^2 + 5y = 7\)
- Contestar
-
\(y=0.91, −2.57\)
\(1.8x^2 + 2.3x - 4.1 = 0\)
\(0.04a^2 - 0.03a + 0.02 = 0\)
- Contestar
-
Sin solución de números reales.
Ejercicios para revisión
Facturar\(12ax - 6bx + 20ay - 10by\) por agrupación.
Graficar la desigualdad compuesta\(-6 \le -2x + 2 < -4\)

- Contestar
-
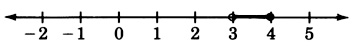
Encuentra la ecuación de la línea que pasa por los puntos\((1, -2)\) y\((0, 4)\)
Encuentra el producto:\(\dfrac{x^2 - 4x - 12}{x^2 - 2x - 8} \cdot \dfrac{x^2 - 3x - 4}{x^2 - 3x - 18}\)
- Contestar
-
\(\dfrac{x+1}{x+3}\)
Utilizar el método de extracción de raíces para resolver\((x-2)^2 = 25\)


